下载文档原格式
DYNAFORM材料参数说明18#材料模型：（幂指数塑性材料模型）没有考虑材料的厚向异性，只在一些简单的各向同性材料中应用。
MASS DENSITY——质量密度；YOUNG MODULUS——杨氏模量；POISSONS RATIO——泊松比；STRENGTH COEFF（K）——强度系数；HARDENING EXPONENT（N）——强化系数，也就是人们常说的硬化指数；STRAIN RATE PARAM （C）——Couper—symonds应变率系数C；STRAIN RATE PARAM （P）——Couper—symonds应变率系数P；INITIAL YIELD STRESS——初始屈服应力；FORMULATION——用公式表示。
24#材料模型：（分段线性材料模型）主要用于一些各向同性材料的冲压分析中。
MASS DENSITY——质量密度；YOUNG MODULUS——杨氏模量；POISSONS RATIO——泊松比；YIELD STRESS——屈服应力；TANGENT MODULUS——切变模量；FAILURE PL。
STRAIN——材料失效时的等效塑性应变；STEP SIZE FOR EL. DEL——段数；STRAIN RATE PARAM （C）——Couper—symonds应变率系数C；STRAIN RATE PARAM （P）——Couper—symonds应变率系数P；36#材料模型（Barlat’s-3 Parameter Plasticity Model）——3参数Barlat材料模型这种材料模型适用于任何薄板金属成形分析，特别是对象铝合金必须用次模型分析。
使用此模型一般输入以下参数：MASS DENSITY（质量密度）；YOUNG MODULUS（杨氏模量）；POISSONS RATIO（泊松比）；EXPONENT FACE M（Barlat指数m）；LANKFORD PARAM R0（各向异性参数r0）；LANKFORD PARAM R45（各向异性参数r45）；LANKFORD PARAM R90（各向异性参数r90）；HARDENING RULE（EXPON．）（硬化规律：对于线性硬化模型，HR=1；对于幂指数硬化模型，HR=3；对于分段线性硬化模型，不需要输入HR）；ＭATEIAL PARAM P1（K）和ＭATEIAL PARAM P2（N）是材料参数：⑴对于线性硬化模型：P1=切线模量=tg(α); P2=屈服应力σs；⑵对于幂指数硬化模型：P1=k（强化系数）；P2=n（强化指数）；⑶对于分段线性硬化模型，不需要输入：HR，P1，P2，E0，SPI等参数的值。
ls-dyna中常用弹塑性材料卡片的设置方法及要点在进行冲击动力学仿真计算时，如碰撞、跌落、冲击等工况，金属材料或其他塑性材料的变形不再是小变形，此时需要设置成弹塑性材料，方能正确地计算结构的应力、应变结果。
本文这里不考虑金属材料在冲击变形过程中的率效应、硬化效应、温度效应中的参数设置，因为在大多数企业里，通常不会做这方面的材料性能参数研究。
那么，我们经常用到的弹塑性材料卡片也就是MAT03、MAT24。
MAT03可视为双线性弹塑性模型，MAT24和MAT03类似，其还可以输入试验数据（真实应力-塑性应变，如果能找到的话），二者都自带材料失效模式（通过失效应变判定）。
MAT03卡片：
关键设置参数：切线模量。
因为没有试验数据，故需要根据屈服强度、屈服强度对应的应变、破坏强度和断裂伸长率(工程应变)来进行简单的估算。
失效准则：通过失效应变判定。
根据需要设置，一般以最大拉伸应力开始下降时对应的应变，即材料发生颈缩时。
注：这里提供的双线性应力应变曲线，原则上只能模拟材料在准静态下材料的动态变形行为。
因为一般金属等塑性材料在承受中、高应变率的冲击时，材料性能将得到强化效应，而塑性会减小。
MAT24卡片：
1.可以直接当MAT03来使用，不用输入试验数据。
2.当有试验数据时，不需要设置切线模量了。
输入的第一列数据，塑性应变为
0时对应的真实应力，即为材料的屈服强度（弹性极限强度）。
弹性模量的输入应以实际测得的值为准（可能与常用的推荐值有些差异）。
LS-DYNA是一款广泛使用的显式动力学有限元分析软件，它被用于解决复杂的结构和材料动力学问题。
在LS-DYNA中，状态方程用于描述材料在不同应变、应力和温度条件下的性能变化。
LS-DYNA支持多种材料模型，每个模型都可以使用不同的状态方程。
以下是LS-DYNA 中常见的一些状态方程：
1. 线性弹性: 线性弹性是最简单的状态方程，它假设材料在弹性行为范围内的应力-应变关系服从胡克定律。
常见的线性弹性状态方程包括各向同性弹性和各向异性弹性。
2. 现行弹性: 现行弹性是一种常见的状态方程，广泛用于描述金属材料的弹塑性行为。
常见的现行弹性模型包括von Mises屈服准则、Tresca屈服准则等。
3. 可调组分模型: 可调组分模型是一种材料模型，用于描述复杂的动力学行为，如弹塑性、损伤、断裂等。
这些模型通常使用包含一些可调参数的状态方程，以逼近实验数据。
例如，Johnson-Cook模型、Cockcroft-Latham模型等。
4. 温度效应: 材料的温度对其性能有明显影响。
LS-DYNA中的状态方程可以包括考虑温度效应的材料参数。
常见的温度效应模型包括线性温度函数、非线性温度函数等。
dyna高分子聚合物材料本构模型
dyna高分子聚合物材料本构模型是一种用于描述这类材料力学性质的数学模型。
本构模型的目的是通过数学形式化描述材料的应力-应
变行为，从而能够预测其在不同外界加载条件下的力学响应。
在dyna高分子聚合物材料中，通常采用弹性本构模型来描述其
力学性质。
弹性本构模型假设材料在外界加载后，能够在加载结束后
完全恢复其初始形态，且应力-应变关系是线性的。
这意味着材料的应
力是其应变的线性函数，并且与加载的时间无关。
dyna高分子聚合物材料的弹性本构模型可以用应力-应变关系的
张量表示。
其中的张量元素表示在某一方向上的应力与应变之间的关系。
根据材料的各向同性性质，张量的元素可以简化为标量形式。
弹性本构模型还可以进一步拓展，以考虑非线性效应，如应力松弛、刚度变化等。
这些非线性本构模型通常通过材料实验数据来确定，并使用合适的数学函数来刻画材料的非线性行为。
总之，dyna高分子聚合物材料本构模型是一种数学模型，用于描述这类材料的力学性质。
它通过数学形式化描述材料的应力-应变行为，并能够预测其在外界加载条件下的力学响应。
了解这些本构模型可以
帮助研究人员更好地理解和设计dyna高分子聚合物材料的力学性能。
文章主题：深入探讨lsdyna混凝土本构模型参数1.引言在工程领域中，混凝土是一种常见的建筑材料，其在工程结构中起着至关重要的作用。
在进行工程仿真计算时，为了准确地模拟混凝土材料的力学行为，需要采用适当的本构模型以描述材料的力学性能。
lsdyna作为一种常用的仿真软件，其混凝土本构模型参数的选择对仿真计算结果的准确性和可靠性至关重要。
本文将深入探讨lsdyna混凝土本构模型参数的相关知识，以便读者能够更好地理解和应用这些参数。
2.混凝土本构模型参数的选择混凝土在lsdyna中常用的本构模型包括弹塑性本构模型、本构模型等。
在选择适当的本构模型参数时，我们需要考虑混凝土的材料性质、加载条件、模拟精度等方面的因素。
其中，本构模型参数的选择是至关重要的一步。
具体包括但不限于杨氏模量、泊松比、屈服强度、极限强度、变形能力等参数的合理选取。
3.深入分析lsdyna混凝土本构模型参数的影响混凝土本构模型参数的不同选择会直接影响到仿真计算结果的准确性和可靠性。
杨氏模量和泊松比是混凝土本构模型参数中至关重要的两个参数，它们直接影响到混凝土的弹性模量和材料的变形情况。
屈服强度和极限强度是表征混凝土抗压性能的重要参数，它们会影响到混凝土在受力过程中的破坏形式和破坏时间。
变形能力是混凝土本构模型参数中比较难以确定的参数，但其选择对于仿真计算结果的准确性同样有着重要的影响。
4.个人观点和理解在选择lsdyna混凝土本构模型参数时，我个人认为需要充分考虑混凝土的实际工程应用情况，尽可能地采用真实的材料性能参数。
针对不同的工程结构和不同的加载条件，需要根据实际情况进行参数的合理选择和调整。
总体来说，lsdyna混凝土本构模型参数的选择需要结合理论和实际，并在仿真计算中进行验证和修正，以确保计算结果的准确性和可靠性。
5.总结lsdyna混凝土本构模型参数的选择对于工程仿真计算至关重要。
深入分析其影响，充分考虑混凝土材料的特性和工程应用情况，合理选择和调整参数，才能得到准确可靠的仿真计算结果。
第一章Dyna中已有的关于金属成形的材料模型$1.1 *MAT_003(*MAT_PLASTIC_KINEMATIC)这个模型适合模拟等向和运动强化塑性，有选项可以考虑率效应。
适合于：梁（Hughes-Liu），壳和实体单元。
$1.2 *MAT_012(*MAT_ISOTROPIC_ELASTIC_PLASTIC)这是一个低耗等向塑性模型，适合于三维实体。
对于平面应力壳单元计算中，当应力状态超过屈服表面时，一步radial return approach被采用来修正Cauchy应力张量。
这种方法导致不准确的壳厚度更新和不准确的屈服后应力。
这是dyna平面应力分析中唯一不缺省采用迭代方法的模型。
$1.3 *MAT_018(*MAT_POWER_LAW_PLASTICITY)这是一个考虑率效应的等向塑性模型，采用指数强化。
$1.4 *MAT_024(*MAT_PIECEWISE_LINEAR_PLASTICITY)可以定义任意应力应变曲线的弹塑性材料模型。
$1.5 *MAT_033(*MAT_BARLAT_ANISOTROPIC_PLASTICITY)该模型由Barlat, Lege, and Brem[1991]开发，用来模拟成形过程中的各向异性材料行为。
这个模型的有限元执行由Chung and Shah[1992]详细描述。
它基于六参数模型，适合于三维连续问题。
Barlat, F., D.J. Lege, and J.C. Brem, "A Six-Component Yield Function for Anisotropic Materials,", Int. J. of Plasticity, 7, 693-712, (1991).Chung, K. and K. Shah, "Finite Element Simulation of Sheet Metal Forming for Planar Anisotropic Metals," Int. J. of Plasticity, 8, 453-476, (1992).$1.6 MAT_033_96(*MAT_BARLAT_YLD96)这个模型是由Barlat等人[1997]提出用来模拟成形过程中的各向异性材料行为（尤其适用于铝合金）。
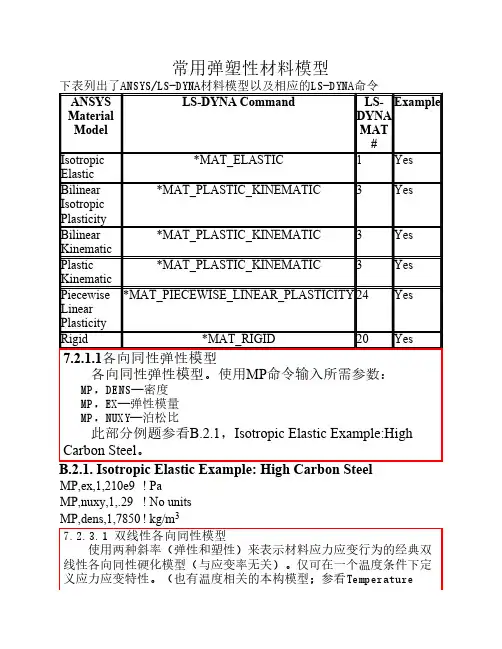
常用弹塑性材料模型MP,ex,1,210e9! PaMP,nuxy,1,.29! No unitsMP,dens,1,7850! kg/m37.2.3.1 双线性各向同性模型使用两种斜率（弹性和塑性）来表示材料应力应变行为的经典双线性各向同性硬化模型（与应变率无关）。
仅可在一个温度条件下定义应力应变特性。
（也有温度相关的本构模型；参看TemperatureDependent Bilinear Isotropic Model）。
用MP命令输入弹性模量（Exx），泊松比（NUXY）和密度（DENS），程序用EX和NUXY值计算体积模量（K）。
用TB和TBDATA命令的1和2项输入屈服强度和切线模量：TB，BISOTBDATA，1，（屈服应力）TBDATA，2，（切线模量）例题参看B.2.7,Bilinear Isotropic Plasticity Example：Nickel Alloy。
B.2.7. Bilinear Isotropic Plasticity Example: Nickel Alloy MP,ex,1,180e9! PaMP,nuxy,1,.31! No unitsMP,dens,1,8490! kg/m3TB,BISO,1TBDATA,1,900e6! Yield stress (Pa)TBDATA,2,445e6! Tangent modulus (Pa)7.2.3.5双线性随动模型（与应变率无关）经典的双线性随动硬化模型，用两个斜率（弹性和塑性）来表示材料的应力应变特性。
用MP命令输入弹性模量（Exx），密度（DENS）和泊松比（NUXY）。
可以用TB，BKIN和TBDATA命令中的1-2项输入屈服强度和切线模量：TB，BKINTBDATA，1，（屈服应力）TBDATA，2，（切线模量）例题参看B.2.10，Bilinear Kinematic Plasticity Example ：Titanium Alloy。
