第十七章-弹塑性分析详解
- 格式:ppt
- 大小:1.30 MB
- 文档页数:28





弹塑性分析什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说当其应力低于比例极限时,应力一应变关系是线性的。
另外,大多数材料在其应力低于屈服点时,表现为弹性行为,也就是说,当移走载荷时,其应变也完全消失。
由于屈服点和比例极限相差很小,因此在ANSYS程序中,假定它们相同。
在应力一应变的曲线中,低于屈服点的叫作弹性部分,超过屈服点的叫作塑性部分,也叫作应变强化部分。
塑性分析中考虑了塑性区域的材料特性。
路径相关性:即然塑性是不可恢复的,那么这种问题的就与加载历史有关,这类非线性问题叫作与路径相关的或非保守的非线性。
路径相关性是指对一种给定的边界条件,可能有多个正确的解一内部的应力,应变分布一存在,为了得到真正正确的结果,我们必须按照系统真正经历的加载过程加载。
率相关性:塑性应变的大小可能是加载速度快慢的函数,如果塑性应变的大小与时间有关,这种塑性叫作率无关性塑性,相反,与应变率有关的性叫作率相关的塑性。
大多的材料都有某种程度上的率相关性,但在大多数静力分析所经历的应变率范围,两者的应力一应变曲线差别不大,所以在一般的分析中,我们变为是与率无关的。
工程应力,应变与真实的应力、应变:塑性材料的数据一般以拉伸的应力一应变曲线形式给出。
材料数据可能是工程应力()与工程应变(),也可能是真实应力(P/A)与真实应变()。
大应变的塑性分析一般采用真实的应力,应变数据而小应变分析一般采用工程的应力、应变数据。
什么时候激活塑性:当材料中的应力超过屈服点时,塑性被激活(也就是说,有塑性应变发生)。
而屈服应力本身可能是下列某个参数的函数。
*温度・应变率*以前的应变历史*侧限压力・其它参数塑性理论介绍在这一章中,我们将依次介绍塑性的三个主要方面:•屈服准则•流动准则*强化准则屈服准则:对单向受拉试件,我们可以通过简单的比较轴向应力与材料的屈服应力来决定是否有塑性变形发生,然而,对于一般的应力状态,是否到达屈服点并不是明显的。
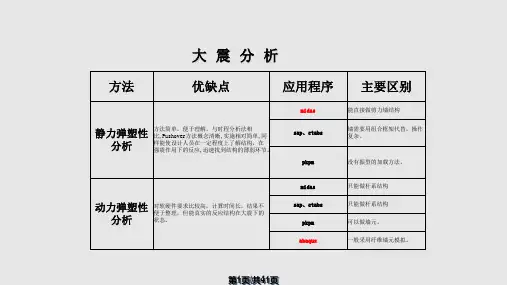





结构静力弹塑性分析的原理和计算实例一、本文概述结构静力弹塑性分析是一种重要的工程分析方法,用于评估结构在静力作用下的弹塑性行为。
该方法结合了弹性力学、塑性力学和有限元分析技术,能够有效地预测结构在静力加载过程中的变形、应力分布以及破坏模式。
本文将对结构静力弹塑性分析的基本原理进行详细介绍,并通过计算实例来展示其在实际工程中的应用。
通过本文的阅读,读者可以深入了解结构静力弹塑性分析的基本概念、分析流程和方法,掌握其在工程实践中的应用技巧,为解决实际工程问题提供有力支持。
二、弹塑性理论基础弹塑性分析是结构力学的一个重要分支,它主要关注材料在受力过程中同时发生弹性变形和塑性变形的情况。
在弹塑性分析中,材料的应力-应变关系不再是线性的,而是呈现出非线性特性。
当材料受到的应力超过其弹性极限时,材料将发生塑性变形,这种变形在卸载后不能完全恢复,从而导致结构的永久变形。
弹塑性分析的理论基础主要包括塑性力学、塑性理论和弹塑性本构关系。
塑性力学主要研究塑性变形的产生、发展和终止的规律,它涉及到塑性流动、塑性硬化和塑性屈服等概念。
塑性理论则通过引入屈服函数、硬化法则和流动法则等,描述了材料在塑性变形过程中的应力-应变关系。
弹塑性本构关系则综合考虑了材料的弹性和塑性变形行为,建立了应力、应变和应变率之间的关系。
在结构静力弹塑性分析中,通常需要先确定材料的弹塑性本构模型,然后结合结构的边界条件和受力情况,建立结构的弹塑性平衡方程。
通过求解这个平衡方程,可以得到结构在静力作用下的弹塑性变形和应力分布。
弹塑性分析在结构工程中有着广泛的应用,特别是在评估结构的承载能力、变形性能和抗震性能等方面。
通过弹塑性分析,可以更加准确地预测结构在极端荷载作用下的响应,为结构设计和加固提供科学依据。
以上即为弹塑性理论基础的主要内容,它为我们提供了分析结构在弹塑性阶段行为的理论框架和工具。
在接下来的计算实例中,我们将具体展示如何应用这些理论和方法进行结构静力弹塑性分析。
弹塑性分析实例1.弹塑性分析中的主要问题ABAQUS提供了多种材料的本构关系和失效准则模型弹塑性变形行为:Abaqu默认的采用屈服面来定义各项同性屈服金属材料的弹塑性行为:(四个阶段)曲线:弹性阶段:p,应力应变服从胡克定律:Epe,不再是线性关系,卸载后变形完全消失,仍属于弹性变形屈服阶段:屈服阶段表现为显著的塑性变形,此阶段应力基本不变,应变不断增加,屈服现象的出现于最大切应力有关系,屈服极限为强化阶段:材料恢复抵抗变形的能力,使它继续变形必须增加拉力,强度极限为b局部变形阶段:b后,在试样的某一局部范围内,横向尺寸突然急剧减小,形成缩颈现象卸载定律,冷作硬化(比例极限得到提高,退火后可消除)伸长率5%,称为脆性材料;5%,称为塑性材料强度极限b是衡量脆性材料的唯一指标,脆性材料主要用作受压杆件,破坏处发生在与轴线成45的斜截面上,而塑性材料主要用作受拉杆件。
应以应力和名义应变:(以变形前的界面尺寸为基础)nomFA0nomllo真实应力和真实应变与名义量的关系:truenom(1nom)trueln(1nom)真实应变是由弹性应变和塑性应变组成的,定义塑性材料时,需用到塑性应变,其表达式为:pltruee1trueAbaqu分析结果中对应的变量:真实应力:S,MietrueE真实应变:对几何非线性问题,输出的是对数应变LE;几何线性问题,输出的是总应变E塑性应变:等效塑性应变PEEQ,塑性应变量PEMAG,塑性应变分量PE弹性应变:EE名义应变:NE在abaqutandard中无法模拟构建塑性变形过大而破坏的过程理想塑性:应力不变,应变持续增加;应尽可能的使材料的最大真实应力和塑性应变大于模型可能出现的应力应变值解决弹塑性分析中的收敛问题:在弹塑性材料商施加载荷时,如果此载荷会造成很大的局部变形(使用点载荷时尤其容易出现此问题),可能造成收敛问题。
解决方法有四种:1.使材料的最大真实应力和塑性应变大于模型可能出现的应力应变值2.如果对出现很大苏醒变形的部件不关心其准确的应力和塑性变形,可将其设置为线弹性材料3.尽量不要施加点载荷,而是根据实际情况来使用面载荷或线载荷4.为载荷作用点附近的几个节点建立刚性约束,施加耦合约束,使几个节点共同承担点载荷Abaqu中的体积自锁问题?2.带孔平板的弹塑性分析通过查看PEEQ(等效塑性变形),判断材料是否发生塑性变形。
弹塑性力学讲义弹塑性力学1 弹塑性的概念所谓弹塑性指的是物体在外力作用下发生变形而外力除去后变形不能完全恢复的性质。
变形中可回复的部分称为弹性变形,变形中不可回复的部分称为塑性变形。
塑性变形总是在外力的作用超过一定的限度后出现。
2 简单拉压状态下金属材料弹塑性行为及其数学模型(1)理想塑性材料的弹塑性行为σs主要特点:屈服后加载,表现出一种流动变形现象,材料失去进一步承载的能力;屈服后卸载,应力应变增量大致与弹性变形段相同。
卸载至零后再次加载,应力应变关系相当于原应力应变关系曲线在应变轴方向作了一个平移,平移量为残余塑性应变。
数学表达:Eε(0 ε εs)σ σ(ε)σ(ε ε)s s Eε( εs ε 0)σ σ(ε)(ε εs) σs(2)线性强化材料的弹塑性行为σσs主要特点:屈服后加载,材料仍有进一步承载的能力,但应力应变增量的比例较弹性段小;屈服后卸载,应力应变增量大致与弹性变形段相同。
卸载至零后再次加载,屈服应力为卸载前的应力值(较先前的屈服应力大),应力应变关系相当于原应力应变关系曲线在应变轴方向作了一个平移,平移量为残余塑性应变,同时应力轴伸长。
两种常用的强化模型数学表达:Eε(0 ε εs)σ σ(ε)σ E(ε ε)(ε ε)ss sEε( εs ε 0)σ σ(ε)σs E(ε εs)(ε εs)上述描述弹塑性材料应力应变关系的数学模型称为全量型本构关系。
显然不能代表弹塑性变形规律的全貌。
它描述了单调应力-应变过程。
为了描述弹塑性力学行为的“过程相依”,需要建立增量型本构关系。
记当前应力为σ0,应力增量为dσ,应变增量为dε,分析弹塑性行为可以得出相应的增量变形法则。
理想塑性材料的增量型弹塑性关系(1)由dσ决定dε当σs σ0 σs时,dε dσ/E 当σ0 σs时,dεdλσ0ifdσ 0 dσ/Eifdσ 0dλσ0ifdσ 0当σ0 σs时,dεdσ/Eifdσ 0(2)由dε决定dσ当σs σ0 σs时,dσ Edε0ifdε 0当σ0 σs时,dσEdεifdε 0当σ0 σs时,dσ0ifdε 0 Edεifdε 0例:已经测得某理想弹塑性材料的细杆所经受的轴向应变过程如图所示,试求此杆中的应力过程。