机械制图直角三角形法

直角三角形法在机械制图课程教学中的探讨【摘要】本文探讨了直角三角形法在机械制图课程教学中的重要性及应用。

首先介绍了直角三角形法的基本原理，然后讨论了在机械制图中的具体应用和实践探索。

接着通过实际工程案例分析了直角三角形法的应用，以及对学生学习效果的影响。

结论部分强调了直角三角形法在教学中的重要性，提出了潜在挑战及解决方法，并探讨了未来研究方向。

通过本文的研究，能够帮助教师和学生更好地理解并应用直角三角形法，提高机械制图课程教学的质量和效果，为未来教学和研究提供有益参考。

【关键词】直角三角形法、机械制图课程、教学探讨、实践探索、学习效果、应用案例、重要性、挑战与解决、未来研究方向1. 引言1.1 研究背景研究背景部分将探讨直角三角形法在机械制图中的重要性和应用价值。

在工程设计与制造过程中，直角三角形法可以帮助工程师准确、快速地绘制各种复杂图形，提高工作效率。

而在机械制图教学过程中，合理地引入直角三角形法可以帮助学生理解基本绘图原理，提高他们的绘图技能和空间想象能力，为将来从事工程设计和制造工作奠定坚实的基础。

通过深入研究直角三角形法在机械制图课程中的应用和实践探索，可以更好地指导教师如何有效地传授和运用这一绘图方法，提高学生的学习效果和专业素养。

本研究旨在探讨直角三角形法在机械制图课程教学中的重要性和实际应用，为提高教学质量和学生绘图能力提供理论支持和实践指导。

1.2 研究目的研究目的是为了探讨直角三角形法在机械制图课程教学中的应用效果，分析该方法对学生学习的实际帮助和影响，以期提出更有效的教学策略和方法。

通过深入研究直角三角形法的基本原理和在实际工程中的应用案例，探讨其在机械制图课程中的实践探索，希望从中总结出对学生学习效果有积极影响的因素，并为今后的教学工作提供指导和借鉴。

通过研究直角三角形法在实际工程中的应用案例，可以更好地理解这一方法的实用性和重要性，为教学内容的更新和完善提供参考。

最终目的是为了提高学生对机械制图课程的学习兴趣和能力，促进他们将所学知识运用于实际工程中，提高专业技能和竞争力。

机械制图：直角三角形法机械制图是机械工程中非常重要的一部分，是用于表达和传递机械工程设计信息的工具。

在机械制图中，直角三角形法是常用的一种绘制方法之一。

本文将对直角三角形法的相关知识进行详细解析。

什么是直角三角形法？在机械制图中，直角三角形法是一种绘制直线的方法。

所谓直角三角形法，就是利用直角三角形的性质，在平面上绘制出一条直线的方法。

直角三角形法的基本原理直角三角形法的基本原理是勾股定理，即直角三角形斜边的平方等于两条直角边的平方和。

在机械制图中，我们将一条已知直线和一个已知的与该直线垂直的直线相交，然后再根据勾股定理来确定需要绘制的直线的长度。

直角三角形法的具体步骤利用直角三角形法绘制一条直线的具体步骤如下：1.画出一条已知的直线和一个垂直于这条直线的线段（一般起点都是已知直线的端点），标出直角。

2.在这个直角三角形中，设直角边的长度为a，另一直角边的长度为b，斜边的长度为c。

3.根据勾股定理得到：c^2 = a^2 + b^2。

4.求出需要绘制的直线在这个直角三角形中对应的边的长度。

5.根据已知直线和垂直线段的位置，利用尺子在图纸上测量出需要绘制的直线的位置和长度。

直角三角形法的应用直角三角形法在机械制图中有着广泛的应用，比如绘制直线、绘制平行线、绘制角度等等。

在绘制机械零件的图纸时，它是非常常用的一种绘制方法。

注意事项在使用直角三角形法时，需要注意以下几点：1.按照要求绘制直角。

2.已知的直线和垂直线段必须准确无误地画在图纸上，否则会影响到绘制的直线的准确性。

3.在使用尺子测量需要绘制的直线的长度时，要确保尺子与图纸垂直，并且尺子上的刻度要准确无误。

直角三角形法是机械制图中非常常用的一种绘制方法。

在绘制机械零件的图纸时，掌握这种方法非常重要。

在使用直角三角形法绘制直线时，需要注意要按照要求绘制直角，并且已知的直线和垂直线段必须准确无误地画在图纸上，否则会影响到绘制的直线的准确性。

机械制图图纸的一般知识_第八讲、投影变换-工程第八讲投影变换1.知识要点（6）求一般位置直线的实长及其对投影面的夹角（7）求一般位置平面对投影面的夹角（8）求投影面垂直面的实形（9）综合举例2.教学设计求一般位置直线的实长及其对投影面的夹角有三种方法：直角三角形法、换面法、旋转法，我们只介绍前两种方法，而且把直角三角形法看成是换面法的特例；求一般位置平面的实形需要两次换面，我们分成两步讲解：求一般位置平面对投影面的夹角、求投影面垂直面的实形，。

3.课前准备准备教具和演示文稿。

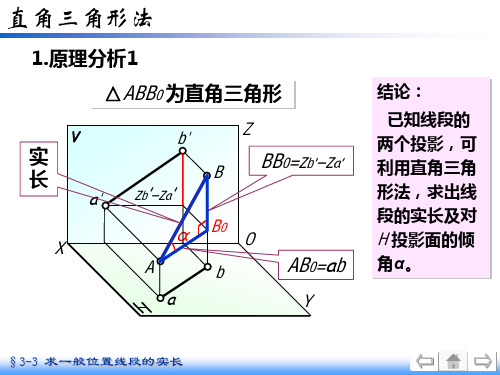
4.教学内容（1）求一般位置直线的实长及其对投影面的夹角1)直角三角形法直角三角形法的原理如图3-26所示，在直角三角形ABC中，AD=ab，BD=ΔZ（B和A点的Z坐标差），AB为空间直线AB的实长，∠BAD为直线AB和H面的夹角α，从投影图可知ab和B、A点的Z坐标差ΔZ，所以可画出直角ΔabE,使ΔabE≌ΔABD，则aE为空间直线AB的实长，∠baE为直线AB和H面的夹角α。

若求AB和V面的夹角β，可用a’b’和B、A点的Y坐标差ΔY为直角边作直角ΔabF，则∠Fa’b’为直线AB和V面的夹角β。

2)投影变换法一般位置直线可经过一次换面将其换成新投影面的平行线，在新投影面上的投影将反映空间直线对保留下来的旧投影面的夹角。

例如若要求空间直线对H面的夹角α和实长AB，可在由V、H面组成的投影体系中添加新投影面V1，使V1和H面垂直，和直线AB平行，则在由V1、H面组成的新投影体系中AB为正平线，且线段AB端点的Z坐标不变，所以可由原投影求出直线在V1面上的投影。

投影变换的原理如图3-27所示。

图3-26直角三角形法（制作动画）图3-27换面法的原理（1）（制作动画）若要求直线对V面的夹角β，可在由V、H面组成的投影体系中添加新投影面H1，使H1和V面垂直，和直线AB平行，则在由H1、V 面组成的新投影体系中AB为水平线，且线段AB端点的Y坐标不变，所以可由原投影求出直线在H1面上的投影。

试题1.直线AB与CD交叉，试求其公垂线的投影。

2.已知两直线投影如图所示，求其公垂线实长。

3.已知等腰直角三角形斜边BC，点A在V面上，且点A在BC的上方，完成三角形投影。

4.已知直角三角形ABC的一条直角边BC实长为40mm，且BC在直线DE上，试求ABC的投影。

5.已知等腰三角形ABC底边BC在BD上，补全三角形ABC的投影。

6. 已知菱形ABCD的正面投影a’b’c’d’以及水平投影ac，补全水平投影。

7. 已知正方形ABCD的一个顶点D在V面上，完成正方形ABCD的两面投影。

8.采用直角三角形法求直线AB对投影面的倾角α和β。

9.已知直线AB的实长为50mm，求a’b’。

10.已知直线AB对V面的倾角β=30°，求a’b’，并在AB上取点C，使AC=30mm。

答案1.直线AB与CD交叉，试求其公垂线的投影。

2.已知两直线投影如图所示，求其公垂线实长。

3.已知等腰直角三角形斜边BC，点A在V面上，且点A在BC的上方，完成三角形投影。

4.已知直角三角形ABC的一条直角边BC实长为40mm，且BC在直线DE上，试求ABC的投影。

5.已知等腰三角形ABC底边BC在BD上，补全三角形ABC的投影。

6. 已知菱形ABCD的正面投影a’b’c’d’以及水平投影ac，补全水平投影。

7. 已知正方形ABCD的一个顶点D在V面上，完成正方形ABCD的两面投影。

9.采用直角三角形法求直线AB对投影面的倾角α和β。

9.已知直线AB的实长为50mm，求a’b’。

10.已知直线AB对V面的倾角β=30°，求a’b’，并在AB上取点C，使AC=30mm。

试题1.直线AB与CD交叉，试求其公垂线的投影。

2.已知两直线投影如图所示，求其公垂线实长。

3.已知等腰直角三角形斜边BC，点A在V面上，且点A在BC的上方，完成三角形投影。

4.已知直角三角形ABC的一条直角边BC实长为40mm，且BC在直线DE上，试求ABC的投影。

5.已知等腰三角形ABC底边BC在BD上，补全三角形ABC的投影。

6. 已知菱形ABCD的正面投影a’b’c’d’以及水平投影ac，补全水平投影。

7. 已知正方形ABCD的一个顶点D在V面上，完成正方形ABCD的两面投影。

8.采用直角三角形法求直线AB对投影面的倾角α和β。

9.已知直线AB的实长为50mm，求a’b’。

10.已知直线AB对V面的倾角β=30°，求a’b’，并在AB上取点C，使AC=30mm。

答案1.直线AB与CD交叉，试求其公垂线的投影。

2.已知两直线投影如图所示，求其公垂线实长。

3.已知等腰直角三角形斜边BC，点A在V面上，且点A在BC的上方，完成三角形投影。

4.已知直角三角形ABC的一条直角边BC实长为40mm，且BC在直线DE上，试求ABC的投影。

5.已知等腰三角形ABC底边BC在BD上，补全三角形ABC的投影。

6. 已知菱形ABCD的正面投影a’b’c’d’以及水平投影ac，补全水平投影。

7. 已知正方形ABCD的一个顶点D在V面上，完成正方形ABCD的两面投影。

9.采用直角三角形法求直线AB对投影面的倾角α和β。

9.已知直线AB的实长为50mm，求a’b’。

10.已知直线AB对V面的倾角β=30°，求a’b’，并在AB上取点C，使AC=30mm。