最短航线和两点间距离

最短航线问题是一个在地理学和交通规划中常见的问题，它涉及到确定两点之间最短的飞行或旅行路线。

这个问题通常需要考虑地球的形状、障碍物（如山脉、海洋等）、天气条件等多种因素。

下面是一个最短航线问题的例子：
1. 假设我们要从点A（经度10°W，纬度20°N）飞往点B （经度60°E，纬度50°S）。

请计算最短的航线距离。

2. 考虑地球的球面性质，以及地球上两点之间的最短距离是通过大圆弧来衡量的，即两点之间的最短距离是沿着地球表面的大圆线段来计算的。

3. 考虑到地球的经纬度坐标，我们可以使用经纬度的差值来计算两点之间的距离。

具体来说，我们可以使用以下公式来计算两点之间的距离：
Distance = R × arccos(sin(lat1) × sin(lat2) + cos(lat1) × cos(lat2) × cos(lon2 - lon1))
其中，R是地球的半径（大约为6371公里），lat1和lon1是起点A的纬度和经度，lat2和lon2是终点B的纬度和经度。

根据上述公式，我们可以计算出点A和点B之间的最短航线距离。

航线最低间隔的安全要求介绍在民航领域，航线最低间隔是指两架飞机之间可以保持的最小水平和垂直距离。

由于飞机在飞行时可能出现不同的情况，包括天气、机械故障等，因此航线最低间隔是确保飞机在飞行过程中安全的重要因素之一。

国际标准国际民航组织（ICAO）是制定航线最低间隔标准的国际组织之一。

目前，ICAO 规定的最低间隔标准为：在水平方向上，当两架飞机的速度相同时，最小间隔为5海里；在垂直方向上，最小间隔为1000英尺。

此外，ICAO还规定了一些特殊情况下的最低间隔标准。

例如，在飞机起飞和降落过程中，最小间隔将会更短。

美国标准美国联邦航空管理局（FAA）是负责制定航线最低间隔标准的机构。

FAA所制定的标准与ICAO保持一致，即最小间隔为5海里和1000英尺。

除此之外，FAA还制定了一些特殊情况下的最低间隔标准。

例如，在飞机起飞和降落过程中，最小间隔将会更短。

实际应用航线最低间隔的应用是非常广泛的。

在飞机执行起飞和降落任务时，航线最低间隔可以确保飞机安全地并进离机场。

在飞机巡航的过程中，航线最低间隔可以确保飞机不会相互干扰，保持安全距离。

此外，航线最低间隔还可以对飞行员的驾驶技能进行测试和评估。

在飞机进行着陆时，飞行员需要确保飞机安全地降落在跑道上，而航线最低间隔可以让他们更好地掌握飞机的高度和速度。

结论航线最低间隔是一项重要的安全要求，能够为飞机的飞行提供有力的保障。

国际上已有统一的标准，各国民航机构都会按照这些标准来执行。

在实际应用时，航线最低间隔可以确保飞机的安全，同时也能对飞行员的技能进行测试和评估，为整个民航行业的安全发展提供了保障。

利用经纬网定“最短航线”★★★★○○○1.最短航线的概念地球上两点间最短航线为球面最短距离，即经过两点的大圆劣弧长度。

(注：所谓大圆指过地心的平面与球面的交线)①同一经度上的两点，其最短距离的劣弧线就在经线上(如图中AB)。

②同一纬线上的两点，其最短距离的劣弧线向较高纬度凸(如图中同一条纬线上MK之间的最短航线是MPK而不是MQK)。

③由于晨昏线本身就是一个大圆，故处在晨昏线上的两点最短航线就是两点之间的最短晨昏线(即最短劣弧线)。

2.最短航线的判断方法球面最短距离是一段弧，该弧线的确定可依据下面两个步骤进行。

(1)确定“大圆”：“大圆”即球面两点所在的过球心的平面与球面的交线。

①在地球上，三种情况下“大圆”是确定的。

如下图所示。

②非赤道的纬线上两点，所在“大圆”具有以下特征：a.北半球——大圆向北极方向倾斜；b.南半球——大圆向南极方向倾斜。

(2)确定“劣弧”：大圆上两点间的最短距离具体应该是哪一段弧线，则由“劣弧”来决定，所谓“劣弧”，即两点间的弧度小于180°。

如图6中的两段劣弧。

如果记忆不牢固的话，可通过下图进行推导。

如图A、B为位于北半球的两点且不在常见的大圆上，则其最短航线为一个向北弯曲的弧线，C、D为位于南半球的两点且不在常见的大圆上，则其最短航线为一个向南弯曲的弧线。

具体是：同北偏北，同南偏南，同一条经线圈上走极点。

寻“最短航线”的技巧(1)若两地经度差等于180°，过这两点的大圆便是经线圈。

最短航线经过两极点，具体分三种情况：①同在北半球，先向北，过极点后再向南，如A到E。

②同在南半球，先向南，过极点后再向北，如B到D。

③两地位于不同半球，则看劣弧过哪个极点再做讨论，如A至C。

(2)同一纬线上但不在同一经线圈上①同在北纬，从A到B的最短距离；先向东北，再向东南方向。

②同在南纬，从A到B的最短距离：先向东南，再向东北方向。

读下图，从E点到F点的最短航线是( )A．先西北后西南 B．先东南后东北C．先西南后西北 D．先东北后东南【答案】A某飞行员驾机从A机场(30°N,120°E)起飞，为了经济省时，飞机必须沿最短航线飞往B机场(35°S,60°W)执行任务。

怎么用经纬度计算两地之间的距离经纬度是地球上一点的坐标表示方法，可以用来计算两个点之间的距离。

计算两地之间的距离可以使用多种方法，包括球面距离公式、大圆航线距离和Vincenty算法等。

下面将详细介绍这些方法。

1.球面距离公式球面距离公式是最简单且最常用的计算两点之间距离的方法。

它基于球面三角形的边长计算两点之间的距离，如下所示：d = R * arccos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1))其中，d是两点之间的球面距离，R是地球的平均半径，lat1和lat2是两点的纬度，lon1和lon2是两点的经度。

2.大圆航线距离大圆航线距离是计算两点之间最短距离的方法，它基于地球表面上连接两点的最短弧线，如下所示：d = R * arccos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1))其中，d是两点之间的大圆航线距离，R是地球的半径，lat1和lat2是两点的纬度，lon1和lon2是两点的经度。

3. Vincenty算法Vincenty算法是一种更精确的计算两点之间距离的方法，它基于椭球体模型而不是简单地球模型。

该算法能够考虑地球形状的扁平化，并且适用于短距离和长距离的计算。

具体实现需要迭代计算，公式略显繁琐，如下所示：a=R1,b=R2,f=(a-b)/aL = L2 - L1, U1 = atan((1 - f) * tan(lat1)), U2 = atan((1 - f) * tan(lat2))sinU1 = sin(U1), cosU1 = cos(U1), sinU2 = sin(U2), cosU2 = cos(U2)λ=L,λʹ=2πwhile (，λ - λʹ， > 10e-12):sinλ = sin(λ), cosλ = cos(λ), sinσ = sqrt((cosU2 *sinλ) * (cosU2 * sinλ) + (cosU1 * sinU2 - sinU1 * cosU2 *cosλ) * (cosU1 * sinU2 - sinU1 * cosU2 * cosλ))cosσ = sinU1 * sinU2 + cosU1 * cosU2 * cosλσ = atan2(sinσ, cosσ)sinα = cosU1 * cosU2 * sinλ / sinσcos²α = 1 - sinα * sinαcos2σm = cosσ - 2 * sinU1 * sinU2 / cos²αC = f / 16 * cos²α * (4 + f * (4 - 3 * cos²α))λʹ=λλ = L + (1 - C) * f * sinα * (σ + C * sinσ * (cos2σm + C * cosσ * (-1 + 2 * cos2σm * cos2σm)))u² = cos²α * (a*a - b*b) / (b*b)B=u²/1024*(256+u²*(-128+u²*(74-47*u²)))Δσ = B / 6 * (cosσ * (-1 + 2 * cos2σm * cos2σm) - B / 4 * (cos2σm * (-3 + 4 * sinσ * sinσ) - B / 6 * cosσ * (-3 + 4 * cos2σm * cos2σm) * (-3 + 4 * sinσ * sinσ)))s=b*A*(σ-Δσ)其中，a和b是地球的长半轴和短半轴，f是扁平度参数，R1和R2是两点的曲率半径，L1和L2是两点的经度差，lat1和lat2是两点的纬度。

多个地点间的距离计算公式在现代社会，人们经常需要计算不同地点之间的距离，比如出行规划、物流配送等。

而地点之间的距离计算公式就成为了一个重要的工具。

本文将介绍一些常用的地点间距离计算公式，并对它们进行简要的分析和比较。

1. 直线距离计算公式。

直线距离是最简单的距离计算方式，它是通过两个地点的经纬度坐标来计算的。

假设地点A的经纬度坐标为（A1, A2），地点B的经纬度坐标为（B1, B2），则地点A和地点B之间的直线距离可以通过以下公式计算：d = R arccos(sin(A1)sin(B1) + cos(A1)cos(B1)cos(A2-B2))。

其中，R为地球半径，一般取平均值6371km。

这个公式的优点是简单易用，缺点是没有考虑地球表面的曲率和地形的影响，只适用于较短距离的计算。

2. 大圆航线距离计算公式。

大圆航线距离是指两地之间在地球表面上的最短距离，也是飞行航线的最佳路径。

它的计算公式如下：d = R arccos(sin(A1)sin(B1) + cos(A1)cos(B1)cos(A2-B2))。

这个公式与直线距离的公式是相同的，但它更适用于长距离的计算，因为它考虑了地球表面的曲率。

在航空航线规划和航海导航中广泛使用。

3. 曼哈顿距离计算公式。

曼哈顿距离是指两点在标准坐标系上的距离，即沿着坐标轴的距离之和。

对于二维坐标系来说，两点（x1, y1）和（x2, y2）之间的曼哈顿距离可以通过以下公式计算：d = |x1 x2| + |y1 y2|。

这个公式的优点是简单直观，适用于城市道路网格等直线交错的环境，缺点是没有考虑地球曲面的影响。

4. Haversine距离计算公式。

Haversine距离是一种用于计算两点间球面距离的方法，它考虑了地球的曲率和地球半径的变化。

对于地球上两点之间的距离，Haversine距离的计算公式如下：a = sin²((Δφ)/2) + cos(φ1) cos(φ2) sin²((Δλ)/2)。

最短航线的三种判定方法以最短航线的三种判定方法为标题，写一篇文章一、最短航线的定义与重要性最短航线是指在给定的起点和终点之间选择的距离最短的航行路径。

在航空、航运和航天领域，寻找最短航线对于节省时间、燃料和资源具有重要意义。

为了确定最短航线，有三种常用的判定方法：直线距离法、曲线距离法和大圆航线法。

二、直线距离法直线距离法是最简单的判定方法，它基于两点间的直线距离。

这种方法忽略了地球的曲率和地球表面的不规则性，只考虑了两点之间的直线距离。

在实际应用中，直线距离法常用于短距离航线的计算，例如城市之间的航线。

然而，当航线跨越较大的距离时，直线距离法会引入较大的误差，因为地球的曲率不能被忽略。

三、曲线距离法曲线距离法是一种考虑地球表面曲率的判定方法。

它通过在地球表面上选择一条曲线路径来计算航线距离。

常用的曲线路径包括大圆弧和小圆弧。

大圆弧是连接两个点的最短路径，它是地球表面上的一段大圆。

小圆弧是连接两个点的路径，它不一定是最短路径，但比直线距离更接近最短航线。

曲线距离法考虑了地球的曲率，因此可以在计算较长航线时提供更准确的结果。

四、大圆航线法大圆航线法是寻找最短航线的一种常用方法，它基于大圆弧路径。

大圆弧是连接两个点的最短路径，它是地球表面上的一段大圆。

在计算大圆航线时，需要使用球面三角学公式，如球面余弦定理和球面正弦定理。

这些公式可以根据给定的起点和终点的经纬度来计算大圆航线的距离和方向。

大圆航线法是最精确的判定方法之一，广泛应用于航空和航运领域。

五、总结最短航线的判定方法有直线距离法、曲线距离法和大圆航线法。

直线距离法简单易用，适用于短距离航线的计算。

曲线距离法考虑了地球的曲率，提供了更准确的结果。

大圆航线法是最精确的判定方法之一，广泛应用于航空和航运领域。

在实际应用中，选择适当的判定方法可以帮助我们找到最短航线，节省时间和资源。

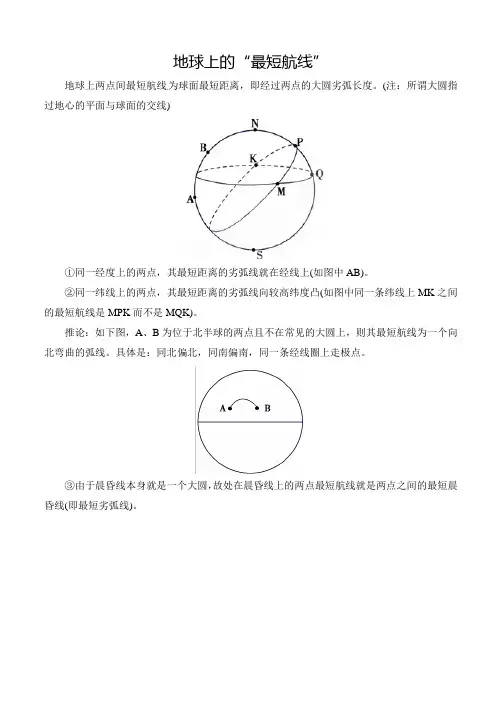
地球上的“最短航线”
地球上两点间最短航线为球面最短距离，即经过两点的大圆劣弧长度。

(注：所谓大圆指过地心的平面与球面的交线)
①同一经度上的两点，其最短距离的劣弧线就在经线上(如图中AB)。

②同一纬线上的两点，其最短距离的劣弧线向较高纬度凸(如图中同一条纬线上MK之间的最短航线是MPK而不是MQK)。

推论：如下图，A、B为位于北半球的两点且不在常见的大圆上，则其最短航线为一个向北弯曲的弧线。

具体是：同北偏北，同南偏南，同一条经线圈上走极点。

③由于晨昏线本身就是一个大圆，故处在晨昏线上的两点最短航线就是两点之间的最短晨昏线(即最短劣弧线)。

2020届高三地理复习讲解：如何合理选择“最短航线”一、知识讲解地球上两点间最短航线为球面最短距离，即经过两点的大圆劣弧长度。

(注：所谓大圆指过地心的平面与球面的交线)1．同一经线上的两点，其最短距离的劣弧线就在其经线上(如图中)。

经度相对的两点，其最短距离的劣弧线是经线圈的一段，最短距离过极点(如图中)。

2．同一纬线上的两点(赤道除外)，其最短距离的劣弧线向较高纬度凸(如图中同一条纬线上MK之间的最短航线是，而不是)。

[特别提醒]地球上有三种大圆是确定的，如下图所示：3．航向的判读(以图中从M点到K点最短航线为例)：(1)首先判读两点的东西相对位置。

K点(目的地)在M点东侧，若想到达K点必须向东航行。

(2)航行过程需要经过较高纬的P点，故需要先向较高纬(向北)航行，后向较低纬(向南)航行。

(3)结合上面两点分析，其航行方向为东北(—正东)—东南。

二、典题示例(2019·宁波一模)一架速度为800 km/h的飞机从我国海口市(20°N,110°E)直飞M地(20°S,70°W)，行程约需()A．20 h B．25 hC．45 h D．15 h[解题步骤]第一步：根据题干材料关键信息“直飞”的要求，飞机要按照“最短航线”飞行。

第二步：寻找最短航线：结合两地经纬度可知，两地关于地心对称，则其飞行最短航线是经过两地的任意大圆。

第三步：两地最短距离应为2万km，速度为800 km/h，可计算飞机需要飞行约25 h 到达M地。

[答案] B三、跟踪训练1．新加坡(采用的是东八区的计时方法)是亚洲与大洋洲的航空枢纽，也是伦敦到悉尼的重要航空中转站。

由新加坡沿最短线路飞往伦敦的航班()A．航程小于10 000 km B．航程大于15 000 kmC．航向一直朝西北D．航向先向西北再向西南解析：选D最短航线所跨的经度小于180°，故整体向西飞，但在同一半球中跨经度大于90°，则有方向上的拐点，故航向先向西北再向西南。

地球表面上两点间最短距离（航线）方向的确定作者：***来源：《中学政史地·高中文综》2016年第03期在复习经纬网的内容时，地球表面上两点间最短航线方向的确定，是我们的拦路虎。

由于有的同学对这类问题缺乏足够的空间想象能力，只是机械地背一些结论，造成在解这类试题时经常出错。

针对有些同学空间想象能力和数学水平不太高等情况，本文旨在帮助他们全面正确认识地球表面上两点间最短航线方向的确定问题。

地球表面上两点之间的最短航线，指的是两点所在大圆的劣弧。

一、认识大圆过球面上两点的大圆就是经过这两点以地心为圆心的圆。

在地球上有三种情况大圆是确定的，如图1中的赤道、经线圈、晨昏圈。

在图2中，很显然，甲、乙、丙所在圆的圆心是地心，其所在的圆就是大圆，其他的圆都不是大圆。

二、确定劣弧大圆上两点间的最短航线或距离就是两点所在大圆的劣弧。

所谓劣弧，即两点间的弧度小于180°。

如图3中的⌒AB和⌒CD都是过大圆的劣弧，而⌒EF虽然是劣弧，但不是大圆上的劣弧。

图4中甲和乙之间的弧线，只有最上面的弧是过大圆的劣弧。

三、确定地球上两点间最短航线的方向沿着劣弧的行进方向就是最短航线的方向。

1.两点在同一经线圈上或者在赤道上（1）两点在同一经线上，向正北或向正南走，不转向。

如图5， A到B是向正北走；反之，B到A是向正南走。

（2）两点在两条经线上（经度相对，两点的经度差等于180°），过极点要转向。

如在通过北极点之前，先向正北走，过北极点后转向正南；反之，在通过南极点之前，先向正南走，过南极点后转向正北。

如图6，从A到B先向正北走，过北极点后向正南走；从B 到A是先向正北走，过北极点后向正南走。

（3）两点在赤道上，向正东走或向正西走，不转向。

如图7， A到B是向正东走；反之，B到A是向正西走。

2.两点既不在同一经线上，也不在赤道上地球上任意两点和地心必然确定一个大圆，一定存在一个纬线圈和这个大圆相切，切点即为这个大圆的纬度最高点，若大圆劣弧航线经过切点，则发生转向，转向点为切点；若大圆劣弧航线不经过切点，则不发生转向。

国内航线距离清单一、北京飞往上海北京和上海之间的航线是国内最繁忙的航线之一。

这两个城市分别是中国的首都和经济中心，每天都有大量的人员往返于两地。

北京到上海的直线距离约为1062公里，飞行时间大约为2小时。

二、广州飞往深圳广州和深圳是中国南方地区两个重要的经济中心。

两地之间的航线非常短，直线距离仅为136公里，飞行时间约为30分钟。

由于两地之间的交通便利，很多商务人士和旅客选择坐飞机往返。

三、成都飞往重庆成都和重庆是中国西南地区的两个重要城市。

两地之间的航线非常短，直线距离约为312公里，飞行时间约为1小时。

成都和重庆之间的航班频繁，为西南地区的旅客提供了便捷的交通方式。

四、哈尔滨飞往长春哈尔滨和长春是中国东北地区的两个重要城市。

两地之间的航线相对较短，直线距离约为304公里，飞行时间约为1小时。

这条航线不仅连接了两个城市，也方便了周边地区的人员往来。

五、西安飞往兰州西安和兰州是中国西北地区的两个重要城市。

两地之间的航线较长，直线距离约为615公里，飞行时间约为1小时30分钟。

这条航线连接了陕西和甘肃两个省份，为两地的经济交流和人员往来提供了便利。

六、南京飞往杭州南京和杭州是中国东南地区的两个重要城市。

两地之间的航线相对较短，直线距离约为236公里，飞行时间约为50分钟。

这条航线不仅连接了两个城市，也方便了周边地区的人员往来。

七、武汉飞往长沙武汉和长沙是中国中部地区的两个重要城市。

两地之间的航线较短，直线距离约为345公里，飞行时间约为1小时。

这条航线不仅连接了两个城市，也方便了周边地区的人员往来。

八、青岛飞往大连青岛和大连是中国东北地区的两个重要港口城市。

两地之间的航线相对较短，直线距离约为463公里，飞行时间约为1小时20分钟。

这条航线为两地的经济交流和人员往来提供了便利。

以上是国内一些常见航线的距离清单，这些航线连接了中国各地的重要城市，为人们的出行和经济交流提供了便利。

无论是商务出差还是旅游观光，航线的短距离和快速飞行时间都为人们提供了更加便捷的选择。

例谈地球表面两点之间的最短航线问题地球是一个两极部位略扁的不规则球体，但在讨论两点之间的最短航线时，一般近似地认为地球是一个正球体，即在地球表面上两地之间的最短距离（或航线）应指的是经过这两点的球大圆在这两点间的一段劣弧长度，这个圆的圆心必须经过球心(即地心)。

在中学地理应试中主要有以下几种情况。

1.晨昏线上两点之间的最短距离是该晨昏线上两点之间的劣弧部分。

如图1右图中的的阴影部分为黑夜,GH之间的最短航线是沿着晨昏线的劣弧走：先东南，再向正东，后东北，即经过GMH，而不是GYH。

2.赤道上两点之间的最短距离是赤道上两点之间的劣弧部分。

如图1左图中的AB之间的最短航线：A到B走为正东或B到A走为正西。

3.经线上两点之间的最短距离是该经线上两点之间劣弧部分。

如图1左图中的CD之间的最短航线：C到D为正北或D到A为正南。

4.若两地间的经度差等于180°，则经过两点的大圆一定是经线圈。

这两点间的最短航程须经过极点，其结果只能是先正北后正南或先正南后正北。

⑴同位于北半球的两点，最短航线必须经过北极点，其航行方向一定是先向正北，过北极点后再向正南。

如图1左图中的EF之间的最短航线为先正北后正南，即经过ENF三个点的经线圈的劣弧线,而不是沿EF的纬线走。

⑵同位于南半球的两点，最短航线必须经过南极点，其航行方向一定是先向正南，过北极点后再向正北。

⑶两地位于不同半球时，这时需要考虑是经过北极点为劣弧，还是经过南极点为劣弧，然后再确定最短航程的走向。

如图1左图中的E点到X点的最短航线为先正北后正南，即经过经线圈的ENFX 四个点的劣弧线；而不是先正南后正北，即不是经过经线圈的ESX三个点弧线。

注意：上述四种情况中赤道、经线、经线圈、晨昏线都是大圆或大圆的一部分，故直接可截取球面距离。

5.若两地经度差不等于180°，则过两地的大圆不是经线圈，而是与经线圈斜交，其最短航线不经过极点，具体分两种情况。