两点间最短航线

大圆劣弧的最短航线原则
大圆弧的最短航线原则是指在球面上，两点之间的最短距离是大圆弧上的航线。

地球是一个近似于球体的天体，所以当飞机或船只在地球表面上从一个点飞往另一个点时，航线通常是沿着地球表面上的大圆弧进行。

大圆弧是将球体分成两个相等的半球的圆弧。

它是球面上两点之间距离最短的路径，贯穿了球体的中心。

使用大圆弧航线可以节省时间和燃料，因为它是最短的路径。

另外，使用大圆弧航线可以更好地适应地球的曲率，从而减少路径上的平均速度变化。

因此，在航空和航海导航中，大圆弧航线被广泛使用，以提高效率和准确性。

知识点最短航线地球表面，任意两点A、B间的最短航线，是过这两点的大圆（以地心为圆心，过A、B两点的圆）的劣弧。

最短距离的规律如下：①两点位于同一条经线：沿着该条经线，两点间的劣弧（距离较短的弧），即为最短距离；②两点经度和为180°：两条经线恰好组成一个“大圆”。

过南极点（或北极点）的两点间的劣弧，即为最短距离；③两点位于同一条纬线：北半球航线偏北，南半球航线偏南（凸向高纬）；④两点位于赤道上：沿着赤道，两点间的劣弧（距离较短的弧），即为最短距离；⑤其他情况：北半球航线偏北，南半球航线偏南（凸向高纬）。

如下图所示，A、B两点位于北半球的同一条纬线，则由A点到B点的最短航线，凸向北极点，即从A点先向东北、再向东南。

图1 两点间的最短距离（北半球）晨昏线地球上白天与黑夜的分界线，叫做“晨昏线”。

地球的自转方向为自西向东，顺着自转的方向，由黑夜进入白天的分界线，叫做晨线；由白天进入黑夜的分界线，叫做昏线。

根据晨昏线，可以判断时间、季节、太阳直射点的经纬度和日出时间：①判断时间。

晨线与赤道的交点为早上6:00，昏线与赤道的交点为晚上18:00；夜半球的中央经线为0:00，昼半球的中央经线为正午12:00；②判断季节。

a）晨昏线与北极圈相交，且北极圈以北一直处于白天，则为夏至；若北极圈以北一直处于黑夜，则为冬至；b）晨昏线与北极点相交，则为春分或者秋分；③判断太阳直射点的经纬度。

a）昼半球的中央经线，即为太阳直射点的经度；b）太阳直射点的纬度=90°-晨昏圈最北端的纬度，例如晨昏圈最北端为66°34′N（北极圈），则此时太阳直射点的纬度为23°26′N或23°26′S，然后根据北极点的极昼极夜情况，进一步确定太阳直射点的位置。

④日出时间。

晨线上的地点，同时日出。

在夏季，北半球晨昏线向西倾斜，晨昏线上同时日出，因此同一经线上，纬度越高，日出越早；在冬季，北半球晨昏线向东倾斜，因此同一条经线上，纬度越高，日出越晚。

最短航线的三种判定方法以最短航线的三种判定方法为标题，写一篇文章一、最短航线的定义与重要性最短航线是指在给定的起点和终点之间选择的距离最短的航行路径。

在航空、航运和航天领域，寻找最短航线对于节省时间、燃料和资源具有重要意义。

为了确定最短航线，有三种常用的判定方法：直线距离法、曲线距离法和大圆航线法。

二、直线距离法直线距离法是最简单的判定方法，它基于两点间的直线距离。

这种方法忽略了地球的曲率和地球表面的不规则性，只考虑了两点之间的直线距离。

在实际应用中，直线距离法常用于短距离航线的计算，例如城市之间的航线。

然而，当航线跨越较大的距离时，直线距离法会引入较大的误差，因为地球的曲率不能被忽略。

三、曲线距离法曲线距离法是一种考虑地球表面曲率的判定方法。

它通过在地球表面上选择一条曲线路径来计算航线距离。

常用的曲线路径包括大圆弧和小圆弧。

大圆弧是连接两个点的最短路径，它是地球表面上的一段大圆。

小圆弧是连接两个点的路径，它不一定是最短路径，但比直线距离更接近最短航线。

曲线距离法考虑了地球的曲率，因此可以在计算较长航线时提供更准确的结果。

四、大圆航线法大圆航线法是寻找最短航线的一种常用方法，它基于大圆弧路径。

大圆弧是连接两个点的最短路径，它是地球表面上的一段大圆。

在计算大圆航线时，需要使用球面三角学公式，如球面余弦定理和球面正弦定理。

这些公式可以根据给定的起点和终点的经纬度来计算大圆航线的距离和方向。

大圆航线法是最精确的判定方法之一，广泛应用于航空和航运领域。

五、总结最短航线的判定方法有直线距离法、曲线距离法和大圆航线法。

直线距离法简单易用，适用于短距离航线的计算。

曲线距离法考虑了地球的曲率，提供了更准确的结果。

大圆航线法是最精确的判定方法之一，广泛应用于航空和航运领域。

在实际应用中，选择适当的判定方法可以帮助我们找到最短航线，节省时间和资源。

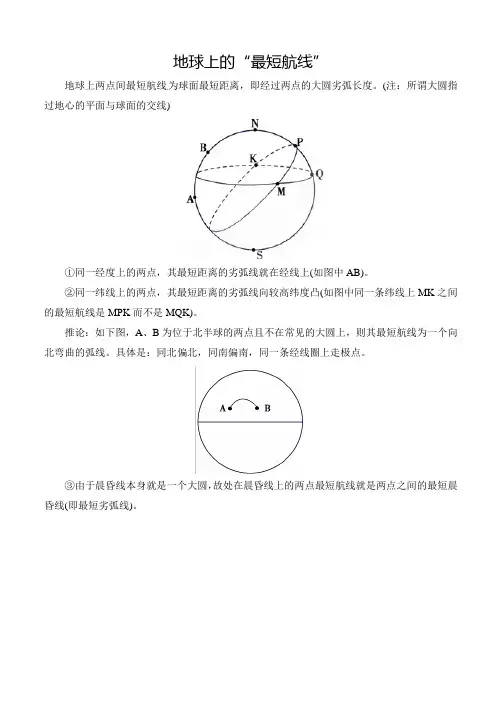
地球上的“最短航线”
地球上两点间最短航线为球面最短距离，即经过两点的大圆劣弧长度。

(注：所谓大圆指过地心的平面与球面的交线)
①同一经度上的两点，其最短距离的劣弧线就在经线上(如图中AB)。

②同一纬线上的两点，其最短距离的劣弧线向较高纬度凸(如图中同一条纬线上MK之间的最短航线是MPK而不是MQK)。

推论：如下图，A、B为位于北半球的两点且不在常见的大圆上，则其最短航线为一个向北弯曲的弧线。

具体是：同北偏北，同南偏南，同一条经线圈上走极点。

③由于晨昏线本身就是一个大圆，故处在晨昏线上的两点最短航线就是两点之间的最短晨昏线(即最短劣弧线)。

利用经纬网定“最短航线”★★★★○○○1.最短航线的概念地球上两点间最短航线为球面最短距离，即经过两点的大圆劣弧长度。

(注：所谓大圆指过地心的平面与球面的交线)①同一经度上的两点，其最短距离的劣弧线就在经线上(如图中AB)。

②同一纬线上的两点，其最短距离的劣弧线向较高纬度凸(如图中同一条纬线上MK之间的最短航线是MPK而不是MQK)。

③由于晨昏线本身就是一个大圆，故处在晨昏线上的两点最短航线就是两点之间的最短晨昏线(即最短劣弧线)。

2.最短航线的推断方法球面最短距离是一段弧，该弧线的确定可依据下面两个步骤进行。

(1)确定“大圆”：“大圆”即球面两点所在的过球心的平面与球面的交线。

①在地球上，三种状况下“大圆”是确定的。

如下图所示。

②非赤道的纬线上两点，所在“大圆”具有以下特征：a.北半球——大圆向北极方向倾斜；b.南半球——大圆向南极方向倾斜。

(2)确定“劣弧”：大圆上两点间的最短距离详细应当是哪一段弧线，则由“劣弧”来确定，所谓“劣弧”，即两点间的弧度小于180°。

如图6中的两段劣弧。

假如记忆不坚固的话，可通过下图进行推导。

如图A、B为位于北半球的两点且不在常见的大圆上，则其最短航线为一个向北弯曲的弧线，C、D为位于南半球的两点且不在常见的大圆上，则其最短航线为一个向南弯曲的弧线。

详细是：同北偏北，同南偏南，同一条经线圈上走极点。

寻“最短航线”的技巧(1)若两地经度差等于180°，过这两点的大圆便是经线圈。

最短航线经过两极点，详细分三种状况：①同在北半球，先向北，过极点后再向南，如A到E。

②同在南半球，先向南，过极点后再向北，如B到D。

③两地位于不同半球，则看劣弧过哪个极点再做探讨，如A至C。

(2)同一纬线上但不在同一经线圈上①同在北纬，从A到B的最短距离；先向东北，再向东南方向。

②同在南纬，从A到B的最短距离：先向东南，再向东北方向。

读下图，从E点到F点的最短航线是()A．先西北后西南 B．先东南后东北C．先西南后西北 D．先东北后东南【答案】A某飞行员驾机从A机场(30°N,120°E)起飞，为了经济省时，飞机必需沿最短航线飞往B机场(35°S,60°W)执行任务。

最短航线公式
嘿，朋友们！今天咱来聊聊最短航线公式。

你知道吗，这就像是在大海中寻找最快捷的路径一样神奇！
比如说球面上两点间的最短航线公式，那就是沿着大圆劣弧走就对啦！就好比你要从北京去纽约，直接沿着那个大圆弧飞过去，可别乱跑呀！这多简单易懂呀！
还有计算同纬度两点间最短航线呢，不就是先向高纬凸出，再沿大圆劣弧飞嘛！哎呀呀，就像你要从上海到悉尼，先朝着高纬方向飞一段，再沿着合适的弧飞过去，这样不就最快啦！
再比如不同半球两点间的最短航线，先确定大圆，再找劣弧呀！就如同你要从南非去阿根廷，得找好那个最佳路线呀！
所以说呀，这些最短航线公式真的超级有用，能让我们在飞行或者航海中少走好多冤枉路呢！大家一定要记住哦！。

最短航线的三种概况航线是指飞机、船舶等交通工具在空中、水上或陆地上设定的飞行或航行路线。

在航空和航海领域中，寻找最短航线是一项重要的任务，因为最短航线可以减少时间、节省燃料和提高运输效率。

本文将介绍三种寻找最短航线的方法。

第一种方法是利用大圆航线。

大圆航线是连接地球上两点的最短弧线，它是球面上的一个圆周。

在地球上，经线和纬线形成了一个网格系统。

如果我们直接连接两个点，会发现它们之间的航线并不一定是直线，而是一个曲线。

为了找到最短航线，可以利用大圆航线的概念。

大圆航线是连接两点的最短路径，它是球面上的一条弧线。

通过计算两点之间的经纬度，再利用球面三角学的原理，可以确定大圆航线的路径。

第二种方法是利用航空公司的航线规划系统。

航空公司通常拥有自己的航线规划系统，这些系统可以帮助航空公司确定最短航线。

这些系统考虑了飞行距离、空域限制、气象条件等因素，并利用数学模型和算法来计算最优航线。

航空公司可以根据不同的需求和限制，调整航线规划系统的参数，以求得最短航线。

第三种方法是利用航行规划软件。

航行规划软件是专门为船舶设计的软件，它可以帮助船舶确定最短航线。

航行规划软件考虑了许多因素，如航行速度、潮汐、水深、海流、风向等，通过计算这些因素的影响，确定最短航线。

航行规划软件通常使用电子海图和船舶相关的数据，可以根据不同的船舶类型和特点，为船舶提供最佳的航线。

寻找最短航线是一项复杂的任务，需要考虑许多因素。

大圆航线、航空公司的航线规划系统和航行规划软件是三种常用的方法。

通过这些方法，航空公司和船舶可以找到最短航线，提高运输效率，节省时间和资源。

随着技术的不断发展，寻找最短航线的方法也会不断改进和完善，为航空和航海领域的发展做出更大的贡献。

例谈地球表面两点之间的最短航线问题地球是一个两极部位略扁的不规则球体，但在讨论两点之间的最短航线时，一般近似地认为地球是一个正球体，即在地球表面上两地之间的最短距离（或航线）应指的是经过这两点的球大圆在这两点间的一段劣弧长度，这个圆的圆心必须经过球心(即地心)。

在中学地理应试中主要有以下几种情况。

1.晨昏线上两点之间的最短距离是该晨昏线上两点之间的劣弧部分。

如图1右图中的的阴影部分为黑夜,GH之间的最短航线是沿着晨昏线的劣弧走：先东南，再向正东，后东北，即经过GMH，而不是GYH。

2.赤道上两点之间的最短距离是赤道上两点之间的劣弧部分。

如图1左图中的AB之间的最短航线：A到B走为正东或B到A走为正西。

3.经线上两点之间的最短距离是该经线上两点之间劣弧部分。

如图1左图中的CD之间的最短航线：C到D为正北或D到A为正南。

4.若两地间的经度差等于180°，则经过两点的大圆一定是经线圈。

这两点间的最短航程须经过极点，其结果只能是先正北后正南或先正南后正北。

⑴同位于北半球的两点，最短航线必须经过北极点，其航行方向一定是先向正北，过北极点后再向正南。

如图1左图中的EF之间的最短航线为先正北后正南，即经过ENF三个点的经线圈的劣弧线,而不是沿EF的纬线走。

⑵同位于南半球的两点，最短航线必须经过南极点，其航行方向一定是先向正南，过北极点后再向正北。

⑶两地位于不同半球时，这时需要考虑是经过北极点为劣弧，还是经过南极点为劣弧，然后再确定最短航程的走向。

如图1左图中的E点到X点的最短航线为先正北后正南，即经过经线圈的ENFX 四个点的劣弧线；而不是先正南后正北，即不是经过经线圈的ESX三个点弧线。

注意：上述四种情况中赤道、经线、经线圈、晨昏线都是大圆或大圆的一部分，故直接可截取球面距离。

5.若两地经度差不等于180°，则过两地的大圆不是经线圈，而是与经线圈斜交，其最短航线不经过极点，具体分两种情况。

如何确定地球表面两点间最短航线的方向在近年的地理试题中，考查地球上两点间最短航线的方向问题经常出现，由于很多学生对这类问题没有从本质上搞清楚，又缺乏空间想象能力，只是机械地背一些结论，造成解这类题目时经常出错。

本文对此问题简单归纳如下。

判读依据：数学知识：球面上两点间的最短距离为两点所在大圆的劣弧。

地理知识：地图上的方向。

如图1中所示几个圆中，只有AC所在的圆和EF所在的圆为大圆。

对于地理考查来说，一般是考查具有地理意义的大圆，主要包括：赤道、经线圈和晨昏圈，对于这几个大圆上的最短航线方向的判断方法归纳如下：1、两点位于赤道上：向正东或正西。

如图1中C点到A点最短航线方向为向正西。

2、两点位于同一经线圈上：若两点位于同一经线上，则向正南或正北。

如图2中B点到A点最短航线方向为向正北。

若两点经度相对，最短航线则需过较近的极点，北极点附近先向正北再向正南，现极点附近先向正南再向正北。

如图2中E点到C点最短航线方向为先向正北再向正南；E点到D点最短航线方向为先向正南再向正北。

3、两点位于晨昏圈上：若两点均在晨线上或昏线上，则根据地图上的方向判断即可。

如图3中A点到B点最短航线方向为向东南方向。

若两点分别在晨线和昏线上，也需要考虑极点附近的方向问题。

如图3中，A点到D点最短航线的方向为先向西北再向西南；B点到C点最短航线的方向为先向东南再向东北。

经常考查的还有同一纬线上两点的最短航线方向。

若两点在北纬，则最短航线方向需先向北偏再向南偏；若两点在南纬，则最短航线需先向南偏再向北偏。

如图4中，B点到A点最短航线的方向为先向西北再向西南；C点到D点最短航线的方向为先向东南再向东北。

其他任意两点间的最短航线的方向考查较少，而且相对也图1图2 图3图4要容易一些，一般就用地图上方向的判断方法判断即可。

例1.图5中ACB 为晨昏线，C 地点在格陵兰岛上。

1.由A 到B 的最短航线是( )A.由A 点出发沿纬线向东到 BB.沿ACDC.沿ADBD.从A 出发过极点再到 B2.飞行方向的变化是________________。

“小地球”系列—高中地理知识点详解（自然地理）《地球与地球仪》拓展延伸八两点间最短航线方向的判断一.最短航线的确定球面上两点间的最短距离为过两点的大圆的劣弧长度。

球面最短距离是一段劣弧，沿劣弧的行进方向即为最短航线，该弧线的确定可分两个步骤进行：确定“大圆”和确定“劣弧”。

1.“大圆”的确定“大圆”即球面两点所在的过球心的平面与球面的交线，如图所示：①在地球仪上，三种情况下“大圆”是确定的：②非赤道的纬线上两点，所在“大圆”具有以下特征：北半球——大圆向北极方向倾斜；南半球——大圆向南极方向倾斜。

【判读1】找出图中的大圆。

【答案】图中3、4为大圆。

2.“劣弧”的确定“劣弧”即两点间的弧度＜180°，如下图中PQ间的劣弧为上侧一段弧，P′Q′间的劣弧为下侧一段弧。

3.沿劣弧的行进方向即为最短航线【判读2】判断图中各点之间是否为最短距离。

【答案】图中AB之间、CD之间为最短距离。

【判读3】通过下图找出甲乙两点之间的最短距离。

【答案】因3所在的圆为大圆，所以3线路为甲乙之间的最短距离。

二.最短航程上方向的判断1.两地经度和等于180°时的最短航程方向的判断经过两点的大圆便是经线圈，过两极点为最短航程，具体又可分为三种情况：（1）同位于北半球，最近航程一定是先向北，过极点后再向南（如图中A到B或B到A）。

（2）同位于南半球，最近航程一定是先向南，过极点后再向北（如图中A到B或B到A）。

（3）两地位于不同半球，这时需要讨论，要看过北极点为劣弧，还是过南极点的为劣弧，确定后选择劣弧路线部分即可。

上图中AB之间的最短航程为先向北，再向南；CD之间的最短航程为先向南，再向北。

2.若两地经度之和不等于180°（此时往往讨论同纬度的两地，不在同纬度、同半球的比较复杂，具体问题具体分析）经过两点的大圆不是经线圈，而与经线圈斜交，最短航程不过两极点。

（1）若同在北半球由A到B的最短航向是先西北，再正西，后西南；由B到A的最短航向是先东北，再正东，后东南。