两点间的最短航线方向问题
- 格式:ppt
- 大小:165.50 KB
- 文档页数:15



经纬网之阿布丰王创作时间:二O二一年七月二十九日----------飞机最短航线问题1、同一经线上的两点,其最短航线就在这条经线上,方向为正南或正北.(如图中A、C两地或B、D两地)2、若两地经度相差180°,且两地不全在赤道上时,经过两地的年夜圆为经线圈,两地最短航线过极点.(1)两地都在北半球,最短航线过北极点.航向为先向正北,再向正南(如图中A、B两地)(2)两地都在南半球,最短航线过南极点.航向为先向正南,再向正北(如图中C、D两地)(3)若一地在南半球,一地在北半球时,比力两地纬度值的年夜小,最短航线经过两地中纬度值较年夜者所在半球的极点.由A到D时,先向南,过南极点,然后向北由B到C时,先向北,过北极点,然后向南3、同一纬线上的两地(经度差不是180°)(1)两地在赤道上,因赤道是年夜圆,则最短航线沿赤道航行即可,方向为向东或向西.(C、D两地)(2)两地不在在赤道上,最短航线的劣弧段向较高纬度凸出.①两地都位于北半球时,最短航线向北凸出.ⅰ往东时:先向西南,再向西北.(由A到B)ⅱ往西时:先向西北,再向西南.(由 B到A )②两地都位于南半球时,最短航线向南凸出.ⅰ往东时:先向西北,再向西南.(由Q到M)ⅱ往西时:先向西南,再向西北.(由M到Q)4、晨昏线上的两点由于晨昏线自己就是一个年夜圆,故在晨昏线上的两点最短航线就是两点之间的最短晨昏线总结:特殊年夜圆---赤道、经线圈、晨昏圈同一纬线上(非赤道、非经线圈)1:若一架飞机从M点起飞,沿最短航线达到P点,则飞机飞行的方向是()A 一直向东B 先西南再西北C 一直向西D 先西北再西南读下图,N为北极点,年夜圆为经线圈,ACB为赤道3假若一架飞机从A飞到B,实际最短的飞行线路是()A 弧ANB B 弧AGBC 弧AMBD 弧ACB4.上图中从D点到E点的最短航线是()A.先西北后西南 B.先西北后西南C.先西南后西北 D.先西南后西北5、最短航线的特殊情况(1)一位置于赤道,另一地不在赤道和极点上①两地经度差≤ 90°时,最短航线方向不变.②两地经度差>90°时,最短航线方向变动.由C到A时方向为向西南由C到F时方向为向西南由C到B时方向为先向西南,然后向西北(2)两地同位于一个半球,而且不在同一条纬线上时,只考虑一种情况:参照同一条纬线上两地最短航线的选取方法E到F的最短航线为A到F最短航线。



经纬网----------飞机最短航线问题1、同一经线上的两点,其最短航线就在这条经线上,方向为正南或正北;如图中A、C两地或B、D两地2、若两地经度相差180°,且两地不全在赤道上时,经过两地的大圆为经线圈,两地最短航线过极点;1两地都在北半球,最短航线过北极点;航向为先向正北,再向正南如图中A、B两地2两地都在南半球,最短航线过南极点;航向为先向正南,再向正北如图中C、D两地3若一地在南半球,一地在北半球时,比较两地纬度值的大小,最短航线经过两地中纬度值较大者所在半球的极点;由A到D时,先向南,过南极点,然后向北由B到C时, 先向北,过北极点,然后向南3、同一纬线上的两地经度差不是180°1两地在赤道上,因赤道是大圆,则最短航线沿赤道航行即可,方向为向东或向西;C、D两地2两地不在在赤道上,最短航线的劣弧段向较高纬度凸出;①两地都位于北半球时,最短航线向北凸出;ⅰ往东时:先向东北,再向东南;由A到Bⅱ往西时:先向西北,再向西南;由 B到A②两地都位于南半球时,最短航线向南凸出;ⅰ往东时:先向东南,再向东北;由Q到Mⅱ往西时:先向西南,再向西北;由M到Q4、晨昏线上的两点由于晨昏线本身就是一个大圆,故在晨昏线上的两点最短航线就是两点之间的最短晨昏线总结:特殊大圆---赤道、经线圈、晨昏圈同一纬线上非赤道、非经线圈1:若一架飞机从M点起飞,沿最短航线到达P点,则飞机飞行的方向是A 一直向东B 先东北再东南C 一直向西D 先东南再东北读下图,N为北极点,大圆为经线圈,ACB为赤道3假若一架飞机从A飞到B,实际最短的飞行线路是A 弧ANB B 弧AGBC 弧AMBD 弧ACB4.上图中从D点到E点的最短航线是A.先西北后西南 B.先东南后东北C.先西南后西北 D.先东北后东南5、最短航线的特殊情况1一地位于赤道,另一地不在赤道和极点上①两地经度差≤ 90°时,最短航线方向不变;②两地经度差> 90°时,最短航线方向变化;由C到A时方向为向东北由C到F时方向为向东北由C到B时方向为先向东北,然后向东南2两地同位于一个半球,并且不在同一条纬线上时,只考虑一种情况:参照同一条纬线上两地最短航线的选取方法E到F的最短航线为 A到F最短航线。



经纬网----- 飞机最短航线问题1、同一经线上的两点,其最短航线就在这条经线上,方向为正南或正北。
(如图中A、C两地或B D两地)2、若两地经度相差180。
,且两地不全在赤道上时,经过两地的大圆为经线圈,两地最短航线过极点。
(1)两地都在北半球,最短航线过北极点。
航向为先向正北,再向正南(如图中A、B两地)(2)两地都在南半球,最短航线过南极点。
航向为先向正南,再向正北(如图中C D两地)(3)若一地在南半球,一地在北半球时,比较两地纬度值的大小,最短航线经过两地中纬度值较大者所在半球的极点。
由A到D时,先向南,过南极点,然后向北由B到C时,先向北,过北极点,然后向南3、同一纬线上的两地(经度差不是180°)(1)两地在赤道上,因赤道是大圆,则最短航线沿赤道航行即可,方向为向东或向西。
(C D两地)(2)两地不在在赤道上,最短航线的劣弧段向较咼纬度凸出。
①两地都位于北半球时,最短航线向北凸出。
i往东时:先向东北,再向东南。
(由A到B)ii往西时:先向西北,再向西南。
(由B到A )②两地都位于南半球时,最短航线向南凸出。
i往东时:先向东南,再向东北。
(由Q到M i往西时:先向西南,再向西北。
(由M到Q)4、晨昏线上的两点由于晨昏线本身就是一个大圆,故在晨昏线上的两点最短航线就是两点之间的最短晨昏线总结:特殊大圆---赤道、经线圈、晨昏圈同一纬线上(非赤道、非经线圈)1若一架飞机从M点起飞,沿最短航线到达P点,则飞机飞行的向是()A一直向东B先东北再东南C一直向西D先东南再东北读下图,N为北极点,大圆为经线圈,ACB为赤道3假若- 架飞机从A飞到B,头际最短的飞行线路疋A弧ANB B弧AGBC弧AMB D弧ACB方4. 上图中从D点到E点的最短航线是()A .先西北后西南B .先东南后东北C.先西南后西北 D .先东北后东南5、最短航线的特殊情况(1)一地位于赤道,另一地不在赤道和极点上①两地经度差冬90。
地球表面上两点间最短距离(航线)方向的确定作者:***来源:《中学政史地·高中文综》2016年第03期在复习经纬网的内容时,地球表面上两点间最短航线方向的确定,是我们的拦路虎。
由于有的同学对这类问题缺乏足够的空间想象能力,只是机械地背一些结论,造成在解这类试题时经常出错。
针对有些同学空间想象能力和数学水平不太高等情况,本文旨在帮助他们全面正确认识地球表面上两点间最短航线方向的确定问题。
地球表面上两点之间的最短航线,指的是两点所在大圆的劣弧。
一、认识大圆过球面上两点的大圆就是经过这两点以地心为圆心的圆。
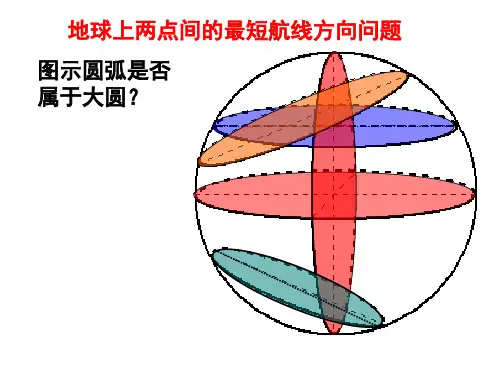
在地球上有三种情况大圆是确定的,如图1中的赤道、经线圈、晨昏圈。
在图2中,很显然,甲、乙、丙所在圆的圆心是地心,其所在的圆就是大圆,其他的圆都不是大圆。
二、确定劣弧大圆上两点间的最短航线或距离就是两点所在大圆的劣弧。
所谓劣弧,即两点间的弧度小于180°。
如图3中的⌒AB和⌒CD都是过大圆的劣弧,而⌒EF虽然是劣弧,但不是大圆上的劣弧。
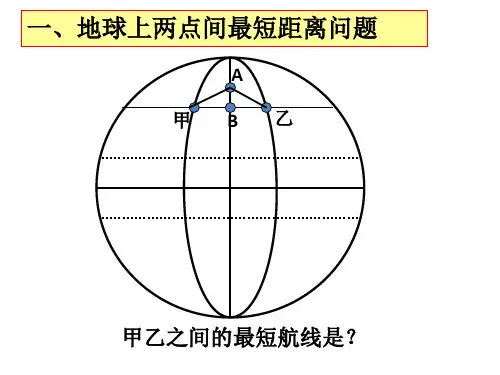
图4中甲和乙之间的弧线,只有最上面的弧是过大圆的劣弧。
三、确定地球上两点间最短航线的方向沿着劣弧的行进方向就是最短航线的方向。
1.两点在同一经线圈上或者在赤道上(1)两点在同一经线上,向正北或向正南走,不转向。
如图5, A到B是向正北走;反之,B到A是向正南走。
(2)两点在两条经线上(经度相对,两点的经度差等于180°),过极点要转向。
如在通过北极点之前,先向正北走,过北极点后转向正南;反之,在通过南极点之前,先向正南走,过南极点后转向正北。
如图6,从A到B先向正北走,过北极点后向正南走;从B 到A是先向正北走,过北极点后向正南走。
(3)两点在赤道上,向正东走或向正西走,不转向。
如图7, A到B是向正东走;反之,B到A是向正西走。
2.两点既不在同一经线上,也不在赤道上地球上任意两点和地心必然确定一个大圆,一定存在一个纬线圈和这个大圆相切,切点即为这个大圆的纬度最高点,若大圆劣弧航线经过切点,则发生转向,转向点为切点;若大圆劣弧航线不经过切点,则不发生转向。
高中地理飞机最短航线题在高中地理学习中,我们经常会遇到关于航线的问题。
其中一个经典的问题就是如何确定飞机的最短航线。
本文将介绍如何解决这个问题,并探讨其中的原理和应用。
首先,我们需要了解什么是最短航线。
最短航线是指两个地点之间的最短距离,通常用直线距离来表示。
然而,在实际情况中,由于地球是一个球体,直线距离并不是最短航线。
这是因为飞机在飞行过程中需要考虑地球的曲率,以及飞行高度的限制。
为了确定最短航线,我们需要使用一个叫做大圆航线的概念。
大圆航线是指连接两个地点的地球表面上的最短路径,它是一个圆周上的一段弧线。
在地理学中,大圆航线被广泛应用于航空和航海导航中。
那么,如何确定飞机的最短航线呢?首先,我们需要知道起点和终点的经纬度坐标。
然后,我们可以使用球面三角学的知识来计算大圆航线的长度和方向。
球面三角学是一种研究球面上的三角形的数学学科,它可以帮助我们解决地球表面上的航线问题。
在计算最短航线时,我们需要使用一些基本的公式和方法。
其中一个重要的公式是球面三角形的余弦定理。
根据余弦定理,我们可以计算出两个地点之间的角度,然后通过这个角度来确定大圆航线的长度。
除了长度,我们还需要确定大圆航线的方向。
在球面三角学中,方向通常用方位角来表示。
方位角是指从一个地点到另一个地点的方向,它是以北为参考的角度。
通过计算方位角,我们可以确定飞机应该朝着哪个方向飞行,以达到最短航线。
最后,我们需要考虑飞行高度的限制。
飞机在飞行过程中需要避开地球表面上的障碍物,如山脉和建筑物。
因此,我们需要根据飞机的高度限制来确定最短航线的可行性。
综上所述,确定飞机的最短航线需要使用球面三角学的知识和相关公式。
通过计算大圆航线的长度和方向,我们可以找到飞机飞行的最短路径。
这对于航空和航海导航来说非常重要,可以帮助飞机和船只节省时间和燃料。
在高中地理学习中,我们经常会遇到飞机最短航线的题目。
通过掌握球面三角学的基本原理和计算方法,我们可以轻松解决这类问题。
例谈地球表面两点之间的最短航线问题地球是一个两极部位略扁的不规则球体,但在讨论两点之间的最短航线时,一般近似地认为地球是一个正球体,即在地球表面上两地之间的最短距离(或航线)应指的是经过这两点的球大圆在这两点间的一段劣弧长度,这个圆的圆心必须经过球心(即地心)。
在中学地理应试中主要有以下几种情况。
1.晨昏线上两点之间的最短距离是该晨昏线上两点之间的劣弧部分。
如图1右图中的的阴影部分为黑夜,GH之间的最短航线是沿着晨昏线的劣弧走:先东南,再向正东,后东北,即经过GMH,而不是GYH。
2.赤道上两点之间的最短距离是赤道上两点之间的劣弧部分。
如图1左图中的AB之间的最短航线:A到B走为正东或B到A走为正西。
3.经线上两点之间的最短距离是该经线上两点之间劣弧部分。
如图1左图中的CD之间的最短航线:C到D为正北或D到A为正南。
4.若两地间的经度差等于180°,则经过两点的大圆一定是经线圈。
这两点间的最短航程须经过极点,其结果只能是先正北后正南或先正南后正北。
⑴同位于北半球的两点,最短航线必须经过北极点,其航行方向一定是先向正北,过北极点后再向正南。
如图1左图中的EF之间的最短航线为先正北后正南,即经过ENF三个点的经线圈的劣弧线,而不是沿EF的纬线走。
⑵同位于南半球的两点,最短航线必须经过南极点,其航行方向一定是先向正南,过北极点后再向正北。
⑶两地位于不同半球时,这时需要考虑是经过北极点为劣弧,还是经过南极点为劣弧,然后再确定最短航程的走向。
如图1左图中的E点到X点的最短航线为先正北后正南,即经过经线圈的ENFX 四个点的劣弧线;而不是先正南后正北,即不是经过经线圈的ESX三个点弧线。
注意:上述四种情况中赤道、经线、经线圈、晨昏线都是大圆或大圆的一部分,故直接可截取球面距离。
5.若两地经度差不等于180°,则过两地的大圆不是经线圈,而是与经线圈斜交,其最短航线不经过极点,具体分两种情况。