0507转角位移方程(力学)
- 格式:ppt
- 大小:787.50 KB
- 文档页数:24

已知 y θ = TT TRRT RR f m , (1) θ=T*y; (2)T 为转换矩阵因为H=1/(-ω2*M+j*ω*C+K ),其中M,C,K 都为是对称矩阵,所以H 为对称矩阵,即H=TT TR RT RR =H T TR=RT T (3)将(2)代入(1)得RT*f+RR*m=T*(TT*f+TR*m) (4)由分配律可得RT=T*TT (5)RR=T*TR (6)在一个多自由度系统中TT= TT 11…TT 1n ⋮⋱⋮TT n1…TT nn (7) TR= TR 11…TR 1n ⋮⋱⋮TR n1…TR nn (8) RT= RT 11…RT 1n ⋮⋱⋮RT n1…RT nn(9) RR= RR 11…RR 1n ⋮⋱⋮RR n1…RR nn (10) 且TT=TT T , RR=RR T (11)由(7)得TT ij =E i *TT*E j T (12)E i , E j 分别表示第i 或j 个元素为1,其他元素为0的一维行向量,且1≤i,j ≤n ,以下相同 由(3),(5),(9),(11)得TR ij =RT ji = TT 1i …TT ji …TT ni ∗T j T = TT i1…TT ij …TT in *T j T = E i *TT*T j T (13) T i , T j ——第i,j 点的转换矩阵E i , E j ——第i 或j 个元素为1,其他元素为0的一维行向量,且1≤i,j ≤n ,以下相同由(5),(7)得RT ij = RT i1…RT ij …RT in *E j T =T i *TT*E j T (14)由(3),(6),(11)得RR ij =RR ji = TR 1i …TR ji …TR ni *T j T = RT i1…RT i2…RT in *T j T=T i *TT*T j T (15)由(12),(14)得 [TT ij RT ij ]= [E i T i] *TT*E j T (16)由(13)(15)得 [TR ij RR ij ]= [E i T i] *TT*T j T (17) 将(16),(17)联立得H ij = TT ij TR ij RT ij RR ij =[E i T i ] *TT*[E j T T j T ]= [E i T i ] *TT* E j T j T。
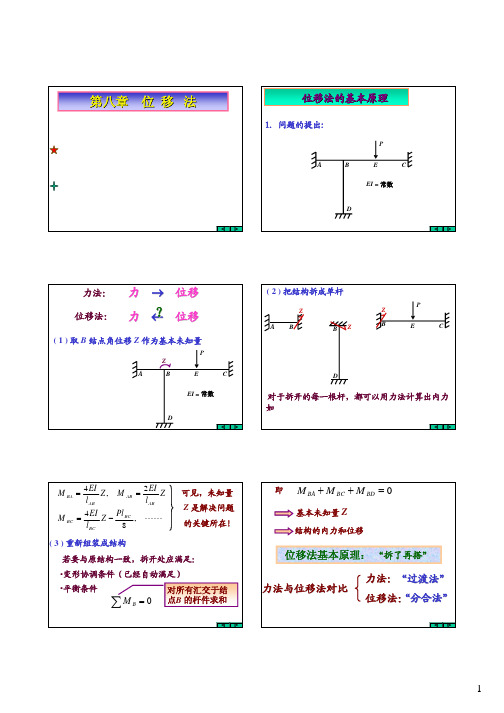
第八章位移法§8-1 位移法的基本原理对所有汇交于结点B 的杆件求和结点独立角位移=位移未知的刚结点数目n= 6独立结点位移为5 ?n= 2n= 4n= 7n= 4n= 1 n= 7n= 3n= 4 (8)(10)n = 3§8-2等截面直杆的转角位移方程固梁:由于荷载和温度变化引起的杆端弯矩,称为固端弯矩。
F BAM ,∆BAM ,由于支座移动引起的杆端弯矩转角位移方程( 刚度方程)Slope-Deflection (Stiffness) Equationil 22FAB AB A AB M li i M +∆−=33ϕAB1il由位移引起的杆端内力, 称为“形常数(shape constant)⎪⎪⎩⎨=B BA i M 4ϕ1,2,3,4;9,10,11,12;17,18,19,20.基本结构§8-3 位移法的典型方程1=R 02=R 基本体系⎩⎨⎧=++==++=00222212112111P P R R R R R R R R ⎩⎨⎧=++=++0022221211212111P P R Z r Z r R Z r Z r 量位移法典型方程二个未知典型方程的物理意义:原结构静力平衡,即基本结构在各结点位移和荷载等外因的共同作用下,每一个附加联系中的附加反力矩或附加反力都应等于零。
对具有n 个独立结点位移的结构,典型方程为:、副系数和自由项ii r ij r ⎪⎪⎩⎪⎪⎨⎧=++⋅⋅⋅++⋅⋅⋅⋅⋅⋅=++⋅⋅⋅++=++⋅⋅⋅++00022112222212111212111nP n nn n n P n n P n n R Z r Z r Z r R Z r Z r Z r R Z r Z r Z r552⎩i。

第3卷第10期2017年10月黑龙江水利Heilongjiang Water ResourcesVol.3,No.10Oct. ,2017用位移法中“典型方程、转角位移方程”的观点进行弯矩分配的解释陈百鸣(富裕县水务局,黑龙江富裕161200)摘要:针对结构力学位移法中典型方程与转角位移方程的应用,根据长期的实践经验和体会,分析概括了位移 法解决超静定结构的基本途径、典型方程的物理意义,以及弯矩分配计算等基本概念,最后给出了在位移法典型 方程解释弯矩分配法中的弯矩分配过程和位移法“转角位移方程”弯矩分配中力矩传递过程的解释。
关键词:位移法;转角位移方程;超静定结构;弯矩分配中图分类号:TU501; TB301 文献标志码:A文章编号:2096-0506(2017)10-0052-041位移法的基本途径对于力法解决超静定结构需要联立多元一次 方程组,计算之复杂性是显而易见的,特别是用 力法计算较复杂的刚架时尤为繁琐,往往要联立 六元以上方程组。
这样就迫使我们寻求新的途径 解决计算这一新课题,在认识解决一项新课题之 前,总是设法寻求一个解决问题的新途径,在这 里,联想力法的思想方法就是遵循从已知到未知 的过程,就是把新课题经过一系列的假定转化为 老问题,进而解决。
在力法处理超静定结构时,是将复杂的超静定结构去掉多余联系后变为静定 结构来处理,那么对于较复杂的刚架来讲,究竟 采取什么样的途径是仍需要解决的问题,我们知 道超静定刚架是由若干个两端可转动的固定端单 跨超静定梁[1](这与实际工程中单跨超静定是不符 的,为了寻求解决问题的途径做这样的假定)所组 成的,采取各个击破的办法分别计算每个单独杆 件的端内力,再组合起来便为刚架整体结构的内 力值。
那么这个单独杆件的端内力又如何计算呢? 对于超静定结构的内力不仅与外荷载有关,而且 还与其形变有关,整体结构的形变引起整体结构 的内力,经过分析得出关系式(1)、式(2),即单 独杆件的端内力与其形变存在下列关系:Ma b =—+2i i2Q a+Q i,—3A/L)(1)M ba =—Mia +2i(2Q b+Q a—3A/L)(2)式中:Q为杆件a端轴线的转角;Q为杆件6端 轴线的转角;Ma6、M6a分别是假想的单跨超静定 梁两端的杆端力矩;M^、A C分别假想的单跨超 静定梁在外力作用下两杆端加以约束的约束力矩,也称固端力矩。

转角位移方程
转角位移方程是一种物理学原理,它能够更有效地描述物体的变动轨迹。
它是由法国物理学家拉瓦锡(LavalVignac)于1776年发明的。
该方程式在曲线求解、向量分析以及机械动作领域服务于科学家。
转角位移公式可以用于描述以点A和B为支点的曲线轨迹,其具体形式是:
V= r [(1-cosα) + (α-sinα)]
其中,V是曲线沿着点A到点B移动的位移量;r是点A到点B 的距离;α是点A和点B之间的夹角,在0~2PI范围内。
转角位移方程有许多应用,其中之一就是在空间的动态研究中。
它可以描述物体从一维运动到二维运动过程中角度的变化。
例如,在一个空间环境中,对于一个物体沿着曲线的行走的情况,转角位移方程可以用来计算该物体沿着曲线行走的总位移量。
另外,转角位移方程也可以用于电机和其他机械产品的运动模拟,以及三维图形处理中的转换计算量的增加。
转角位移方程有其优越性,但存在一些缺点,例如它会复杂化计算量,从而增加程序的运行时间,同时,也会减少程序的效率。
此外,转角位移方程也需要大量的计算量来完成,因此,普通的计算机系统可能无法在短时间内完成。
总之,转角位移方程是一种有用的物理学原理,可以更有效地描述物体的变动轨迹。
虽然它存在一些缺点,但它仍然为科学研究和工程应用提供了重要的依据。

转角位移方程
其中,x表示物体所在的位置。
v0表示物体的初始速度;t表示时间;a表示加速度。
由于加速度是恒定的,可以将时间划分为固定的区间,通过计算每个时间段的位移,可以得到物体实际运动轨迹。
例如,假设方程中加速度为10m/s^2,初始速度为2m/s,则在
t=1s时,物体的位移为2*1+1/2*10*1^2 = 12m。
转角位移方程也可以用于研究物体的加速度。
可以将时间划分为若干等分,通过记录每个时间点物体的位移,可以得到物体的加速度。
例如,如果位移x1 = 12m,x2 = 18m,t1 = 1s,t2 = 2s,则物体的加速度为(18-12)/(2-1) = 6m/s^2。
除此之外,转角位移方程还可以用于计算物体的动能和势能。
物体的动能与物体的速度和质量有关,而势能则与物体的位置有关。
可以将时间划分为若干等分,通过计算每个时间点物体的位移和速度,可以得到物体的动能和势能。
转角位移方程是一种重要的物理模型,它可以用来计算物体的位移、速度、加速度、动能和势能等,为物理研究提供了重要的理论依据。
它的应用涉及到机械、电子、航空等许多领域,是工程技术人员必须要掌握的基本知识之一。
只有深入理解转角位移方程,才能在实际工程中正确应用它,为工程技术人员提供有效的理论指导。
- 1 -。

位移法典型方程根据(实用版)目录1.位移法的基本概念2.位移法的典型方程3.位移法的应用实例4.位移法的优缺点分析正文一、位移法的基本概念位移法是一种求解固体力学问题的数值方法,主要通过计算物体在受力作用下的位移来研究其内部应力和应变分布。
位移法基于弹性力学的基本原理,适用于求解各种复杂的固体力学问题,如梁、板、壳等结构在受力作用下的变形和内部应力分布。
二、位移法的典型方程位移法的典型方程是根据弹性力学原理推导得到的。
以一维简支梁为例,当梁受到均布荷载作用时,其位移法的典型方程为:挠度公式:f(x) = q(x-x0)/8EI弯矩公式:M(x) = EI*(f"(x)-qx)/2其中,f(x) 表示梁在 x 处的挠度,M(x) 表示梁在 x 处的弯矩,E 为材料的弹性模量,I 为梁的惯性矩,q 为均布荷载,x0 为梁的支点,f"(x) 为挠度的一阶导数。
三、位移法的应用实例位移法广泛应用于各种固体力学问题的求解,如梁、板、壳等结构在受力作用下的变形和内部应力分布。
例如,在求解简支梁在均布荷载作用下的挠度和弯矩时,可以采用位移法进行计算。
四、位移法的优缺点分析1.优点:位移法求解固体力学问题时,可以通过计算物体的位移来直接得到其内部应力和应变分布,避免了传统力学方法中的繁琐计算过程。
此外,位移法适用于各种复杂的固体力学问题,具有较强的通用性。
2.缺点:位移法的求解过程涉及到较高阶的微分方程,计算过程较为复杂。
在某些特殊情况下,位移法的求解结果可能不如其他方法准确。
总之,位移法作为一种求解固体力学问题的数值方法,具有广泛的应用前景。