结构力学[第八章矩阵位移法]课程复习

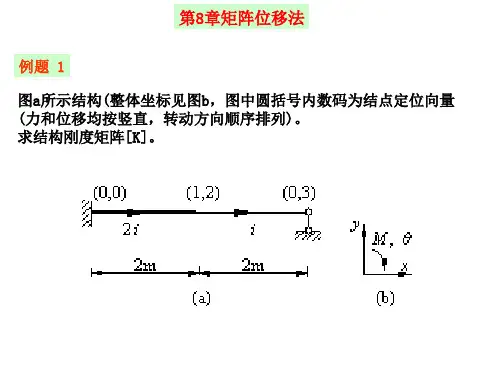
第8章 矩阵位移法 ♍♦♐ 制作同济大学教材笔记(本章答案陆续上传中)一、知识要点： 1.结构坐标系一般采用右手坐标系，记为xoy 。

此时，结点位移和结点力均取与结构坐标系方向一致为正，其中结点的角位移和结点力矩按右手法则均取逆时针方向为正。

2.局部坐标系主要注意α角的定义，看如下图示即明白。

yxoijexyα3.桁架单元刚度方程000000000000eeexi i yi i xj j yj j EAEA F u l lF v EA EAF u l l F v ⎛⎫-⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎪= ⎪ ⎪⎪ ⎪ ⎪-⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎪⎝⎭桁架结构变换矩阵Tcos sin 00sin cos 0000cos sin 00sin cos T αααααααα⎛⎫⎪-⎪= ⎪ ⎪-⎝⎭桁架在结构坐标系下的单元刚度矩阵22222222ee c sc c sc sc s sc s EA k l c sc c sc sc s sc s ⎛⎫-- ⎪-- ⎪=⎪-- ⎪⎪--⎝⎭4.刚架单元刚度方程32322232322212612664621261266264eeeyi i i i yj j j j EIEI EI EI l l l l F v EI EI EI EI M l l l l EI EI EI EI F v l l l l M EI EI EI EI l l l l θθ⎛⎫- ⎪⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪ ⎪--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎪⎪-⎝⎭5.受轴向力作用的一般刚架单元刚度方程32322232322200001261260064620000001261260062640eexi i yi i i i xj j yj j EAEA ll EI EIEI EI F u l l l l F v EI EI EI EI M l l l l EA EA F u l l F v EIEI EI EI M l l l l EI EI EI EI l lllθ⎛⎫- ⎪⎪ ⎪⎛⎫- ⎪ ⎪⎪ ⎪ ⎪ ⎪- ⎪ ⎪=⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--- ⎪⎝⎭⎪ ⎪- ⎪⎝⎭ej j ⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭一般刚架单元刚度方程的坐标变换矩阵Tcos sin 0000sin cos 0000001000000cos sin 0000sin cos 0001T αααααααα⎛⎫⎪- ⎪ ⎪=⎪ ⎪ ⎪- ⎪ ⎪⎝⎭结构坐标系下的一般刚架单元刚度矩阵e k12412423523545645612412423523545645622ea a a a a a a a a a a a a a a a a a k a a a a a a a a a a a a a a a a a a --⎛-- --=---- ---- --⎝6.为什么已知杆端位移能求得单元的唯一杆端力，而已知杆端力却无法唯一确定杆端位移这是因为支座位移条件不已知，可能相差一个刚体位移，即位移的绝对值不同。

习 题8-1 试说出单元刚度矩阵的物理意义及其性质与特点。

8-2 试说出空间桁架和刚架单元刚度矩阵的阶数。

8-3 试分别采用后处理法和先处理法列出图示梁的结构刚度矩阵。

(a)解：（a ）用后处理法计算 （1）结构标识（2）建立结点位移向量，结点力向量[]T44332211 θνθνθνθν=∆[]Ty M F M F M F M F F 4y43y32y211 =θ（3）计算单元刚度矩阵⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=2222322211211462661261226466126122EI 21 l l -l l l -l -l l -l l l l - l k k k k k ①①①①①⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=222233332232223 33 6 3632336 362EI 21 l l - l l l - l -l l -l l l -l l k k k k k ②②②②②lll⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡=222234443343323 33 6 3632336 362EI 2 1 l l - l l l - l -l l -l l l -l l k k k k k ③③③③③（4）总刚度矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡++=222222222234443343333322322222112112 3300003 6 3 6 000 03403003601236000 0 3632600 363186120000 26460 0 0 06126122EI 0 0 00 0 0 4 3 2 1 4 3 2 1 l l -l l l - l - - l l -l l l l - l - - l l -l l -l l l l - -l -- l l -l l l l - l k k k k k k k k k k k k k ③③③③②②②②①①①①θ （5）建立结构刚度矩阵支座位移边界条件[][]00004311 θ θ θν=将总刚度矩阵中对应上述边界位移行列删除，得刚度结构矩阵。

结构力学概念复习矩阵位移法复习1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。

答案：正确2、单元刚度矩阵均具有对称性和奇异性。

答案：错误，是否考虑边界条件3、局部坐标系与整体坐标系之间的坐标变换矩阵T是正交矩阵。

答案：正确4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。

答案：错误，反映了整体结构的变形协调条件和平衡条件5、在直接刚度法的先处理法中，定位向量的物理意义是变形连续条件和位移边界条件。

答案：正确6、图示结构用矩阵位移法计算时（计轴向变形）未知量数目为8个。

答案：正确7、等效结点荷载数值等于汇交于该结点所有固端力的代数和。

答案：错误，计算反号8、矩阵位移法中，等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。

答案：正确9、矩阵位移法既能计算超静定结构，也能计算静定结构。

答案：正确 10、矩阵位移法中，结构在等效结点荷载作用下的内力与与结构在原有荷载作用下的内力相同。

答案：错误11、已知杆端力向量就可以通过单元刚度矩阵计算出杆端位移向量。

答案：错误12、已知杆端位移向量就可以通过单元刚度矩阵计算出杆端力向量。

答案：正确13、单元刚度矩阵是单元的固有特性，与坐标选取无关。

答案：错误14、整体坐标系中的杆端力，依次是N、Q、M。

答案：错误15、结构的整体刚度矩阵可直接由整体坐标下的单元刚度的元素按“对号入座”的方式集成。

答案：正确动力分析复习1、结构计算中，大小、方向随时间变化的荷载必须按动荷载考虑。

答案：错误2、单自由度体系其它参数不变，只有刚度EI增大到原来的2倍，则周期比原来的周期减小1/2。

答案：错误3、结构在动力荷载作用下，其动内力与动位移仅与动力荷载的变化规律有关。

答案：错误4、由于阻尼的存在，任何振动都不会长期继续下去。

答案：错误5、图示刚架不计分布质量和直杆轴向变形，图a刚架的振动自由度为2，图b刚架的振动自由度也为2。

答案：正确(a)(b)6、设 W、Wd分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率，两者的关系为W=Wd 答案：错误7、单体中某个杆件刚度减小时，结构自振周期不一定都增大。