几何组成分析习题
- 格式:doc
- 大小:118.00 KB
- 文档页数:2


7 .图题1- 3 (a)所示体系,几何组成分析试题一、是非判断:1.在一个平面体系上增加二元体不会改变体系的计算自由度。
( )2.若平面体系的计算自山度W= 0,则该体系为无多余约束的几何不变体系或瞬变体系,而不可能为常变体系。
( )3.平面较接杆件体系的计算自由度W^2j-b-r,式中/表不体系中的单较的个数。
( )4.若平面体系的计算自由度W<0,则该体系不可能是静定结构。
( )5 .图题l-l(a)所示体系去掉二元体AB、AC后,成为图(b)的几何可变体系,故原体图(a)系为几何可变体系。
( )6 .图题l-2(a)所示体系依次去掉二元体AB、AC及BD、BE后,成为图(b)所示体系,故原体系是无多余约束的几何不变体系。
( )题1-2图题1-3图8.图题1-4 (a)所示体系,依结点1、2、3、4的顺序去掉4个二元体后,就只剩下地基,故原体系是无多余约束的几何不变体系。
( )二、填空1.如图2-1所示体系为具有 ______________ 个多余约束的几何不变体系。
2.如图2-2所示体系为______________ 体系。
3.如图2-3所示体系为______________ 体系。
III题2-3题2-4题2-5题2-6Az——C)——R4 .如图2-4所示刚片I 、II 、III 由较力及链杆1、2、3、4连接,若较力与及链杆1共线,则所 组成体系为 _____________ 体系;若較〃与及链杆1不共线,则所组成体系为 ________________ 体系。
5 .如图2-5所示体系为 __________ 体系。
------------ 9Q O Q O题2-7图6 .如图2-6所示体系为 __________ 体系。
7 .如图2-7所示体系为 __________ 体系。
8 .如图2-8所示体系为 __________ 体系。
三〜五、试对图三〜五所示体系进行几何组成分析。

一、对图示体系进行几何组成分析。
(10分)解:折杆ABC 、CDE 与BD 形成刚片I ,为几何不变体系且无多余约束。
(5分)刚片I 与地面由4链杆相连,整个结构为几何不变且有1个多余约束。
(5分)二、计算图示静定桁架的支座反力及1、2杆的轴力。
(14分)解:求支座反力)(2),(6),(2↑=↑=←=kN R kN Y kN X B A A (6分)求1、2杆的轴力截面法: )(520251011拉kN N N Y ==+⨯-=∑ (4分) 取E 结点: )(240214022压kN N N Y -==⨯--=∑(4分)三、P = 1在图示静定多跨梁ABCD 上移动。
(1)作截面E 的剪力影响线;(2)画出使Q E 达最大值和最小值时可动均布荷载的最不利布置;(3)当可动均布荷载q = 20 kN/m 时,求Q Emax 值。
(16分)(1) Q E 影响线见图(5分)(2)Q Emax 的最不利位置 (3分)Q Emin 的最不利位置 (3分)(3)kN q Q E 38)5332152521(20max =⨯⨯+⨯⨯⨯=∑=+ω(5分)四、用力法计算图示刚架,画M 图。
EI 为常数(20分)解:1、一次超静定结构,基本体系和基本未知量,如图 (2分)A B CDE 0.4 0.6+ -+0.4C ED2、列力法方程 01111=∆+P X δ (1分)3、作图和P M M ___1 (6分) 4、计算系数、自由项EI 14411=δ (3分) EIP 8101-=∆ (3分)5、解方程 kN X 625.51= (1分)6、作M 图 (4分)五、用位移法计算图示刚架,并作M 图。
各杆EI 为常数。
(20分)解:1、以刚结点角位移为基本未知量,得基本体系 (2分);2、绘1M P M 图(图略) (6分)3、列位移法典型方程: 01111=+P F z k (2分)(4分)图(kNm )33.75六、用力矩分配法绘制图示连续梁的弯矩图。


一、对图示体系进行几何组成分析。
(10分)解:折杆ABC 、CDE 与BD 形成刚片I ,为几何不变体系且无多余约束。
(5分)刚片I 与地面由4链杆相连,整个结构为几何不变且有1个多余约束。
(5分)二、计算图示静定桁架的支座反力及1、2杆的轴力。
(14分)解:求支座反力)(2),(6),(2↑=↑=←=kN R kN Y kN X B A A (6分)求1、2杆的轴力截面法: )(52025111拉kN N N Y ==+⨯-=∑ (4分) 取E 结点: )(240214022压kN N N Y -==⨯--=∑(4分)三、P = 1在图示静定多跨梁ABCD 上移动。
(1)作截面E 的剪力影响线;(2)画出使Q E 达最大值和最小值时可动均布荷载的最不利布置;(3)当可动均布荷载q = 20 kN/m 时,求Q Emax 值。
(16分)(1) Q E 影响线见图(5分)(2)Q Emax 的最不利位置 (3分)Q Emin 的最不利位置 (3分)(3)kN q Q E 38)5332152521(20max =⨯⨯+⨯⨯⨯=∑=+ω(5分) 四、用力法计算图示刚架,画M 图。
EI 为常数(20分)解:1、一次超静定结构,基本体系和基本未知量,如图 (2分)A B C D E0.40.6 +-+0.4 C C D2、列力法方程 01111=∆+P X δ (1分)3、作图和P M M ___1 (6分)4、计算系数、自由项 EI 14411=δ (3分) EIP 8101-=∆ (3分) 5、解方程 kN X 625.51= (1分)6、作M 图 (4分)五、用位移法计算图示刚架,并作M 图。
各杆EI 为常数。
(20分)解:1、以刚结点角位移为基本未知量,得基本体系 (2分);2、绘1M P M 图(图略) (6分)3、列位移法典型方程: 01111=+P F z k (2分)(4分)图(kNm )33.75六、用力矩分配法绘制图示连续梁的弯矩图。

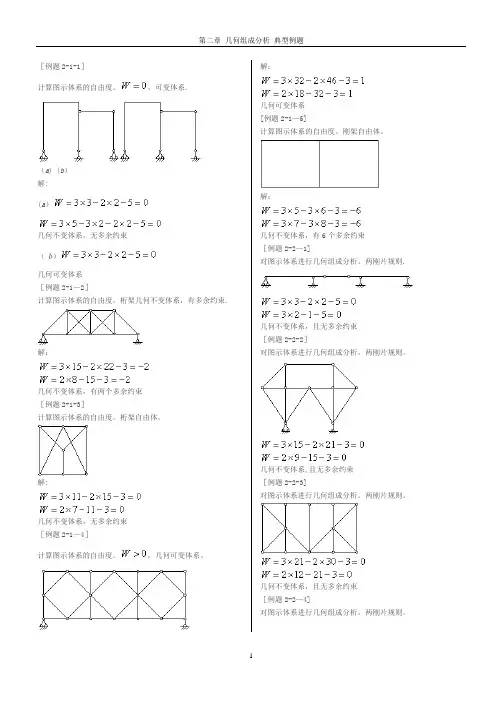
[例题2-1-1]计算图示体系的自由度。
,可变体系.(a) (b)解:(a)几何不变体系,无多余约束(b )几何可变体系[例题2-1—2]计算图示体系的自由度。
桁架几何不变体系,有多余约束. 解:几何不变体系,有两个多余约束[例题2-1-3]计算图示体系的自由度。
桁架自由体。
解:几何不变体系,无多余约束[例题2-1—4]计算图示体系的自由度。
,几何可变体系。
解:几何可变体系[例题2-1—5]计算图示体系的自由度。
刚架自由体。
解:几何不变体系,有6个多余约束[例题2-2—1]对图示体系进行几何组成分析。
两刚片规则.几何不变体系,且无多余约束[例题2-2-2]对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,且无多余约束[例题2-2-3]对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,且无多余约束[例题2-2—4]对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,有一个多余约束[例题2—2—5]对图示体系进行几何组成分析.二元体规则.几何不变体系,且无多余约束[例题2-2—6]对图示体系进行几何组成分析.两刚片规则,三刚片规则.几何不变体系,且无多余约束[例题2-2-7]对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束[例题2-2-8]对图示体系进行几何组成分析.三刚片规则.几何不变体系,且无多余约束[例题2-3-1]对图示体系进行几何组成分析.两刚片规则。
几何瞬变体系[例题2—3—2]对图示体系进行几何组成分析。
两刚片规则。
几何瞬变体系[例题2-3-3]对图示体系进行几何组成分析。
三刚片规则。
几何瞬变体系[例题2—3-4]对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束[例题2-3-5]对图示体系进行几何组成分析.三刚片规则.几何不变体系,且无多余约束[例题2-3—6]对图示体系进行几何组成分析。
二元体规则,三刚片规则.几何瞬变体系[例题2-3-7]对图示体系进行几何组成分析。

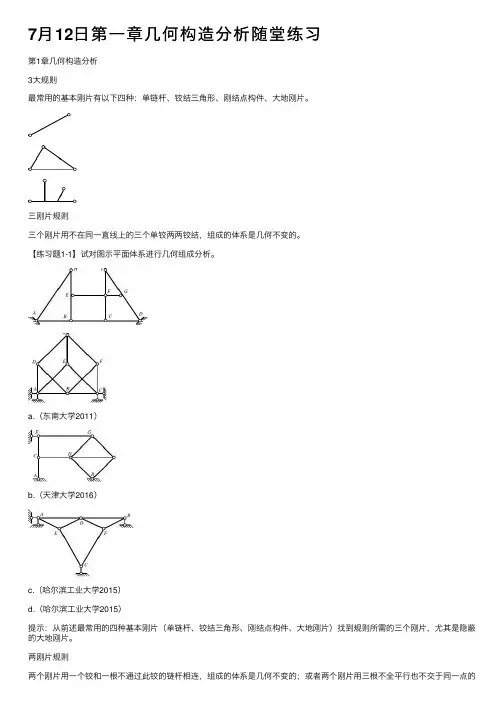
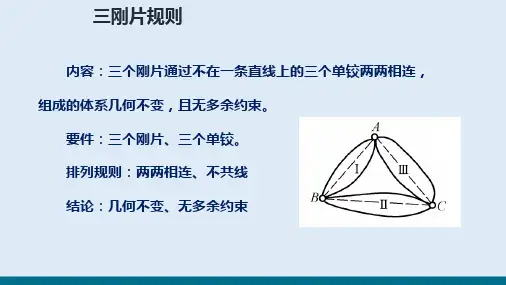
7⽉12⽇第⼀章⼏何构造分析随堂练习第1章⼏何构造分析3⼤规则最常⽤的基本刚⽚有以下四种:单链杆、铰结三⾓形、刚结点构件、⼤地刚⽚。
三刚⽚规则三个刚⽚⽤不在同⼀直线上的三个单铰两两铰结,组成的体系是⼏何不变的。
【练习题1-1】试对图⽰平⾯体系进⾏⼏何组成分析。
a.(东南⼤学2011)b.(天津⼤学2016)c.(哈尔滨⼯业⼤学2015)d.(哈尔滨⼯业⼤学2015)提⽰:从前述最常⽤的四种基本刚⽚(单链杆、铰结三⾓形、刚结点构件、⼤地刚⽚)找到规则所需的三个刚⽚,尤其是隐蔽的⼤地刚⽚。
两刚⽚规则两个刚⽚⽤⼀个铰和⼀根不通过此铰的链杆相连,组成的体系是⼏何不变的;或者两个刚⽚⽤三根不全平⾏也不交于同⼀点的链杆相连,为⼏何不变体系。
【练习题1-2】试对图⽰平⾯体系进⾏⼏何组成分析。
⼆元体规则⼆元体:两个刚⽚与⼀个体系间只⽤三个不在⼀直线上的铰两两相连,则两个刚⽚称为⼆元体。
最简单常见的⼆元体是指由两根不在同⼀直线上的链杆连接⼀个新结点的装置。
⼆元体本质上还是在原⼏何体系上构造出⼀个新的铰结三⾓形,因此本质上就是铰结三⾓形。
在⼀个体系上增加或拆除⼆元体,不会改变原有体系的⼏何构造性质。
值得注意的是:构成⼆元体的两根链杆不⼀定是直杆,只要是刚⽚就⾏。
【练习题1-3】试对图⽰平⾯体系进⾏⼏何组成分析。
a.(中南⼤学2012)b.(东南2010)c.(东南2010)d.(北京⼯业⼤学2011)e.(东南⼤学2011)提⽰:找出⼆元体并依次去掉⼆元体,最后分析体系剩余部分的⼏何构造特性。
记住,⼆元体不⼀定得是直杆组成。
2⼤可变体系1. 瞬变与常变的区分瞬变体系与常变体系的两个判定规则:微⼩变形规则让体系发⽣微⼩变形,若三铰依然在同⼀直线上,则是常变体系,不在同⼀直线上,则是瞬变体系。
平⾏等长规则(特别注意平⾏等长的对象是谁)组成⽆穷远铰的两根平⾏链杆与另外两铰的连线等长且始终平⾏(即发⽣微⼩位移后依然平⾏),则为常变体系,否则为瞬变体系。
题15.7试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 2j -6-r=2×8-9-7=0(2)几何组成分析。
首先把三角形ACD和BCE分别看做刚片I和刚片Ⅱ,把基础看做刚片I,则三个刚片用不共线的三个铰A、B、C分别两两相联,组成一个大的刚片。
在这个大的刚片上依次增加二元体12、DGF、CHG、EIH、IJ3。
最后得知整个体系为几何不变,且无多余约束。
题15.8试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 3m - 2h -r=3×6-2×7—4=0(2)几何组成分析。
刚片AF和AB由不共线的单铰A以及链杆DH相联,构成刚片I,同理可把BICEG部分看做刚片Ⅱ,把基础以及二元体12、34看作刚片I,则刚片I、Ⅱ、Ⅲ由不共线的三个铰F、B、G两两相联,构成几何不变体系,且无多余约束。
题15.9试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 3m - 2h -r=3×14 -2×19 -4一O(2)几何组成分析。
在刚片HD上依次增加二元体DCJ、CBI、BAH构成刚片I,同理可把DMG部分看做刚片Ⅱ,把基础看做刚片I,则刚片I、Ⅱ、Ⅲ由不共线的单铰D,虚铰N、O 相联,构成几何不变体系,且无多余约束。
题15.10试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W-2j—b-r=2×7—11-3一O(2)几何组成分析。
由于AFG部分由基础简支,所以可只分析AFG部分。
可去掉二元体BAC只分析BFGC部分。
把三角形BDF、CEG分别看做附片I和I,刚片I和I由三根平行的链杆相联,因而整个体系为瞬变。
题15.11试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 2j -6-r=2×9-13—5一O(2)几何组成分析。
首先在基础上依次增加二元体12、AE3、AFE、ABF、FI4,成一个大的刚片I。
第一章 平面体系的几何组成分析一、判断题:1、在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
2、图中链杆1和2的交点O 可视为虚铰。
O二、分析题:对下列平面体系进行几何组成分析。
3、 4、CDBCDB5、 6、A CDBEABCDE7、 8、ABCD GE FA BCDEFGHK11、 12、1234513、 14、15、 16、17、 18、1245321、 22、123456781234523、 24、12345625、 26、27、 28、31、32、33、BA CFDE三、在下列体系中添加支承链杆,使之成为无多余约束的几何不变体系。
34、35、第二章 静定结构内力计算一、判断题:1、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图(a)所示结构||M C =0。
aa(a)BCa aAϕ2a2 (b)5、图(b)所示结构支座A 转动ϕ角,M AB = 0, R C = 0。
6、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图(c)所示静定结构,在竖向荷载作用下,AB 是基本部分,BC 是附属部分。
ABC(c)8、图(d)所示结构B 支座反力等于P /2()↑。
(d)9、图(e)所示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB(e)10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
11、图(f)所示桁架有9根零杆。
(f)a a a a(g)12、图(g)所示桁架有:N1=N2=N3= 0。
13、图(h)所示桁架DE杆的内力为零。
a a(h)(i)14、图(i)所示对称桁架在对称荷载作用下,其零杆共有三根。
15、图(j)所示桁架共有三根零杆。
(j)3m3m3m(k)16、图(k)所示结构的零杆有7根。
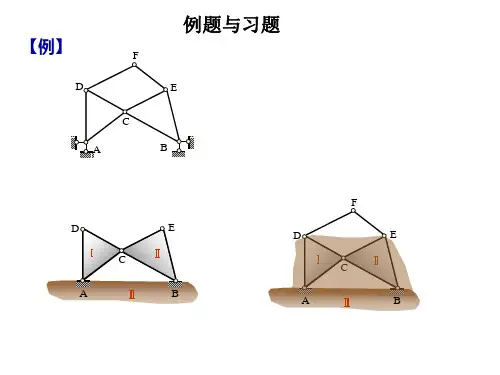
【例2-3】对如图2-18所示体系进行几何组成分析。
图2-18 例2-3图【解】如图2-18(a)所示体系,分别将曲杆AC、曲杆BD及基础当作刚片Ⅰ、Ⅱ及Ⅲ。
其中,刚片Ⅰ、Ⅲ间通过实铰A相连,刚片Ⅱ、Ⅲ间通过实铰B相连,刚片Ⅰ、Ⅱ间通过链杆CD、EF相连(虚铰在其交点O处)。
三刚片间通过两个实铰A、B及一个虚铰O两两相连,这三铰不共线,形成几何不变体系且无多余约束。
如图2-18(b)所示体系,分别以杆CD、杆AB及基础作为三个刚片:Ⅰ、Ⅱ和Ⅲ。
刚片Ⅰ、Ⅱ间通过平行链杆AC、BD相连(虚铰(Ⅰ, Ⅱ)在无穷远处),刚片Ⅰ、Ⅲ间分别通过C、D处的支座链杆相连(虚铰在结点D处),刚片Ⅱ、Ⅲ间分别通过A、B处的支座链杆相连(虚铰在结点A处)。
三刚片间通过两个有限远虚铰(在结点A和D处)及一个无限远处虚铰(Ⅰ, Ⅱ)两两相连,由于两个有限远处虚铰的连线AD,与形成无穷处虚铰的平行链杆(杆AC、BD)不平行,因此形成的是几何不变体系且无多余约束。
如图2-18(c)所示体系,分别以铰结三角形124、铰结三角形237及杆56作为基本刚片:刚片Ⅰ、Ⅱ和Ⅲ。
刚片Ⅰ、Ⅱ间通过实铰2相连,刚片Ⅰ、Ⅲ间通过平行链杆16、45相连,刚片Ⅱ、Ⅲ间通过平行链杆35、67相连,这两对平行链杆形成的虚铰(Ⅰ,Ⅲ)、(Ⅱ,Ⅲ)均位于无穷远处。
这样,三刚片通过三铰两两相连,其中两铰位于无穷远处,由于形成两个无穷远处虚铰的两对平行链杆不互相平行,因此上部体系为无多余约束的几何不变部分。
上部体系再分别通过三个支座链杆与基础相连,按两刚片规则,形成的整个体系为无多余约束的几何不变体系。
如图2-18(d)所示体系,分别以杆15、36及24作为三个基本刚片Ⅰ、Ⅱ和Ⅲ。
刚片Ⅰ、Ⅱ间通过一对平行链杆13、56相连,刚片Ⅰ、Ⅲ间通过一对平行链杆12、54相连,刚片Ⅱ、Ⅲ通过一对平行链杆23、46相连。
三对平行链杆形成的虚铰均在无穷远处,因而形成的上部体系是几何瞬变体系。
几何组成分析
4.图示体系按三刚片法则分析,三铰共线,故为几何瞬变体系。
( )
5.图示体系为几何不变有多余约束。
( )
6.图示体系为几何瞬变。
( )
8.几何可变体系在任何荷载作用下都不能平衡。
( )
9.三个刚片由三个铰相联的体系一定是静定结构。
( )
10.无多余约束的体系一定是静定结构。
( )
二、选择题
1.三个刚片用三个铰两两相互联结而成的体系是:
a.几何不变;
b.几何常变;
c.几何瞬变;
d.几何不变几何常变或几何瞬变。
( )
2.联结三个刚片的铰结点,相当的约束个数为:
a.2个;
b.3个;
c.4个;
d.5个。
( )
3.两个刚片,用三根链杆联结而成的体系是:
a.几何常变;
b.几何不变;
c.几何瞬变;
d.几何不变或几何常变或几何瞬变。
( )
4.图示体系是:
a.几何瞬变有多余约束;
b.几何不变;
c.几何常变;
d.几何瞬变无多余约束。
( )。