第4讲 2-3几何组成分析 习题课

李廉锟《结构力学》（第6版）笔记和课后习题（含考研真题）详解复习笔记【知识框架】节选自识库学习网，如需转载请注明出处【重点难点归纳】一、结构力学的研究对象和任务（见表1-1-1）★★表1-1-1结构力学的研究对象和任务二、荷载的分类（见表1-1-2）★★★荷载是指作用在结构上的主动力。

表1-1-2荷载的分类三、支座和结点的类型★★★★1支座支座是指把结构与基础联系起来的装置，见表1-1-3。

表1-1-3支座的类型2结点结点是指结构中杆件相互联结的位置，见表1-1-4。

表1-1-4结点的类型四、结构的分类★★★1按几何特征分类（见表1-1-5）表1-1-5结构按几何特征分类2按受力特性分类（见表1-1-6）考研真题汇编第1章绪论本章暂未编选名校考研真题。

【更多考研专业课真题可转识库学习网】第2章平面体系的机动分析一、填空题1在平面体系中，联结______的铰称为单铰，联结______的铰称为复铰。

[哈尔滨工业大学2007研]【答案】两个刚片；两个以上的刚片查看答案【解析】根据定义，单铰是指联结两个刚片的一个铰；复铰是指同时联结两个以上刚片的一个铰。

2如图2-1所示体系为有______个多余约束的______体系。

[国防科技大学2007研]图2-1【答案】0；几何不变查看答案【解析】几何组成分析：将AED和DCF分别看作两个刚片，BE和BF可以分别看作两根链杆，再将大地看作一个刚片，此体系可看作通过两个虚铰和一个实铰（三个铰不共线）联结的；根据三刚片规则，可判断出该体系为无多余约束的几何不变体系。

3如图2-2所示体系为有______个多余约束的______体系。

[国防科技大学2004研]图2-2【答案】5；瞬变查看答案【解析】几何组成分析，分析上部结构：将4个组合节点全部变成铰接点，则减少4个多余约束；分析剩余结构，易知该剩余部分为有1个多余约束的几何不变体系，故上部结构为有5个多余约束的几何不变体系。

1、杆系结构中梁、刚架、桁架及拱的分类，是根据结构计算简图来划分的。

(正确)2、定向支座总是存在—个约束反力矩(正确)和一个竖向约束反力。

(错误)3静力和动力荷载的区别，主要是取决于它随时间变化规律、加载速度的快慢。

其定性指标由结构的自振周期来确定。

(正确)4、铰结点的特性是被连杆件在连接处既不能相对移动，(正确)又不能相对转动。

(错误)5、线弹性结构是指其平衡方程是线性的，(正确)变形微小，(正确)且应力与应变之间服从虎克定律。

(正确)1、学习本课程的主要任务是：研究结构在各种外因作用下结构内力与（）计算，荷载作用下的结构反应；研究结构的（）规则和（）形式等问题。

正确答案：位移，动，组成，合理2、支座计算简图可分为刚性支座与弹性支座，其中刚性支座又可分为（）、（）、（）和（）。

正确答案：链杆，固定铰支座，固定支座，滑动支座3、永远作用在结构上的荷载称为固定荷载，暂时作用在结构上的荷载称为（）它包括（）、（）、（）、（）和（）等正确答案：活载，风，雪，人群，车辆，吊车4、刚节点的特性是被连接的杆件载连接处既无（）又不能相对（）；既可传递（），也可传递（）正确答案：移动，转动，力，力矩第二章平面体系的几何构成分析1、图中链杆1和2的交点O可视为虚铰。

（）O正确答案：正确2、两刚片或三刚片组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必须满足的条件。

（）正确答案：正确3、在图示体系中，去掉1-5，3-5，4-5，2-5，四根链杆后，的简支梁12，故该体系具有四个多余约束的几何不变体系。

（）12345正确答案：错误4、几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系，因而可以用作工程结构。

（）正确答案：错误5、图示体系是几何不变体系。

()正确答案：错误2-2几何组成分析1．正确答案：几何不变，且无多余联系。

2．(图中未编号的点为交叉点。

)A B CDEF正确答案：铰接三角形BCD视为刚片I，AE视为刚片II，基础视为刚片III；I、II间用链杆AB、EC构成的虚铰(在C点)相连，I、III间用链杆FB和D处支杆构成的虚铰(在B点)相联，II、III 间由链杆AF和E处支杆构成的虚铰相联3．(图中未画圈的点为交叉点。

第二课时组合的综合应用课堂讲练设计，举一能通类题皿。

有限制条件的组合问题I典例I课外活动小组共13人，其中男生8人，女生5人，并且男、女各指定一名队长，现从中选5人主持某种活动，依下列条件各有多少种选法?(1)只有一名女生3(2)两队长当选；(3)至少有一名队长当选;(4)至多有两名女生当选.［解］(1)一名女生，四名男生，故共有a・Cil=350(种)选法.(2)将两队长作为一类，其他11人作为一类,故共有a・Ch=165(种)选法.(3)至少有一名队长当逸含有两类：有一名队长当选和两名队长都当选.故共有C1-C11+ C心=825(种)选法.或策用间接法：Ch-C和=825(种).(4)至多有两名女生舍有三如有两名女生，只有一名女生，没有女生.故共有C&CS+ aa+ci=966(种)选法.Ii有限制条件的抽(选)取问题，主要有两类：>•!一是“含”与“不含”问题，其解法常用直接分步法，即“含”的先取出.“不含”I:的可把所指元素去掉再取，分步计数；;二是“至多”“至少〃问题，其解法常有两种解决思路：一是直接分类法，但要注Ii意分类要不重不漏；二是间接法，注意找准对立面，确保不重不漏,L_________.________________.________________....._____________....._____________.................................................................J 【活学活用］有，个不同的球，】个不同的盒子，把球全部放入盒内.(1)恰有1个空盒，有几种放法？(2)恰有2个盒子不放球，有几种放法？解：⑴先从4个小球中取2个放在一起，有C3种不同的取法，再把取出的2个小球与另外2个小球看成三堆，并分别放入4个尘子中的3个盒子里，有A］种放法，根据分步来法计数原理，共有CiM=144(种)不同的放法.(2)恰有2个盒子不放球，也就是把4个不同的小球只放入2个盒子中.有两妾放法：第一如1个盒子放3个小球，1个盒子放1个小球，先把小球分组，有C9种，再放到2个盒子中有A1种放法，共有CLM种放法；第二美，2个金子中各放2个小球有CK4种放法.故恰有2个金子不放球的方法有C1U+C3G=84(种).几何中的组合问题［典例1平面内有12个点，其中有4个点共线，此外再无任何3点共线.以这些点为顶点，可构成多少个不同的三角形？［解］法一：以从共线的，个点中取点的多少作为分类的标准.第一英：共线的4个点中有2个点为三角形的项点，共有CSC4=48个不同的三角形；第二美：共线的4个点中有1个点为三角形的顶点，共有C」C&=112个不同的三角形；第三类：关线的4个点中没有，&为三角形的顶点，去有=56个不同的三角形.由分类加法计数原理知，不同的三角形共有48+112+56=216个.法二：(间接法)：从12个点中任意取3个点，有Cf2=220种取法,而在共蝶的4个点中任意取3个均不能构成三角形，即不能构成三角形的情况t C4=4种.故这12个点构成三角形的个数为Ch-Ci=216个.「一—一一—一一—一一慈曾冗丽合向丽而一—一一—一一―:(1)几何组合问题，主要考查组合的知识和空间想象能力，题目多以立体几何中的点、;线、面的位置关系为背景的排列、组合.这类问题情境新颖，多个知识点交汇在一起，综!合牲强.:(2)解答几何组合问题的思考方法与一般的组合问题基本一样,只要把图形的限制条件!视为组合问题的限制条件即可.!(3)计算时可用直接法，也可用间接法，要注意在限制条件较多的情况下，需要分类计.;算符合题意的组合数.…一了薛话而■i■i■■i■i■■i■i■■i■i■i—i■i—i■i—i■正六边形的顶点和中心共7个点，可组成个三角形.解析：不共线的三个点可组成一个三角形，7个点中共线的是过中心的3条对角线，即共有3种情况，故坦成三南形的个数为弓一3=32.答案：32［典例I用。

第2章结构的几何构造分析2.1 复习笔记本章主要用以分析杆件结构的几何构造（或称几何组成），目的在于检查结构是否稳固，能否承受荷载。

本章首先介绍了几何构造分析的几个概念，包括几何不变体系和几何可变体系（几何瞬变体系、几何常变体系）、自由度、约束、多余约束、瞬铰；然后着重介绍了几何不变体系的5种组成规律以及装配思路；最后讲述了平面杆件体系的计算自由度，来帮助更好地分析杆件体系的几何构造。

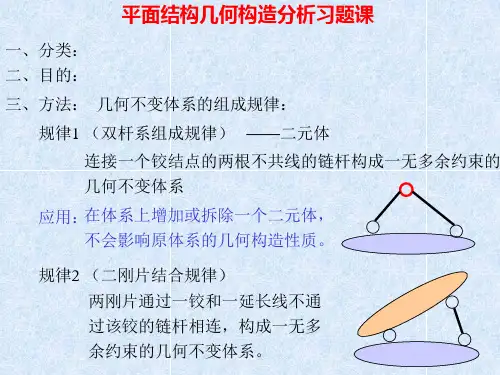
一、几何构造分析的几个概念（见表2-1-1）表2-1-1 几何构造分析的几个概念二、平面几何不变体系的组成规律1．铰结三角形规律平面几何不变体系有5种组成规律，归结为3种装配格式，根据这些基本组成规律或基本装配格式，可以通过2种装配过程，组成各式各样的无多余约束的几何不变体系，具体内容见表2-1-2：表2-1-2 铰结三角形规律注：条件“三铰不共线”和“三链杆不共点”是完全等效的；“三链杆不共点”还包括三链杆延长线组成的瞬铰情况。

2．装配思路（1）从基础出发。

视基础为基本刚片，将周围部件由近及远按照基本装配格式逐级装配，直至形成整体体系。

（2）从内部刚片出发。

在体系内部选取基本刚片，将周围部件按照基本装配格式逐级装配，最后将扩大刚片与地基装配，形成整体体系。

三、平面杆件体系的计算自由度（见表2-1-3）表2-1-3 平面杆件体系的计算自由度W注：①表中m为体系中刚片的个数，j为联系结点个数，g为单刚结点个数，h为单铰结点个数，b为单链杆根数；②n个刚片复结合等于（n－1）个单结合，连接n个结点的复链杆相当于（2n－3）个单链杆。

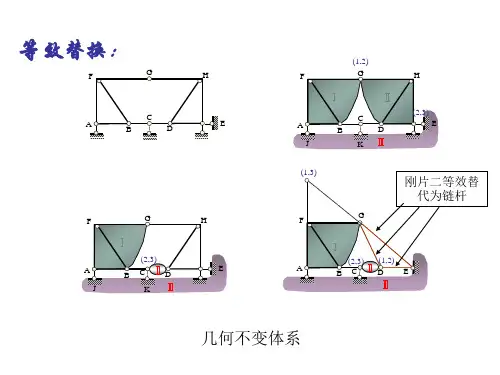
2.2 课后习题详解2-1 试分析图2-2-1所示体系的几何构造。

图2-2-1解：（1）如图2-2-2所示，ABC和DEF为两个二元体，可以撤除，剩下的杆CD通过不共点的三链杆与基础相连，形成几何不变体，二元体不影响原结构的几何不变性，故体系为几何不变体系，且无多余约束。

图2-2-2（2）如图2-2-3所示，刚片AB通过不共点三链杆1、2、3与基础相连，形成几何不变体。

题型一两个计数原理的应用基本原理提供了“完成某件事情”是“分类”进行，还是“分步”进行．在分类或分步中，针对具体问题考虑是与“顺序”有关，还是无关，来确定排列与组合．例1在∠AOB的OA边上取m个点，在OB边上取n个点(均除O点外)，连同O点共m ＋n＋1个点，现任取其中三个点为顶点作三角形，可作的三角形有()A．C1m＋1C2n＋C1n＋1C2mB．C1m C2n＋C1n C2mC．C1m C2n＋C1n C2m＋C1m C1nD．C1m C2n＋1＋C2m＋1C1n[答案] C[解析]第一类：从OA边上(不包括O)任取一点与从OB边上(不包括O)任取两点，可构造一个三角形，有C1m C2n个；第二类：从OA边上(不包括O)任取两点与OB边上(不包括O)任取一点，可构造一个三角形，有C2m C1n个；第三类：从OA边上(不包括O)任取一点与OB边上(不包括O)任取一点，与O点可构造一个三角形，有C1m C1n个．由分类加法计数原理共有N＝(C1m C2n＋C2m C1n＋C1m C1n)个三角形．跟踪训练1现有4种不同颜色要对如图所示的四个部分进行着色，要求有公共边界的两部分不能用同一种颜色，则不同的着色方法共有()A．144种B．72种C．64种D．84种[答案] D[解析]根据所用颜色的种数分类第一类：用4种颜色涂，有A 44＝4×3×2×1＝24(种)．第二类：用3种颜色，必须有一条对角区域涂同色：有C 12C 14A 23＝48(种)．第三类：用2种颜色，对角区域各涂一色有A 24＝4×3＝12(种)．共有24＋48＋12＝84(种)．题型二 排列与组合应用题在解决一个实际问题的过程中，常常遇到排列、组合的综合性问题，而解决问题的第一步是审题，只有认真审题，才能把握问题的实质，分清是排列问题、组合问题，还是综合问题，分清分类与分步的标准和方式，并且要遵循两个原则：一是按元素的性质进行分类；二是按事情发生的过程进行分步．解决排列、组合应用题的常用方法：(1)合理分类，准确分步；(2)特殊优先，一般在后；(3)先取后排，间接排除；(4)集团捆绑，间隔插空；(5)抽象问题，构造模型；(6)均分除序，定序除序．例2 用数字1,2,3,4,5组成没有重复数字的五位数，则其中数字2,3相邻的偶数有________个．(用数字作答)[答案] 18[解析] 数字2和3相邻的偶数有两种情况．第一种情况，当数字2在个位上时，则3必定在十位上，此时这样的五位数共有6个；第二种情况，当数字4在个位上时，且2,3必须相邻，此时满足要求的五位数有A 22A 33＝12(个)，则一共有6＋12＝18(个)．跟踪训练2 停车场一排有12个空位，如今要停放7辆不同的车，要求恰好有4个空位连在一起，求共有多少种停法？解 将4个连在一起的空位看成一个整体，由于另一个空位不能与这个整体相连，则可把这两个元素插在7辆车之间，共有A 28种方法；而7辆车共有A 77种排法，因此共有A 28·A 77＝282240(种)不同停法．题型三 二项式定理的应用对于二项式定理的考查常有两类问题：第一类，直接运用通项公式求特定项或解决与系数有关的问题；第二类，需运用转化思想化归为二项式定理来处理的问题．例3 (1)已知⎝⎛⎭⎫x 2－i x n 的展开式中第三项与第五项的系数之比为－314，其中i 2＝－1，则展开式中系数为实数且最大的项为( )A ．第三项B ．第四项C．第五项D．第五项或第六项[答案] C[解析]T3＝－C2n x2n－5，T5＝C4n x2n－10.由－C2n∶C4n＝－314，得n2－5n－50＝0，∴n＝10，又T k＋1＝C k10(－i)k x520-2k，据此可知当k＝0,2,4,6,8,10时其系数为实数，且当k＝4时，C410＝210最大．(2)已知x2＋x10＝a0＋a1(x＋1)＋…＋a9(x＋1)9＋a10(x＋1)10，则a9的值为________．[答案]－10[解析]方法一所给等式即[1－(x＋1)]2＋[1－(x＋1)]10＝a0＋a1(x＋1)＋…＋a9(x＋1)9＋a10(x＋1)10，而“(x＋1)9”只能从[1－(x＋1)]10中产生，根据二项式定理，得a9＝－C910＝－C110＝－10.方法二因为a9与x9项的系数有关，等式左边x9项的系数为0，所以等式右边x9项的系数也为0.因为x10的系数为a10＝C010＝1，x9的系数为a9·C09＋a10·C110＝a9＋10＝0，所以a9＝－10.小结二项式的展开式的右端整理为f(x)＝a0＋a1x＋a2x2＋…＋a n x n的形式，求多项式的系数和有关的问题用赋值法可以直接得解；若右端整理为f(x)＝a0＋a1(x＋m)＋a2(x＋m)2＋…＋a n(x＋m)n的形式，此时需要先用左端构造出含(x＋m)的二项式，再分析右端系数的规律求解；求具体某项的符号，需要先由左端构造出含(x＋m)的二项式，再把(x＋m)看做一个整体研究其通项，也可以变换右端相关项的因式求解．跟踪训练3(1)(x－1)9按x降幂排列的展开式中，系数最大的项是()A．第4项和第5项B．第5项C．第5项和第6项D．第6项[答案] B[解析]根据二项式系数的性质，(x－1)9的展开式中的中间两项即第5项和第6项的二项式系数最大，但第6项的系数是负数，所以只有第5项的系数最大．(2)已知(x＋2)9＝a0＋a1(x＋1)＋a2(x＋1)2＋…＋a9(x＋1)9，|a1|＋|a2|＋…＋|a9|的值为________．[答案]511[解析]方法一因为(x＋2)9＝[1＋(x＋1)]9＝C09＋C19(x＋1)＋C29(x＋1)2＋…＋C99(x＋1)9，所以a0＝C09＝1，a1＝C19，a2＝C29，…，a9＝C99.因此|a1|＋|a2|＋…＋|a9|＝a1＋a2＋…＋a9＝C19＋C29＋C39＋…＋C99＝29－1＝511.方法二由(x＋2)9＝[1＋(x＋1)]9＝C09＋C19(x＋1)＋C29(x＋1)2＋…＋C99(x＋1)9知，a1，a2，a3，…，a9均为正，所以|a1|＋|a2|＋…＋|a9|＝a1＋a2＋…＋a9.因此，在已知等式中令x＝0，得a0＋a1＋a2＋…＋a9＝29.又a0＝1，所以|a1|＋|a2|＋…＋|a9|＝29－1＝511.[呈重点、现规律]1．两个计数原理分步乘法计数原理与分类加法计数原理是排列、组合中解决问题的重要手段，也是基础方法，尤其是分类加法计数原理与分类讨论有很多相通之处，当遇到比较复杂的问题时，用分类的方法可以有效的将之分解，达到求解的目的．正确地分类与分步是用好两个原理的关键，即完成一件事到底是“分步”进行还是“分类”进行，这是选用计数原理的关键．注意有些复杂的问题往往在分步中有分类，分类中有分步，两个原理往往交错使用．2．排列与组合主要是排列数与组合数计算公式、性质的应用以及排列组合应用题．排列数与组合数计算公式主要应用于求值和证明恒等式，其中求值问题应用连乘的形式，证明恒等式应用阶乘的形式，在证明恒等式时，要注意观察恒等式左右两边的形式，基本遵循由繁到简的原则，有时也会从两边向中间靠拢．对于应用题，则首先要分清是否有序，是排列问题还是组合问题．有限制条件的排列问题，通常从以下两种途径考虑：(1)元素分析法：先考虑特殊元素的要求，再考虑其他元素．(2)位置分析法：先考虑特殊位置的要求，再考虑其他位置．组合应用题的难点是与几何图形有关的问题，此时一般要与两个原理结合应用，还要结合图形的实际意义．排列与组合综合应用题中也有很多重点和难点，比如分配问题，一般方法是先分组，后分配，分组问题又要注意均匀分组和不均匀分组的区别，均匀分组在各组逐一满足后还要除以均匀分组组数的全排列；而有公共元素的分配问题，则可以利用图示法求组数，这样可以避免分组中的重复．3．二项式定理这部分常考知识、题型、主要方法以及注意点大体如下：(1)与二项式定理有关，包括定理的正向应用、逆向应用，题型如证明整除性、近似计算、证明一些简单的组合恒等式等，此时主要是要构造二项式，合理应用展开式；(2)与通项公式有关，主要是求特定项，比如常数项、有理项、x的某次幂等，此时要特别注意二项式展开式中第k＋1项的通项公式是T k＋1＝C k n a n－k b k(k＝0,1，…n)，其中二项式系数是，这是一个极易错点．C k n，而不是C k＋1n(3)与二项式系数有关，包括求展开式中二项式系数最大的项、各项的二项式系数或系数的和、奇数项或者偶数项的二项式系数或系数的和以及各项系数的绝对值的和，主要方法是赋值法，通过观察展开式右边的结构特点和所求式子的关系，确定给字母所赋的值，有时赋值后得到的式子比所求式子多一项或少一项，此时要专门求出这一项，而在求奇数项或者偶数项的二项式系数或系数的和时，往往要两次赋值，再由方程组求出结果，在求各项系数的绝对值的和时，则要先根据绝对值里面数的符号赋值求解．。