第4讲_2-3几何组成分析_习题课

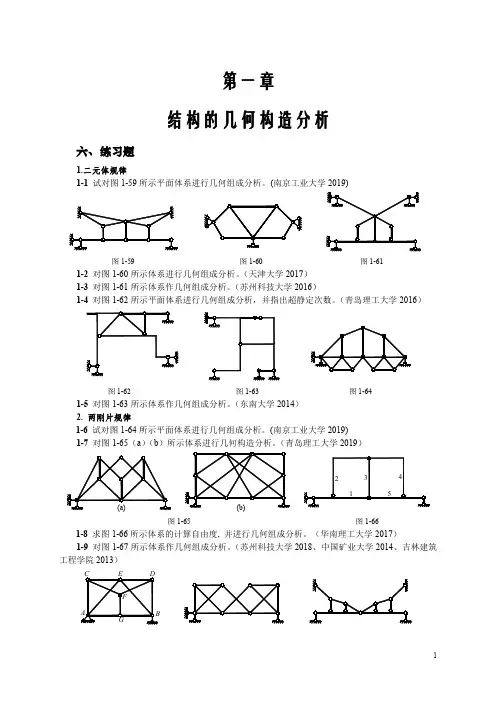
第一章结构的几何构造分析六、练习题1.二元体规律1-1试对图1-59所示平面体系进行几何组成分析。

(南京工业大学2019)(b)a)(c)图1-59图1-60图1-611-2对图1-60所示体系进行几何组成分析。

（天津大学2017）1-3对图1-61所示体系作几何组成分析。

（苏州科技大学2016）1-4对图1-62所示平面体系进行几何组成分析，并指出超静定次数。

（青岛理工大学2016）图1-62图1-63图1-641-5对图1-63所示体系作几何组成分析。

（东南大学2014）2.两刚片规律1-6试对图1-64所示平面体系进行几何组成分析。

(南京工业大学2019)1-7对图1-65（a ）（b ）所示体系进行几何构造分析。

（青岛理工大学2019）图1-65图1-661-8求图1-66所示体系的计算自由度,并进行几何组成分析。

（华南理工大学2017）1-9对图1-67所示体系作几何组成分析。

（苏州科技大学2018、中国矿业大学2014、吉林建筑工程学院2013）图1-67图1-68图1-69 1-10图1-68所示体系的机动分析结论是。

（重庆交通大学2015）3.三刚片规律3.1三个铰都对应于有限点1-11对图1-69所示平面体系进行几何组成分析。

(南京工业大学2019)1-12对图1-70所示体系进行几何组成分析(各点均为铰结点)。

(长沙理工大学2017)图1-70图1-71 1-13图1-71所示体系的计算自由度W=，有个多余约束，为体系。

（哈尔滨工业大学2017）1-14试对图1-72所示平面体系进行几何组成分析。

（哈尔滨工业大学2015）图1-72图1-73图1-74 1-15计算图1-73所示杆件体系的计算自由度，并判断体系符合哪种几何组成规律？（北京工业大学2014）3.2一个无穷远瞬铰1-16对图1-74所示体系进行几何构成分析。

（西安交通大学2015）1-17图1-75所示为（）。

（山东科技大学2018）A.无多余约束的几何不变体系；B.有多余约束的几何不变体系；C.瞬变体系；D.常变体系。

分。

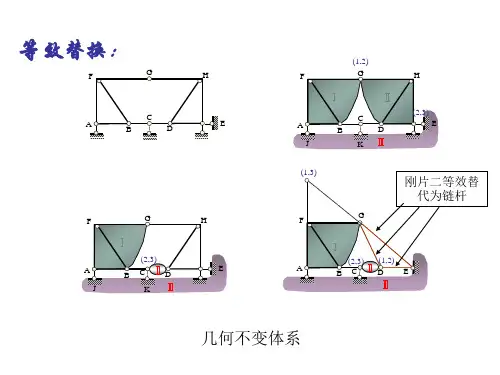
图1 图2 图3解：对图1所示体系进行几何组成分析时，可把地基作为一个刚片，当中的T 字形部分BCE 作为一个刚片。

左边的AB 部分虽为折线，但本身是一个刚片而且只用两个铰与其他部分相联，因此它实际上与A 、B 两铰连线上的一根链杆（如图中虚线所示）的作用相同。

同理，右边的CD 部分也相当于一根链杆。

这样，此体系便是两个刚片用AB 、CD 和EF 三根链杆相联而组成，三杆不全平行也不同交于一点，故为几何不变体系，而且没有多余约束。

对图2所示体系有：去二元体DEBF ；去二元体FBC ；去二元体CB ；AB 杆件与地基刚接构成刚片；整个体系为无多余约束的几何不变体系。

AB 为基本部分，其它为附属部分。

对图3所示体系有：DE 杆件与地基构成几何不变体系；CB 刚片与地基之间用AB 链杆和C 处两个平行链杆相连接，三个链杆不平行也不交与一点满足二刚片规则，故CB 与地基构成几何不变体系；BD 链杆为多余联系；故整个体系为有一个多余约束的几何不变体系。

2、结构位移求解：本题共2题，任选1题作答，计20分。

（1）试求如图4所示外伸梁C 点的竖向位移Cy ∆。

梁的EI 为常数。

（2）已知图5所示结构，422.110 kN m ,10 kN/m EI q =⨯⋅=求B 点的水平位移。

图4 图51、解作P M 和M 图，分别如图(b)、(c)。

BC 段P M 图是标准二次抛物线图形；AB 段P M 图不是标准二次抛物线图形，现将其分解为一个三角形和一个标准二次抛物线图形。

由图乘法可得2224113213828384283()128Cyql l l ql l ql l l l EI ql EI⎡⎤⎛⎫⎛⎫⎛⎫∆=⨯-⨯⨯+⨯⨯⎢⎥⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎣⎦=↓ 2、解：单位和荷载弯矩图，用图乘可求得：29700.14 m B EI∆==3、超静定结构求解：本题共2题，任选1题作答，计20分。

（1）用力法作图6所示结构的M 图.EI =常数。

几何组成分析解题要点
⏹一、机动分析时应灵活运用规则
⏹通常的顺序是：
⏹ 1.二元体规则；
⏹ 2.两钢片规则；
⏹ 3.三钢片规则；
⏹ 4.联合使用多个规则。

⏹二、机动分析的解题要点：
⏹ 1.去掉二元体（若存在）
⏹ 2.当体系用三根链杆按“两钢片规则”与地基相
⏹联时，可去掉支座链杆和地基，只对体系
⏹本身进行分析。

⏹若体系本身几何不变，那么，整个体
⏹系即为几何不变；反之，则为几何可变。

⏹当体系支座链杆多于三根时，则必须把基础视为一钢片，与体系本身一起分析。

⏹ 3.等效代换
⏹⑴等效钢片：
⏹一个几何不变的部分可视为一个钢片。

⏹⑵等效链杆：
⏹复杂形状的链杆（如曲链杆、折线型链
⏹杆）可看作通过铰心的直链杆。

⏹⑶等效虚铰：
⏹联结两钢片的两链杆可用交点的虚铰代
⏹替。

⏹ 4.逐步扩大分析法
⏹⑴从基础出发逐步扩大；
⏹⑵从内部出发逐步扩大。

⏹ 5.两两相联（三钢片规则中）
⏹运用三钢片规则分析时，往往体系比较复杂，应注意以下几点：
⏹⑴选用三个合适的钢片；
⏹⑵找出三个单铰；
⏹⑶注意“两两相联”。

⏹ 6.若体系较复杂，而通过W的计算已知W＞0，
⏹则为可变体系，无需再进行分析。

高中数学1．１空间几何体1.1.１构成空间几何体的基本元素课后训练新人教B版必修２编辑整理：尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望（高中数学 1.１空间几何体1.1．1 构成空间几何体的基本元素课后训练新人教Ｂ版必修２)的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学 1.1 空间几何体 1．1.１构成空间几何体的基本元素课后训练新人教Ｂ版必修2的全部内容。

1。

1．1 构成空间几何体的基本元素课后训练１.下列叙述中,一定是平面的是( ）．A．一条直线平行移动形成的面Ｂ．三角形经过延展得到的面C.组成圆锥的面D.正方形围绕一条边旋转形成的面2.下面空间图形的画法中错误的是( )．３．下列说法正确的是( ).Ａ.四边形是平面图形B.有三个公共点的两个平面必重合C.两两相交的三条直线必在同一个平面内Ｄ.三角形是平面图形４．如图，在正方体ABCD－Ａ１B1C1Ｄ1中，M,N,P，Q分别是线段Ｃ1D1，A1D１,BD1,BC的中点,给出下面四个命题:①ＭＮ∥平面APＣ；②B1Q∥平面AＤD1A１;③A,Ｐ，M三点共线；④平面MNQ∥平面ＡBCD.其中正确的序号为( ).A.①②B.①④C.②③D.③④５．纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北．现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到下侧的平面图形,则标“△”的面的方位是( ）．Ａ.南Ｂ.北Ｃ．西Ｄ.下６.在长方体ＡBCD-Ａ1B1C１D1中（如图所示)，和棱Ａ1B1不相交的棱有__＿_＿＿＿___条．7．若空间三个平面两两相交，则它们的交线条数是__＿_____＿_．８.如图,是一个无盖正方体盒子的表面展开图，A,B,Ｃ为其上三点,则在正方体盒子中,∠AＢC等于____＿__＿__．９.如下图所示,画出(1),（2)中直线ｌ′围绕直线ｌ旋转一周形成的空间几何体．10.如图是边长为1 m的正方体,有一蜘蛛潜伏在A处,B处有一小虫被蜘蛛网粘住,请制作出实物模型，将正方体剪开，描述蜘蛛爬行的最短路线.ﻬ参考答案１.答案:B 直线平行移动可以形成平面或曲面，只有在方向不变的情况下才能得到平面．2。

第四讲 不 定 积 分Ⅰ.考试要求1. 理解原函数的概念，理解不定积分的概念.2. 掌握不定积分的基本公式,掌握不定积分的性质,掌握换元积分法与分部积分法.3. 会求有理函数、三角函数有理式和简单无理函数的积分.Ⅱ. 考试内容一. 原函数的概念1. 定义：原函数定义 如果)()(x f x F =', 或者dx x f x dF )()(=, 则称)(x F 是)(x f 的原函数. 2. 存在性：连续函数有原函数.推论 初等函数在有定义的区间上有原函数. 注：（1）原函数有无穷多.（2）任意两个原函数差一个常数.二. 不定积分的的概念与性质1. 定义：函数)(x f 的全部原函数{+∞<<-∞+C C x F |)(}称为)(x f 的不定积分, 记作⎰dx x f )(.注：（1）不定积分不是一个函数, 而是一个函数的集合.（2）11s i n s i n d x d x C x x-=⎰⎰ 2. 性质基本性质：[])()(x f dx x f dxd=⎰, 或者[]dx x f dx x f d )()(=⎰ ⎰+='C x F dx x F )()(, 或者⎰+=Cx F x dF )()( 运算性质：[()()]f x g xd x αβ+⎰=()()f x d x g x d xαβ+⎰⎰注：当积分号消失时加任意常数三.基本公式1.k d x k x C =+⎰,2.(1)1x x dx C μμμμ=+≠-+⎰, 3. 1ln||d x x C x=+⎰,4.ln x xa a dx C a=+⎰, x xed x e C =+⎰, 5.s i n c o s x d x x C=-+⎰, 6.c o s d s i n xx x C =+⎰, 7.2s e c d t a n x x x C=+⎰, 8.2c s cd c o t x x x C=-+⎰, 9.s e ct a n d s e c x x x xC =+⎰， 10.c s c c o td c s c x x x xC =-+⎰，11. 221a r c s i n xd x Ca a x=+-⎰, 12.2211a r c t a n xd x C a x a a=++⎰, 13.s e c d l n |s e c t a n |x x x xC =++⎰， 14. c s c d l n |c s c c o t|x x x xC =-++⎰，15.2211l n ||2a xd x C a x a a x+=+--⎰. 16. 22221l n ()d x x x a Cx a=+±+±⎰. 注：不能用初等函数表示的积分2x e d x ⎰,2x ed x -⎰,s in x d x x ⎰,1ln d x x⎰. 四. 基本积分方法1. 换元积分法：()()[()]()x t f x d x f t td t ϕϕϕ='⎰⎰ 2.常见换元公式 （1）1()()()fa xb d x fa xb d a xb a +=++⎰⎰,（2）11()()f x x d x f x d x μμμμμ-=⎰⎰, （3）1()()l n x x x xf aa d x f ad a a=⎰⎰,（4）(s i n )c o s (s i n )s i n f x x d x f x dx =⎰⎰, （5）(c o s )s i n (c o s )c o s f x x d x f x dx =-⎰⎰, （6）21(s i n )(s i n )s i n 1f a r c x d x f a r c x d a r c x x=-⎰⎰, （7）21(a r c t a n )(a r c t a n )a r c t a n 1f x d x f x d x x=+⎰⎰, （8）22(,)Rxa x d x -⎰， 令22a x -，令t a x sin =,22ππ≤≤-t ；（9）22(,)Rxa x d x +⎰， 令t a x tan =, 22ππ<<-t .（10）22(,)Rx x a d x -⎰，令t a x sec =, 20π<<t 或02<<-t π, （11）(,)nax bR x dx cx d++⎰，令na x bu cx d+=+，其中，0a d b c -≠，2,3,4,n =（12）(s i n ,c o s )R x xd x ⎰，令ta n 2x u = 分母次数较高时，倒代换1x t=；a xe t =，a r c s i n x t = 3.分部积分法:⎰⎰'-='vdxu uv dx v u . 注：反对幂三指（1）()s i n n P x a x d x ⎰，()c o s n P x a x d x ⎰，()a xn P x e dx ⎰ （2）()a r c s i n nPx a x d x ⎰，()a r c c o s nPx a x d x ⎰，()l n nP x x d x ⎰ （3）s i n ()k xe a x bd x+⎰Ⅲ．题型与例题【例1】d xx x ++-⎰11.【例2】计算下列不定积分 【例3】计算不定积分dx x x x⎰-)1(arccos 2.【例4】求计算不定积分.)1(232arctan dx x xe x ⎰+【例5】⎰+dx exe xx 1【例6】计算不定积分⎰+dx xx xcos sin sin 【例7】求dx xxx x ⎰-2sin cos sin .【例8】（11317）（本题满分10分）求arcsin ln x xdx x+⎰. 【例9】设x xx f sin )(sin 2=，求⎰-dx x f xx )(1 【例10】设函数f x ()有连续导函数, 且f x d x x x C ()(s i n )l n =++⎰1, 求 xf x d x '⎰().第五讲 定积分及其应用Ⅰ.考试要求1. 理解定积分的概念．2. 掌握定积分的性质及定积分中值定理，掌握换元积分法与分部积分法．3. 会求有理函数、三角函数有理式和简单无理函数的积分．4. 理解积分上限的函数，会求它的导数，掌握牛顿－莱布尼茨公式．5. 了解反常积分的概念，会计算反常积分． 注：（1）数一、数二要求：掌握用定积分表达和计算一些几何量与物理量（平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等）及函数的平均值．（2）数三要求：会利用定积分计算平面图形的面积、旋转体的体积和函数的平均值，会利用定积分求解简单的经济应用问题．Ⅱ.考试内容一、定积分的概念与性质1. 定义∑⎰=→∆∆ni i i ba x f dx x f 1)(lim )(ξλ； 注：（1）积分与所用变量的符号无关. （2）规定：()()baab f xd x f xdx =-⎰⎰, ()0a af x dx =⎰.（3）几何意义（4）设)(x f 在[,]a b 上可积，则1011l i m ()()nn k ba ba fa k fx d x n n n →∞=--+=∑⎰ 特别地， ⎰∑==∞→101)()(1lim dx x f n kf n n k n ． 【例1】求和式极限（1）222121l i m []n n n n n→∞-+++ （2）222222l i m []12n n n nn n n n→∞++++++（3）12l i m [1c o s 1c o s 1c o s ]n n nnn nπππ→∞++++++（4）!l i mnn n n→∞2. 可积的条件（1）可积的必要条件：若)(x f 在],[b a 上可积，则)(x f 在],[b a 上有界． （2）可积的充分条件：若)(x f 在],[b a 上连续或仅有有限个间断点，则)(x f 在],[b a 上可积； 3. 定积分的性质假设各性质中所列出的定积分都是存在的． （1）⎰⎰⎰±=±bababa dx x g dx x f dx x g x f )()()]()([βαβα． （2）⎰⎰⎰+=bcc a ba dx x f dx x f dx x f )()()(． 注：分段函数的积分（3）若在],[b a 上()()f x g x ≤，则()()bbaaf xd xg xd x ≤⎰⎰．|()||()|()bbaaf x d x f x d x b a ≤>⎰⎰． （4）设M 与m 分别是)(x f 在],[b a 上最大值与最小值，则 )()()(a b M dx x f a b m ba -≤≤-⎰． （5）积分中值定理：若)(x f 在],[b a 上连续，则存在],[b a ∈ξ，使得)()()(ξf a b dx x f ba-=⎰. 注：① ξ可以在区间内部取到.② 若)(x f 在],[b a 上连续，()g x 在],[b a 上可积且定号,则],[b a ∈ξ，使得()()()()b baaf xg x d x f g x d x ξ=⎰⎰. 【例2】 （11304）设⎰=4sin ln πxdx I ,⎰=4cot ln πxdx J ,⎰=40cos ln πxdxK ,则I ,J ,K 的大小关系是[ ]．)(A K J I <<. )(B J K I <<. )(C K I J <<. )(D I J K <<. 【例3】 设函数)(x f y =在区间]1,0[上可导, 且⎰=2/10)(2)1(dx x xf f , 则存在(0,1)ξ∈, 使得0)()(=+'ξξξf f二、奇偶函数与周期函数的积分性质1. 若)(x f 在],[a a -上可积，则⎪⎩⎪⎨⎧=⎰⎰-为偶函数若为奇函数若)(,)(2)(,0)(0x f dx x f x f dx x f a aa ． 2. 若)(x f 在],[a a -上可积，则⎩⎨⎧⎰为偶函数若奇函数为奇函数若偶函数为)(,)(,)(0x f x f dt t f x． 注：若)(x f 为奇函数，则)(x f 的原函数均为偶函数．若)(x f 为偶函数，则原函数中只有一个原函数是奇函数． 3. 设)(x f 是以T 为周期的可积函数，则任意周期上的积分相等.⎰⎰⎰-+==2/2/0)()()(T T T Ta a dxx f dx x f dx x f ， ⎰⎰=T nTdx xf n dx x f 00)()(． 4. 设)(x f 是以T 为周期的连续函数，则)(x f 的原函数以T 为周期的充分必要条件是0)(0=⎰Tdx x f ．【例4】积分=+⎰-22223cos )sin (ππxdt x x ________． 【例5】设)(x F 是连续函数)(x f 的一个原函数，“N M ⇔”表示M 的充要条件是N ，则必有 [ ]．（A ）)(x F 是偶函数 ⇔)(x f 是奇函数．（B ）)(x F 是奇函数 ⇔)(x f 是偶函数． （C ）)(x F 是周期函数 ⇔)(x f 是周期函数． （D ）)(x F 是单调函数 ⇔)(x f 是单调函数． 【例6】设函数⎰=xdt t x S 0cos)(， （1）当n 为正整数，且ππ)1(+≤≤n x n 时，证明：)1(2)(2+<≤n x S n ； （2）求xx S x )(lim+∞→.三、计算定积分1. 微积分基本公式（牛顿－莱布尼茨公式）：若)(x f 在],[b a 上连续，)(x F 是)(x f 在],[b a 上的一个原函数，则)()()(a F b F dx x f ba-=⎰． 2. 换元积分法与分部积分法 注：换元要换限 【例7】计算⎰--2ln 021dx e x 。

第4章 二次曲线和二次曲面习题4.11.在直角坐标系x O y 中，以直线:43120l x y -+=为新坐标系的x '轴，取通过(1,3)A -且垂直于l 的直线为y '轴，写出点的坐标变换公式， 并且求直线1:3250l x y -+=在新坐标系中的方程。

解：直线:43120l x y -+=的方向是(3,4)，与它垂直的方向是(4,3)±-，新坐标系的x '轴的坐标向量取为34(,)55，y '轴坐标向量取为43(,)55-，与直线:43120l x y -+=垂直且的直线方程可设为340x y c ++=，由于过点(1,3)A -，得到直线方程是3490x y ++=，两直线的交点(3,0)-是新坐标原点，所以点的坐标变换公式：34355.43055x x y y ⎡⎤-⎢⎥'-⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦直线1:3250l x y -+=在新坐标系中的方程：13443:3(3)2()505555l x y x y ''''---++=，化简有1:18200.l x y ''--=2.作直角坐标变换，已知点(6,5),(1,4)A B --的新坐标分别为(1,3),(0,2)-，求点的坐标变换公式。

解：设同定向的点的坐标变换公式是：cos sin .sin cos x x a y y b θθθθ'-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦它的向量的坐标变换公式是：cos sin .sin cos u u v v θθθθ'-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦由题意知向量(5,1) A B =-变为(1,5)A B ''=-，于是有5cos sin 1.1sin cos 5θθθθ---⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦得到125s i n ,c o s .1313θθ==于是点的坐标变换公式是：5121313.1251313x x a y y b ⎡⎤-⎢⎥'⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦将点(1,4)B -及它的像点(0,2)代入得到3713,6213a b ⎡⎤⎢⎥⎡⎤=⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦所以点的坐标变换公式是： 51237131313.12562131313x x y y ⎡⎤⎡⎤-⎢⎥⎢⎥'⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦设反定向的点的坐标变换公式是：cos sin .sin cos x x a y y b θθθθ'-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦它的向量的坐标变换公式是：cos sin .sin cos u u v v θθθθ'-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦由题意知向量(5,1)A B =-变为(1,5) A B ''=-，于是有5cos sin 1.1sin cos 5θθθθ---⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦得到s i n 1,c o s 0.θθ=-=于是点的坐标变换公式是：01.10x x a y y b '-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'-⎣⎦⎣⎦⎣⎦⎣⎦将点(1,4B -及它的像点(0,2)代入得到3,4a b ⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦所以点的坐标变换公式是： 013.104x x y y '-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'--⎣⎦⎣⎦⎣⎦⎣⎦3.设新旧坐标系都是右手直角坐标系，点的坐标变换公式为5,3,22(1)(2) 2.3;22x x y x y y x y x y ⎛''=++ '=-+⎧⎨' =-⎩''=-+- ⎝ 其中，(,)x y 与(,)x y ''分别表示同一点的旧坐标与新坐标，求新坐标系的原点的旧坐标，并且求坐标轴旋转的角θ。

题15．7试对图示体系进行几何组成分析。

解 (1)计算自由度。

体系的自由度为W- 2j -6-r=2×8-9-7=0(2)几何组成分析。

首先把三角形ACD和BCE分别看做刚片I和刚片Ⅱ，把基础看做刚片I，则三个刚片用不共线的三个铰A、B、C分别两两相联，组成一个大的刚片。

在这个大的刚片上依次增加二元体12、DGF、CHG、EIH、IJ3。

最后得知整个体系为几何不变，且无多余约束。

题15.8试对图示体系进行几何组成分析。

解 (1)计算自由度。

体系的自由度为W- 3m - 2h -r=3×6-2×7—4=0(2)几何组成分析。

刚片AF和AB由不共线的单铰A以及链杆DH相联，构成刚片I，同理可把BICEG部分看做刚片Ⅱ，把基础以及二元体12、34看作刚片I，则刚片I、Ⅱ、Ⅲ由不共线的三个铰F、B、G两两相联，构成几何不变体系，且无多余约束。

题15.9试对图示体系进行几何组成分析。

解 (1)计算自由度。

体系的自由度为W- 3m - 2h -r=3×14 -2×19 -4一O(2)几何组成分析。

在刚片HD上依次增加二元体DCJ、CBI、BAH构成刚片I，同理可把DMG部分看做刚片Ⅱ，把基础看做刚片I，则刚片I、Ⅱ、Ⅲ由不共线的单铰D，虚铰N、O 相联，构成几何不变体系，且无多余约束。

题15.10试对图示体系进行几何组成分析。

解 (1)计算自由度。

体系的自由度为W-2j—b-r=2×7—11-3一O(2)几何组成分析。

由于AFG部分由基础简支，所以可只分析AFG部分。

可去掉二元体BAC只分析BFGC部分。

把三角形BDF、CEG分别看做附片I和I，刚片I和I由三根平行的链杆相联，因而整个体系为瞬变。

题15.11试对图示体系进行几何组成分析。

解 (1)计算自由度。

体系的自由度为W- 2j -6-r=2×9-13—5一O(2)几何组成分析。

首先在基础上依次增加二元体12、AE3、AFE、ABF、FI4，成一个大的刚片I。