稳恒电流和稳恒磁场1 恒定电流

41 磁 学基本内容一、稳恒磁场 磁感应强度1． 稳恒磁场电流、运动电荷、永久磁体在周围空间激发磁场。

稳恒磁场是指不随时间变化的磁场。

稳恒电流激发的磁场是一种稳恒磁场。

2． 物质磁性的电本质无论是永磁体还是导线中的电流，它们的磁效应的根源都是电荷的运动。

因此，磁场是运动电荷的场。

3． 磁感应强度磁感应强度B是描述磁场的基本物理量，它的作用与E 在描述电场时的作用相当。

磁场对处于其中的载流导线、运动电荷、载流线圈、永久磁体有力及力矩的作用。

可以根据这些作用确定一点处磁场的强弱和方向——磁感应强度B。

带电q 的正点电荷在磁场中以速度v运动，若在某点不受磁力，则该点磁感应强度B 的方向必与电荷通过该点的速度v平行。

当该电荷以垂直于磁感应强度B 通过该点时受磁力⊥F ，则该点磁感应强度大小qvF B ⊥=，且⊥F ，v ，B两两互相垂直并构成右手系。

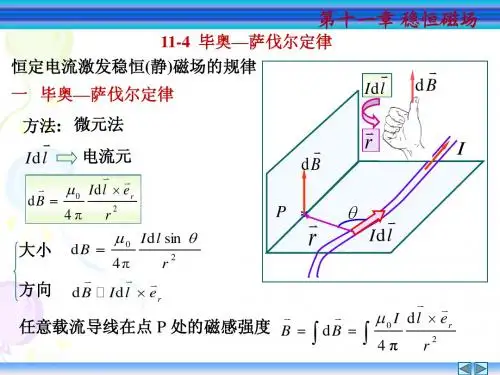
二、毕奥—萨伐尔定律 运动电荷的磁场1． 磁场的叠加原理空间一点的磁感强度等于各电流单独存在时在该点产生磁感应强度的矢量和：∑=ii B B 可推广为 ⎰=B d B42B d是电流强度有限而长度无限小的电流元l d I 或电流强度无限小而空间大小不是无限小的元电流的磁场。

上式中矢量号一般不能略去，只有当各电流产生磁场方向相同时，才能去掉矢量号。

2． 毕奥—萨伐尔定律电流元l d I 在空间一点产生的磁场B d为： 304rr l d I B d πμ⨯= 大小： 02I sin(I ,r)dB 4r dl dl μπ∠=方向：B d 垂直于电流元l d I 与r 所形成的平面，且B d与l d I 、r构成右手螺旋。

3． 电流与运动电荷的关系导体中电荷定向运动形成电流，设导体截面积为S ，单位体积载流子数为n 。

每个载流子带电q ，定向运动速率为v ，则nqvS I =。

电量为q 的带电体作半径为R 、周期为T 的匀速圆周运动相当于半径为R 、电流强度T q I /=的圆电流，具有磁矩TqR I R p m 22ππ==。

大学物理 恒定电流稳恒磁场知识点总结1. 电流强度和电流密度 电流强度：单位时间内通过导体截面的电荷量 （电流强度是标量，可正可负）；电流密度：电流密度是矢量，其方向决定于该点的场强E 的方向（正电荷流动的方向），其大小等于通过该点并垂直于电流的单位截面的电流强度dQ I dt =， dIj e dS= ， S I j dS =⎰⎰ 2. 电流的连续性方程和恒定电流条件 电流的连续性方程：流出闭合曲面的电流等于单位时间闭合曲面内电量增量的负值（其实质是电荷守恒定律）dqj dS dt=-⎰⎰ ， （ j tρ∂∇=-∂ ）； 恒定电流条件： 0j dS =⎰⎰ ， （ 0j ∇= ） 3. 欧姆定律及其微分形式： UI R=， j E σ=， ，焦耳定律及其微分形式： 2Q A I Rt == 2p E σ= 4. 电动势的定义：单位正电荷沿闭合电路运行一周非静电力所作的功AK dl q ε+-==⎰ ， K dl ε=⎰5. 磁感应强度：是描述磁场的物理量，是矢量，其大小为0sin FB q v θ=，式中F 是运动电荷0q 所受洛伦兹力，其方向由 0F q v B =⨯决定 磁感应线：为了形象地表示磁场在空间的分布，引入一族曲线，曲线的切向表示磁场的方向，密度是磁感应强度的大小；磁通量：sB dS φ=⎰⎰ （可形象地看成是穿过曲面磁感应线的条数）6．毕奥一萨伐尔定律： 034Idl r dB r μπ⨯=34L Idl rB r μπ⨯=⎰7．磁场的高斯定理和安培环路定理磁场的高斯定理： 0SB dS =⎰⎰、 （ 0B ∇= ） （表明磁场是无源场）安培环路定理：0i LiB dl I μ=∑⎰、LSB dl j dS =⎰⎰⎰ 、(0B j μ∇⨯=)（安培环路定理表明磁场是有旋场）8．安培定律： dF Idl B =⨯ 、L F Idl B =⨯⎰磁场对载流线圈的作用: M m B =⨯ (m 是载流线圈的磁矩m IS =)9．洛伦兹力：运动电荷所受磁场的作用力称为洛伦兹力f qv B =⨯带电粒子在匀强磁场中的运动：运动电荷在匀强磁场中作螺旋运动，运动半径为mv R qB⊥=、周期为 2m T qB π= 、螺距为 2mv h v T qB π==霍尔效应 ： 12HIBV V K h-= 式中H K 称为霍尔系数，可正可负，为正时表明正电荷导电，为负时表明负电荷导电 1H K nq=10．磁化强度 磁场强度 磁化电流 磁介质中的安培环路定理mM τ∑=∆ 、 LL M dl I =∑⎰，内、n i M e =⨯， 0BH M μ=- 、m M H χ= 、 00m r B H H μχμμμ==（1+）H=、 0i LiH dl I =∑⎰、LSH dl j dS =⎰⎰⎰。

11-1 恒定电流电流密度磁现象：我国是世界上最早发现和应用磁现象的国家之一，早在公元前300年久发现了磁铁矿石吸引铁的现象。

在11世纪，我国已制造出航海用的指南。

在1820年之前，人们对磁现象的研究仅局限于铁磁极间的相吸和排斥，而对磁与电两种现象的研究彼此独立，毫无关联。

1820年7月丹麦物理学家奥斯特发表了《电流对磁针作用的实验》，公布了他观察到的电流对磁针的作用，从此开创了磁电统一的新时代。

奥斯特的发现立即引起了法国数学家和物理学家安培的注意，他在短短的几个星期内对电流的磁效应作出了系列研究，发现不仅电流对磁针有作用，而且两个电流之间彼此也有作用，如图所示；位于磁铁附近的载流线圈也会受到力或力矩的作用而运动。

此外，他还发现若用铜线制成一个线圈，通电时其行为类似于一块磁铁。

这使他得出这样一个结论：天然磁性的产生也是由于磁体内部有电流流动。

每个磁性物质分子内部，都自然地包含一环形电流，称为分子电流，每个分子电流相当于一个极小的磁体，称为分子磁矩。

一般物体未被磁化时，单个分子磁矩取向杂乱无章，因而对外不显磁性；而在磁性物体内部，分子磁矩的取向至少未被完全抵消，因而导致磁铁之间有“磁力”相互作用。

1820年是人们对电磁现象的研究取得重大成果的一年。

人们发现，电荷的运动是一切磁现象的根源。

一方面，运动电荷在其周围空间激发磁场；另一方面，运动电荷在空间除受电场力作用之外，还受磁场力作用。

电磁现象是一个统一的整体，电学和磁学不再是两个分立的学科。

11-1 恒定电流电流密度如前所述，电荷的运动是一切磁现象的根源。

电荷的定向运动形成电流，称为传导电流；若电荷或宏观带电物体在空间作机械运动，形成的电流称为运流电流。

常见的电流是沿着一根导线流动的电流，其强弱用电流强度来描述，它等于单位时间通过某一截面的电量，方向与正电荷流动的方向相同，其数学表达式为dtdq I ，虽然我们规定了电流强度的方向，但电流强度I 是标量而不是矢量，因为电流的叠加服从代数加减法则，而不服从矢量叠加的平行四边形法则。