静电场稳恒电流与电场稳恒磁场电磁场

关于静电场、稳恒电场和感应电场的教学研究《高中物理读本》（即甲种本）第二册的“电场”一章详细阐述了静止电荷所激发的电场——静电场的特性，并在学生实验之五——“电场中等势线的描绘”实验中用脚注说明由于静电场和稳恒电流场遵守的规律相似，实验中是用在导电纸上形成的稳恒电场模拟静电场来做实验；在第三册（甲种本）的“电磁振荡和电磁波”一章中介绍了麦克斯韦电磁场理论之一：变化的磁场能够在周围的空间产生电场，指出这种电场为感应电场或涡旋电场，与静电场、稳恒电场有本质的不同．由于教材对后两类场讲得很少，在高考要求中属A类要求，教师在教学过程中常常一带而过，使得学生对这三类场的区别和联系存在模糊认识．作者在相关章节的综合教学过程中，对这三类场的共性和各自的特点采取了深入浅出的教学手法，通过对比的方法进行教案的组织和课堂教学的实施，教学效果非常良好．本文对这三类场的共同点和各自的特性谈谈一些认识．1 静电场、稳恒电场和感应电场的共性（1）它们都是电场，是物质的一种客观存在形式，都储存着电能；（2）它们对处于其中的电荷都有电场力的作用；（3）在这三种电场中移动电荷时相应的电场力一般都要做功．2 电场与稳恒电场的个性2.1 静电场的个性（1）静电场由静止电荷所激发的电场称为静电场，因此静电场是有源场．对于一个封闭曲面，静电场的电场线穿出曲面的条数与穿进曲面的条数之差正比于该曲面内所包含电荷电量的代数和，这是著名的关于静电场的高斯定理．另外，静电场是保守力场，即在静电场中经过不同的路径将点电荷从一处移到另一处时静电场力对电荷所做的功是完全一样的，这是关于静电场另一定理——环路定理．静电场的这一性质类似于大家非常熟悉的重力场，所以我们也可以在静电场中引入电势差来描述在将单位正电荷从一点移到另一点时电场力对它所做的功．在带电体系的电荷分布在有限空间的情况下，我们可以取无限远处的电势为零，这样静电场中各处的电势就有了确定的值．此外，作为形象描述静电场的电场线的特点是：由正电荷（或无限远）发出，终止于负电荷（或无限远）；电场线在没有电荷的地方不会中断；电场线上各点的电势沿电场线方向不断降低．（2）静电场中的导体在静电场中常常有一些导体存在．导体的特殊性在于它内部存在自由电子．导体内一旦有电场存在，这些电子就会定向运动．在静电平衡状态下，导体内部的场强必为零；而导体表面的场强与导体表面相垂直（否则电子将在导体内或沿导体的表面运动）．此外，在静电平衡状态下导体内部不带电，导体所带电荷只能分布于导体的表面；导体的表面是等势面，整个导体是个等势体．2.2 稳恒电场的个性当电荷在导体内做定向流动而形成稳恒电流时，在导体内外所存在的电场称为稳恒电场或恒定电场．在稳恒电流情况下尽管电荷在流动，但由于导体内及其表面的电荷分布是不随时间变化的，所以从这一点看，稳恒电场在本质上与由静止电荷所激发的静电场是相同的：遵守高斯定理和环路定理；是保守力场，也可以引入电势进行描述；稳恒电场的电场线的性质与描写静电场的电场线的性质亦完全相同．高中第二册（甲种本）的学生实验之五：电场中等势线的描绘就是利用这一等价性，用稳恒电场来模拟静电场．需要指出的是，稳恒电场仍有它的特殊性：（1）由于导体总存在电阻，导体中要建立稳恒电流就必须将导体与电源相连接，形成一闭合的回路．（2）正是由于导体中稳恒电场的存在，电荷才得以在导体中流动．因此，与静电平衡状态下的导体不同，稳恒电流条件下导体内部可以带电，导体内部的场强亦可以不为零．（3）我们知道静电场的电场线在一般情况下并不是电荷运动的轨迹线，但是，导体中稳恒电场的电场线就是电荷流动的轨迹线．在外电路，导体中电荷—电子是逆着导体中稳恒电场的方向，从电源负极处流向电源正极处；在电源的内部，电源消耗能量使得电子顺着电场线方向从正极流到负极。

大学物理电磁学总结一、三大定律库仑定律：在真空中，两个静止的点电荷q1 和q2 之间的静电相互作用力与这两个点电荷所带电荷量的乘积成正比，与它们之间距离的平方成反比，作用力的方向沿着两个点电荷的连线，同号电荷相斥，异号电荷相吸。

uuu r q q ur F21 = k 1 2 2 er rur u r 高斯定理：a) 静电场：Φ e = E d S = ∫s∑qiiε0（真空中）b) 稳恒磁场：Φ m =u u r r Bd S = 0 ∫s环路定理：a) 静电场的环路定理：b) 安培环路定理：二、对比总结电与磁∫Lur r L E dl = 0 ∫ ur r B dl = 0 ∑ I i （真空中）L电磁学静电场稳恒磁场稳恒磁场电场强度：E磁感应强度：B 定义：B =ur ur F 定义：E = (N/C) q0基本计算方法：1、点电荷电场强度：E =ur r u r dF （d F = Idl × B ）(T) Idl sin θ方向：沿该点处静止小磁针的N 极指向。

基本计算方法：urq ur er 4πε 0 r 2 1r ur u Idl × e r 0 r 1、毕奥-萨伐尔定律：d B = 2 4π r2、连续分布的电流元的磁场强度：2、电场强度叠加原理：ur n ur 1 E = ∑ Ei = 4πε 0 i =1r qi uu eri ∑ r2 i =1 inr ur u r u r 0 Idl × er B = ∫dB = ∫ 4π r 23、安培环路定理（后面介绍）4、通过磁通量解得（后面介绍）3、连续分布电荷的电场强度：ur ρ dV ur E=∫ e v 4πε r 2 r 0 ur σ dS ur ur λ dl ur E=∫ er , E = ∫ e s 4πε r 2 l 4πε r 2 r 0 04、高斯定理（后面介绍）5、通过电势解得（后面介绍）几种常见的带电体的电场强度公式：几种常见的磁感应强度公式：1、无限长直载流导线外：B = 2、圆电流圆心处：B = 3、圆电流轴线上：B =ur 1、点电荷：E =q ur er 4πε 0 r 2 10 I2R0 I 2π r2、均匀带电圆环轴线上一点：ur E=r qx i 2 2 32 4πε 0 ( R + x )R 2 IN 2 ( x 2 + R 2 )3 21 0α 23、均匀带电无限大平面：E =σ 2ε 0（N 为线圈匝数）4、无限大均匀载流平面：B =4、均匀带电球壳：E = 0( r < R )（α 是流过单位宽度的电流）ur E=q ur er (r > R ) 4πε 0 r 25、无限长密绕直螺线管内部：B = 0 nI （n 是单位长度上的线圈匝数）6、一段载流圆弧线在圆心处：B = （是弧度角，以弧度为单位）7、圆盘圆心处：B =r ur qr (r < R) 5、均匀带电球体：E = 4πε 0 R 3 ur E= q 4πε 0 r ur er (r > R ) 20 I 4π R0σω R2（σ 是圆盘电荷面密度，ω 圆盘转动的角速度）6、无限长直导线：E =λ 2πε 0 x λ 0(r > R ) 2πε 0 r7、无限长直圆柱体：E =E=λr (r < R) 4πε 0 R 2电场强度通量：N·m2·c-1）（磁通量：wb）（sΦ e = ∫ d Φ e = ∫ E cos θ dS = ∫s sur u r E d S通量u u r r Φ m = ∫ d Φ m = ∫ Bd S = ∫ B cos θ dS s s s若为闭合曲面：Φ e =∫sur u r E d S若为闭合曲面：u u r r Φ m = Bd S = B cos θ dS ∫ ∫s s均匀电场通过闭合曲面的通量为零。

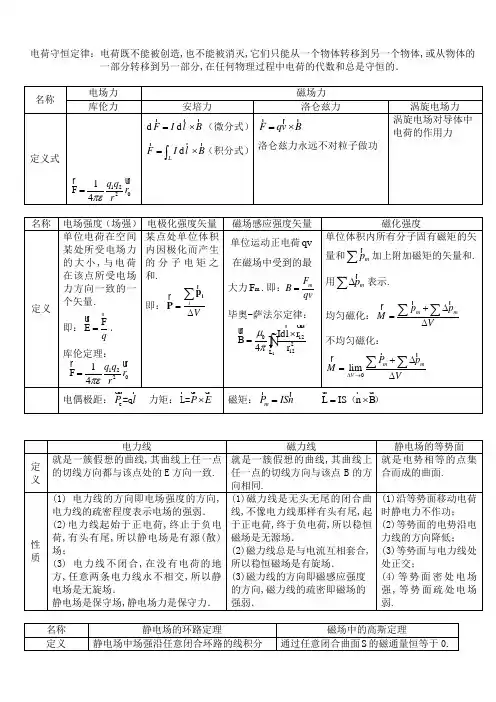
电荷守恒定律：电荷既不能被创造,也不能被消灭,它们只能从一个物体转移到另一个物体,或从物体的一部分转移到另一部分,在任何物理过程中电荷的代数和总是守恒的．人生在搏，不索何获电位差（电压）：单位正电荷的电位能差．即：B AB ABABA W A U Edl q q===⎰u r r ．人生在搏，不索何获人生在搏，不索何获电场和磁场的本质及内在联系：静电场问题求解基础问题1.场的唯一性定理：①已知V 内的自由电荷分布②V 的边界面上的φ值或n ∂∂/φ值，则V 内的电势分布，除了附加的常数外，由泊松方程ερφ/2-=∇及在介质分界面上的边值关系σφφεεφφ-=∂∂-∂∂=)()(,nn jiji唯一的确定。

两种静电问题的唯一性表述：⑴给定空间的电荷分布，导体上的电势值及区域边界上的电势或电势梯度值→空间的电势分布和导体上的面电荷分布（将导体表面作为区域边界的一部分）⑵给定空间的电荷分布，导体上的总电荷及区域边界上的电势或电势梯度值→空间的电势分布和导体上的面电荷分布（泊松方程及介质分界面上的边值关系）2.静电场问题的分类：分布性问题：场源分布E ⇔ρ电场分布边值性问题：场域边界上电位或电位法向导数→电位分布和导体上电荷分布3.求解边值性问题的三种方法： 分离变量法①思想：根据泊松方程初步求解φ的表达式，再根据边值条件确定其系数电像法①思想：根据电荷与边值条件的等效转化，用镜像电荷代替导体面（或介质面）上的感应电荷（或极化电荷） 格林函数法①思想：将任意边值条件转化为特定边值条件，根据单位点电荷来等价原来边界情况 静电场，恒流场，稳恒磁场的边界问题：电荷电场磁场电流变化 变化运动激发激发电磁场的认识规律一．静电场的规律： 1.真空中的静电场； 电场强度EdvR Rz y x z y x E v ρϖ3)',','(41),,(,ρπε⎰=电场电势V 静电场的力F 静电场的能量2.介质中的静电场； 电位移矢量D0ε=+D E P v v v极化强度PE p ρρ)(0εε-= e 0P E χε=u r u r （各向同性介质）二．稳恒磁场与稳恒电流场1.真空中的磁场强度B31212114R R L d I u B c ϖρϖ⨯=⎰πdv R R r J ur B v 30)'(4)(ϖϖϖ⨯=⎰π'430,dV R R v B ⋅⨯=⎰Ωϖϖϖρπμdq R R v v304ϖϖ⨯=⎰πμ304R R v q πμϖϖ⨯=2.真空中的电流密度Jtj ∂∂-=•∇ρ荷密度J ρν=⋅3.磁场矢位A')'(140dv r J R A v ϖϖρ⎰=πμ，A B ρρ⨯∇=4.介质中的磁场感应强度HH B μ=5.磁化强度MH )1(ρϖ-=r u M （各向m M H χ=r r 同性介质）6.磁场中的力F7.磁场中的能量三．麦克斯韦方程组与介质中的麦克斯韦方程组实质：反映场与电荷及其运动形式（电流）的联系，揭示电场与磁场的相互转换关系电荷：（自由电荷，极化电荷）D ρ∇⋅= P ρρ∇⋅=-电流：（传导电流，位移电流，磁化电流）M J M ϖϖ⨯∇=， t E t D J D ∂∂=∂∂=ρρϖε，0=∂∂+⋅∇t J ρϖ麦克斯韦方程组与介质中的麦克斯韦方程组包含是各种矢量的散度与旋度运算，有微分，积分形式两种⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⋅⋅=⋅⋅+=⋅-=⋅⎰⎰⎰⎰⎰⎰0s d B Q s d D s d D dtd I l d H s d B dt d l d E p s s f u s u ϖϖϖϖϖϖϖϖϖρϖϖ（自由电荷） ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⋅∇=⋅∇∂∂+=⨯∇∂∂-=⨯∇0B E t E J B t BE ϖϖϖϖϖϖϖερεμμ四．三大定律：欧姆定律E J ϖρσ=焦耳定律 安倍定律五．守恒定律： 电荷守恒 能量守恒六．在边界条件下的电磁现象：⎪⎪⎪⎩⎪⎪⎪⎨⎧=-⨯=-⨯=-⋅=-⋅=-⋅传导电流面密度）自由电荷面密度），或()(0)(0)()(()(1212201212S S S J H H n E E nB B nE E n D D n ϖϖϖϖϖϖϖϖϖϖϖϖϖϖερρ七．静电场与稳恒磁场的比较：八电磁波在空间的传播1.亥姆霍兹方程2.电磁波在介质分界面的反射与折射菲涅耳公式布儒斯特角全反射垂直入射3.电磁波在导波结构中传播导波的分类矩形波导传输线理论4.电磁波传播的边界条件电磁波的辐射1.达朗贝尔方程库伦规范洛伦兹规范2.电偶极场和电偶极辐射近区电磁场远区电磁场边界条件。

静电场和稳恒电流的相关知识1. 静电场1.1 定义静电场是指在空间中某点由于静止电荷产生的电场。

静电场的基本特性是对放入其中的电荷有力的作用。

1.2 静电场的基本方程静电场的基本方程为高斯定律，它描述了静电场与静止电荷之间的关系。

高斯定律表明，通过任何闭合曲面的电通量与该闭合曲面所包围的净电荷成正比。

1.3 电场强度电场强度是描述静电场强度的物理量，定义为单位正电荷在电场中所受到的力。

电场强度的方向与正电荷所受力的方向相同，大小与电荷所受力的大小成正比。

1.4 电势电势是描述静电场能量状态的物理量，定义为单位正电荷在电场中的势能。

电势的大小与电场中的位置有关，其方向从高电势指向低电势。

1.5 静电场的能量静电场的能量是指静止电荷在静电场中的势能总和。

静电场的能量与电荷的分布和电势有关。

2. 稳恒电流2.1 定义稳恒电流是指在电路中电流的大小和方向不随时间变化的电流。

稳恒电流的形成条件是电路中的电压源和电阻保持不变。

2.2 欧姆定律欧姆定律是描述稳恒电流与电压、电阻之间关系的定律。

欧姆定律表明，在稳恒电流条件下，电流的大小与电压成正比，与电阻成反比。

2.3 电阻电阻是描述电路对电流阻碍作用的物理量。

电阻的大小与材料的种类、形状和温度有关。

2.4 电路的基本元件电路的基本元件包括电源、导线、电阻、电容和电感。

这些元件共同决定了电路中的电流、电压和能量传输。

2.5 稳恒电流的计算稳恒电流的计算可以通过欧姆定律和基尔霍夫定律进行。

基尔霍夫定律包括电流定律和电压定律，用于描述电路中电流和电压的分布。

3. 静电场和稳恒电流的关系3.1 静电场的产生静电场的产生是由于电荷的分布和运动。

当电荷静止时，产生的电场为静电场；当电荷运动时，产生的电场为磁场。

3.2 稳恒电流的磁场稳恒电流在空间中产生的磁场为圆形磁场，其大小与电流的大小和距离有关。

稳恒电流的磁场与静电场无关。

3.3 静电场和稳恒电流的相互作用静电场和稳恒电流之间存在相互作用。

稳恒磁场的高斯定理
稳恒磁场的高斯定理：∮EdS=(∑Q)/ε0，稳恒电场（steady electric field）就是不随时间变化的电场，在稳恒情况下，一切物理量都不随时间变化，电荷分布当然也是如此。

从这个意义上说，稳恒电场同静电场相同，静电场所遵从的基本规律（高斯定理和安培环路定理）在稳恒电场中仍然成立。

但是静电场除了要求电荷分布不随时间变化外，还要求电荷不流动。

磁场的高斯定理反映的是磁场的性质是无源场，而安培环路定理反映的是磁场的性质是有旋场（漩涡场或非保守力场），而这又能提现静电场是有源场。

高斯定理是穿过任意闭合曲面的总磁通量必为零；环路定理是在真空中的稳恒电流磁场中，磁感应强度B沿任意闭合曲线L的线积分等于穿过这个闭合曲线的所有电流强度的代数和的μ0倍。

高斯定理反映稳恒磁场是一种有源场的性质，环路定理放映稳恒磁场是一种非保守力。

有源场.高斯定理说明电场线只能始于正电荷（或无穷远）,终于负电荷（或无穷远）,即静电场是有源场。

静电场和稳恒磁场的比较[摘要][关键词]静电场电介质电场强度电通量高斯定理电场力的功电势导体电容电流电动势磁场磁感应强度安培环路定理磁介质在运动电荷周围，不但存在电场，而且还存在磁场。

稳恒电流产生的磁场是不随时间变化的，称为稳恒磁场。

稳恒磁场和静电场是两种性质不同的场，但在研究方法上有很多相似的地方，下面我们来比较：静电场是相对于观察者为静止的带电体周围存在的电场。

电场是一种特殊形态的物质，其物质性一方面体现在它的带电体的作用力，以及带电体在电场中运动时电场力对带电体做功；另一方面体现在电场具有能量。

动量和电磁质量等物质的基本属性。

电场强度和电动势是描述电场特性的两个物理量。

高斯定理和场强环流定理是反应静电场和稳恒电场性质的基本规律。

在电场作用下，导体和电介质的电荷分布会发生变化，这种变化了的电荷分布又会反过来影响电场分布，最后达到平衡。

稳恒磁场就是稳定的电流周围的磁场。

稳恒电流的磁场真空中的磁场主要分为两部分:一是电流激发的磁场;二是磁场对电流的作用。

稳恒电流激发静磁场,磁场是电场的相对论效应，若空间不止一个运动电荷,则空间某点总磁感应强度等于各场源电荷单独在该点激发的磁感应强度的矢量和。

运动的电荷产生磁场。

性质根据静电场的高斯定理，静电场的电场线起于正电荷或无穷远,终止于负电荷或无穷远，故静电场是有源场．从安培环路定理来说它是一个无旋场．根据环量定理，静电场中环量恒等于零,表明静电场中沿任意闭合路径移动电荷，电场力所做的功都为零，因此静电场是保守场．根据库仑定律，两个点电荷之间的作用力跟它们的电荷量的乘积成正比，和它们距离的平方成反比，作用力的方向在它们的连线上，即Ｆ＝kq1q2/r,其中q1、q2为两电荷的电荷量、k为静电力常量，约为9.0e+09牛顿米2/库2，r为两电荷中心点连线的距离。

注意，点电荷是当带电体的距离比它们的大小大得多时，带电体的形状和大小可以忽略不计的电荷．静电感应如果电场中存在导体，在电场力的作用下出现静电感应现象,使原静电场来中和的正、负电荷分离,出现在导体表面上。

静电场和稳恒电流场的异同
静电场和稳恒电流场都是电场的一种，它们的共同点是都由电荷所产生，都遵循库仑定律。

但是它们的不同之处也很明显。

首先，静电场是指没有电流存在的电场，即电荷在空间中的分布所形成的电场。

而稳恒电流场则是指电流在导体中稳定流动所形成的电场。

因此，稳恒电流场中必然存在电流，而静电场中则没有电流。

其次，由于静电场中没有电流，因此在静电场中电场强度只与电荷的分布有关，而与时间无关。

而在稳恒电流场中，电场强度不仅与电荷的分布有关，还与电流的大小和方向有关，因此随着电流的变化而变化。

最后，由于稳恒电流场中存在电流，因此它会产生磁场，而静电场则不会。

这是电场和磁场之间的关系，也是电磁场理论的基础之一。

综上所述，静电场和稳恒电流场在电场的产生、电场强度和与磁场的关系上都存在差异，但它们都是电场的一种，都遵循库仑定律。

- 1 -。

电磁场分类
电磁场是物理学中的一个重要概念，它是由电荷和电流所产生的一种物理场。

根据电磁场的性质和特点，可以将其分为静电场、恒定磁场和电磁波三种类型。

静电场是指在没有电流的情况下，由电荷所产生的电场。

在静电场中，电荷之间的相互作用力是通过电场传递的。

静电场的特点是稳定、静止和不可逆转。

静电场的应用非常广泛，例如电荷分离、电场感应、电容器等。

恒定磁场是指在没有电荷的情况下，由电流所产生的磁场。

在恒定磁场中，电流之间的相互作用力是通过磁场传递的。

恒定磁场的特点是稳定、静止和不可逆转。

恒定磁场的应用也非常广泛，例如电动机、发电机、电磁铁等。

电磁波是指由电场和磁场相互作用所产生的一种波动现象。

电磁波的特点是具有波动性、传播性和相互作用性。

电磁波的应用非常广泛，例如无线电通信、雷达、微波炉等。

电磁场是物理学中非常重要的一个概念，它的分类有助于我们更好地理解和应用电磁场的知识。

静电场、恒定磁场和电磁波分别具有不同的特点和应用，我们需要根据实际情况选择合适的电磁场类型进行研究和应用。