叠加地震记录的相移波动方程正演模拟数值模拟实验共22页

地震波波动方程数值模拟方法地震波波动方程数值模拟方法主要包括克希霍夫积分法、傅里叶变换法、有限元法和有限差分法等。

克希霍夫积分法引入射线追踪过程，本质上是波动方程积分解的一个数值计算，在某种程度上相当于绕射叠加。

该方法计算速度较快，但由于射线追踪中存在着诸如焦散、多重路径等问题，故其一般只能适合于较简单的模型，难以模拟复杂地层的波场信息。

傅里叶变换法是利用空间的全部信息对波场函数进行三角函数插值，能更加精确地模拟地震波的传播规律，同时，利用快速傅里叶变换(FFT)进行计算，还可以提高运算效率，其主要优点是精度高，占用内存小，但缺点是计算速度较慢，对模型的适用性差，尤其是不适应于速度横向变化剧烈的模型.波动方程有限元法的做法是：将变分法用于单元分析，得到单元矩阵，然后将单元矩阵总体求和得到总体矩阵，最后求解总体矩阵得到波动方程的数值解；其主要优点是理论上可适宜于任意地质体形态的模型，保证复杂地层形态模拟的逼真性，达到很高的计算精度，但有限元法的主要问题是占用内存和运算量均较大，不适用于大规模模拟，因此该方法在地震波勘探中尚未得到广泛地应用。

相对于上述几种方法，有限差分法是一种更为快速有效的方法。

虽然其精度比不上有限元法，但因其具有计算速度快，占用内存较小的优点，在地震学界受到广泛的重视与应用。

声波方程的有限差分法数值模拟对于二维速度-深度模型，地下介质中地震波的传播规律可以近似地用声波方程描述：)()(2222222t S zu x u v t u +∂∂+∂∂=∂∂ （4-1） (,)v x z 是介质在点（x , z ）处的纵波速度，u 为描述速度位或者压力的波场，)(t s 为震源函数。

为求式（4-1）的数值解，必须将此式离散化，即用有限差分来逼近导数，用差商代替微商。

为此，先把空间模型网格化（如图4-1所示）。

设x 、z 方向的网格间隔长度为h ∆，t ∆为时间采样步长，则有：z∆,i j1,i j +2,i j+1,i j-h i x ∆= （i 为正整数）h j z ∆= (j 为正整数)t n t =∆ (n 为正整数)k j i u , 表示在(i,j)点，k 时刻的波场值。

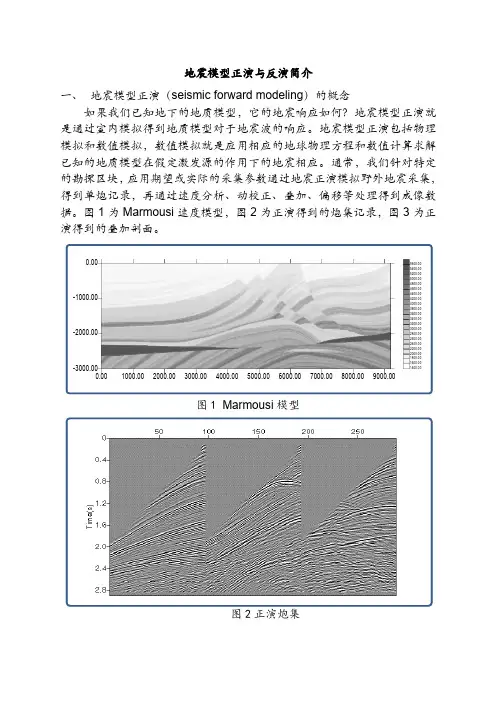
地震模型正演与反演简介一、地震模型正演（seismic forward modeling）的概念如果我们已知地下的地质模型，它的地震响应如何？地震模型正演就是通过室内模拟得到地质模型对于地震波的响应。

地震模型正演包括物理模拟和数值模拟，数值模拟就是应用相应的地球物理方程和数值计算求解已知的地质模型在假定激发源的作用下的地震相应。

通常，我们针对特定的勘探区块，应用期望或实际的采集参数通过地震正演模拟野外地震采集，得到单炮记录，再通过速度分析、动校正、叠加、偏移等处理得到成像数据。

图1为Marmousi速度模型，图2为正演得到的炮集记录，图3为正演得到的叠加剖面。

图1 Marmousi模型图2正演炮集图3 正演叠加剖面二、数值模型正演方法通常，我们提到的模型正演为数值模拟的模型正演，目前常用的数值模拟地震模型正演方法包括基于射线原理的射线追踪法，以及基于波动方程的有限差分法、有限元法、积分方程法、快速傅里叶变换法和拟谱法等。

射线追踪法主要反映地震波的运动学特征，有限差分、有限元法则适合复杂地质构造的正演模拟，积分方程法涉及复杂的数学推导，快速傅里叶变换法在频率域计算得到正演数据。

三、数值模型正演的步骤数值模拟求解地震模型正演问题的步骤主要包括以下三个方面：1) 地质建模，根据研究对象和问题建立地球物理或地质模型；2) 数学建模，根据应用的物理手段和地球物理模型建立相应的数学模型；3) 模拟计算，选择正演计算方法，编写计算程序进行数值模拟计算。

四、什么是地震反演地震反演技术就是充分利用测井、钻井、地质资料提供的丰富的构造、层位、岩性等信息，从常规的地震剖面推导出地下地层的波阻抗、密度、速度、孔隙度、渗透率、沙泥岩百分比、压力等地球物理信息。

反演就是由地震数据得到地质模型，进行储层、油藏研究。

地震资料反演可分为两部分：1）通过有井(绝对)、无井（相对）波阻抗反演得到波阻抗、速度数据体。

2）利用测井、测试资料结合波阻抗、速度数据进行岩性反演，得到孔隙度、渗透率、砂泥百分比、压力等物理数据。

《地震数值模拟》实验报告一、实验题目叠加地震记录的相移波动方程正演模拟二、实验目的1.掌握各向同性介质任意构造、水平层状速度结构地质模型的相移波动方程正演模拟基本理论2.实现方法与程序编制3.由正演记录初步分析地震信号的分辨率。

三、实验原理1、地震波传播的波动方程设（x,z）为空间坐标，t为时间，地震波传播速度为v(x,z)，则二位介质中任意位置、任意时刻的地震波场为p(z,x,t)：压缩波——纵波。

则二维各向同性均匀介质中地震波传播的遵循声波方程为2、傅里叶变换的微分性质p(t)与其傅里叶变换的P(w)的关系：3、地震波传播的相移外推公式令速度v不随x变化，只随z变化，则利用傅里叶变换微分性质把波动方程(变换到频率-波数域，得：4、初始条件和边界条件按照爆炸界面理论，反射界面震源在t=0时刻同时起爆，此时刻的波场就是震源。

根据不同情况，可直接使用反射系数脉冲或子波作震源。

如果直接使用反射系数作震源脉冲，则初始条件可表示为：5、边界处理（1）边界反射问题把实际无穷空间区域中求解波场的问题化为有穷区域求解时，左右两边使用零边界条件。

物理上假设探区距Xmin与Xmax两个端点很远，在两个端点上收到的反射波很弱。

但是，上述条件在实际中不能成立，造成零边界条件反而成为绝对阻止波通过的强反射面。

在正演模拟的剖面上出现了边界假反射干涉正常界面的反射。

（2）边界强反射的处理镶边法、削波法、吸收边界都能有效消除边界强反射。

削波法就是在波场延拓过程中，没延拓一次，在其两侧均匀衰减到零，从而消除边界强反射的影响。

假设横向总长度为NX，以两边Lx道吸波为例，有以下吸波公式：四、实验内容1、基本要求（1）点绕射构造和水平层状速度模型（参数如图1所示）的正演数值模拟；五、实验步骤1、参数初始化；2、形成边界削波数据；3、波场初始化；4、Zmax层波场延拓到深度Zmax-1；5、Zi+1层波场延拓到深度Zi；6、重复5，从Iz=Nz-1开始，直到Iz=1，得测线上的频率—空间域波场；7、频率-空间域波场对频率做反傅里叶变换，得时间-空间波场；8、使用Fimage软件显示所得结果。

一、实验题目地震记录数值模拟的这几模型法 二、实验目的掌握褶积模型基本理论、实现方法与程序编制，由褶积模型初步分析地震 信号的分辨率问题 三、实验原理 1、褶积原理地震勘探的震源往往是带宽很宽的脉冲，在地下传播、反射、绕射到测线，传播经过中 高频衰减，能量被吸收。

吸收过程可以看成滤波的过程，滤波可以用褶积完成。

在滤波中， 反射系数与震源强弱关联，吸收作用与子波关联。

最简单的地震记录数值模拟，可以看成反 射系数与子波的褶积。

通常，反射系数是脉冲，子波取雷克子波。

（1） 雷克子波Wave(t) = (1−2π2f 2t 2)e −2π2f 2t 2（2）反射系数：rflct(z)=1 z =z 反射界面0 z =others（3）褶积公式： 数值模拟地震记录trace(t): trace(t) =rflct(t)*wave(t)反射系数的参数由z 变成了t ，怎么实现？在简单水平层介质，分垂直和非垂直入射两 种实现，分别如图1 和图2 所示。

1） 垂直入射：t =2h v图一垂直入射2） 非垂直入射：t =2 h 2+x 2v图二非垂直入射2、褶积方法（1）离散化（数值化）计算机数值模拟要求首先必须针对连续信号离散化处理。

反射系数在空间模型中存在，不同深度反射系数不同，是深度的 函数。

子波是在时间记录上一延续定时间的信号，是时间的概念。

在离散化时，通过深度采 样完成反射系数的离散化，通过时间采样完成子波的离散化。

如果记录是Trace(t)，则记录 是时间的函数，以时间采样离散化。

时间采样间距以∆t 表示，深度采样间距以∆z 表示。

在 做多道的数值模拟时，还有横向x 的概念，横向采样间隔以∆x 表示。

离散化的实现：t=It×∆t ；x=Ix×∆x ；z=Iz×∆z或：It=t/∆t; Ix=x/∆x; Iz=z/∆z （2）离散序列的褶积 trace It = rflct(Itao) ×wave(It −Itao)∞Itao =−∞ 四、实验内容1、垂直入射地震记录数值模拟的褶积模型；2、非垂直入射地震记录数值模拟的褶积模型；3、点绕射的地震记录数值模拟的褶积模型；五、方法路线根据褶积模型的实验原理编写C++程序，完成对于垂直入射波的褶积。

第1篇一、实验背景地震作为一种自然灾害，给人类带来了巨大的生命财产损失。

为了提高人们对地震的认识和应对能力，我们进行了模拟地震演示实验。

本次实验旨在通过模拟地震现象，让学生直观地了解地震成因、传播过程及地表变化，增强他们的防灾减灾意识。

二、实验目的1. 了解地震成因及传播过程；2. 熟悉地震波对地表的影响；3. 增强学生的防灾减灾意识。

三、实验原理地震是地壳内部岩石层在内外力作用下发生变形或断裂，产生的地震波传到地表引起地表震动的过程。

本实验采用模拟地震的方法，通过搭建模拟地震装置，模拟地震成因、传播过程及地表变化。

四、实验器材1. 模拟地震装置：由支架、模型岩石层、弹簧、传感器等组成；2. 计时器；3. 地震波记录仪；4. 地表模型；5. 地震波模拟软件。

五、实验步骤1. 搭建模拟地震装置：将支架固定在地面上，将模型岩石层放置在支架上，将弹簧连接在岩石层两端，确保弹簧处于拉伸状态；2. 连接传感器：将传感器安装在岩石层上，连接地震波记录仪；3. 地震波模拟：启动地震波模拟软件，模拟地震波传播过程；4. 观察现象：观察岩石层变形、弹簧伸缩、传感器数据变化及地表模型变化；5. 记录实验数据：记录岩石层变形程度、弹簧伸缩长度、传感器数据及地表模型变化情况。

六、实验结果与分析1. 实验结果显示，模拟地震装置在地震波模拟软件的驱动下，岩石层发生了变形，弹簧伸缩，传感器数据发生明显变化，地表模型也发生了相应的变化；2. 通过实验数据，可以得出以下结论：（1）地震波在传播过程中，会使得岩石层发生变形，弹簧伸缩，导致地表发生变化；（2）地震波传播速度与岩石层性质、地震波频率等因素有关；（3）地震波传播过程中，能量逐渐衰减，地表变化程度与地震波传播距离有关。

七、实验总结本次模拟地震演示实验，使学生直观地了解了地震成因、传播过程及地表变化，提高了他们的防灾减灾意识。

实验过程中，学生积极参与，认真观察，对地震现象有了更深入的认识。

图３－１四川盆地邛西ｑｘ４井区域无裂缝岩性构造剖面模型及层速度分布图３—２四川盆地邛西ｑｘ４井区域无裂缝岩性构造地质模型的地震正演（ｐｓｐｚｔ＝３３５０ｍ．ｖｌ＝３８００ｍ／ｓ．ｄｘ＝２５ｍ，ｄｚ＝４ｍ．８０×１２８）其中ｐｓｐｉ代表纵横向速度可变的波场延拓方法，ｐｓ代表纵向速度可变的波场延拓方法，ｚ１表示模型的其始深度，ｄ）【为道间距（米），ｄｚ为深度延拓步长（米）（以下同）。

图３＿３四川盆地邛西Ｏｘ４井区域无裂缝地质构造模型记录的偏移剖面（ｐｓｐｚ１＝３３５０ｍ．ｖｌ＝３８００ｍ／ｓ，ｄｘ＝２５ｍ．ｄｚ＝４ｍ．８０ｘ１２８）图３－４四川盆地邛西ｑｘ４井区域无裂缝地质构造模型加密型（ｄｘ，ｄｚ缩减一倍）的偏移剖面（ｐｓｐｉ．ｚｌ＝３３５（）ｌａ，ｖｌ＝３８００ｍ／ｓ，ｄｘ＝１２．５ｍ．ｄｚ＝２Ｊｎ．１６０ｘ２５６）图３—３和图３－４的偏移剖面中，均能清晰地分辨出地层、岩性和构造、断层存在的空间位置，也能可靠地分辨出薄层，能与原始地质模型图３－１全面对比，说明波动方程正演和偏移的质量正确、可靠，在此基础上做裂缝模拟具有良好的条件。

偏移剖面中，界面的台阶形状是与离散采样后的输入地质剖面一致的，这进一步说明所用正演和偏移方法的高质量。

（２）有裂缝的复杂岩性构造模型（裂缝带在图中部透镜体之下）裂缝充填物的性质由裂缝带的散射系数确定，散射系数大，代表充填物为流体，散射系数小，代表充填物为刚性系数大的物质，散射系数的正负，由充填物和围岩之间的性质决定。

下面分别采用了０．２，０．０５和．０．１０的散射系数。

图３＿５四川盆地邛西ｑｘ４井区域有裂缝地质构造模型及层速度分布（裂缝等效散射系数０．２）圈３－６四川盆地邛西ｑｘ４井区域裂缝地质构造模型正演（ｐｓｐｉ．ｚｌ＝３３５０ｍ．ｖｌ＝３８００ｎＶｓ，ｄｘ＝２５ｍ．ｄｚ＝４ｍ．８０×１２８裂缝散射系数０．２）图３－７ＰＯＩＩＩ盆地邛西ｑｘ４并区域裂缝地质构造模型正演（ｐｓ，ｚ１＝３３５０ｍ，ｖ１＝３８００ｍ／ｓ．ｄｘ＝２５ｍ。

地震模型正演与反演简介一、地震模型正演（seismic forward modeling）的概念如果我们已知地下的地质模型，它的地震响应如何？地震模型正演就是通过室内模拟得到地质模型对于地震波的响应。

地震模型正演包括物理模拟和数值模拟，数值模拟就是应用相应的地球物理方程和数值计算求解已知的地质模型在假定激发源的作用下的地震相应。

通常，我们针对特定的勘探区块，应用期望或实际的采集参数通过地震正演模拟野外地震采集，得到单炮记录，再通过速度分析、动校正、叠加、偏移等处理得到成像数据。

图1为Marmousi速度模型，图2为正演得到的炮集记录，图3为正演得到的叠加剖面。

图1 Marmousi模型图2正演炮集图3 正演叠加剖面二、数值模型正演方法通常，我们提到的模型正演为数值模拟的模型正演，目前常用的数值模拟地震模型正演方法包括基于射线原理的射线追踪法，以及基于波动方程的有限差分法、有限元法、积分方程法、快速傅里叶变换法和拟谱法等。

射线追踪法主要反映地震波的运动学特征，有限差分、有限元法则适合复杂地质构造的正演模拟，积分方程法涉及复杂的数学推导，快速傅里叶变换法在频率域计算得到正演数据。

三、数值模型正演的步骤数值模拟求解地震模型正演问题的步骤主要包括以下三个方面：1) 地质建模，根据研究对象和问题建立地球物理或地质模型；2) 数学建模，根据应用的物理手段和地球物理模型建立相应的数学模型；3) 模拟计算，选择正演计算方法，编写计算程序进行数值模拟计算。

四、什么是地震反演地震反演技术就是充分利用测井、钻井、地质资料提供的丰富的构造、层位、岩性等信息，从常规的地震剖面推导出地下地层的波阻抗、密度、速度、孔隙度、渗透率、沙泥岩百分比、压力等地球物理信息。

反演就是由地震数据得到地质模型，进行储层、油藏研究。

地震资料反演可分为两部分：1）通过有井(绝对)、无井（相对）波阻抗反演得到波阻抗、速度数据体。

2）利用测井、测试资料结合波阻抗、速度数据进行岩性反演，得到孔隙度、渗透率、砂泥百分比、压力等物理数据。

地震正演模拟
1. 原理
在地震记录上看到的波形是地震子波叠加的结果，从地下许多反射界面发生反射时形成的地震子波，振幅大小决定于反射界面反射系数的绝对值，极性的正负决定于反射系数的正负，到达时间的先后取决于界面深度和覆盖层的波速。

若地震子波波形用S(t)表示，反射系数是双程垂直反射旅行时t 的函数，用R(t)表示，地震记录f(t)形成的物理过程在数学上就可表示为：
f(t)=S(t)* R(t)=∫S (t )R (t −τ)dτT
其中反射系数R 取R=ρ2v2−ρ1v1ρ2v2+ρ1v1，设地层密度为均匀的，且令ρ2=4ρ1，则反射系数只与地层间速度有关。

地震子波取雷克子波S(t)=[1-2*（pi*fp*t ）2]exp[-（pi*fp*t ）2]，其中主频取fp=20。

2. 模型
本次模拟中采用的是300*80的网格，道数为80，垂直采样点数为300。

模型为一个三层水平层状均匀介质，其速度分别为1000m/s 、2000m/s 、3000m/s ，模型如下：
图1 模型示意图 图2 地震子波 3. 结果 2000m/s 1000m/s
3000m/s
图2 各层界面的地震响应。

地震波动方程第三章地震波动方程现在，我们用前一章提出的应力和应变理论来建立和解在均匀全空间里弹性波传播的地震波动方程。

这章涉及矢量运算和复数，附录2对一些数学问题进行了复习。

3.1 运动方程（Equation of Motion）前一章考虑了在静力平衡和不随时间变化情况下的应力、应变和位移场。

然而，因为地震波动是速度和加速度随时间变化的现象，因此，我们必须考虑动力学效应，为此，我们把牛顿定律（maF ）用于连续介质。

3.1.1一维空间之振动方程式质点面上由于应力差的存在而使质点产生振动。

如图1-3所示，考虑一薄棒向x轴延伸，其位移量为u：Fig3-1则其作用力为“应力”X“其所在的质点面积”，所以其两边的作用力差为()()()dxds xx dx x ds ∂∂=-+σσσ惯量﹙inertia ﹚为22tu dxds ∂∂ρ所以得出xt u ∂∂=∂∂σρ22……………………………………………………... （3-1）其中ρ为密度﹙density ﹚，σ为应力﹙stress ﹚=xuE ∂∂。

3-1式表示，物体因介质中的应力梯度﹙stress gradient ﹚而得到加速度。

如果ρ与E 为常数，则3-1式可写为222221t uc x u ∂∂=∂∂…………………………………………………… （3-2） 其中ρEc =运用分离变量法求解（3-2）式，设u=F(x)T(t),(3-2)式可以变为T X c T X ''=''21设22ω-=''=''TT X X c则可得：cx iti eX eT ωω±±∝∝,考虑欧拉公式：)sin()cos(),sin()cos(t i t e t i t et i ti ωωωωωω-=+=-()()()()ct x cict x cict x cict x ciDeCeBeAeu ---+-++++=ωωωω （3-3）其中A,B,C,D 为根据初始条件和边界条件确定的常数。

1-1-1正演的速度模型图图1-1-2分块均匀的模型1-2正演的后的走时图图1-3 反演前后速度对比图图1-5-a第0炮，第5接收点的数据图1-5-b-1正演第1炮，第8接收点（0为开始的激发点，0开始的接收点）图1-5-b-2 与1-5-b-2对应的验证图形（附注：由于本人u盘被病毒入侵，导致本人做得CAD图丢失，此图引用廖松杰同学的CAD图像，但是1-5-b-2由本人程序自己得出，特此说明。

）图1-5-c四边放炮，四边接收左方第2激发，图1-5-b单边接收第0炮，第25接收的r图像第5接收点的r数据图正反演的程序单边放炮单边接收：#include<stdio.h>#include<stdlib.h>#include<math.h>void fun1(int n,double R[144][108],double t[12][12]);void fun2(double k,double o,double t[12][12],double R[144][108],int m,int n);//k为斜率，o为炮点坐标，相当于截距；j；double fun(double x1,double y1,double x2,double y2);void main(){FILE *fp;int i,j,m,n,l,f;doublec[12],d[12],K[12][12],r[12][9]={0},v[12][9]={0.0},t[12][12]={0.0},u,o,w,R[144][108]={0. 0},k,v2[144]={0};float v1;//******************************************************************* ************************************//for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{ v[i][j]=3000;}}v[2][2]=5000.0;v[3][2]=5000.0;v[8][5]=2000.0;v[8][6]=2000.0;for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{v2[j*12+i]=v[i][j];}}fp=fopen("速度","wb");for(i=0;i<12;i++){for(j=0;j<9;j++){v1=v[i][j];fwrite(&v1,sizeof(float),1,fp);}}fclose(fp);//******************************************************************* ************************************////************************************* 计算各点的斜率***************************************************//for(i=0;i<12;i++){//printf("第%d炮的斜率\n",i);c[i]=(i+0.5)*5.0;//*************************************************** ************激发点********//for(j=0;j<12;j++){d[j]=(j+0.5)*5;//**************************************************** *******接收点********//K[i][j]=(d[j]-c[i])/(9.0*3);//******************************************** **K斜率*********////printf("K[%d][%d]=%f\n",i,j,K[i][j]);}//printf("\n");}//******************************************************************* ***************************************//for(i=0;i<12;i++)//第i炮{for(j=0;j<12;j++)//第j接收点{if(K[i][j]==0)//平行于x轴,该行所在的每一个网格均经过,路程都是3{fun1(i,R,t);printf("t[%d][%d]=%f\n",i,j,t[i][j]);}else if(K[i][j]!=0){k=K[i][j];o=c[i];m=i;n=j;fun2(k,o,t,R,i,j);printf("t[%d][%d]=%lf\n",i,j,t[i][j]);}}}fp=fopen("time.txt","w");for(i=0;i<12;i++){for(j=0;j<12;j++){fprintf(fp,"%lf\n",t[i][j]);}}fclose(fp);fp=fopen("系数矩阵R的值.txt","w");for(i=0;i<144;i++){for(j=0;j<108;j++){fprintf(fp,"%f\t",R[i][j]);}fprintf(fp,"\n");}fclose(fp);fp=fopen("原来的速度值.txt","w");for(j=0;j<108;j++){fprintf(fp,"%f\t",v2[j]);}fclose(fp);}//******************************************************************* ***************************************////******************************************************************* ***************************************////*******************************当斜率k为0的时候，计算走时t的值********************************************////******************************************************************* ***************************************//void fun1(int n,double R[144][108],double t[12][12]){FILE *fp1;double b=0.0;int i=0,j=0,q=0;//循环变量double r[12][9]={0.0},v[12][9];//*************************************************************** for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{ v[i][j]=3000;}}v[2][2]=5000.0;v[3][2]=5000.0;v[8][5]=2000.0;v[8][6]=2000.0;for(j=0;j<9;j++){r[n][j]=3.0;}//******************************************************************* **////**********************写出检验r的值**********************************///*fp1=fopen("r的值.txt","w");for(i=0;i<12;i++){for(j=0;j<9;j++){fprintf(fp1,"%f\t",R[i][j]);}fprintf(fp1,"\n");}fclose(fp);*///******************************************************************* ****////******************************************************************* ****//for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{b+=r[i][j]*(1/v[i][j]);}}t[n][n]=b;for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{R[n*12+n][q++]=r[i][j];}}}double fun(double x1,double y1,double x2,double y2){double s;{s=(y2-y1)*(y2-y1)+(x2-x1)*(x2-x1);return sqrt(s);}}//*****************************************************////******************************************************************* ***************************************//void fun2(double k,double o,double t[12][12],double R[144][108],int m,int n)//k为斜率，o为炮点坐标，相当于截距；{FILE *fp2;int i=0,j=0,q=0;;//循环变量int w1,w2,w3,w4;//中间变量，用来判断点在分块均匀上的位置double p=0,v[12][9]={0.0},r[12][9]={0.0};double x1,y1,x2,y2,x3,y3,x4,y4;float r1;//*************************************************************** v[2][2]=5000.0;v[3][2]=5000.0;v[8][5]=2000.0;v[8][6]=2000.0;for(i=0;i<12;i++)//第i行{for(j=0;j<9;j++)//第j列{ v[i][j]=3000;r[i][j]=0;}}for(i=0;i<12;i++){for(j=0;j<9;j++){y1=i*5.0;x1=(y1-o)/k;//计算交点1,由y计算x,交点一位于上边y2=(i+1)*5.0;x2=(y2-o)/k;//计算交点1,由y计算x，交点2位于下边x3=j*3.0;y3=k*x3+o;//计算交点3,由x计算y，交点3位于左边x4=(j+1)*3.0;y4=k*x4+o;//计算交点3,由x计算y，交点四位于右边//******************************************************************* ***//***判断射线是否经过分块均匀的网格点上,四个交点是否在网格的四条边上*****//**************************************************************** ******//***注意：网格的上下两条边y值相等,网格的左右两边x的值相等***************//**************************************************************** ******w1=(x1>=(j*3.0))&&(x1<=((j+1)*3.0))&&(y1==(i*5.0));//上方w2=(x2>=(j*3.0))&&(x2<=((j+1)*3.0))&&(y2==((i+1)*5.0));//下方w3=(y3>=(i*5.0))&&(y3<=((i+1)*5.0))&&(x3==(j*3.0));//左方w4=(y4>=(i*5.0))&&(y4<=((i+1)*5.0))&&(x4==((j+1)*3.0));//右方//**************************************************************** ******************//计算路径长度r，当有两个点存在时，有下面的六种情况。

第42卷第2期2003年6月石　油　物　探GE OPHY SIC A L PROSPECTI NG FOR PETRO LE UMV ol.42,N o.2Jun.,2003文章编号:100021441(2003)022*******地震波场数值模拟方法张永刚(中国石油化工股份有限公司科技发展部,北京100029)摘要:简要总结了地震波场数值模拟的各种方法的基本原理及其主要特点,对最近在该领域出现的一些方法和研究结果做了简要的阐述,并对比了各种方法的优缺点。

在此基础上提出了运用波动方程数值模拟作为基础,结合射线方法辅助识别波场类型,用于分析异常波的产生机理和出现特点的基本思想,这对复杂条件下的地震勘探具有指导和借鉴意义。

关键词:地震波场;数值模拟;射线追踪;有限元;伪谱法;正演模拟中图分类号:P63114+1 文献标识码:AOn numerical simulations of seismic w avefieldZhang Y onggang(Department of Science and T echnology Development,SI NOPEC,Beijing100029,China)Abstract:This paper reviews the principles and characteristics of various numerical simulations of seismic wavefield,and com2 pares the merits and defects of the simulations.S ome newly emerged methods and results are briefly discussed.The author pro2 poses to study the generation mechanism and characteristics of abnormal waves based on wave equation numerical simulation supplemented by ray tracing.K ey w ords:seismic wavefield;numerical simulation;ray tracing;finite element;pseudo2spectrum;forward m odeling 地震波场数值模拟是研究复杂地区地震资料采集、处理和解释的有效辅助手段,地震波场数值模拟的主要方法包括2大类,即波动方程法和几何射线法。