5.2任意角的三角比(1)

课题 第五章 三角比 §5.2 任意角的三角比 课时：1教者：浦东新区新场中学 刘彦 设计背景：从锐角三角比引入任意角的三角比，指出两者之间的联系与区别。

后者是前者的推广与延伸，既有相同之处，又有一定的区别。

教学实施： 一 教学目标知识与技能 掌握任意角三角比的计算公式，体会类比及数形结合思想，提高分析研究解决问题的能力。

过程与方法 从特殊到一般的研究方法，类比的方法以及从已知到未知的知识建构。

态度与情感 培养学生研究以及探究的欲望和严谨的学习态度。

二 教学重点 任意角的六个三角比的定义和三角比的符号。

教学难点 坐标系下用坐标比定义三角比的合理性的理解。

三 实施过程 1、新课引入：锐角三角比：弧度制实现了角的实数化，任意角实现了角到任意实数。

今天我们要学任意角的三角比，这与什么知识有联系？锐角的三角比。

QPOsin cos tan cot y r xr yx xyαααα====提问：如果延长斜边，然后换一个点，比值有没有变化？相似的思想。

因此锐角的三角比可以通过终边上的点的坐标来表示。

类似地我们可以得到任意角三角比的定义。

2新课讲授（1）任意角三角比：αsin (cos ()tan (,)2cot (,)sec (,)2csc (,)y r xR r y k k Z x xk k Z y r k k Z x rk k Z yαααααπααπααππααπααπ==∈=≠+∈=≠∈=≠+∈=≠∈取一切角，可得0OP r ==>引导学生得出以下结论：(1)、三角比可能为负值（为三角函数打下基础，函数值可能为负值）(2)、α取值范围（三角函数自变量的定义域）提问：是不是任意角都有三角比？三角比都有意义？看什么？看它的分母！(3)、角α的三角比与点P 在终边的位置 关。

(4)、,,x y r （任意两个量做比值）符号由x,y 决定。

（2）、例题讲解与训练：例1：已知角α终边上一点(2,1)P -，求角α的六个三角比。

任意角的三角比一、基础知识熟练记忆1、任意角的三角比——对于任意角的三角比，我们利用平面直角坐标系来进行研究。

（1）设α是一个任意角，在α的终边上任取（异于原点的）一点P （x,y ） 则点P 与原点的距离02222>+=+=y x y x r（2）比值r y叫做α的正弦 记作： r y =αsin 比值r x叫做α的余弦 记作： r x =αcos 比值x y叫做α的正切 记作： xy =αtan 比值y x叫做α的余切 记作： yx =αcot 比值x r叫做α的正割 记作： x r =αsec 比值y r叫做α的余割 记作： yr =αcsc 根据相似三角形的知识，对于终边不在坐标轴上确定的角α， 上述六个比值都不会随P 点在α的终边上的位置的改变而改变。

当角α的终边在纵轴上时，即Z)(2∈+=k k ππα时，终边上任意一点P 的横坐标x 都为0，所以tan α、sec α无意义；当角α的终边在横轴上时，即α＝ｋπ（ｋ∈Z ）时， 终边上任意一点P 的纵坐标ｙ都为0，所以cot α、csc α无意义。

几个需要注意的问题：① 凡是终边相同的角的三角函数值相等。

sin(2k π+α)=sin α cos(2k π+α)=cos α tan(2k π+α)=tan α cot(2k π+α)=cot α② 0>r 而x,y 的正负是随象限的变化而不同，故三角函数的符号应由象限确定。

第一象限：0,0.>>y x∴sin α>0，cos α>0，tan α>0，cot α>0 第二象限：0,0.><y x∴sin α>0，cos α<0，tan α<0，cot α<0O A M P Txyα的终边 x yO A M T yOAM xyOAM TPα的终边第三象限：0,0.<<y x∴sin α<0，cos α<0，tan α>0，cot α>0 第四象限：0,0.<>y x∴sin α<0，cos α>0，tan α<0，cot α<0记忆法则：第一象限全为正，二正三切四余弦。

5.2三角比定义：设角α是一个任意角，将角α角α的顶点与原点O 重合，α的始边与x 在α的终边上任取（异于原点的）一点P （x,y ）, 有点P 到原点的距离 2222+=+=y x yx r 则我们规定：sin ,cos ,()y xR r rααα==∈tan ,(,)2y k k Z x πααπ=≠+∈ ；cot (x y αα=sec ,(,)2r k k Z x πααπ=≠+∈ csc (,)r k k Z yααπ=≠∈。

诱导公式：第一组（2k πα+）：sin(2)sin k παα+=， cos(2)cos k παα+=，tan(2)tan k παα+=；【典型例题】 ［例1］(1)设(,)63ππθ∈，且17θ的终边与θ角的终边相同，则tan θ＝____(2)如果θ是第一象限角，那么①sin02θ>,②tan12θ<,③sincos22θθ>,④sincos22θθ<中恒成立的有_____个。

(3) .若tan α＝3，则ααααsin 3cos 5cos 2sin 4+-=_______(4)已知扇形的半径为10㎝，圆心角为120°，则扇形的弧长为 ；面积为 ． (5)已知04sin(540),cos(270)5αα+=--=则 ． ［例2］若tan α=1）sin cos cos sin αααα+-的值；（2）222sin sin cos cos αααα-+的值．［例3］若1sin cos ,,,cos sin 842ππθθθθθ⎛⎫=∈- ⎪⎝⎭求的值．［例4］已知sin()cos(2)tan(3)2()tan()sin()2f παπααπαππαα---+=++．（1） 化简()f α；（2） 若α是第三象限的角，且31cos()25πα-=，求()f α的值； （3） 若01860α=-，求()f α的值．1cos(6360300)cos602=--⨯+=-=-【练习】1．34sin ,cos ,255θθθ=-=若则角的终边在第_______象限 ２．已知sin 1,cos 43k k θθ=-=-，且θ是第二象限角，则k 应满足的条件是______. ３．已知1sin 1cos ,cos 2sin 1x xx x +=--那么=_________ ４．设θ是第三象限角，且coscos ,222θθθ=-则是第_______象限的角５．函数()f x 满足14(cos )(0),(sin )23f x x x f ππ=≤≤=则 ． ６．若角α和β的终边关于直线0x y +=对称，且3πα=-，则β角的集合是 ；７．已知 211tan ,32sin cos cos αααα=-=+则．８．已知角θ的终边经过点P ()(0),sin m m θ≠=且，试判断角θ所在的象限，并求cos tan θθ和的值．９．已知：α是三角形的内角，若1sin cos ,tan 5ααα+=求的值．10．已知关于x 的方程4x 2－2(m +1)x +m =0的两个根恰好是一个直角三角形的两个锐角的余弦，求实数m 的值．【课后巩固】１．若θθθ则角且,02sin ,0cos <>的终边所在象限是第_______象限２．y =|sin |cos |tan |sin |cos |tan x x x x x x++的值域是________３．若f (cos x )=cos2x ，则f (sin15°)=________４．计算 7231113sin cos()tan()cos 3643ππππ-+-= ． 答：54提示：利用诱导公式 ５．已知角α的终边上一点Ｐ与点Ａ(3,2)-关于ｙ轴对称，角β的终边上一点Ｑ与点Ａ关于原点对称，那么sin sin αβ+的值等于 ．６．已知sin （3π＋θ）＝41，求)cos()cos()2cos()2cos(]1)[cos(cos )cos(θθππθπθθπθθπ-+++-+-++的值．７．如果角α的终边经过点M （1，3），试写出角α的集合A ，并求集合A 中最大的负角和绝对值最小的角.８．已知tan α是方程2210cos x x α+⋅+=的两个根中较小的根，求α的值．参考答案：例1：（1）答：1 提示: 与α角终边相同的角的集合是 }{2,k k Z ββπα=+∈ （2）答：1 提示:利用三角函数线知②总成立.（3）答：75提示:用公式sin tan cos ααα=（4）答：203π㎝ , 1003π㎝2提示:利用弧长公式l r α=及扇形面积公式12S lr =,注意圆心角的单位化为弧度 （5）答：45-提示：利用诱导公式 例2：解（1）cos sin 1tan 3cos sin 1tan αααααα++===----（2）原式2222222sin sin cos cos 2tan tan 1sin cos tan 1ααααααααα-+-+==++==例3：解：222(cos sin )cos sin 2sin cos θθθθθθ-=+-13144=-=,,cos sin 42cos sin 2ππθθθθθ⎛⎫∈∴< ⎪⎝⎭∴-=-例4、解：（1）cos cos (tan )()cos tan cos f ααααααα-==-（2）3cos()sin 2παα-=-1sin ,5αα∴=-又是第三象限的角()f αα∴===cos （3）0186********α=-=-⨯+ 0()(1860)cos(1860)f f α∴=-=-- 练习：1、答：四. 提示；由24sin 22sin cos 0,25θθθ==-< 227cos 2cos sin 025θθθ=-=>，可得 2、答：85k =. 提示：由22sin 0,cos 0sin cos 1θθθθ><+=及可得． 3、答：12. 提示：221sin sin 1sin 11cos cos cos x x x x x x +--⋅==- 4、答：二. 提示：由设θ是第三象限角知2θ是第二、四象限角，再由cos 02θ≤可得 5、答：512π 提示：455sin sin()cos3266ππππ=+= 6、答：2,6k k Z πββπ⎧⎫=-∈⎨⎬⎩⎭提示：由对称性知，β角的终边与6π-的终边相同7、答：103提示：将分子１写成 221sin cos αα=+ 然后用弦化切可得 8、解：由题意，得0,4r m m ==≠∴=故角θ是第二或第三象限角．当m =,r =P的坐标为(，cos tan x y r x θθ∴======当m =,r =P的坐标为(，cos tan x y r x θθ∴======9、解；由22sin cos 11sin cos 5αααα⎧+=⎪⎨+=⎪⎩ 解得4sin 53cos 5αα⎧=⎪⎪⎨⎪=-⎪⎩ 或3sin 54cos 5αα⎧=-⎪⎪⎨⎪=⎪⎩(0,),sin 0απα∈∴> 所以 4sin 53cos 5αα⎧=⎪⎪⎨⎪=-⎪⎩所以 sin 4tan cos 3ααα==-10、解：设直角三角形的两个锐角分别为α、β，则可得α+β=2π， ∴cos α=sin β∵方程4x 2－2(m +1)x +m =0中，Δ=4（m +1)2－4·4m =4(m －1)2≥0 ∴当m ∈R ，方程恒有两实根.又∵cos α+cos β=sin β+cos β=21+m ，cos α·cos β=sin βcos β=4m∴由以上两式及sin 2β+cos 2β=1，得1+2·4m =(21+m )2解得m =±3当m =3时，cos α+cos β=213+＞0，cos α·cos β=43＞0，满足题意， 当m =－3时，cos α+cos β=231-＜0，这与α、β是锐角矛盾，应舍去. 综上，m =3 课后巩固：1、答：四. 提示：cos 0,sin 22sin cos 0θθθθ>=<且可得2、答：{－1,3} 提示：讨论角ｘ在四个象限的情况3、答：－23 提示：00sin15cos75= 4、答：sin2+cos2.提示：2212sin(2)cos(2)sin 2cos 22sin 2cos 2ππ-++=++2(sin 2cos 2)=+及sin 2cos20+>可得5、答：０ 提示：由题设条件求出点Ｐ、点Ｑ的坐标，从而依正弦函数的定义求sin α、sin β6、解： sin （3π＋θ）＝－sin θ， ∴sin θ＝－41原式＝θθθθθθθcos )cos (cos cos )1cos (cos cos +-+---＝θθcos 11cos 11-++ ＝θθ22sin 2cos 12=-＝32 7、解：在0°到360°范围内，由几何方法可求得α=60°.∴A ={α|α=60°+k ·360°，k ∈Z }其中最大的负角为－300°（当k =－1时） 绝对值最小的角为60°（当k =0时）8、 解：由题意知：22tan tan 10cos ααα+⋅+=，解得1sin 2α=-，故cos 2α=±01 当cos α=240x ++=，解之得12x x ==故tan α=，所以2,3k k Z παπ=+∈02当cos α=240x -+=，解之得12x x ==故tan α=，所以,6k k Z παπ=+∈。

三角比知识复习5.1任意角及其度量（1）知识要点归纳：1．正角的定义：2．负角的定义：3．零角的定义：4．象限角的定义：5．角的终边在坐标轴上，这个角就（填“属于”或“不属于”）任何象限。

6．与α角终边重合的角（包括α角）β所构成的集合为7．写出终边与下列各边重合的角的集合：①x轴正半轴：②x轴负半轴：③x轴：④y轴正半轴：⑤y轴负半轴：⑥y轴：⑦坐标轴：⑧第一象限角平分线：⑨第三象限角平分线：⑩一、三象限角平分线：（11）每一个象限的角平分线________________________________________________ 8．分别写出一、二、三、四象限角的范围：①第一象限：_________________________________________________________________②第二象限：_________________________________________________________________③第三象限：_________________________________________________________________④第四象限：_________________________________________________________________5.1任意角及其度量（2）知识要点归纳：1．角度制定义：2．弧度制定义：3．弧长为l ，半径为r ，l 所对的圆心角为α，那么 （填这三者的关系） 4．弧度制与角度制的换算：1弧度= ≈ ； 1= ≈ ；= 180 ；=360 ；5．弧度制的意义：弧长与半径的比值是实数，即每个用弧度制表示的角都可以与一个 一一对应， 与实数集R 之间建立起一一对应的关系。

6．设扇形的圆心角为()παα<<0 ，半径为r ，弧长为l ，面积为S ，则：=l ； =S =5.2任意角的三角比知识要点归纳：1．任意角的三角比定义：设角的终边上有一点P(x,y),则=αsin =αcos =αtan =αcot =αsec =αcsc2．任意角α的三角比的符号及终边落在坐标轴上的特殊角的三角比： （1）三角比 第一象限 第二象限 第三象限 第四象限 sin α cos α tan α（2）α2ππ23π αsinαcosαtan αcotαsec αcsc3．单位圆定义： ； 单位圆上任一点坐标为 （用α表示）；5.3同角三角比的关系和诱导公式知识要点归纳： 1．同角三角比的关系：倒数关系：（1） ; (2) ; (3) ; 商数关系：(1) ; (2) ; 平方关系：(1) ; (2) ; (3) ; 2．诱导公式：()=+απk 2sin ; ()=+απk 2cos ;()=+απk 2tan ; ()=+απk 2cot ; （其中Z k ∈） ()=-αsin ; ()=-αcos ; ()=-αtan ; ()=-αc o t ; ()=+απsin ; ()=+απcos ; ()=+απtan ; ()=+απcot ; ()=-απsin ; ()=-απcos ; ()=-απtan ; ()=-απcot ; ()=-απ2sin ;()=-απ2cos ; ()=-απ2tan ;()=-απ2cot ;5.4两角和与差的余弦、正弦和正切（1）知识要点归纳： 1．两角和与差的三角比公式：()=+βαsin ; ()=-βαsin ; ()=+βαcos ; ()=-βαcos ;角的组合，如：（)(βα+___α=β;2)(βαα+=____)(βα-等； 2．诱导公式：=⎪⎭⎫ ⎝⎛-απ2sin ;=⎪⎭⎫ ⎝⎛-απ2cos ;=⎪⎭⎫ ⎝⎛-απ2tan ; =⎪⎭⎫⎝⎛-απ2cot ;=⎪⎭⎫ ⎝⎛+απ2sin ; =⎪⎭⎫ ⎝⎛+απ2cos ;=⎪⎭⎫ ⎝⎛+απ2tan ;=⎪⎭⎫⎝⎛+απ2cot ;=⎪⎭⎫ ⎝⎛+απ23sin ;=⎪⎭⎫ ⎝⎛+απ23cos ;=⎪⎭⎫ ⎝⎛+απ23tan ;=⎪⎭⎫⎝⎛+απ23cot ; =⎪⎭⎫ ⎝⎛-απ23sin ;=⎪⎭⎫ ⎝⎛-απ23cos ;=⎪⎭⎫ ⎝⎛-απ23tan ;=⎪⎭⎫ ⎝⎛-απ23cot ;5.4两角和与差的余弦、正弦和正切（2）知识要点归纳： 1．两角和与差的正切公式：()=+βαtan ; ()=-βαtan说明：βα 、和βα±的值都不能为注意公式的变形，如： 2．辅助角公式：（1）=+ααcos sin b a ，其中ϕ由=ϕcos ，=ϕsin ，πϕ20<≤确定（2）=+ααcos sin b a ，其中ϕ由=ϕsin ，=ϕcos ，πϕ20<≤确定5.5二倍角与半角的正弦、余弦和正切（1）知识要点归纳： 1．二倍角公式：=α2sin=α2cos = = =α2tan （ ）注：对二倍角要灵活理解，如2βα-的二倍角为 ，απ-4的二倍角为 等等。

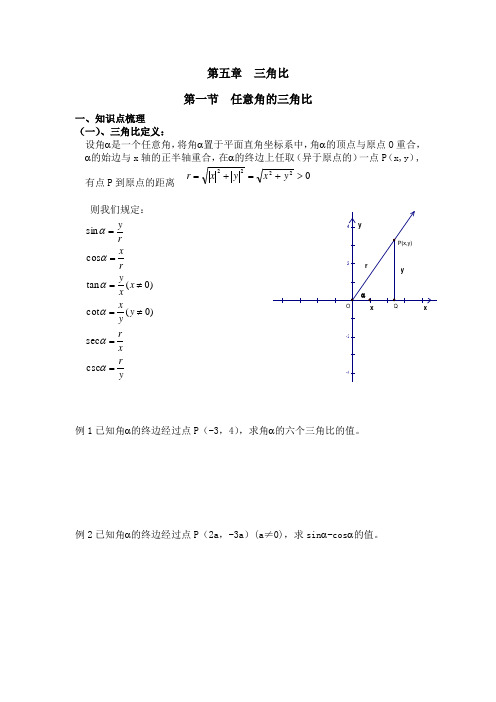
第五章 三角比 第一节 任意角的三角比一、知识点梳理 （一）、三角比定义： 设角α是一个任意角，将角α置于平面直角坐标系中，角α的顶点与原点O 重合，α的始边与x 轴的正半轴重合，在α的终边上任取（异于原点的）一点P （x,y ）, 有点P 到原点的距离 02222>+=+=y x y x r则我们规定：y rx ry y xx x yr xr y ==≠=≠===ααααααcsc sec )0(cot )0(tan cos sin例1已知角α的终边经过点P （-3，4），求角α的六个三角比的值。

例2已知角α的终边经过点P （2a ，-3a ）(a ≠0)，求sin α-cos α的值。

例3求65π的六个三角比的值。

例4应用三角比的定义证明： （1）平方关系222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= （2）倒数关系sin αcsc α=1,cos αsec α=1,tan αcot α=1, （3）商数关系sin cos tan ,cot cos sin αααααα==专题训练1、分别求0、2π、π、23π、π的三角比值。

2、分别求6π、4π、3π、65π、43π、32π的三角比值。

3、已知角α的终边与函数y=-3x 的图形重合，求角α的各三角比的值。

4、已知角α的终边与x轴重合，求cosα得值。

评注：三角比的定义是三角知识的源头，务必充分理解，灵活应用，熟练掌握。

（二）、三角函数线：1、正弦线：无论α是第几象限角，过α的终边与单位圆的交点P作x轴的垂线，交x轴于M，有向线段MP的符号与点P的纵坐标y的符号一致，长度等于｜y｜．所以有→MP=y=sinα．我们把有向线段→MP叫做角α的正弦线，正弦线是角α的正弦值的几何形式．2、余弦线：有向线段→OM叫做α的余弦线。

3、正切线：过A（1，0）点作单位圆的切线（x轴的垂线），设α的终边或其反向延长线与这条切线交于T点，那么有向线段→AT叫做角α的正切线。

5.2.1 三角函数的概念本节课选自《普通高中课程标准数学教科书-必修第一册》（人教A版）第五章《三角函数》,本节课是第3课时,这是节关于任意角的三角函数的概念课.三角函数是高中范围内继指数函数、对数函数和幂函数之后学习的函数,是函数的一个下位概念,与指对数函数、幂函数属于同一抽象( 概括)层次。

它是一种重要的基本初等函数,是解决实际问题的重要工具,也是学习数学中其他知识内容的基础。

在初中,学生已学过锐角三角函数,知道直角三角形中锐角三角函数等于相应边长的比值。

在此基础上,随着角的概念的推广,引入弧度制,相应地将锐角三角函数推广为任意角的三角函数,此时它与三角形已经没有什么关系了。

任意角的三角函数是研究一个实数集( 角的弧度数构成的集合)到另一个实数集( 角的终边与单位圆交点的坐标或其比值构成的集合)的对应关系。

认识它需要借助单位圆、角的终边以及两者的交点这些几何图形的直观帮助,这里体现了数形结合的思想,由锐角三角函数到坐标表示的锐角三角函数,再到单位圆上的点的坐标表示的锐角三角函数,直至得到任意角的三角函数的定义,体现了合情推理的思想方法。

本节课将围绕任意角三角函数的概念展开,任意角三角函数的概念是本节课的重点,能够利用单位圆认识这个概念是解决教学重点的关键。

A.借助单位圆理解任意角三角函数的定义;B.根据定义认识函数值的符号,理解诱导公式一;C.能初步运用定义分析和解决与三角函数值有关的一些简单问题;D.体验三角函数概念的产生、发展过程,领悟直角坐标系的工具功能,丰富数形结1.教学重点:任意角的三角函数（正弦函数、余弦函数、正切函数）的定义;2.教学难点:任意角的三角函数概念的建构过程。

多媒体一、复习回顾,温故知新 1. 1弧度角的定义【答案】等于半径长的圆弧所对的圆心角 2. 角度制与弧度制的换算:【答案】︒︒︒≈==30.571801180）（弧度，ππ3. 关于扇形的公式【答案】.21)3(;21)2(;12lR S R S R l ===αα）（ 4.在初中我们是如何定义锐角三角函数的? 【答案】.tan ,cos ,sin abc a c b ===ααα二、探索新知探究一.角α的始边在x 轴非负半轴,终边与单位圆交于点P 。

5．2 任意角的三角函数5.2.1任意角三角函数的定义第1课时用比值定义三角函数教材要点要点一任意角的三角函数的定义如图，设α是一个任意角，在角α的终边OM上任取不同于原点O的点P，利用点P的坐标(x，y)的定义：sinα＝________，cosα＝________，tanα＝________，其中r＝√x2+y2.以上三个比值分别称为角α的正弦、余弦、正切，y＝sinα，y＝cosα，y＝tanα分别叫作角α的正弦函数、余弦函数、正切函数，以上三种函数都称为三角函数．状元随笔角α的三角函数值是比值，是一个实数，这个实数的大小与点P(x，y)在终边上的位置无关．要点二三角函数的定义域正弦函数y＝sinα，定义域为________；余弦函数y ＝cos α，定义域为________； 正切函数y ＝tan α，定义域为________．基础自测1.思考辨析(正确的画“√”，错误的画“×”) (1)sin α表示sin 与α的乘积．( )(2)角的三角函数值随终边上点的位置变化而变化．( )(3)设角α终边上的点P (x ，y )，r ＝|OP |≠0，则sin α＝yr ，且y 越大，sin α的值越大．( )(4)终边落在y 轴上的角的正切函数值为0.( ) 2．已知角α的终边与单位圆交于点(−√32，−12)，则sin α的值为( )A ．－√32B ．－12C ．√32D ．12 3．若角θ的终边经过点P (−√22，√22)，则tan θ＝( )A ．√22B ．－√22C ．－1D ．－√324．如果角α的终边经过点P (－1，√3)，则cos α＝________．题型1 单位圆法求三角函数值例1 (1)角α终边与单位圆相交于点M (√32，12)，则cos α＋sin α的值为________． (2)利用定义求5π6的正弦、余弦和正切值．方法归纳1．若已知角α的大小，只需确定出角α的终边与以坐标原点为圆心的单位圆的交点坐标，即可求出角α的各三角函数值．2．若已知角α终边上一点P (x ，y )(x ≠0)是以坐标原点为圆心的单位圆上的点，则sinα＝y ，cos α＝x ，tan α＝yx .跟踪训练1 (1)在平面直角坐标系中，以x 轴的非负半轴为角的始边，如果角α，β的终边分别与单位圆交于点(1213，513)和(−35，45)，那么sin αcos β＝( )A ．－3665B ．－313C ．413D ．4865(2)在平面直角坐标系中，角α的终边与单位圆交于点A ，点A 的纵坐标为35，求tan α.题型2 坐标法求三角函数值例2 已知角α的终边过点P (－3a ，4a )(a ≠0)，求2sin α＋cos α的值．方法归纳(1)已知角α终边上任意一点的坐标求三角函数值的方法，cosα在α的终边上任选一点P(x，y)，设P到原点的距离为r(r＞0)，则sinα＝yr .当已知α的终边上一点求α的三角函数值时，用该方法更方便．＝xr(2)当角α的终边上点的坐标以参数形式给出时，要根据问题的实际情况对参数进行分类讨论．，则m＝( ) 跟踪训练2 已知角α的终边上一点P(1，m)，且sinα＝√63A．±√2B．√2C．－√2D．√62题型3 三角函数概念的综合应用的值．例3 已知角α的终边在直线y＝－3x上，求10sinα＋3cosα方法归纳在解决有关角的终边在直线上的问题时，应注意到角的终边为射线，所以应分两种情况进行处理，取射线上异于原点的任意一点的坐标(a，b)，则对应角的三角函数值分别为sinα＝√a 2+b 2，cos α＝√a 2+b 2，tan α＝ba .跟踪训练3 已知角α的终边在直线y ＝√3x 上，求sin α，cos α，tan α的值．易错辨析 忽略题目中的隐含条件致误例4 已知角α的终边过点P (－8m ，－6sin30°)且cos α＝－45，则m 的值为( )A ．12B ．－12C ．－√32D ．±12解析：∵点P 到原点的距离r ＝√64m 2+9， ∴cos α＝√64m 2+9＝－45，即4m 264m 2+9＝125，且m ＞0，解得m ＝12. 故选A. 答案：A 易错警示课堂十分钟1．已知角α的顶点在原点，始边与x 轴的非负半轴重合，终边过点(−35，45)，则tanα的值为( )A ．－43B ．－34 C ．－45D ．－352．在平面直角坐标系中，角θ的顶点与原点重合，角θ的始边与x 轴非负半轴重合，角θ的终边经过点P (－3，4)，则cos θ＝( )A ．－35B ．45C ．－325D ．4253．若角α的终边过点(2sin30°，－2cos30°)，则sin α的值等于( ) A ．12B ．－12C ．－√32D ．－√334．已知角α的终边在射线y ＝－x (x ≤0)上，则cos α＝________． 5．已知角θ的终边上一点P (－√3，m )，且sin θ＝√24m .求cos θ与tan θ.5．2 任意角的三角函数 5．2.1 任意角三角函数的定义第1课时 用比值定义三角函数新知初探·课前预习要点一y rx ryx要点二R R {α|α≠π2+kπ，k ∈Z}[基础自测]1．答案：(1)× (2)× (3)× (4)×2．解析：根据任意角的正弦定义，可得sin α＝y ＝－12. 故选B. 答案：B3．解析：角θ的终边经过点P (－√22，√22)，则tan θ＝√22－√22＝－1，故选C. 答案：C4．解析：∵角α的终边经过点P (－1，√3)，∴|OP |＝√（−1）2+（√3）2＝2，∴cos α＝－12.答案：－12题型探究·课堂解透例1 解析：(1)由三角函数的定义得sin α＝12，cos α＝32，所以cos α＋sin α＝32＋12＝3＋12.(2)如图所示，5π6的终边与单位圆的交点为P ，过P 作PB ⊥x 轴于点B ，在△OPB 中，|OP |＝1，∠POB ＝π6，则|PB |＝12，|OB |＝32，则P ⎝ ⎛⎭⎪⎫－32，12 所以sin 5π6＝12，cos 5π6＝－32tan 5π6＝－33.答案：(1)3＋12(2)见解析 跟踪训练1 解析：(1)由三角函数的定义sin α＝513，cos β＝－35，所以sin αcos β＝513×⎝ ⎛⎭⎪⎫－35＝－313.故选B.(2)由题意，设点A 的坐标为⎝ ⎛⎭⎪⎫x ，35，所以x 2＋⎝ ⎛⎭⎪⎫352＝1，解得x ＝45或－45. 当x ＝45时，tan α＝3545＝34；当x ＝－45时，tan α＝35－45＝－34.答案：(1)B (2)见解析例2 解析：r ＝（－3a ）2＋（4a ）2＝5|a |， ①若a >0，则r ＝5a ，角α在第二象限．sin α＝y r ＝4a 5a ＝45，cos α＝x r ＝－3a 5a ＝－35，所以2sin α＋cos α＝85－35＝1.②若a <0，则r ＝－5a ，角α在第四象限， sin α＝4a －5a ＝－45，cos α＝－3a －5a ＝35.所以2sin α＋cos α＝－85＋35＝－1.综上所述：当a >0时，2sin α＋cos α＝1；当a <0时，2sin α＋cos α＝－1. 跟踪训练2 解析：角α的终边上一点P (1，m )， 所以r ＝|OP |＝1＋m 2， 所以sin α＝m1＋m2＝63>0， 解得m ＝ 2. 故选B. 答案：B例3 解析：由题意知，cos α≠0.设角α的终边上任意一点为P (k ，－3k )(k ≠0)， 则x ＝k ，y ＝－3k ，r ＝k 2＋（－3k ）2＝10|k |. (1)当k >0时，r ＝10k ，α是第四象限角， sin α＝y r＝－3k10k＝－31010，1cos α＝r x ＝10kk＝10， 所以10sin α＋3cos α＝10×⎝ ⎛⎭⎪⎫－31010＋310＝－310＋310＝0.(2)当k <0时，r ＝－10k ，α是第二象限角，sin α＝y r ＝－3k －10k ＝31010，1cos α＝r x ＝－10kk＝－10， 所以10sin α＋3cos α＝10×31010＋3×(－10)＝310－310＝0.综上所述，10sin α＋3cos α＝0.跟踪训练3 解析：因为角α的终边在直线y ＝3x 上，所以可设P (a ，3a )(a ≠0)为角α终边上任意一点，则r ＝a 2＋（3a ）2＝2|a |(a ≠0).若a >0，则α为第一象限角，r ＝2a ， 所以sin α＝3a 2a ＝32，cos α＝a 2a ＝12， tan α＝3aa＝ 3.若a <0时，则α为第三象限角，r ＝－2a ， 所以sin α＝3a －2a ＝－32，cos α＝a －2a ＝－12，tan α＝3aa＝ 3.[课堂十分钟]1．解析：由正切函数的定义可得，tan α＝45−35＝－43.故选A. 答案：A2．解析：∵角θ的顶点与原点重合，角θ的始边与x 轴非负半轴重合， 角θ的终边经过点P (－3，4)，则cos θ＝√9+16＝－35， 故选A. 答案：A3．解析：∵x ＝2sin 30°＝1，y ＝－2cos 30°＝－√3，∴r ＝√12+(−√3)2＝2，∴sin α＝y r＝－√32.故选C. 答案：C4．解析：在角α的终边y ＝－x (x ≤0)上任取一点(－1，1)， 则cos α＝√1+1＝－√22.答案：－225．解析：由题意得sin θ＝mm2＋3＝24m，若m＝0，则cosθ＝－1，tan θ＝0. 若m≠0，则m＝± 5.当m＝5时，cosθ＝－64，tan θ＝－153；当m＝－5时，cosθ＝－64，tan θ＝153.11。

第五章 三角比知识结构5.1 任意角及其度量考点诠释1.任意角 平面内由一条射线绕着它的端点从初始位置（始边）旋转到终止位置（终边）所形成的图形．（1）正角 一条射线绕端点按逆时针方向旋转所形成的角为正角； （2）负角 一条射线绕端点按顺时针方向旋转所形成的角为负角； （3）零角 一条射线没有旋转时形成的角为零角．2.象限角 在平面直角坐标系内，将角的顶点与坐标原点重合，角的始边与x 轴的正半轴重合，角的终边在第几象限，就称这个角是第几象限的角．当角的终边在坐标轴上时，这个角不属于任何象限． 3.终边相同的角与角α终边相同的角表示为{}360,k k Z ββα=⋅+∈．4.弧度制的概念将长度等于半径的圆弧所对圆心角的大小叫做1弧度的角，记为1rad ，通常省略单位rad ，用弧度来度量角的大小是角的另一种度量制度——弧度制． 5.角度与弧度的互换弧度制与角度制之间存在着下列换算关系：1180π︒=弧度，1弧度=180()57.3π︒︒≈6.弧长公式、扇形的面积公式 弧长公式 l r α=⋅； 扇形面积公式 21122S l r r α=⋅=⋅ 7. 一个角确定了，它的终边也就唯一确定了；但反过来，若角的终边确定了，则它表示的角并不确定，这样的角有无数个，它们之间大小相差2π的整数倍．即与角α终边相同的角的集合表示为{|2,}x x k k Z πα=+∈（或{|360,}x x k k Z α=⋅+∈）．要注意：在同一个表达式中弧度与角度不能混用． 8.弧度制下象限角的范围 第一象限角的范围 22,2k k k Z πππ⎛⎫+∈ ⎪⎝⎭，； 第二象限角的范围 22,2k k k Z ππππ⎛⎫++∈ ⎪⎝⎭，； 第三象限角的范围 322,2k k k Z ππππ⎛⎫++∈ ⎪⎝⎭，； 第四象限角的范围 3222,2k k k Z ππππ⎛⎫++∈ ⎪⎝⎭，或22,2k k k Z πππ⎛⎫-∈ ⎪⎝⎭，. 9.终边在各坐标轴上的角的表示角α终边在x 轴正方向 2k k Z π∈（）； 角α终边在x 轴负方向 2k k Z ππ+∈（）；角α终边在y 轴正方向 22k k Z ππ+∈（）；角α终边在y 轴负方向 322k k Z ππ+∈（）或22k k Z ππ-∈（） 例题精析例1 设角123460,46,75,208x x x x =0=-0==-. （1）指出它们所在的象限. （2）在72036-0范围内找出与它们终边相同的角.（3）将它们用弧度制表示出来，并写出与它们终边相同的角的集合. 思维引领怎样用不等式或集合表示象限角以及用集合来表示终边相同的角.精辟分析（1）12,x x 在第三象限，3x 在第一象限，4x 在第二象限. （2）与1x 终边相同的角为600360,k k Z β=+⋅∈. 由72036β-≤<0，得240,120,480β=--. 所以在72036-0范围内与1x 终边相同的角有480,120,240--.同理可得： 在72036-0范围内与2x 终边相同的角有100,260-. 在72036-0范围内与3x 终边相同的角有285,645--. 在72036-0范围内与4x 终边相同的角有568,152-.（3）160x π10=0=3. 与1x 终边相同的角的集合为1{|600360,}S k k Z ββ==+⋅∈.26x π23=-40=-9. 与2x 终边相同的角的集合为2{|460360,}S k k Z ββ==-+⋅∈.x π35=75=12. 与3x 终边相同的角的集合为3{|75360,}S k k Z ββ==+⋅∈4x π52=-208=45. 与4x 终边相同的角的集合为4{|208360,}S k k Z ββ==-+⋅∈.方法规律总结（1）要确定角x 所在的象限，可以先将角写成360()x x k k Z ︒=+⋅∈ （0360x ︒︒︒≤<）的形式，再由角x ︒所在的象限来判断角x 所在的象限.（2）利用终边相同的角的集合可以求适合某些条件的角，方法是先写出与这个角的终边相同的所有角的集合，然后通过对集合中的参数k 赋值来求得所需角. （3）180π︒=注意角度与弧度不能在同一个表达式中出现.误区警示要搞清“终边相同的角”、“象限角”等概念的联系与区别．例2（1）如果角α是第三象限角，那么角,2αα-的终边落在何处？（2）写出终边在直线y =上的角的集合；（3）若角θ的终边与135角的终边相同，求在[0,360)内终边与3θ角的终边相同的角. 思维引领写出满足条件的角α完整的不等式形式，解关于,2αα-的不等式，根据所得的不等式从代数和几何意义两个角度去理解终边所在的位置.精辟分析（1）由角α是第三象限角得3222k k πππαπ+<<+ 所以3222k k ππαππ--<-<-- 即22()2k k k Z ππαππ+<-<+∈所以α-的终边在第二象限； 由3222k k πππαπ+<<+得24234()k k k Z ππαππ+<<+∈ ∴角2α的终边在第一、二象限及y 轴的非负半轴.（2）在(0,)π内终边在直线y =上的角是3π，∴终边在直线y =上的角的集合为{|,}3k k Z πααπ=+∈.（3）324k θππ=+ 12()343k k Z θππ∴=+∈ 由题意120243k πππ≤+<得321,88k k Z -≤<∈. 0,1,2k ∴=即在在[0,)π2内终边与3θ角的终边相同的角为1119,,41212πππ.方法规律总结（1）写出满足条件的角α完整的不等式形式，解关于,2αα-的不等式，根据所得的不等式从代数和几何意义两个角度去理解终边所在的位置.（2）先找出满足条件（y =）的最小正角，然后再写出最简结论.（3）利用终边相同的角的集合可以求适合某些条件的角，方法是先写出与这个角的终边相同的所有角的集合，然后通过对集合中的参数k 赋值来求得所需角.误区警示满足条件的角α不等式形式一定要完整，否则就可以出现漏解的情况.再者不要忽略坐标轴上的角.例3 （1）已知弧长为10cm 的弧所对的圆心角为120,求这条弧所在圆的半径. （2）已知一扇形的圆心角为60，半径为4cm ，求此扇形的弧长和面积.思维引领（1）弧度制下弧长、扇形的面积公式简单明了：l r α=,21122S lr r α==. （2）灵活运用公式列出方程组是解答这类问题的关键.精辟分析（1） 设这条弧所在的圆的半径为r ，则l r α=.2101533lr απαππ=∴=== （2）设扇形的弧长、面积分别为,l S ，则244()3311484()2233l r cm S lr cm παπππ==⨯===⨯⨯=方法规律总结先将角度转化为弧度，再使用弧长公式和扇形的面积公式.误区警示弧长和扇形的面积公式要在弧度制下才简单明了,要先将角用弧度来表示.拓展训练一、填空题1．角α的终边落在区间5(3,)2--ππ内，则角α是第 象限的角．2．终边落在第一、三象限的角平分线上的角的集合是 ，第一象限的角平分线上的角的集合为 ．3．若α是第三象限角，则2α是第 象限的角． 4．一个半径为2的扇形，若它的周长等于所在圆的周长，则该扇形的圆心角是．5．已知扇形OAB 的面积是10cm ,它的周长是cm,则中心角AOB ∠的弧度数为_____________________.6．若{|22,},{|66}33A x k x k k ZB x x ππππ=-<<+∈=-≤≤,则________________A B =.二、选择题7．下列命题中，正确的是 （ ） （A ）终边在第一象限的角是锐角 （B ）终边在第二象限的角是钝角 （C ）相等的角终边相同 （D ）终边相同的角是相等的角 8．若α是第一象限的角，则-πα是 （ ）(A)第一象限的角 (B) 第二象限的角 (C) 第三象限的角 (D) 第四象限的角 三、解答题9．若α是钝角，且α与9α的终边相同，求角α的弧度数．10． 已知扇形的周长为20cm ，问扇形的圆心角α为何值时扇形的面积S 最大，并求出S 的最大值．11．在扇形AOB 中，90AOB ∠=,弧AB 的长为l ,求此扇形内切圆的面积. 12.已知集合,,,266k M k Z P k k Z πππααββπ⎧⎫⎧⎫==+∈==±∈⎨⎬⎨⎬⎩⎭⎩⎭，求,MP M P ．5.2 任意角的三角比考点诠释1.任意角的三角比的定义 如图所示， 在任意角α终边上任取一点(,)P x y （P 与原点不重合），|OP |0==>r ，则有sin cos ==yrxrααtan (,)2=≠+∈y k k Z x πααπ cot (,)xk k Z yααπ=≠∈sec (,)2=≠+∈r k k Z x πααπ csc (,)rk k Z yα=α≠π∈ 2．角α各三角比在每个象限的符号：3．终边相同的角的同名三角比相等（第一组诱导公式）：s i n (2)s i n k παα+=；cos(2)cos k παα+=；tan(2)tan k παα+=； c o t (2)c o t k παα+=，其中k Z ∈． 4.三角函数线：设角α的终边与原点为圆心的单位圆交于点P ，则有向线段,,MP OM AT 的数量分别等于角α的正弦、余弦、正切的值，有向线段,,MP OM AT 分别称为角α的正弦线、余弦线和正切线．例题精析例1已知角α的终边经过点(12,5)-P t t （0≠t ），求角α的六个三角比．思维引领任意角的六个三角比的定义，可以利用其终边上任意一点的坐标(,)x y 与该点到原点的距离r 在定义，若角的终边上的点含参数，要对参数进行讨论.精辟分析解 因为角α的终边经过(12,5)-P t t ，所以12,5==-x t y t.13013130.t t r t t t >⎧====⎨-<⎩ , 当0>t 时12,5==-x t y t ，13=r t .55sin 1313-===-y t x r t ；1212cos 1313===x t r t α；55tan 1212-===-y t x t α； 1212c o t 55===--x t y a α；1313sec 1212===r t x t α；1313csc 55===--r t y t α．当0<t 时12,5==-x t y t ，13=-r t . 55sin 1313-===-y t x r t ；1212cos 1313===--x t r t α；55tan 1212-===-y t x t α； 1212c o t 55===--x t y a α；1313sec 1212-===-r t x t α；1313csc 55-===-r t y t α．方法规律总结（1）利用任意角的三角比的定义.（2）若角的终边上的点含参数，要对参数进行讨论.误区警示若角的终边上的点含参数，要对参数进行讨论. 例2 求下列各三角比： （1）23sin()6-π （2）31cos 4⎛⎫- ⎪⎝⎭π （3）tan(315)- 思维引领第一组诱导公式的应用，解题时可把已知角化为2(02)k πααπ+≤<或360(0360)k αα+≤<的形式． 精辟分析解（1）231sin()sin(22)sin 6662-=-⨯+==ππππ． （2）31cos cos(42)cos 4442⎛⎫-=-⨯+==⎪⎝⎭ππππ.（3）()()()tan 315tan 36045tan 136045tan 451-=-+=-⨯+==．方法规律总结本例先把已知角化为2(02)k πααπ+≤<或360(0360)k αα+≤<的形式，再利用终边相同的同名三角比相等解决问题．误区警示（1）记住一些特殊角的三角值. （2）三角比在各个象限内的符号. （3）三角比的诱导公式（一）.例3 根据下列条件确定θ所属象限（不考虑角的终边在坐标轴上）： （1）sin 0θ<且cos 0θ>; （2）cos tan 0θθ⋅<; （3）csc 0θ>且sec 0θ<; （4）sin 0cot θθ>. 思维引领确定角α各三角比在每个象限的符号以及正弦线、余弦线和正切线的应用.精辟分析解（1）sin 0θ<，∴θ是第三或第四象限的角；又cos 0,θθ>∴是第一或第四象限的角，所以θ是第四象限的角． （2）cos tan 0,θθ⋅<∴cos θ与tan θ异号．如果cos 0θ>且tan 0θ<，则θ是第四象限的角；如果cos 0θ<且tan 0θ>，则θ是第三象限的角．所以θ是第三或第四象限的角．（3）csc 0,θθ>∴是第一或第二象限的角；又sec 0,θθ<∴是第二或第三象限的角，所以θ是第二象限的角．（4）sin 0,sin cot θθθ>∴与cot θ同号．如果sin 0θ>且cot 0θ>，则θ是第一象限的角；如果sin 0θ<且cot 0θ<，则θ是第四象限的角．所以θ是第一或第四象限的角．方法规律总结已知同一个角的不同三角比的符号，要确定角所在的象限时，应分别根据各个三角比的符号确定角所在的象限，再求出其公共象限．需注意sin 0,θ>θ属第一、二象限且包括y 轴正向．误区警示要画出正确的三角函数线；因为不考虑角的终边在坐标轴上，所以只要找出满足条件的象限即可．拓展训练一、填空题1．求下列各三角比： 13tan4=π ； 5cot 6⎛⎫-= ⎪⎝⎭π ； 25csc 4π⎛⎫=⎪⎝⎭； 25sin 3⎛⎫-= ⎪⎝⎭π ；2．若角θ的终边有一点(,8)P a ，且3cos 5=-θ，则=a ． 3．设θ是第三象限的角，则sin tan θθ⋅的符号是 ，而sec sinθθ⋅的符号是 ．4．若α是第三象限角，且sinsin22αα=-，则角2α是第 象限角． 5．若α是第三象限角，则下列各式中①sec tan 0αα⋅>②cos csc 0αα⋅<③sin tan 0αα-<④cot sec 0αα+>．其中正确的是 ．6．已知sin sin ,cos cos =-=-θθθθ，且sin cos ≠0θθ，则(tan ,sin )P θθ在第 象限. 二、选择题7．在(0,2)π内，使sin cos >x x 成立的x 的取值范围是 （ ）（A ）5(,)(,)424ππππ （B ）(,)4ππ （C ）5(,)44ππ （D ）53(,)(,)4242ππππ8．sin 3cos3+的值 （ ）(A)大于0 (B)小于0 (C)大于等于0 (D)不确定 三、解答题9．已知角α的顶点在原点，始边为x 轴的非负半轴，若角α终边经过点()P y ，且sin (0)=≠y y α，判断角α所在的象限，并求cos α和tan α的值. 10．求分别适合下列条件的角α的集合：（1）sin α≥（2）1cos 2α≤-11．根据下列条件分别写出角θ所属象限（不考虑角的终边在坐标轴上）： （1）sin θ与cot θ异号； （2）cos θ与tan θ同号；（3）tan 0cot θθ> （4）sin 0cos 0θθ<⎧⎨>⎩12．设{}sin 0,,23A x x x R B x x ππ⎧⎫=≥∈=+<⎨⎬⎩⎭，求A B ． 五年高考试题1．（2010上海）“()24x k k Z ππ=+∈”是“tan 1x =”成立的 （ ）（A ）充分不必要条件. （B ）必要不充分条件.（C ）充分条件. （D ）既不充分也不必要条件.2．（2011江西）已知角θ的顶点为坐标原点，始边为x 轴的正半轴，若()4,p y 是角θ终边上一点，且sin θ=，则y=_______. 3．（2011全国Ⅰ）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ=（A ）45- （B ）35- （C ）35 （D ）454．（山东理）若点（a,9）在函数3xy =的图象上，则tan=6a π的值为（A ）0 (B)(C) 1 (D) 5．（2011全国Ⅱ）已知3(),tan 22παπα∈=，，则cos α= ．5.3 同角三角比的关系和诱导公式考点诠释1．同角三角比的关系 （1）倒数关系1csc sin =⋅αα；1sec cos =⋅αα；1cot tan =⋅αα；（2）商数关系αααcos sin tan =；ααsin cos cot =； （3）平方关系1cos sin 22=+αα；αα22sec 1tan =+；αα22csc 1cot =+．一般地，如果已知角α的一个三角比且已知它终边所在的象限，那么角α的其它三角比可以唯一确定，如果未给出角α所在的象限，则根据终边可能所在的象限需分别进行讨论，并相应地求出其它三角比．2．第二组诱导公式：ααsin )sin(-=-，ααcos )cos(=-，ααtan )tan(-=-，ααcot )cot(-=-．第三组诱导公式：ααπsin )sin(-=+，ααπcos )cos(-=+，ααπtan )tan(=+，ααπcot )cot(=+．第四组诱导公式：ααπsin )sin(=-，ααπcos )cos(-=-，ααπtan )tan(-=-，ααπcot )cot(-=-．第五组诱导公式：sin cos 2παα⎛⎫-=⎪⎝⎭； cos sin 2παα⎛⎫-= ⎪⎝⎭； tan cot 2παα⎛⎫-=⎪⎝⎭； cot tan 2παα⎛⎫-= ⎪⎝⎭． 第六组诱导公式：sin cos 2παα⎛⎫+=⎪⎝⎭； c o s s in 2παα⎛⎫+=- ⎪⎝⎭； tan cot 2παα⎛⎫+=-⎪⎝⎭； cot tan 2παα⎛⎫+=- ⎪⎝⎭． 虽然诱导公式共有六组，但本质上只要掌握两个特点，即三角比是否变化，符号如何确定．我们可以借助口诀“奇变偶不变，符号看象限”来帮助记忆．“奇变偶不变”的意思是：如果α前加的是2π的奇数倍，那么等号后面的三角比值名改变，如果α前加的是2π的偶数倍，那么等号后面的三角比值名不改变．“符号看象限”的意思是：等号后面三角比值的正负号是将α看成锐角时等号前面的角所在象限内原三角比的符号来确定．4. 利用诱导公式把任意角的三角比转化为锐角的三角比的步骤是任意角的三角比正角的三角比~2π锐角三角比例题精析例1（1）已知3cos 5α=-，且α为第二象限角，求sin ,tan αα的值. （2）已知3cos 5α=-，求sin ,tan αα的值. （3）已知cos m α=，求sin ,tan αα的值.思维引领同角三角比的关系以及各三角比在各个象限内的符号的判断.精辟分析（1）223cos ,sin cos 15ααα=-+=2216sin 1cos 25αα∴=-=又α为第二象限角，sin 0α∴>44sin ,tan 53αα∴==- （2）当α为第二象限角时，44sin ,tan 53αα==- 当α为第三象限角时，44sin ,tan 53αα=-=（3）当α在第一、二象限角时，sin tan mαα==；当α在第三、四象限角时，sin tan αα==；当α终边在x 轴上时，sin tan 0αα==； 当α终边在y 轴上时，sin 1α=±，tan α不存在.方法规律总结已知一个角的某个三角比值，可以利用同角三角比的关系式求出其他的三角比值，一定要注意各个三角比值在各个象限内的符号.误区警示（1）公式22sin cos 1αα+=对任意的R α∈都成立，公式αααcos sin tan =仅在,2k k Z παπ≠+∈时成立.（2）应用公式的变形sin α=“±”由角α所在的象限确定）等时，注意讨论角α的终边所在的位置.（3）不能忽略角α的终边落在坐标轴上时的各个三角比值. 例2 化简（1）[][])()2cos()2sin()12(sin )12(sin Z n n n n n ∈+-⋅---+++παπαπαπα.（2）[]sin()cos()()cos (1)n n n Z n π-α-π-α∈+π+α.（3）11sin(2)cos()cos()cos()229cos()sin(3)sin(-)sin()2ππβπββπβπβπβπβπβ-++----+.思维引领六组诱导公式的直接应用.精辟分析（1）解 原式[][])cos(sin )(2sin )(2sin αααππαππ-⋅++-+++=n nαααααααπαπsec 2cos sin sin 2cos sin )sin()sin(-=⋅-=⋅+++=．（2）解 ①当n 是奇数，即Z k k n ∈+=,12时， 原式()[][]()[]απαπαπ++-+-⋅-+=22cos )12(cos 12sin k k k [][]()[]απαππαππ+++--⋅-+=12cos )(2cos )(2sin k k k[]ααααααπαπsin cos )cos (sin cos )(cos )sin(-=-⋅=+-⋅-=；②当n 是偶数，即Z k k n ∈=,2时， 原式()[][])cos(cos sin )(2cos )cos()sin(12cos )2cos()2sin(απαααππαααπαπαπ+⋅-=++--=++--⋅-=k k k kααααsin cos cos sin =-⋅-=．（3）原式sin (cos )(sin )(sin )tan cos sin sin cos βββββββββ----==--.方法规律总结运用诱导公式求解问题时要注意两点：一是要熟记公式；二要灵活合理的运用公式.误区警示在使用各组诱导公式时，一定要注意各组三角比值的符号． 例3 已知tan =3α，求下列各式的值： （1）ααααcos sin 3sin 4cos -+的值；（2）αααα22cos 2sin cos sin +⋅+的值．思维引领（1）sin tan cos ααα=，代入即可. （2）将多项式转化为齐次多项式，化弦为切.精辟分析（1）cos 4sin 14tan 133sin cos 3tan 18αααααα++==--；（2）αααα22cos 2sin cos sin +⋅+222222sin cos sin 2cos 1sin cos sin 2cos sin cos αααααααααα+⋅+=+⋅+=+22tan tan 2tan 1ααα++=+75= 方法规律总结（1）学会灵活运用同角关系式22sin cos 1αα+=以及变形公式2211t a n ,s i n t a n c o s c o sααααα+==等.（2）求形如sin cos sin cos a b c d αααα++齐次多项式的值时，可将tan k α=化为sin cos k αα=代入求解（化弦为切）或将分子分母同时除以cos α，再求解，但是要注意cos 0α≠. 求形如22sin cos sin cos a b c αααα+⋅+的齐次多项式的值时，可化整式为分式（分母除以1，221sin cos αα=+，再除以2cos α，化为关于tan α的表达式，然后求值）.误区警示若使用列出方程22sin tan cos sin cos 1ααααα⎧=⎪⎨⎪+=⎩求解的方法，开方时要对角α的终边所在的位置分类讨论.例4 求证：cos (2sec tan )(sec 2tan )2cos 3tan +-=-ααααααα思维引领证明三角恒等式的过程，实际上是“化异为同”的过程，即化去形式上的异，而呈现实质上的同，在证明三角恒等式时，往往是从较复杂处向形式较简单处推演．精辟分析证明 左边=2sin 12sin cos ()()cos cos cos cos +-ααααααα211(2sin )(12sin )(22sin 3sin )cos cos =+-=--αααααα21(2cos 3sin )2cos 3tan cos =-=-=ααααα右边． 所以等式成立．方法规律总结一般采用的方法是“切割化弦”.误区警示注意同角的各个三角比值之间的相互转化关系.例5 已知1sin cos 05+=-<<αααπ，且， 求tan α的值．思维引领运用1cos sin 22=+αα把正余弦的和差积联系起来，是三角比化简求值中常用的方法．精辟分析解 对1sin cos 5+=-αα （1）两边平方得112sin cos 25+=αα，即12sin cos 25=-αα， 249(sin cos ),0,sin cos 0sin cos 0252π∴α-α=<α<παα<∴<α<π∴α-α>， 因此7sin cos 5-=αα. (2) 由（1）、（2）联立的方程组得3sin 5=α，4cos 5=-α，所以3tan 4=-α.方法规律总结已知sin cos a b c αα+=求sin ,cos αα的问题可通过建立方程组求解，也可以将等式两边平方，再利用一元二次方程求根的方法求解，答案是一组还是两组由方程本身以及角的范围决定.误区警示（1）平方关系使sin cos αα±与sin cos αα之间的转化更加灵活，求最值时要注意等号是否成立.（2）领会方程的思想，以及变量代换、函数的思想.拓展训练一、填空题1．4222sin sin cos cos a a a a ++= ． 2．（1）已知21sin -=α，且(0,2)∈απ，则角α= ； （2）已知23)cos(=+απ，且(,)∈-αππ，则角α= ； 3．已知3)cot(-=-απ，且0)cos(<-α，则=-+-)tan()2sin(ααπ ； 4．已知5sin cos 3ββ+=，则sin cos ββ= ．5．若5cos 3sin 76sin 2cos a aa a+=-，则tan a = ．6．若a+的值为 ．7．已知1sin cos 2+=αα，则tan cot +=αα ． 二、选择题 8．化简)3tan()cos()cot()tan()2sin(απαππααπαπ----+- （ ）（A ）1 （B ）1- （C ）αsin （D ）αtan -9．已知tan cot 2a -=α，则33tan cot a a -的值为 （ ）(A) 6 (B) 6- (C) 8 (D) 14 三、解答题 10．求值:：（1）30csc 180sec 0cos 270csc 45tan ⋅-+⋅； （2）ππππππ47cos 411sin 35cos 67sin 6cos3sin⋅+⋅+-； （3）⎪⎭⎫ ⎝⎛-⋅⎪⎭⎫ ⎝⎛-⋅⎪⎭⎫⎝⎛-⋅⎪⎭⎫ ⎝⎛-πππππ611sin 34tan 311cos 67cos 65tan11．求证：αααααα2cos cot tan 11tan cos sin 21-+=--12．已知224sin 6sin cos 3cos 0,(0,)2x x x x x π--+=∈，求（1）cos x . （2）5sin 3cos cos sin x xx x-+.（3）225sin 3cos sin cos x x x x ++. （2）5sin 3cos 5tan 31cos sin 1tan 3x x x x x x --==-++13．已知sin ,cos αα是方程2220x ax b ++=的两个根，且02,,a b απ≤<为整数，求角α.14．是否存在一个实数k ,使方程286210x kx k +++=的两个根是一个直角三角形的两个锐角的正弦？五年高考试题1．（2012山东）若42ππθ⎡⎤∈⎢⎥⎣⎦，,sin 2θ,则sin θ=（ ）A ．35B ．45C D ．342．（2012辽宁已知sin cos αα-=,α∈(0,π),则tan α=（ ）A ．-1B ．2-C ．2D ．13．（2012江西）若tan θ+1tan θ =4,则sin2θ= （ ）A ．15B ．14C ．13D ．124．（2011北京）在ABC 中，若5b =，4B π∠=，tan 2A =，则s i n A =_______，a =______.5．（2011全国理）若sin a = -45，a 是第一象限的角，则sin()4a π+=（A ） （B （C ） （D6．（全国Ⅱ理）已知(,)2παπ∈ ，sin α=5,则tan2α =___________.5.4 两角和与差的正弦、余弦和正切公式考点诠释1．两角和与差的正弦、余弦和正切公式cos()cos cos sin sin αβαβαβ+=-cos()cos cos sin sin αβαβαβ-=+ sin()sin cos cos sin αβαβαβ+=+ sin()sin cos cos sin αβαβαβ-=-tan tan tan()1tan tan αβαβαβ++=-tan tan tan()1tan tan αβαβαβ--=+变形形式：tan tan tan()(1tan tan )tan tan tan()(1tan tan )αβαβαβαβαβαβ+=+--=-+2．二倍角公式 （1）二倍角公式sin 22sin cos a a a= ;2222cos 2cos sin 2cos 112sin ααααα=-=-=- 22tan tan 21tan ααα=- （2）二倍角公式的变形形式 升幂公式：21sin (sin cos )22ααα±=± 221cos 2cos,1cos 2sin 22αααα+=-=降幂公式：221cos 21cos 2sin ,cos 22αααα-+== 3．辅助角公式sin cos )a b αααβ+=+，其中β（通常取02βπ≤<）由cos β=，sin β=确定．4．角的合理凑配及其应用 角的变换与凑配常见的有：2()()()()ααβαβαββα=++-=+--()()22αβαβααββαββ+-=+-=-+=+()()4466ππππααα=+-=+-例题精析例1 已知()()3123,cos ,sin 24135ππβααβαβ<<<-=+=-，求sin 2,cos 2αα的值.思维引领注意2()()ααβαβ=-++，直接使用两角和与差的正弦、余弦公式求解角的三角比值.精辟分析由324ππβα<<<可得3,240πππαβαβ<+<<-<. 45cos(),sin()513αβαβ∴+=--=sin sin[()()]2ααβαβ∴=++-sin()cos()cos()sin()αβαβαβαβ=+-++-312455651351365⎛⎫⎛⎫=-⋅+-⋅=- ⎪ ⎪⎝⎭⎝⎭cos cos[()()]2ααβαβ=++-cos()cos()sin()sin()αβαβαβαβ=+--+-412353351351365⎛⎫⎛⎫=-⋅--⋅=- ⎪ ⎪⎝⎭⎝⎭方法规律总结运用正弦、余弦两角和的公式解答本题的关键在于分析角的特点.例2 化简[2sin50sin10(1)]︒︒︒+思维引领“化切为弦”，运用两角和与差的三角比关系进行化简.误区警示化简的结果是使三角比化为最简的形式，即项数尽量少，名称尽量少，次数尽量低，能求值的尽量求出值来.精辟分析解原式[2sin50sin10(1︒︒=++⋅cos10[2sin 50sin10()]cos10︒︒︒︒︒+=+1cos1022[2sin 502sin10()]cos10︒︒︒︒︒+=+cos50(2sin 502sin10)cos10cos10︒︒︒︒︒=+⋅ 2(sin50cos10sin10cos50)︒︒︒︒=+2sin 60︒==方法规律总结本题在“化切为弦”的基础上，再运用辅助角公式惊醒转化.误区警示注意要对角αβ+与αβ-的范围进行讨论，为了避免在已知正（余）弦值求余（正）弦值时出现多余解的情况.例3 求值（1）tan 20tan 403tan 20tan 40++ （2）已知,αβ都是锐角，且sin αβ==，求αβ+. 思维引领在掌握两角和与差的正弦、余弦、正切公式的基础上，根据公式的结构特点，正向、逆向和变形使用公式.精辟分析（1）原式tan60(1tan 20tan 40)3tan 20tan 40︒=-+=（2）cos()cos cos sin sin 1αβαβαβ+=-=(,)0αβπ+∈4παβ∴+=方法规律总结在掌握两角和与差的正弦、余弦、正切公式的基础上，深刻理解公式的结构特点，既要善于正向运用公式，又要善于逆向运用公式和对公式变形.误区警示求角时要先求这个角的正弦、余弦和正切，再判断角的范围以确定用哪个公式，避免出现多余的解.拓展训练一、填空题1．在ABC ∆中，若54sin =A ，135cos -=B ，则C sin = ． 2．tan 75tan151tan 75tan15-+= .3．已知3cos 5=-θ，且32πθπ<<，则cos 4πθ⎛⎫-= ⎪⎝⎭ . 4．设11sin sin ,cos cos 22αβαβ-=--=，则cos()αβ-= . 5．cot 20cos103sin10tan702cos40______+-=. 6．若2sin =x x m ，则实数m 的范围是 .7.已知11sin sin ,cos cos 23αβαβ-=+=，则cos()αβ+=___________. 8. 化简42212cos 2cos 22tan()sin ()44x x x x ππ-+-+ . 9. 已知12cos 413πα⎛⎫-= ⎪⎝⎭，且344παπ<<，则cos α=____________．二、选择题10．如果θ角是第二象限的角，且满足cossin22θθ-=2θ是（ ） (A)第一象限的角 (B)第二象限的角 (C)第一或第三象限的角 (D)第三象限的角 11．已知,0,2παβ⎛⎫∈ ⎪⎝⎭且sin β==αβ+的值为 （ ） （A ）34π （B ）4π （C ）34π或4π （D ）32()4k k Z ππ+∈三、解答题12．已知tan ,tan αβ是方程2330x x --=的两根，求sin()cos()βααβ+-的值.13．已知(sin ,2)a θ=-与(1,cos )b θ=互相垂直，其中(0,)2πθ∈.（1）求sin θ和cos θ的值.（2）若5cos(),02πθϕϕϕ-=<<，求cos ϕ的值.14.若sin sin 2αβ+=，求cos cos αβ+的取值范围.15．已知46sin 4m mαα-=-，求m 的取值范围．五年高考试题1．（2012重庆）设tan ,tan αβ是方程2320x x -+=的两个根,则tan()αβ+的值为（ ）A ．3-B ．1-C ．1D ．32．（2012辽宁）已知sin cos αα-=,α∈(0,π),则tan α=（ ）A ．-1B ．CD ．13．（2012全国大纲）已知α为第二象限角,sin cos αα+=,则cos 2α= （ ）A ．3-B ．9-C ．9 D ．34．（2012江苏）在ABC ∆中,已知3AB AC BA BC =.(1)求证:tan 3tan B A =;(2)若cos C =求A 的值. 5．（2011广东）1()2sin(),36f x x x R π=-∈已知函数5(1)()4f π求的值; 106(2),0,,(3),(32),cos()22135f f ππαβαβπαβ⎡⎤∈+=+=+⎢⎥⎣⎦设求的值.5.5 三角恒等变换考点诠释例题精析例1 化简（1）sin 2(1tan tan )2⋅+⋅x x x（2）(sin 2cos 21)(sin 2cos 21)sin 4ααααα+--+（3）22221sin sin cos cos cos 2cos 22αβαβαβ+-思维引领从角入手，复角转化为单角；从名入手，异名化同名；从幂入手，利用降幂公式先降次.2tan2α, ,精辟分析解 （1）sin 1cos sin 2(1tan tan )2sin cos (1)2cos sin x x xx x x x x x-⋅+⋅=+⋅ 2sin (cos 1cos )2sin .x x x x =⋅+-=（2）(sin 2cos 21)(sin 2cos 21)sin 4ααααα+--+22sin 2(cos 21)sin 4ααα--=22sin 2cos 22cos 212sin 2cos 2ααααα-+-=22cos 22cos 22sin 2cos 2αααα-+=1cos 2sin 2αα-=22sin 2sin cos ααα= tan α=（3）22221sin sin cos cos cos 2cos 22αβαβαβ+-1cos 21cos 21cos 21cos 21cos 2cos 222222αβαβαβ--++=⋅+⋅-111(1cos 2cos 2cos 2cos 2)(1cos 2cos 2cos 2cos 2)cos 2cos 2442αβαβαβαβαβ=+--++++-12=方法规律总结复角化单角；异名化同名，遇到平方要降次，这是三角恒等变化中常用的方法.误区警示化简时，由于侧重点不同，出发点不同，方式有很多种，熟记并灵活运用公式是关键. 例2 （1）若,αβ是锐角，且11sin sin ,cos cos 22αβαβ-=--=,求tan()αβ-. （2）已知,(0,)αβπ∈，且11tan(),tan 27αββ-==-，求2αβ-的值.思维引领（1）因为sin()tan()cos()αβαβαβ--=-，关键求sin()αβ-与cos()αβ-.（2）配角法：()ααββ=-+，()2αβααβ-=+-精辟分析（1）由11sin sin ,cos cos 22αβαβ-=--= 两式平方相加，得122cos cos 2sin sin 2αβαβ--= 即122cos()2αβ--=3cos()4αβ∴-=,αβ是锐角，且1sin sin 02αβ-=-<02παβ∴<<<02παβ∴-<-<sin()αβ∴-==-sin()tan()cos()αβαβαβ-∴-==- （2）tan()tan tan tan[()]1tan()tan αββααββαββ-+=-+=--111270113127-==>+⨯ 02πα∴<<又22122tan 33tan 2011tan 41()3ααα⨯===>-- 022πα∴<<31tan 2tan 47tan(2)1311tan 2tan 147αβαβαβ+-∴-===+-⨯1tan 07β=-< ,2πβπ∴<<则20παβ-<-<324αβπ∴-=-.方法规律总结“给值求值”，即给出某些角的三角比值，求另外一些角的三角比值，关键在于“变角”，使其相同或具有某种关系.“给值求角”：实质上也转化为“给值求值”，关键也是变角，把所求角用含已知角的式子表示，由所得的三角比值结合角的区间求得角.误区警示给值求值时，关键在于变角，使其相同或具有某种关系；“给值求角”时，一定要注意所求角的范围，防止漏解或多解.例3 求证 32sin tantan 22cos cos 2x x xx x-=+. 思维引领“凑角法”：3131,22222x x x x x x =-=+或切割化弦 精辟分析解 32sin 2sin 2233cos cos 2cos cos 2222x x x x x x x x x ⎛⎫- ⎪⎝⎭=+⎛⎫⎛⎫-++ ⎪ ⎪⎝⎭⎝⎭332(sincos cos sin )222232cos cos22x x x xx x -=3sin sin322tan tan 322cos cos 22x x x x x x =-=-. 方法规律总结对三角条件恒等式的证明，我们要注意观察分析条件恒等式与目标恒等式的异同，要加强“目标意识”.即在恒等变形的过程中，要“盯住”目标，尽量向目标恒等式靠拢.其常用方法有：直接法、代入法、换元法等.误区警示在角出现过多的情况下，注意寻找各个角之间的关系，统一角或者是名.拓展训练一、填空题1．cos72cos36-=__________________. 2．已知x 为第四象限角，7cos 25x =，则tan 2x=_________. 3．2cos 2sin 21cos cos xx x x=+____________________. 4．2cos 1tan2tan2ααα=-_________________.5．已知sin()sin()m αβαβ+-=，则22cos cos ____________αβ-=. 6．已知7cos 28x =-，则22tan sin x x =_______________. 二、选择题7．设78,cos2t θπθπ<<=，则sin4θ等于（） （A（B ）（C（D ）8．若sin 1,1cos 2x x =+则sin cos x x +等于（ ）（A ）75 （B ）79 （C ）1118 （D ）1318三、解答题9．（14)παπ<<.（2）已知3sin 25θ=，且04πθ<<，求22cos sin 12)4θθπθ--+.10．当1cos ,12α⎡⎫∈⎪⎢⎣⎭时，求tan (sin tan )2ααα+的最大值．11.是否存在,(0,)2παβ∈，使得下列两式（1）223αβπ+=（2）tan tan 22αβ=-同时成立？12.已知,(0,)2παβ∈，且3sin 2sin αβ=，3cos 2cos 3αβ+=，求2αβ+的值.五年高考试题1．（2010上海）已知02x π<<，化简：2lg(cos tan 12sin ))]lg(1sin 2)24x x x x x π⋅+-+--+.2．（2011辽宁）设sin 1+=43πθ（），则sin 2θ= （ ） A ．79- B ．19- C ．19 D ．793．（2011重庆）已知1sin cos 2α=+α，且0,2π⎛⎫α∈ ⎪⎝⎭，则c o s 2s i n 4πα⎛⎫α- ⎪⎝⎭的值为__________． 4．（2012福建）某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.(1)2sin 13cos17sin13cos17︒+︒-︒︒ (2)2sin 15cos15sin15cos15︒+︒-︒︒ (3)2sin 18cos12sin18cos12︒+︒-︒︒ (4)2sin (18)cos48sin(18)cos48-︒+︒--︒︒ (5)2sin (25)cos55sin(25)cos55-︒+︒--︒︒ Ⅰ 试从上述五个式子中选择一个,求出这个常数Ⅱ 根据(Ⅰ)的计算结果,将该同学的发现推广三角恒等式,并证明你的结论.5．（2012广东）(三角函数)已知函数()2cos 6f x x πω⎛⎫=+ ⎪⎝⎭(其中0ω>x ∈R )的最小正周期为10π. (Ⅰ)求ω的值;(Ⅱ)设α、0,2πβ⎡⎤∈⎢⎥⎣⎦,56535f απ⎛⎫+=- ⎪⎝⎭,5165617f βπ⎛⎫-= ⎪⎝⎭,求()cos αβ+的值.5.6 正弦定理与余弦定理考点诠释1．正弦定理R CcB b A a 2sin sin sin ===（R 为ABC ∆外接圆的半径） （1）正弦定理的变形公式2sin ,2sin 2sin a R A b R B,c R C === sin ,sin ,sin 222a b c A B C R R R=== sin :sin :sin ::A B C a b c = sin sin sin ,,sin sin sin A a B b C cB bC c A a=== （2）正弦定理所使用的题型①已知两角和任一边，求其它两边和第三角； ②已知两边和一边的对角，求第三边和其它两角；已知三角形两边及其一边的对角解三角形时，利用正弦定理，但要注意判断三角形解的情况.这类问题可能有一解、两解或无解的情况. 2. 余弦定理三角形任一边的平方等于其它两边的平方和再减去这两边与夹角余弦的乘积的两倍．即在ABC ∆中：222cos a b c 2bc A =+- 222cos b a c 2ac B =+- 222cos c a b 2ab C =+-另一种形式：222c o s 2b c a A bc +-=222cos 2a c b B ac +-=222cos 2a b c C ab+-=应用余弦定理，可以解决如下有关三角形的问题：（1）已知两边及它们的夹角，求第三边和其它两个角； （2）已知三边，求三角形的三内角． 3．三角形形状的判断由已知，利用三角形中的主要知识点，特别是角的关系和边角关系，推出满足题设条件的三角形的形状.判断三角形的形状的常用方法是：把已知的等式都化为角的等式或者都化为边的等式. 4．正弦定理、余弦定理的综合运用在高考中，平面向量往往渗透在三角函数和解斜三角形中，通过平面向量的数量积、平行、垂直等条件叙述题意，本质上仍是考查三角函数或解三角形的内容，解答时注意问题的转化.例题精析例1 在ABC ∆中（1）已知2,,43b A B ππ===，求,,C a c .（2）已知1,2,a=b A 6π==，求B .（3）已知2,b A 6π==，求B .（4）已知24,3a=b A π==，求B .思路引领正弦定理的直接应用.精辟分析（1）由正弦定理sin sin a b A B =，得sin sin 3b A a B == 512C A B ππ∴=--=由sin sin b c B C =，得sin sin b C c B ==. （2）由正弦定理sin sin a b A B =，得sin 1B =，得2B π=.（3）由正弦定理sin sin a b A B =，得sin B =，b a >得34B π=或4B π=. （4）同上，6B π=方法规律总结通过已知边、角求解未知边、角的问题，关键是要正确分析边、角的关系，熟练掌握大边对大角、三角形的内角和为π以及在在(0,)π内反正弦的角的个数等知识，并加以灵活运用.误区警示要根据大边对大角，判断在(0,)π内反正弦的角的个数，防止漏解或多解.例2 在ABC ∆中，已知 2222()sin()()sin()a b A B a b A B +-=-+，试判断三角形的形状.思维引领利用正弦或余弦定理，将角转化为边或将边转化为角.精辟分析解法1 由已知得[][]22sin()sin()sin()sin()a A B A B =b A B A B --+---+222cos sin 2cos sin a A B b B A ∴=由正弦定理得22sin cos sin sin cos sin A A B B B A ∴=()sin sin sin cos sin cos 0A B A A B B ∴-=sin 2sin 2A B ∴=由0A B π<+<，得22A B =或22A B π=-所以ABC ∆是等腰三角形或直角三角形.解法2 同上可得222cos sin 2cos sin a A B b B A =由正弦、余弦定理，可得2222222222b c a a c b a b b a bc ac+-+-=22222222()()a b c a b a c b ∴+-=+-即22222()()0a b c b a ∴---=a b ∴=或222c b a =+所以ABC ∆是等腰三角形或直角三角形.方法规律总结从解题方法来看，判断三角形的形状，一般有“边化角”和“角化边”两种方法.误区警示不能边角混用.例3 在ABC ∆中，,,a b c 分别是角,,A B C 所对的边，且274sin cos 222B C A +-=. （1）求角A 的大小；（2）若3a b c =+=，求b 和c 的值.思维引领对于解三角形中有关正、与弦定理得综合问题，要先把已知条件进行处理，再适时地选择和运用正弦、余弦定理.精辟分析解 （1）由274sincos 222B C A +-=及A B C π++=，得 2272[1cos()]2cos 1,4(1cos )4cos 52B C A A A -+-+=+-=即24cos 4cos 10A A -+=1cos 2A ∴=0A π<<3A π∴=（2） 由余弦定理，得222cos 2b c a A bc +-=1cos 2A = 222122b c a bc +-∴=()223b c a bc ∴+-=将3a b c =+=代入上式得2bc =由32b c bc +=⎧⎨=⎩得12b c =⎧⎨=⎩或21b c =⎧⎨=⎩方法规律总结本例通过二倍角公式，得到一个关于余弦值得一元二次方程，再结合三角形内角关系和余弦定理求出边长，本例把正弦、余弦定理和三角恒等变换结合起来，从而解决相应的解三角形的一系列问题.误区警示要结合三角形本身具有的内角关系.拓展训练一、填空题1．在ABC ∆中，已知60,1,ABC A b S ︒∆==sin sin sin a b cA B C++=++___________.2．在ABC ∆中，已知60A ︒=，且最大边长和最小边长分别是方程27110x x -+=的两个根，则第三边的长为_________.3．在ABC ∆中，60,1),C a b c ︒=+==A 等于_________. 4．在ABC ∆中，1,2AB BC ==，则C 的取值范围是____________________.5．在ABC ∆中， 222,23,a b c bc b c a =++==ABC S ∆=__________. 6．在ABC ∆中，已知222sin sin sin sin sin A B B C C =++，则A =___________. 7．在ABC ∆中，,,a b c 分别是内角,,A B C 所对边长，若cos cos a Bb A=，则ABC ∆的形状为___ ______. 二、选择题8．在ABC ∆中，已知三边,,a b c 满足()()3a b+c a b c ab ++-=，则C 等于（ ） （A ）15︒（B ）30︒（C ）45︒（D ）60︒9．在ABC ∆中，已知s i n :s i n :s i 1:1:2A B C =，且12ABC S ∆=，则A B B C B C C A C ⋅+⋅+⋅的值是（ ）（A ）2 （B （C ）2- （D ）。