[高中数学]10B-5-教师-任意角的三角比

芯衣州星海市涌泉学校2021届高三数学专题教案：任意角的三角比一、知识梳理1、1弧度的角：弧长等于半径的圆弧所对的圆心角叫做1弧度的角2、角度与弧度的换算：18010π=弧度，1弧度=0180⎪⎭⎫ ⎝⎛π 3、任意角⎪⎩⎪⎨⎧零角负角正角，会写出终边一样的角的集合4、弧长公式、扇形的面积公式180r n r l πα==，360212122r n r lr s πα===，其中n ,α分别是扇形的圆心角的弧度制大小，和角度制大小，r 是扇形所在的圆的半径5、任意角的三角比的定义：设),(y x P 是角α的终边上异于原点的点，OP r =，那么yr x r y x x y r x r y ======ααααααcsc ,sec ,cot ,tan ,cos ,sin 6、单位圆的定义及三角函数线的定义二、例题讲解例1．根底练习（1） 判断以下角是第几象限的角①05460-②π792③π8193-④03815 〔2〕写出满足以下条件的角的集合①终边在x 轴上的角的集合终边在y 轴上的角的集合终边在坐标轴上的角的集合终边在二、四象限的角平分线上的角的集合②βα,的终边关于直线x y =对称，且65πα=，那么=β例2、α是第一象限角，试求〔1〕2α的终边所在的象限 〔2〕3α的终边所在的象限 例3、角θ的终边上一点),3(m P -，且m 42sin =θ，求θcos 和θtan 的值 例4、利用单位圆求满足以下条件的θ的取值范围〔1〕23sin >θ〔2〕22cos ,21sin ><θθ且〔3〕1tan -<θ 例5、求周长为20cm 的扇形面积的最大值，并计算当扇形面积最大时，扇形的圆心角的弧度数。

三、稳固练习1、将411π-表示为()Z k k ∈+θπ2，使θ最小的值是θ。

2、圆内一条弦的成等于半径，这条弦所对的圆心角为〔〕A 等于1弧度B 大于1弧度C 小于1弧度D 无法判断3、点()4.-x M 在角α的终边上，且0<x ，54sin -=α，那么αcos =。

三角比全章基础知识归纳1、常见的角度与弧度的相互转化2、扇形的弧长与面积角度值下．．．．的弧长公式与面积公式（其中n 为扇形的圆心角的角度数，R 为扇形半径） 弧长公式：________=l ；面积公式：________=S ；弧度制下．．．．的弧长公式与面积公式 弧长公式：________=l ；面积公式：________=S ；3、一些特殊角的三角比值4、各三角比在每个象限的符号5、诱导公式（奇变偶不变，符号看象限） 第1组()=+απk 2sin ____________________；()=+απk 2cos ____________________； ()=+απk 2tan ____________________；()=+απk 2cot ____________________；第2组()=-αsin ____________________；()=-αcos ____________________； ()=-αtan ____________________；()=-αcot ____________________；第3组()=-απsin ____________________；()=-απcos ____________________； ()=-απtan ____________________；()=-απcot ____________________；第4组()=+απsin ____________________；()=+απcos ____________________； ()=+απtan ____________________；()=+απcot ____________________；第5组=⎪⎭⎫ ⎝⎛-απ2sin ____________________；=⎪⎭⎫⎝⎛-απ2cos ____________________； =⎪⎭⎫ ⎝⎛-απ2tan ____________________；=⎪⎭⎫⎝⎛-απ2cot ____________________； 第6组=⎪⎭⎫ ⎝⎛+απ2sin ____________________；=⎪⎭⎫⎝⎛+απ2cos ____________________； =⎪⎭⎫ ⎝⎛+απ2tan ____________________；=⎪⎭⎫⎝⎛+απ2cot ____________________； 6、同角三角比关系 【商数关系】________cos sin =αα； ________sin cos =αα； 【平方关系】=+αα22cos sin ____________________； =+α2t a n 1____________________；=+α2cot 1____________________；【倒数关系】=αsec ____________________；αcsc ________________；=αtan ____________________； 三点总结：①切割化弦，“切”通过商数关系化为“弦”，“割”通过倒数关系化为“弦”； ②弦化切，一般和“齐次式”有关，通过分式上下同时除以cos 或2cos 得到“切”； ③1的代换，通过平方关系，将1带换成所需的三角比；7、三角恒等变换【两角和与差的正弦、余弦、正切公式】()=+βαsin ____________________； ()=-βαsin ____________________； ()=+βαcos ____________________； ()=-βαcos ____________________；()=+βαtan ____________________； ()=-βαtan ____________________；【辅助角公式】sin cos a b αα+=_____________________________________________；常见类型：⎪⎭⎫ ⎝⎛±=±4sin 2cos sin πααα⎪⎭⎫ ⎝⎛±=±6sin 2cos sin 3πααα⎪⎭⎫ ⎝⎛±=±3sin 2cos 3sin πααα【倍角公式】=α2sin ____________________；=α2cos ____________________=____________________=____________________；=α2tan ____________________；【半角公式】=2sinα____________________； =2cosα____________________；=2tanα____________________； =2cotα____________________；=2tanα____________________=____________________；8、其他公式及恒等变换 【降幂公式】=2sin 2α____________________； =2cos 2α____________________；【升幂公式】=+αcos 1____________________； =-αcos 1____________________； =+αsin 1____________________； =-αsin 1____________________； =1____________________； =αsin ____________________；【万能置换公式】=αsin ___________________； =αcos ___________________；=αtan ___________________；【常见公式变形】_________cos 1=+α；_________cos 1=-α； _________2sin 1=+α；_________2sin 1=-α _______tan 1tan 1=-+αα；_______tan 1tan 1=+-αα；【常见角的变换】()ββαα-+=；22αα⋅=；⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛+=απαππ442； ()()βαβαα-++=2；()()βαβαβ--+=2；⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=+βαβαβα222；⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+=-βαβαβα2229、解三角形【三角形面积计算公式】=S ___________________=___________________=___________________；18、【正弦定理公式】=Aasin ________=_______=__________=_________； 19、【余弦定理公式】=2a ___________________； =A cos ___________________； =2b ___________________； =B cos ___________________； =2c ___________________； =C cos ___________________；10、三角形中常见结论。

视频1：在直角坐标系中角的终边上任意一点的坐标来定义任意角的三角比。

设(),P x y 是角α终边上的任意一点（不重合于角的顶点），则P 点到坐标原点O 的距离为r OP ==，定义:①正弦：sin α=；②余弦：cos α=；③正切：tan α=； ④余割：csc α=；⑤正割：sec α=；⑥余切：cot α=；Note ：①任意角的三角比仅与角的终边位置有关，而与终边上所取点P 的位置 。

②当角α的终边落在y 轴时，(),P x y 是角α终边上的任意一点（不重合于角的顶点），此时x =，则cos α=，且tan α与sec α ；③当角α的终边落在x 轴时，(),P x y 是角α终边上的任意一点（不重合于角的顶点），此时y =，则sin α=，且 与 无意义；④角α的终边无论落在什么位置，(),P x y 是角α终边上的任意一点（不重合于角的顶点），此时0r =>，故sin α与cos α总是存在的。

⑤22sin cos αα+=练习：已知角α的终边上一点()12,5P -，求角α的六个三角比的值。

6分钟视频2：正弦函数在第一象限为 ，第二象限为 ，第三象限为 ，第四象限为 ； 余弦函数在第一象限为 ，第二象限为 ，第三象限为 ，第四象限为 ； 正切函数在第一象限为 ，第二象限为 ，第三象限为 ，第四象限为 。

练习：确定下列三角函数值的符号。

①cos 250︒；②sin 4π⎛⎫-⎪⎝⎭；③()tan 672︒-；④tan 3π 5分钟视频3：练习：根据下列条件确定角θ属于哪个象限： ①sin cos 0θθ>；②sin 0θ<且tan 0θ> 2分钟视频4：从开始--------05:27结束（将开头删掉）。

设α是一个任意角，它的终边与单位圆交于点(),P x y ，那么 ①正弦：sin α=；②余弦：cos α=；③正切：tan α=； ④余割：csc α=；⑤正割：sec α=；⑥余切：cot α=；Note1：常见的三角函数的定义域与值域①正弦函数sin y x =，定义域为 ，值域为 。

任意角的三角比三角比的基本概念一、知识整理： 1.角的概念的推广(1)角的分类:正角(逆转) 负角(顺转) 零角(不转)(2)终边相同角:0360()2()k k Z k k Z βαβπα=⋅+∈=+∈(3)直角坐标系中的象限角与坐标轴上的角。

2.角的度量(1)弧度制的概念：长度等于半径的弧所对的圆心角为1弧度。

(2)角度制与弧度制的换算: 180180ππ⨯⨯角度弧度(3)弧长公式:l r α=⋅ 扇形面积公式:21122S lr r α== 3.任意角的三角函数yxx y x rr x y rr y ======ααααααcot tan sec cos csc sin注:要熟记各象限的角的三角比的符号。

二、例题：例1．给出下列命题，其中正确的是 ( D ) （1）弧度角与实数之间建立了一一对应 （2）终边相同的角必相等 （3）锐角必是第一象限角 （4）小于900的角是锐角 （5）第二象限的角必大于第一象限角sin αtan ααA （1）B （1）（2）（5）C （3）（4）（5）D （1）（3） 例2．已知角︒=45α；（1）若角β与角α有相同的终边，且7200β-︒≤≤︒，求角β；（2）集合⎭⎬⎫⎩⎨⎧∈︒+︒⨯==Z k k x x M ,451802|，⎭⎬⎫⎩⎨⎧∈︒+︒⨯==Z k k x x N ,451804|，那么两集合的关系是什么？解析：（1）所有与角α有相同终边的角可表示为：)(36045Z k k ∈︒⨯+︒， 则令 ︒≤︒⨯+︒≤︒-036045720k ， 得 ︒-≤︒⨯≤︒-45360765k解得 36045360765-≤≤-k 从而2-=k 或1-=k代回︒-=675β或︒-=315β（2）因为{}Z k k x x M ∈︒⨯+==,45)12(|表示的是终边落在四个象限的平分线上的角的集合；而集合{}Z k k x x N ∈︒⨯+==,45)1(|表示终边落在坐标轴或四个象限平分线上的角的集合，从而，M N 是的真子集。

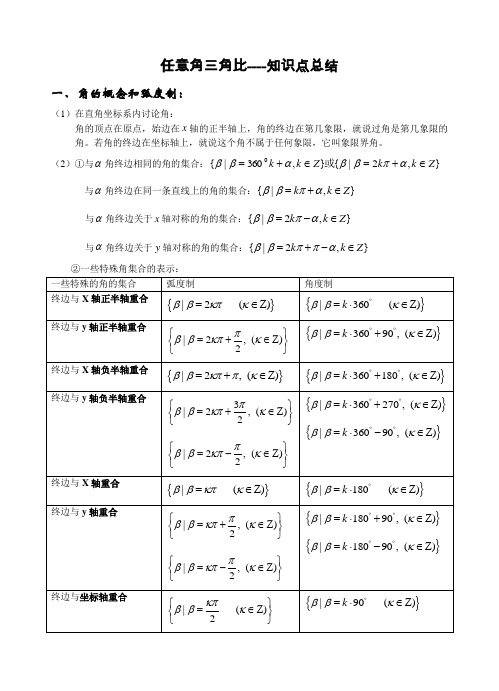
任意角三角比----知识点总结一、角的概念和弧度制：（1）在直角坐标系内讨论角：角的顶点在原点，始边在x 轴的正半轴上，角的终边在第几象限，就说过角是第几象限的角。

若角的终边在坐标轴上，就说这个角不属于任何象限，它叫象限界角。

（2）①与α角终边相同的角的集合：},2|{},360|{0Z k k Z k k ∈+=∈+=απββαββ或与α角终边在同一条直线上的角的集合：{|,}k k Z ββπα=+∈ 与α角终边关于x 轴对称的角的集合：{|2,}k k Z ββπα=-∈ 与α角终边关于y 轴对称的角的集合：{|2,}k k Z ββππα=+-∈ ②一些特殊角集合的表示： 一些特殊的角的集合 弧度制角度制终边与X 轴正半轴重合 {}|2()ββκπκ=∈Z{}|360()k ββκ︒=⋅∈Z 终边与y 轴正半轴重合|2,()2πββκπκ⎧⎫=+∈Z ⎨⎬⎩⎭{}|36090,()k ββκ︒︒=⋅+∈Z 终边与X 轴负半轴重合 {}|2,()ββκππκ=+∈Z{}|360180,()k ββκ︒︒=⋅+∈Z终边与y 轴负半轴重合3|2,()2πββκπκ⎧⎫=+∈Z ⎨⎬⎩⎭|2,()2πββκπκ⎧⎫=-∈Z ⎨⎬⎩⎭{}|360270,()k ββκ︒︒=⋅+∈Z {}|36090,()k ββκ︒︒=⋅-∈Z终边与X 轴重合 {}|()ββκπκ=∈Z{}|180()k ββκ︒=⋅∈Z 终边与y 轴重合|,()2πββκπκ⎧⎫=+∈Z ⎨⎬⎩⎭ |,()2πββκπκ⎧⎫=-∈Z ⎨⎬⎩⎭{}|18090,()k ββκ︒︒=⋅+∈Z {}|18090,()k ββκ︒︒=⋅-∈Z终边与坐标轴重合|()2κπββκ⎧⎫=∈Z ⎨⎬⎩⎭{}|90()k ββκ︒=⋅∈Z终边在一、三象限的平分线上角的集合|,()4πββκπκ⎧⎫=+∈Z ⎨⎬⎩⎭{}|18045,()k ββκ︒︒=⋅+∈Z 终边在二、四象限的平分线上角的集合： 3|,()4πββκπκ⎧⎫=+∈Z ⎨⎬⎩⎭{}|180135,()k ββκ︒︒=⋅+∈Z终边在四个象限的平分线上角的集合：|,()24κππββκ⎧⎫=+∈Z ⎨⎬⎩⎭{}|9045,()k ββκ︒︒=⋅+∈Z（3）区间角的表示象限角： 所在象限 弧度制角度制第一象限 |22,()2πακπακπκ⎧⎫<<+∈Z ⎨⎬⎩⎭{}|36036090,()k k αακ︒︒︒⋅<<⋅+∈Z第二象限 |22,()2πακπακππκ⎧⎫+<<+∈Z ⎨⎬⎩⎭{}|36090360180,()k k αακ︒︒︒︒⋅+<<⋅+∈Z第三象限 3|22,()2πακππακπκ⎧⎫+<<+∈Z ⎨⎬⎩⎭{}|360180360270,()k k αακ︒︒︒︒⋅+<<⋅+∈Z第四象限3|222,()2πακπακππκ⎧⎫+<<+∈Z ⎨⎬⎩⎭|22,()2πακπακπκ⎧⎫-<<∈Z ⎨⎬⎩⎭{}|360270360360,()k k αακ︒︒︒︒⋅+<<⋅+∈Z{}|36090360,()k k αακ︒︒︒⋅-<<⋅∈Z（4）正确理解角：要正确理解“o o 90~0间的角”=090α︒︒<<“第一象限的角”=36036090,()k k ακ︒︒︒⋅<<⋅+∈Z ；“锐角”=090α︒︒<<； “小于o90的角”= 90α︒<；（5）由α的终边所在的象限，通过二等分每个象限来判断2α所在的象限；三等分每个象限 来判断3α所在的象限 （6）弧度制：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零；任一已知角α的弧度数的绝对值rl =||α，其中l 为以角α作为圆心角时所对圆弧的长，r 为圆的半径。

高三数学-高考复习讲义-任意角的三角比1．角的概念的推广（1）正角，负角和零角.用旋转的观点定义角，并规定了旋转的正方向，就出现了正角，负角和零角，这样角的大小就不再限于00到3600的范围.（2）象限角和轴线角.象限角的前提是角的顶点与直角坐标系中的坐标原点重合，始边与x 轴的非负半轴重合，这样当角的终边在第几象限，就说这个角是第几象限的角，若角的终边与坐标轴重合，这个角不属于任一象限，这时也称该角为轴线角.（3）终边相同的角，具有共同的绐边和终边的角叫终边相同的角，所有与角α终边相同的角（包含角α在内）的集合为{}Z k k ∈⋅+=,360 αββ. （4）角α在“0到 360”范围内，指 3600<≤α.2． 弧度制（1）角度制与弧度制.用一个周角的3601（1度的角）作为度量单位来度量角的制度叫角度制.角度制在形数结合解决问题时会受到一定限制.弧度的角作为度量单位来度量角的制度叫弧度制.对于角α，以顶点O 为圆心，分别以'r r 、和'l ，则α==''r l r l 取弧的半径无关.（2集合与角的集合之间建立起一种一一对应的关系.（3）角度与弧度的换算.只要记住rad π=180 由rad π=⨯=1180180，rad 1801π=.由 1801=⨯=rad rad ππ，30.571801≈⎪⎭⎫ ⎝⎛=πrad .应熟记一些特殊角的度数和弧度数.在书写时注意不要同时混用角度制和弧度制，如：“ 3602⋅+k π”和“πk 290+ ”的写法都是不妥当的.（4）弧长公式和扇形面积公式.由定义，在弧度制中，半径为r ，弧度数为rad α的弧长r l α=.在角度制中，半径为r 、圆心角为n 的弧长r n r n l 1802360ππ=⋅=. 在弧度制中，半径为r ，弧度数为rad α的扇形面积r l r r S 2121222==⋅=αππα. 在角度制中，半径为r ，圆心角为n 的扇形面积22360360r n r n S ππ=⋅=. 3．任意角的三角比 三角比的定义在直角坐标系中，设α是一个任意角，α终边上任意一点P （除了原点）的坐标为(,)x y ，它与原点的距离为(0)r r =，那么 ⑴ 比值y r 叫做α的正弦，记作sin α，即sin y r α=； ⑵ 比值x r 叫做α的余弦，记作cos α，即cos x rα=； ⑶ 比值()0y x x≠叫做α的正切，记作tan α，即tan y x α=．三角比的符号由三角函数的定义，以及各象限内点的坐标的符号，我们可以得知（如下表）：① 正弦值yr 对于第一、二象限为正（0,0y r >>），对于第三、四象限为负（00y r <>，）；② 余弦值xr 对于第一、四象限为正（0,0x r >>），对于第二、三象限为负（00x r <>，）；③ 正切值()0yx x≠对于第一、三象限为正（,x y 同号），对于第二、四象限为负（x y ，异号）．注意：余切、正割、余割自行推导4．单位圆与三角函数线（1）单位圆：一般地，我们把半径为1的圆叫做单位圆．如下图，角α的终边与单位圆交于点()P x y ，．过P 作x 轴的垂线，垂足为M ．过点(10)A ，作单位圆的切线，它与角α的终边或其反向延长线交于点T ．根据三角函数的定义，我们有：|||||sin |MP y α==；|||||cos |OM x α==；|||tan |AT α=．坐标轴是规定了方向的直线，直角坐标系内的点的坐标与坐标轴的方向有关．因此一个自然的想法就是以坐标轴的方向来规定线段OM MP ，的方向，以使它们的取值与P 点的坐标联系起来．当角α的终边不在坐标轴上时，以O 为始点，M 为终点，规定：当线段OM 与x 轴同向时，OM 的方向为正，且有正值x ；当线段OM 与x 轴反向时，OM 的方向为负，且有负值x ．其中x 为P 点的横坐标．所以无论哪一种情况都有cos OM x α==．同理，可以得到，无论哪一种情况都有sin MP y α==；tan yAT xα==．有向线段：像MP ，OM ，AT 这种被看作带有方向的线段叫做有向线段．规定：与坐标轴方向一致时为正，与坐标方向相反时为负．（2）与单位圆有关的有向线段，OM ，AT 分别叫做角α的正弦线、余弦线、正切线．统称为三角函数线．① 三条有向线段的位置：正弦线为α的终边与单位圆的交点到x 轴的垂直线段；余弦线在x 轴上；正切线在过单位圆与x 轴正方向的交点的切线上，三条有向线段中两条在单位圆内，一条在单位圆外．② 三条有向线段的方向：正弦线由垂足指向α的终边与单位圆的交点；余弦线由原点指向垂足；正切线由切点指向与α的终边的交点．③ 三条有向线段的书写：有向线段的起点字母在前，终点字母在后． 6．终边相同角的三角函数值 公式一：ααsin )360sin(=⋅+k ， ααcos )360cos(=⋅+k ， ααtan )360tan(=⋅+k . )(Z k ∈也称为诱导公式一，利用公式一可以把任意角的三角函数化为0到360角的三角函数.一、角的概念的推广1、角的概念【例1】若时针走过2小时40分，则分针走过的角是多少？【例2】求经过下列时间，时钟的分针所转过的角度：（1）15分钟；（2）1小时20分钟.2、终边相同的角【例3】找出与下列各角终边相同的角的一般形式，指出它们是哪个象限的角，并找出终边相同的角中绝对值最小的角：（1） 1000； （2） 700-； （3） 950- .【例4】写出下列各边相同的角的集合S ，并把S 中适合不等式360720β-≤≤的元素β 写出来： （1）60； （2）21-； （3）36314'．【例5】设 {| 36045,}A k k Z αα=⋅︒+︒∈＝，{| 360225,}B k k Z αα=⋅︒+︒∈＝{| 18045,}C k k Z αα=⋅︒+︒∈＝ ， {| 360135,}D k k Z αα=⋅︒-︒∈＝{| 36045 360225,}E k or k k Z ααα=⋅︒+︒=⋅︒+︒∈＝，则相等的角集合为_ _。

任意角的三角比教案
三角比是指三角形中各边的比值，通常包括正弦、余弦和正切。

在教学这个概念时，可以从以下几个角度进行教案设计：
1. 概念介绍，首先，要介绍三角形的基本概念，包括顶点、边、角度等，并引入三角比的概念。

可以通过图示和实际示例来让学生
直观理解三角比的含义和作用。

2. 正弦、余弦和正切的定义，分别介绍正弦、余弦和正切的定义，以及它们在直角三角形和任意角三角形中的计算方法。

可以通
过几何图形和实际问题来说明三角比的定义和计算方法。

3. 三角比的性质，介绍三角比的基本性质，如正弦、余弦和正
切的周期性、奇偶性等，以及它们之间的关系。

通过数学推导和实
例演示来让学生理解三角比的性质。

4. 三角比的应用，介绍三角比在实际生活和工程中的应用，如
测量高度、距离、角度等。

可以通过实际案例和问题让学生体会三
角比在实际中的重要性和作用。

5. 综合练习，设计一些综合性的练习题，包括计算三角比、证明三角比的性质、解决实际问题等，以帮助学生巩固所学的知识和技能。

在教学过程中，可以结合多媒体教学、小组讨论、实验演示等多种教学方法，让学生在实践中感受三角比的奥妙，提高他们的学习兴趣和能力。

同时，教师应该注重引导学生思考，培养他们的数学思维和解决问题的能力，使他们能够灵活运用三角比解决实际问题。

任意角的三角比讲义一、角度的定义和表示1. 角度的定义角度是度量两条射线之间旋转的大小。

角度的度量单位是度（°）或弧度（rad）。

2. 角度的表示角度可以用三种形式进行表示：度（°），分（’）和秒（’’）。

例如，一个角度为60度15分20秒，则可以表示为60°15’20’’。

二、任意角的三角比1. 任意角任意角是指一个角度可以不是90度的角度。

2. 正弦、余弦、正切函数在任意角的情况下，我们仍然可以计算三角函数的值。

例如，对于一个任意角A，我们可以定义其正弦、余弦和正切函数分别为SIN(A)、COS(A)和TAN(A)。

其中，正弦函数的值等于对边与斜边的比值，余弦函数的值等于邻边与斜边的比值，正切函数的值等于对边与邻边的比值。

3. 三角函数的性质在任意角的情况下，三角函数仍然具有一些重要的性质。

3.1 周期性正弦函数和余弦函数的周期均为360度或2π弧度，即它们在每经过360度或2π弧度时会重复一次。

正切函数的周期为180度或π弧度，即它们在每经过180度或π弧度时会重复一次。

3.2 值域正弦函数和余弦函数的值域均为[-1,1]，即它们的函数值均在这个范围内。

正切函数的值域为所有实数，即正切函数可以取到任意实数的值。

4. 三角函数的应用在实际问题中，三角函数广泛应用于各种领域，如物理、工程、地理等。

例如，在三角学中，我们可以使用正弦函数和余弦函数来计算两个角度之间的距离、高度等。

在物理学中，我们可以使用三角函数来计算力的大小和方向等问题。

三、小结任意角的三角比是三角函数的重要部分，它在数学、物理和工程等领域都有着广泛的应用。

我们需要了解三角函数的定义、性质和应用，以便能够在实际问题中进行计算和分析。