3任意角三角比

任意角的三角比一、基础知识熟练记忆1、任意角的三角比——对于任意角的三角比，我们利用平面直角坐标系来进行研究。

（1）设α是一个任意角，在α的终边上任取（异于原点的）一点P （x,y ） 则点P 与原点的距离02222>+=+=y x y x r（2）比值r y叫做α的正弦 记作： r y =αsin 比值r x叫做α的余弦 记作： r x =αcos 比值x y叫做α的正切 记作： xy =αtan 比值y x叫做α的余切 记作： yx =αcot 比值x r叫做α的正割 记作： x r =αsec 比值y r叫做α的余割 记作： yr =αcsc 根据相似三角形的知识，对于终边不在坐标轴上确定的角α， 上述六个比值都不会随P 点在α的终边上的位置的改变而改变。

当角α的终边在纵轴上时，即Z)(2∈+=k k ππα时，终边上任意一点P 的横坐标x 都为0，所以tan α、sec α无意义；当角α的终边在横轴上时，即α＝ｋπ（ｋ∈Z ）时， 终边上任意一点P 的纵坐标ｙ都为0，所以cot α、csc α无意义。

几个需要注意的问题：① 凡是终边相同的角的三角函数值相等。

sin(2k π+α)=sin α cos(2k π+α)=cos α tan(2k π+α)=tan α cot(2k π+α)=cot α② 0>r 而x,y 的正负是随象限的变化而不同，故三角函数的符号应由象限确定。

第一象限：0,0.>>y x∴sin α>0，cos α>0，tan α>0，cot α>0 第二象限：0,0.><y x∴sin α>0，cos α<0，tan α<0，cot α<0O A M P Txyα的终边 x yO A M T yOAM xyOAM TPα的终边第三象限：0,0.<<y x∴sin α<0，cos α<0，tan α>0，cot α>0 第四象限：0,0.<>y x∴sin α<0，cos α>0，tan α<0，cot α<0记忆法则：第一象限全为正，二正三切四余弦。

视频1：在直角坐标系中角的终边上任意一点的坐标来定义任意角的三角比。

设(),P x y 是角α终边上的任意一点（不重合于角的顶点），则P 点到坐标原点O 的距离为r OP ==，定义:①正弦：sin α=；②余弦：cos α=；③正切：tan α=； ④余割：csc α=；⑤正割：sec α=；⑥余切：cot α=；Note ：①任意角的三角比仅与角的终边位置有关，而与终边上所取点P 的位置 。

②当角α的终边落在y 轴时，(),P x y 是角α终边上的任意一点（不重合于角的顶点），此时x =，则cos α=，且tan α与sec α ；③当角α的终边落在x 轴时，(),P x y 是角α终边上的任意一点（不重合于角的顶点），此时y =，则sin α=，且 与 无意义；④角α的终边无论落在什么位置，(),P x y 是角α终边上的任意一点（不重合于角的顶点），此时0r =>，故sin α与cos α总是存在的。

⑤22sin cos αα+=练习：已知角α的终边上一点()12,5P -，求角α的六个三角比的值。

6分钟视频2：正弦函数在第一象限为 ，第二象限为 ，第三象限为 ，第四象限为 ； 余弦函数在第一象限为 ，第二象限为 ，第三象限为 ，第四象限为 ； 正切函数在第一象限为 ，第二象限为 ，第三象限为 ，第四象限为 。

练习：确定下列三角函数值的符号。

①cos 250︒；②sin 4π⎛⎫-⎪⎝⎭；③()tan 672︒-；④tan 3π 5分钟视频3：练习：根据下列条件确定角θ属于哪个象限： ①sin cos 0θθ>；②sin 0θ<且tan 0θ> 2分钟视频4：从开始--------05:27结束（将开头删掉）。

设α是一个任意角，它的终边与单位圆交于点(),P x y ，那么 ①正弦：sin α=；②余弦：cos α=；③正切：tan α=； ④余割：csc α=；⑤正割：sec α=；⑥余切：cot α=；Note1：常见的三角函数的定义域与值域①正弦函数sin y x =，定义域为 ，值域为 。

课题：_任意角的三角比__教学任务教学流程说明教学过程设计任意角的三角比一、填空：1 •根据角a终边所在的位置，写角a的集合，第二象限__________________ ，在y轴上____________ ，第二象限角平分线_____________________ ，第一、第三象限角平分线rt2 • a 在第二象限，贝U3 在第_______ 象限，2 a 在第___________ 象限3. _______________________________________________________________________ 已知角a的终边过点P (- 4m,3m) (m^ 0),则2sin a+co抄的值是 ___________________________ .4. __________________________________________ 若角a 终边在直线y = 2x上,贝V si n- , cos-，- ______________________________ ,ta n-：匚-_______ ,5 •如果角［与：的终边关于y轴对称，则cos: + COS P = _________________QA已知 sin v sin ? V -1,贝U cos - cos =答案:答案:的终边上的一点 p -9t,12t t=0，求这个角的三角比。

答案：17、设 X 「X 2 是关于x 的方程x 2+2（sin°+1）x + sin 2日=0的两个根，已知x,—x 2兰2运, 求二的取值范围。

答案：6.7、 16在（一4二，4二）上与角 终边相同的所有角为3适合条件|si n t |= — sin 鳥 的角鳥是第 _____________ 象限角8、 二］=:”是"tan 二=tan : ”的条件9、 二、选择： 下列各式结果为正值的是 A . cos2「sin 2角a 的终边过点 A .仝510、11、B . P (-4k , (cos2 3k ), )sin2C . tan3 sec2(k<0),则cosa 的值是sin 2 tan212、 如果：•是第二象限角, 那么）象限角 (A)n 或川(B)13、设B 为第二象限的角, 0 0 A . tan cot — 2I 或n 则必有（(C) I 或川 (D)「 . 0 ' 2 三、解答)e etan cot —22C . sin^ .cos —2D . sin^cosZ2 214、已知第二、 第三象限角 卄 2a —3 x 满足 cosx= ---------4 -a，求实数a 的取值范围.15、已知集合71x < k,k Z , 32B={x4 - x 2 _ 0?，求 API B 。

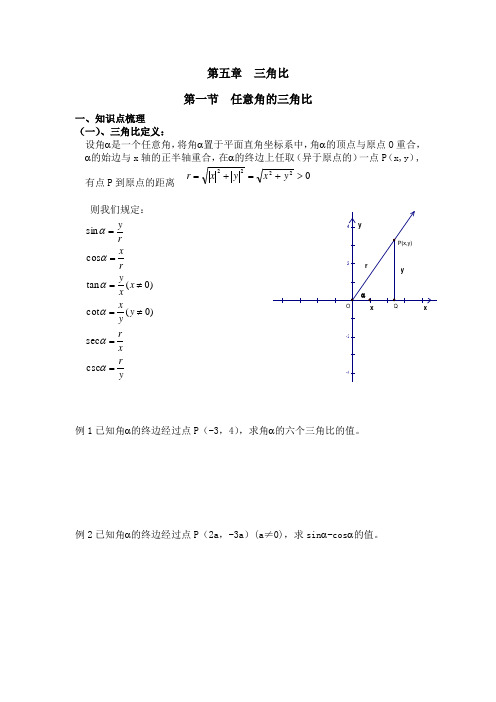
第五章 三角比 第一节 任意角的三角比一、知识点梳理 （一）、三角比定义： 设角α是一个任意角，将角α置于平面直角坐标系中，角α的顶点与原点O 重合，α的始边与x 轴的正半轴重合，在α的终边上任取（异于原点的）一点P （x,y ）, 有点P 到原点的距离 02222>+=+=y x y x r则我们规定：y rx ry y xx x yr xr y ==≠=≠===ααααααcsc sec )0(cot )0(tan cos sin例1已知角α的终边经过点P （-3，4），求角α的六个三角比的值。

例2已知角α的终边经过点P （2a ，-3a ）(a ≠0)，求sin α-cos α的值。

例3求65π的六个三角比的值。

例4应用三角比的定义证明： （1）平方关系222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= （2）倒数关系sin αcsc α=1,cos αsec α=1,tan αcot α=1, （3）商数关系sin cos tan ,cot cos sin αααααα==专题训练1、分别求0、2π、π、23π、π的三角比值。

2、分别求6π、4π、3π、65π、43π、32π的三角比值。

3、已知角α的终边与函数y=-3x 的图形重合，求角α的各三角比的值。

4、已知角α的终边与x轴重合，求cosα得值。

评注：三角比的定义是三角知识的源头，务必充分理解，灵活应用，熟练掌握。

（二）、三角函数线：1、正弦线：无论α是第几象限角，过α的终边与单位圆的交点P作x轴的垂线，交x轴于M，有向线段MP的符号与点P的纵坐标y的符号一致，长度等于｜y｜．所以有→MP=y=sinα．我们把有向线段→MP叫做角α的正弦线，正弦线是角α的正弦值的几何形式．2、余弦线：有向线段→OM叫做α的余弦线。

3、正切线：过A（1，0）点作单位圆的切线（x轴的垂线），设α的终边或其反向延长线与这条切线交于T点，那么有向线段→AT叫做角α的正切线。

任意角的三角比教案
一、教学目标
1. 理解正弦、余弦和正切的概念。

2. 掌握如何计算任意角的正弦、余弦和正切值。

3. 能够运用三角函数解决相关实际问题。

二、教学重点和难点
1. 重点：正弦、余弦和正切的概念及计算方法。

2. 难点：任意角的三角比的应用。

三、教学内容
1. 正弦、余弦和正切的定义：在直角三角形中，对于任意角A，定义如下：
正弦（sinA）= 对边/斜边，余弦（cosA）= 邻边/斜边，正切（tanA）= 对边/邻边。

2. 任意角的三角比的计算：
对于任意角A，可以通过相关公式计算其正弦、余弦和正切值。

sinA = b/c, cosA = a/c, tanA = b/a，其中a、b、c分别为直角三角形的边长。

四、教学过程
1. 引入：
通过实际问题引入正弦、余弦和正切的概念，比如航海、建筑等领域中的应用。

2. 讲解：
讲解正弦、余弦和正切的定义，并介绍如何计算任意角的三角比。

3. 示例分析：
给出一些具体的例子，让学生通过三角函数的计算，解决相关实际问题。

4. 练习：
让学生做一些相关练习，巩固所学知识。

五、教学小结
通过本节课的学习，学生能够理解正弦、余弦和正切的概念，掌握计算任意角的三角比的方法，并能够运用到实际问题中。

六、作业布置
布置相关的练习题，鼓励学生在课后复习所学知识，并思考如何应用到生活中。

七、教学反思
回顾本节课的教学过程，总结学生的学习情况，思考如何更好地教学。

5.2任意角的三角比(1)一、教学内容将角放入平面直角坐标系中，定义任意角的正弦、余弦、正切、余切、正割、余割六个三角比，探求比值中各字母的取值范围，研究正弦、余弦、正切、余切、正割、余割这六个三角比存在的条件；并根据三角比的定义，得出“终边重合的角的同一三角比的值相等”的结论及把此结论表示成为第一组诱导公式。

学会用定义求任意角的三角比；在解题中应用分类讨论的思想。

二、教学目标1、知识与技能掌握任意角的正弦、余弦、正切、余切、正割、余割的定义；通过任意三角比的定义学会对给定的角进行求三角比的值；领会三角比的大小只与角度的大小相关，学会用分类讨论的思想解决问题。

2、过程与方法通过回忆锐角三角比，感悟任意三角比的定义及相关要点；体会同一角三角比的值，不因在其终边上取点的变化而变化，从而启示在研究问题时，要能在千变万化中，抓住事物的本质属性，不被表面现象所迷惑．通过三角比定义的建立，是学生初步领会用代数方法解决几何问题的数形结合思想。

3、情感态度与价值观在整个教学过程中用运动变化的观点审视事物，用对立统一的规律揭示生活中的空间形式和数量关系。

培养学生的辩证唯物主义观点。

三、教学重点及难点重点：任意角的三角比的定义．难点：求含有字母的三角比的值，分类讨论思想方法运用。

四、教学流程五、教学过程一、情景引入回顾：初中学习了锐角的三角比，它是在直角三角形的条件下，通过角α的对边、邻边与斜边之间两两的比值来定义的.例如：sin MP OP α= cos OMOP α= tan MP OM α=cot OMMPα= 引入：前面我们对角的概念进行了扩充，并学习了弧度制，知道角的集合与实数集是一一对应的，在这个基础上，今天我们来研究任意角的三角比.把锐角α置于平面直角坐标系xOy 中，锐角α的顶点与原点O 重合，始边与x 轴的正半轴重合，那么它的终边在第一象限.易知P 在角α的终边上，设它的坐标为(,)x y，它与原点的距离0r =>，可发现作为锐角α的三角比能用其终边上的点的坐标来定义，而这种定义方法可用于定义任意角的三角比.二、学习新课1、概念形成任意角的三角比定义设α是一个任意角，在α的终边上任取一点(,)P x y （除原点）， 则P与原点的距离0r =>，PM(P α角比值ry叫做α的正弦 记作： r y =αsin比值r x叫做α的余弦 记作： rx =αcos比值xy叫做α的正切 记作： x y =αtan （,2k k z παπ≠+∈）比值y x 叫做α的余切 记作： y x=αcot （,k k z απ≠∈） 比值xr叫做α的正割 记作： xr =αsec （,2k k z παπ≠+∈）比值y r叫做α的余割 记作： yr =αcsc （,k k z απ≠∈）设问1：对于确定的角α，这六个三角比的大小与P 点在角α终边上的位置是否有关？（要求学生回答并说明理由）（利用相似三角形的知识，可以得出对于确定的角α，这六个三角比值的大小与P 点在角α的终边上的位置无关．）sin(2)sin k παα+=, cos(2)cos k παα+=tan(2)tan k παα+=, cot(2)cot k παα+=设问2：六个三角比中各个字母（x 、y 、r ）的取值有什么限制？ 设问3：根据这六个三角比的定义，是否对于任意的一个角α，它的六个三角比都存在呢？（学生探讨，给出结论）[(1) 当角α的终边在纵轴上时，即()2k k Z παπ=+∈时，终边上任意一点P 的横坐标x 都为0，所以tan α、sec α无意义；(2) 当角α的终边在横轴上时，即()k k Z απ=∈时，终边上任意一点P 的纵坐标y 都为0，所以cot α、csc α无意义.从而有：sincostanααα)(2ZkkRR∈+≠ππαcot sec csc ααα)()(2)(ZkkZkkZkk∈≠∈+≠∈≠παππαπα][说明](1) 以后我们在平面直角坐标系内研究角的问题，其顶点都在原点，始边都与x轴的非负半轴重合.(2) OP是角α的终边，至于是转了几圈，按什么方向旋转都没有要求，也只有这样，才能说明角α是任意的.(3) sinα是个整体符号，不能认为是“sin”与“α”的积，其余五个符号也是这样.(4) 三角比值只与角的大小有关.设问4、任意角三角比的定义与锐角三角比的定义的联系与区别。