5.3拉压杆应力
- 格式:pps
- 大小:749.50 KB
- 文档页数:17


直杆轴向拉伸与压缩时的应力与应变杆件的拉伸与压缩是杆件的基本变形形式之一,在机械加工中,经常会遇到直杆构件承受轴向拉伸和轴向压缩,在直杆受到轴向拉伸与压缩时会发生应力与应变。
一、直杆的轴向拉伸和轴向压缩图1(a)直杆构件受到沿轴向拉伸的力而沿轴向伸长,杆件的这种变形形式称为杆件的轴向拉伸。
图1(b) 直杆构件受到沿轴向压缩的力而沿轴向缩短,杆件的这种变形形式称为杆件的轴向压缩。
图1 直杆构件的轴向拉伸与轴向压缩受轴向拉伸与压缩的均匀直杆件受力的共同特征是作用在杆件上的外力合力的作用线与杆件轴线重合,杆件两端的外力方向相反,大小相等。
二、直杆轴向拉伸及压缩的内力和应力(一)直杆轴向拉伸及压缩的内力1.内力的定义及特点直杆受到杆件以外物体对杆件的作用力而变形时,其内部各质点之间的相互作用力将发生改变,这种由于外力作用而引起的直杆内各质点之间的相互作用力称为内力,也称为轴力,表示。
应力具有抵抗外力,阻止外力使构件继续变形的能力,随外力的增加而加大,用FN当内力达到某一限度时会引起构件的破坏。
对轴力的正负号规定如下:轴力的方向与所在横截面的外法线方向一致时,轴力为正;反之为负。
即杆受拉伸时轴力为正,受压缩时轴力为负。
2.求内力基本方法截面法是求内力的基本方法,截面法就是假想地将杆件截开,以求得内力大小的方法。
具体方法是切、留、代、平。
即假想沿指定横截面将杆切开,留下左半段或是右半段,标注荷载和反力,将抛掉部分对留下部分的作用用内力代替,对留下部分写平衡方程式求出内力值。
例如图2所示:图2 截面法为了确定其横截面m-m 上的内力,可假想沿横截面m-n 将杆截成两段,弃去右段,研究左段如图2(b )。
由于杆在拉力F 作用下处于平衡状态,所以截开后的左段(如取右段研究结果相同)仍应保持平衡,因此横截面上必须有一个力N F 作用,它是杆右段对左段的作用力,与力F 平衡。
实际上内力是分布在整个横截面上的,N F 应为横截面上内力的合力,通常称N F 为截面m-n 上的内力,它的大小可由平衡方程求得,即0=∑X F0=-F FF F N =(二)直杆轴向拉伸及压缩的应力1.应力的定义单位面积上的内力称为应力。


.Word 资料机械设计基础(含工程力学)课程标准课程代码:课程性质:必修课课程类型:B类课(一)课程目标《工程力学》是机械设计与制造专业的一门重要的主干课程。
在整个教学过程中应从高职教育培养目标和学生的实际情况出发,在教学内容的深广度、教学方法上都应与培养高技能人才目标接轨。
通过本课程的学习,使学生达到以下目标:1、深刻理解力学的基本概念和基本定律,熟练掌握解决工程力学问题的定理和公式。
能将实际物体简化成准确的力学模型,应用力学基本概念和定理解决相关力学问题;2、能对静力学问题进行分析和计算,对刚体、物系进行受力分析和平衡计算;3、正确应用公式对受力不很复杂的构件进行强度、刚度和稳定性的计算;4、通过应力状态分析建立强度理论体系。
5、步掌握材料的力学性能及材料的相关力学实验。
掌握基本实验的操作及测试方法(二)课程内容与要求工程力学分为理论力学和材料力学部分。
理论力学部分以静力学为主,包括静力学基础、力系的简化、力系的平衡。
材料力学部分包括杆件的四种基本变形(轴向拉伸与压缩、剪切与挤压、扭转、弯曲)的内力、应力和变形,应力状态与强度理论,组合变形杆的强度和压杆稳定。
第一篇静力学静力学主要内容有:力的概念,约束与约束反力,受力分析和受力图;力对点的矩,力对轴的矩,力偶与力偶系的简化,力的平移,力系的简化;平衡条件与平衡方程,特殊力系的平衡,空间一般力系的平衡,物体系的平衡,平面静定桁架的内力,考虑摩擦时的平衡。
第二篇材料力学材料力学主要内容有:材料的力学性能,拉伸与压缩时的力学性能,构件的强度、刚度和稳定性,强度条件、刚度条件,应力状态分析与四种强度理论。
课程要求:熟练掌握静力学的基本概念:四个概念、六个公理及推论、一个定理。
能应用静力学的基本理论对刚体进行受力分析;明确平面任意力系的简化;熟练掌握平面力系的平衡方程及其应用;掌握材料力学的基本概念;掌握四种变形方式的内力、应力、内力图;学会四种载荷作用方式下强度、刚度、稳定性计算;理解应力状态与强度理论。



直杆轴向拉伸与压缩时的变形与应力分析和拉伸与压缩时材料的力学性能——教案第一章:直杆轴向拉伸与压缩的基本概念1.1 学习目标1. 了解直杆轴向拉伸与压缩的基本概念;2. 掌握直杆轴向拉伸与压缩的变形与应力分析方法。
1.2 教学内容1. 直杆轴向拉伸与压缩的定义;2. 直杆轴向拉伸与压缩的变形与应力分析方法。
1.3 教学活动1. 讲解直杆轴向拉伸与压缩的基本概念;2. 分析直杆轴向拉伸与压缩的变形与应力分析方法。
第二章:直杆轴向拉伸与压缩的变形分析2.1 学习目标1. 了解直杆轴向拉伸与压缩的变形规律;2. 掌握直杆轴向拉伸与压缩的变形分析方法。
2.2 教学内容1. 直杆轴向拉伸与压缩的变形规律;2. 直杆轴向拉伸与压缩的变形分析方法。
2.3 教学活动1. 讲解直杆轴向拉伸与压缩的变形规律;2. 分析直杆轴向拉伸与压缩的变形分析方法。
3.1 学习目标1. 了解直杆轴向拉伸与压缩的应力分布;2. 掌握直杆轴向拉伸与压缩的应力分析方法。
3.2 教学内容1. 直杆轴向拉伸与压缩的应力分布;2. 直杆轴向拉伸与压缩的应力分析方法。
3.3 教学活动1. 讲解直杆轴向拉伸与压缩的应力分布;2. 分析直杆轴向拉伸与压缩的应力分析方法。
第四章:拉伸与压缩时材料的力学性能4.1 学习目标1. 了解拉伸与压缩时材料的力学性能指标;2. 掌握拉伸与压缩时材料的力学性能分析方法。
4.2 教学内容1. 拉伸与压缩时材料的力学性能指标;2. 拉伸与压缩时材料的力学性能分析方法。
4.3 教学活动1. 讲解拉伸与压缩时材料的力学性能指标;2. 分析拉伸与压缩时材料的力学性能分析方法。
第五章:实例分析与应用5.1 学习目标2. 能够应用所学知识解决实际问题。
5.2 教学内容1. 直杆轴向拉伸与压缩的实例分析;2. 应用所学知识解决实际问题。
5.3 教学活动1. 分析直杆轴向拉伸与压缩的实例;2. 解决实际问题,巩固所学知识。
第六章:弹性模量的概念与应用6.1 学习目标1. 理解弹性模量的定义及其物理意义;2. 掌握弹性模量在材料力学中的应用。

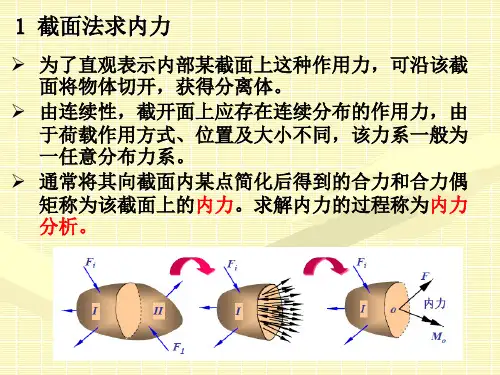
A=10mm 2
A=100mm 2
10KN 10KN
100KN 100KN
哪个杆先破坏?
§3
应力.拉(压)杆内的应力
应力的概念
受力杆件某截面上一点的内力分布疏密程度,内力集度.F 1
F n
F 3
F 2
应力就是单位面积上的力?
(工程构件,大多数情形下,内力并非均匀分布,集度的定义不仅准确而且重要,因为“破坏”或“失效”往往从内力集度最大处开始。
)
F 1
F 2
ΔA
D F
ΔF Qy
ΔF Qz
ΔF N
dA
dF A F N
N A =
D D =→D 0
lim σdA
dF A F Q
Q A =D D =→D 0
lim τ垂直于截面的应力称为“正应力”位于截面内的应力称为“切应力”
应力的国际单位为N/m 2 (帕斯卡)
1N/m 2=1Pa
1MPa=106Pa =1N/mm 21GPa=109Pa
dA
dF A
F p A =
D D =→D 0
lim
拉(压)杆横截面上的应力
A
dA dA F A
A
N σσσ===⎰⎰A
F N
=
σ几何变形
平面假设
静力平衡
dA
dF A F N
N A =D D =→D 0
lim σdA dF N σ=横截面上各点只产生沿垂直于横截面方向的变形
横截面上只有正应力
两横截面之间的纵向纤维伸长都相等
杆件的横截面在变形后仍保持为平面,且垂直于杆的轴线
横截面上的正应力均匀分布
σ——正应力F N ——轴力
A ——横截面面积
σ的符号与F N 轴力符号相同
A
F N
=
σ
试计算图示杆件1-1、2-2、和3-3截面上的正应力.已知横截面面积A=2×103mm 2
20KN
20KN
40KN 40KN
3
3
2
2
1
1
例题2.5
20kN
40kN
MPa
1011-=-σ0
22=-σMPa
2033=-σ
图示支架,AB 杆为圆截面杆,d=30mm ,BC 杆为正方形截面杆,其边长a=60mm ,F=10KN ,试求AB 杆和BC 杆横截面上的正应力。
例题2.6
F NAB
F NBC
MPa A F AB
NAB AB
3.28==σMPa A F BC
NBC BC
8.4-==σF
F NAB =0
30sin NBC
NAB F F -=0
30cos C
d
A
B F
a
30
试求图示结构AB 杆横截面上的正应力。
已
知F=30KN ,A=400mm
2F D
B
C
A
a
a
a
例题2.7
F NAB
2=⨯-⨯a F a F AB N F
F NAB 2=MPa
A
F NAB 150==σ
计算图示结构BC 和CD 杆横截面上的正应力值。
已知CD 杆为φ28的圆钢,BC 杆为φ22的圆钢。
20kN
18kN D
E
C
30
O
B
A 4m
4m 1m
例题
2.8
F NBC
以AB 杆为研究对像
0=∑A
m 05189=⨯-⨯NAB F kN F NBC 10=以CDE 为研究对像
F NCD
=∑E
m
4208830sin 0
=⨯-⨯-⨯NBC NCD F F kN
F NCD 40=BC NBC BC
A F =σCD
NCD CD
A F =σ
实验:
设一悬挂在墙上的弹簧秤,施加初拉力将其钩在不变形的凸缘上。
若在弹簧的下端施加砝码,当所加砝码小于初拉力时,弹簧秤的读数将保持不变;当所加砝码大于初拉力时,则下端的钩子与凸缘脱开,弹簧秤的读数将等于所加砝码的重量。
实际上,在所加砝码小于初拉力时,钩子与凸缘间的作用力将随所加砝码的重量而变化。
凸缘对钩子的反作用力与砝码重量之和,即等于弹簧秤所受的初拉力。
在一刚性板的孔中装置一螺栓,旋紧螺栓使其产生预拉力F 0,然后,在下面的螺母上施加外力F.假设螺栓始终处于弹性范围,且不考虑加力用的槽钢的变形.试分析加力过程中螺栓内力的变化.
F F ≤螺栓拉力0F F N =0
F F ≥螺栓拉力
F
F N =
(轴向脱离问题)左端固定的等直杆,长度和拉(压)刚度分别为l 和EA ,预拉伸长δ后,右端加一刚性支撑,然后,在杆的右端施加一轴向拉力F 。
设杆件始终在线弹性范围内工作,试分析外力F 的施加过程中杆件轴力F N 的变化。
预拉力
F
l
EA F δ=
0如果
l
EA F δ≤
则l EA F N δ
=
如果
l
EA F δ≥
则
F
F N =F
F N
l
EA δl
EA δ0
(轴向接触问题)左端固定的等直杆,长度和拉(压)刚度分别为l 和EA ,右端作用一轴向拉力F ,杆伸长δ后,右端与支撑刚性接触,然后,外力F 继续加大。
设杆件始终在线弹性范围内工作,试分析外力F 的施加过程中杆件轴力F N 的变化。
预拉力
l
EA F δ=
0如果l EA F δ≤则
l
EA F N δ=如果l
EA F δ≥则F
F N =F
F
F N
l
EA δl
EA δ0
书中例题
长为b 、内径d=200mm 、壁厚δ=5mm的薄壁圆环,承受p=2MPa 的内压力作用,如图a 所示。
试求圆环径向截面上的拉应力。
b
P
P
d
ϕϕπ
sin )2(0⎰⋅=d d pb F R 2
2pbd F F R N =
=A F N =σMPa Pa m m Pa 401040)
105(2)2.0)(102(636
=⨯=⨯⨯=-b
P
P
δ
d
N
F N
F y
m n
d
R F ϕ
d ϕ
n m ϕϕπ
d pbd ⎰=0sin 2
pbd
=δδ22pd b pbd ==
F
X
σα——斜截面上的正应力;τα——斜截面上的切应力
α
α
στ
n
α
τασααcos p =ααcos A F N =ασ2
cos =αασsin cos =α
τααsin p =α
σ2sin 2
1
=α
p F
F
拉(压)杆斜截面上的应力
αα
αA F N =α
α
cos A =
横截面----是指垂直杆轴线方向的截面;斜截面----是指任意方位的截面。
讨论:
轴向拉压杆件的最大正应力发生在横截面上。
轴向拉压杆件的最大切应力发生在与杆轴线成450截面上。
在平行于杆轴线的截面上σ、τ均为零。
1=α、σ
σ=max 0
452=α、σ
τ2
1max
=0
90
3=α、0
090=σ0
90=τα
σσα2
cos =α
στα2sin 2
1
=0
45-=ασ
τ21m in -=F
45
σ045τ0
45
-σ0
45
-τ切应力互等定理
A
F N
=
σ圣维南原理。