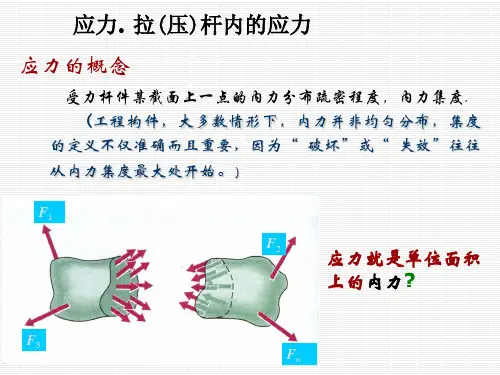
02.3.应力·拉(压)杆内的应力解析
- 格式：ppt
- 大小：2.78 MB
- 文档页数：24
下载文档原格式
合集下载
拉伸压缩与剪切拉压杆的内力及应力拉压杆的变形金属拉压时的力学性能许用应力及强条件圣维南原理与应力集中
2、基本实验
拉伸和压缩实验
a)
3、金属材料
塑性材料：低碳钢 b)
脆性材料：铸铁
4、拉伸试件
d
l
A
l 图 2-13
圆截面 矩形截面
l 10d 或
l 5d
l 11.3 A 或 l 5.65 A
第18页/共57页
§2.3 金属拉压时的力学性能
低碳钢拉伸时的力学性质
F
(1) 拉伸曲线 F l 曲线
10 kN
5 kN 5 kN
A
1m
C
D
B
0.5 m 0.5 m
FN1 10 kN , FN2 0 , FN3 5 kN
轴力图如图b所示
FN / kN
10
b)
(+
)
第14页/共57页
(-)
x
5
§2.2 拉压杆的变形
由胡克定律， 各段的轴向变形为
10 kN
5 kN 5 kN
a)
A
C
D
B
1m
0.5 m 0.5 m
沿杆轴线方向的坐标x表示横截面的位置，垂直于杆轴线的坐标代 表轴力FN的图线。
目的
用图线表示形象地表示轴力沿杆件轴线的变化情况，从而确定最大 轴力及其作用位置
第4页/共57页
§2.1 拉压杆的内力及应力
例2-1 图2-5a所示左端固定、右端自由的轴向受力杆件。试求1-1、2-2和3-3截面上 的轴力，并作轴力图。
52.0 106
Pa
52.0 MPa（压）
第8页/共57页
§2.1 拉压杆的内力及应力
拉压杆斜截面上的应力
假开想，地以将杆表沿示与该横斜截面面的成面角积的斜面Ak-k截 F
《材料力学》课件2-3应力.拉(压)杆内的应力
FNAB sin 300 F
d
A
FNAB cos 300 FNBC
FNAB
300
C
B
AB
FNAB 28.3MPa AAB
a
FNBC
F
BC
FNBC 4.8MPa ABC
例题 2.7
试求图示结构AB杆横截面上的正应力。已 知F=30KN，A=400mm2
F 2a FN AB a 0
应力.拉(压)杆内的应力 应力的概念
受力杆件某截面上一点的内力分布疏密程度，内力集度. (工程构件，大多数情形下，内力并非均匀分布，集度 的定义不仅准确而且重要，因为“ 破坏”或“ 失效”往往 从内力集度最大处开始。)
F1 F2
应力就是单位面积 上的内力?
F3
Fn
F1
ΔFQy
DF
ΔA
Δ FN
垂直于截面 的应力称为 “ 正应力”
45
F
0
1 杆轴线成450截面上。 min 2 450 45
0
1 轴向拉压杆件的最大切应力发生在与 2
45
45
切应力互等定理
0
0
3、 900
90 0
0
90 0
0
在平行于杆轴线的截面上σ、τ均为零。
FN A
圣维南原理
书中例题
长为b、内径d=200mm、壁厚δ=5mm的薄壁圆环， 承受p=2MPa的内压力作用，如图a所示。试求 圆环径向截面上的拉应力。
d
b
P
P
y
d
b
P
P
FR d
d
A
FNAB cos 300 FNBC
FNAB
300
C
B
AB
FNAB 28.3MPa AAB
a
FNBC
F
BC
FNBC 4.8MPa ABC
例题 2.7
试求图示结构AB杆横截面上的正应力。已 知F=30KN，A=400mm2
F 2a FN AB a 0
应力.拉(压)杆内的应力 应力的概念
受力杆件某截面上一点的内力分布疏密程度，内力集度. (工程构件，大多数情形下，内力并非均匀分布，集度 的定义不仅准确而且重要，因为“ 破坏”或“ 失效”往往 从内力集度最大处开始。)
F1 F2
应力就是单位面积 上的内力?
F3
Fn
F1
ΔFQy
DF
ΔA
Δ FN
垂直于截面 的应力称为 “ 正应力”
45
F
0
1 杆轴线成450截面上。 min 2 450 45
0
1 轴向拉压杆件的最大切应力发生在与 2
45
45
切应力互等定理
0
0
3、 900
90 0
0
90 0
0
在平行于杆轴线的截面上σ、τ均为零。
FN A
圣维南原理
书中例题
长为b、内径d=200mm、壁厚δ=5mm的薄壁圆环， 承受p=2MPa的内压力作用，如图a所示。试求 圆环径向截面上的拉应力。
d
b
P
P
y
d
b
P
P
FR d
轴向拉、压杆的内力及应力计算
解：（1）计算各段的轴力
AB段：用1-1截面在AB段内将杆截开，取左段为研究对象，以N1表示截面上的轴力，并假设为拉力。写出平
衡方程： ∑X=0，N1+P1=0
得 N1=-P1=-20KN 负号表示AB段轴力N1实际为压力。
BC段：同理写出平衡方程： ∑X=0，N2+P1-P2=0
得 N2=-P1+P2=-20+30=10KN 正号表示BC段轴力N2实际为拉力。
面垂直的应力为正应力，与截面相切的应力为剪应力。轴向拉伸、压缩时，杆件
截面上各点处产生正应力，且大小相等。若应力用σ表示，横截面积为A，轴力
为N，则
N
A
正应力的正负号规定：拉应力为正，压应力为负。
课题七 轴向拉、压杆的内力及应力计算
例：如图7-2a悬臂梁，已知P1=20KN，P2=30KN，P3=10KN，试画出杆的轴力图。
课题七 轴向拉、压杆的内力及应力计算
三、轴力图
表明沿杆长各横截面轴力变化规律的图形称为轴力图。用平行于杆轴线的坐 标表示横截面的位置，用垂直于杆轴线的坐标表示横截面上的轴力，按选定的比 例尺把正轴力画在轴的上方，负轴力画在轴的下方，并连成直线，就得到轴力 图。
四、轴向拉、压杆横截面上的应力
单位面积课题七 轴向拉、压杆的内力及应力计算
一、轴向拉伸和压缩
受力特点：直杆的两端沿杆轴线方向作用一对大小相等，方向相反的力。 变形特点：在外力作用下产生轴线方向的伸长或缩短。 当作用力背离杆端时，作用力是拉力，杆件产生伸长变形，叫做轴向拉伸。 见图7-1a 当作用力指向杆端时，作用力是压力，杆件产生压缩变形，叫做轴向压缩。 见图7-1b
图 7-1
课题七 轴向拉、压杆的内力及应力计算
AB段：用1-1截面在AB段内将杆截开，取左段为研究对象，以N1表示截面上的轴力，并假设为拉力。写出平
衡方程： ∑X=0，N1+P1=0
得 N1=-P1=-20KN 负号表示AB段轴力N1实际为压力。
BC段：同理写出平衡方程： ∑X=0，N2+P1-P2=0
得 N2=-P1+P2=-20+30=10KN 正号表示BC段轴力N2实际为拉力。
面垂直的应力为正应力，与截面相切的应力为剪应力。轴向拉伸、压缩时，杆件
截面上各点处产生正应力，且大小相等。若应力用σ表示，横截面积为A，轴力
为N，则
N
A
正应力的正负号规定：拉应力为正，压应力为负。
课题七 轴向拉、压杆的内力及应力计算
例：如图7-2a悬臂梁，已知P1=20KN，P2=30KN，P3=10KN，试画出杆的轴力图。
课题七 轴向拉、压杆的内力及应力计算
三、轴力图
表明沿杆长各横截面轴力变化规律的图形称为轴力图。用平行于杆轴线的坐 标表示横截面的位置，用垂直于杆轴线的坐标表示横截面上的轴力，按选定的比 例尺把正轴力画在轴的上方，负轴力画在轴的下方，并连成直线，就得到轴力 图。
四、轴向拉、压杆横截面上的应力
单位面积课题七 轴向拉、压杆的内力及应力计算
一、轴向拉伸和压缩
受力特点：直杆的两端沿杆轴线方向作用一对大小相等，方向相反的力。 变形特点：在外力作用下产生轴线方向的伸长或缩短。 当作用力背离杆端时，作用力是拉力，杆件产生伸长变形，叫做轴向拉伸。 见图7-1a 当作用力指向杆端时，作用力是压力，杆件产生压缩变形，叫做轴向压缩。 见图7-1b
图 7-1
课题七 轴向拉、压杆的内力及应力计算
材料力学讲义
第一章 绪论及基本概念§1−1 材料力学的任务要想使结构物或机械正常地工作，必须保证每一构件在荷载作用下能够安全、正常地工作。
因此，在力学上对构件有一定的要求：1． 强度，即材料或构件抵抗破坏的能力； 2． 刚度，即抵抗变性的能力；3． 稳定性，承受荷载时，构件在其原有形态下的平衡应保持为稳定平衡§1−2 可变性固体的性质及基本假设可变性固体：理学弹性体、小变性 基本假设：1． 连续、均匀性； 2． 各项同性假设。
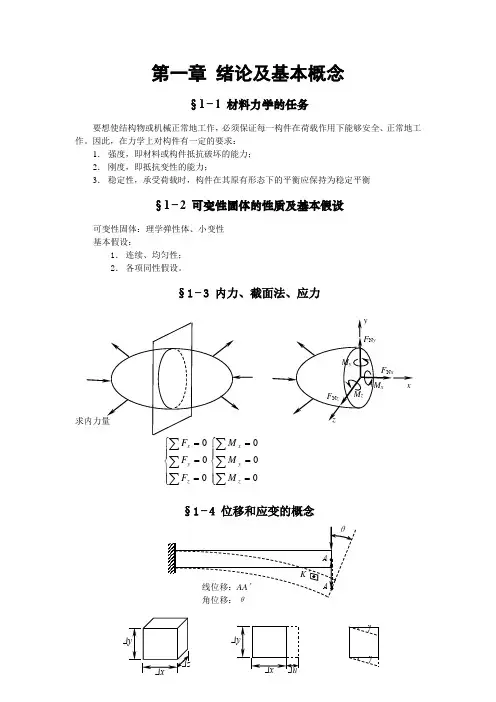
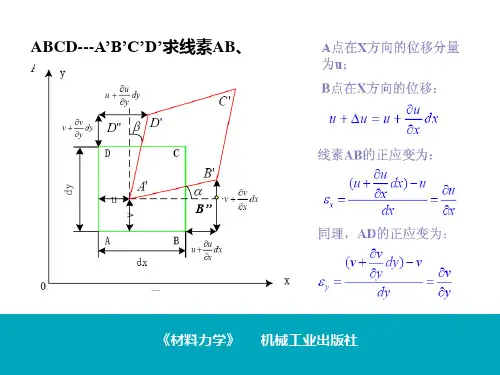
§1−3 内力、截面法、应力⎪⎪⎩⎪⎪⎨⎧===∑∑000z y x F F F ⎪⎪⎩⎪⎪⎨⎧===∑∑000z y xM M M§1−4 位移和应变的概念x u x x ∆∆=→∆0limε称为K 点处沿x 方向的线应变 直角的改变量γ称为切应变。
§1−5 杆件变性的基本形式1．轴向拉伸或轴向压缩2．剪切3．扭转4．弯曲第二章 轴向拉伸和压缩§2−1 轴向拉伸和压缩的概念F(图2−1)则为轴向拉伸，此时杆被2−1虚线)；若作用力F 压缩杆件(图(图2−2工程中许多构件，(图2−3)、各类(图2−4)等，这类结构的构2−1和图2−2。
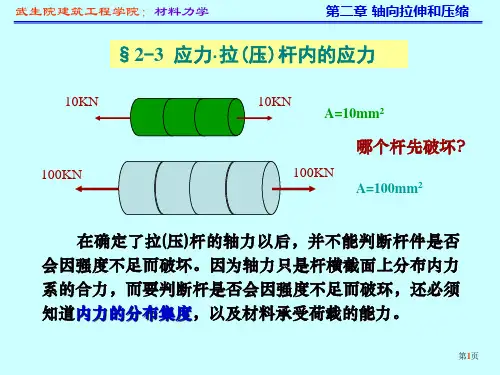
§ 2−2 内力·截面法·轴力及轴力图一、横截面上的内力——轴力图2−5a 所示的杆件求解横截面m−m 的内力。
按截面法求解步骤有：可在此截面处假想将杆截断，保留左部分或右部分为脱离体，移去部分对保留部分的作用，用内力来代替，其合力F N ，如图2−5b 或图2−5c 所示。
对于留下部分Ⅰ来说，截面m −m 上的内力F N 就成为外力。
由于原直杆处于平衡状态，故截开后各部分仍应维持平衡。
根据保留部分的平衡条件得 mF N F N （a ）（b ） （c ）图2−5Ⅱ图2−1图2−2图2-4F F F F Fx==-=∑N N ,0,0(2−1)式中，F N 为杆件任一截面m −m 上的内力，其作用线也与杆的轴线重合，即垂直于横截面并通过其形心，故称这种内力为轴力，用符号F N 表示。
轴向拉伸和压缩—轴向拉(压)杆的应力(建筑力学)
轴向拉伸与压缩
根据从杆件表面观察到的现象，从变形的可能性考虑， 可推断：
轴向拉杆在受力变形时，横截面只沿杆轴线平行移动。 由此可知：横截面上只有正应力σ。 假如把杆想象成是由许多纵向纤维组成的话，则任意两个 横截面之间所有纵向纤维的伸长量均相等，即两横截面间的变 形是均匀的，所以拉（压）杆在横截面上各点处的正应力σ都 相同。
500 500
0.72MPa
由结果可见，砖柱的最大工作应力在柱的下段，其值为 0.72MPa，是压应力。
轴向拉伸与压缩
第三节 轴向拉（压）杆的应力
变形规律试验：
FP
FP
观察发现：当杆受到轴向拉力作用后，所有的纵向线都 伸长了，而且伸长量都相等，并且仍然都与轴线平行；所有 的横向线仍然保持与纵向线垂直，而且仍为直线，只是它们 之间的相对距离增大了。
1
FN1 A1
28.3103
202
90MPa(拉应力)
4
2
FN 2 A2
20103 152
89MPa(压应力)
FP
FN
轴向拉伸与压缩
拉（压）杆横截面上任一点 处正应力的计算公式为
FN
A
式中， A为拉（压）杆横截面的面积；FN为轴力。
当FN为拉力，则σ为拉应力，拉应力为正； 当FN为压力，则σ为压应力，压应力为负。
通过上述分析知：轴心拉杆横截面上只有一分布的，所以拉杆横 截面上正应力的计算公式为
各段横截面上应力为
AB段：
AB
FNAB A
15 103 2500
MPa
6MPa
（压应力）
BC段： BC
FNBC A
8 103 2500
MPa
3.2MPa
材料力学第02章轴向拉应力详解
Page 30
《材料力学》 机械工业出版社
第二章 轴向拉应力与材料的力学性能
拉（压）杆应力
应力集中的程度用应力集中因数描述。应力集中 处横截面上的应力最大值与不考虑应力集中时的应力 值(称为名义应力)之比，称为应力集中因数(factor of stress concentration)，用k表示：
第二章 轴向拉应力与材料的力学性能
4) 特征应力
重要概念： 比例极限——应力应变线性 弹性极限——应力应变弹性 ✓ 弹性：卸载后完全恢复
线性一定是弹性 弹性不一定线性！
《材料力学》 机械工业出版社
比例极限σp 弹性极限σe 屈服极限σs 强度极限σb
Page 46
第二章 轴向拉应力与材料的力学性能 5)卸载定律
《材料力学》 机械工业出版社
截面法步骤—— 截，取，代，平
∑Fx = 0 , FN－F = 0
∴ FN = F
取左半和取右 半计算内力， 结果是一样的。
Page 15
《材料力学》 机械工业出版社
第二章 轴向拉应力与材料的力学性能
轴力与轴力图
二、 轴力图
纵轴表示轴力大小的图（横轴为截面位置）。
方法：画几何图， 横坐标——杆的轴线； 纵坐标——轴力。
目标：弄清楚截面方向对应力的影响。
《材料力学》 机械工业出版社
研究方法） 平衡思想
Page 33
四、 斜截面上的应力
A
Aa
PP
k
面积: A
横截面
正应力: s =P/A
斜截面 面积：Aa =A/cosa 内力：Pa= P,
k
斜截面 全应力 p = P /A = Pcos / A = scos
02.3.应力·拉(压)杆内的应力解析
4
FF
90106 Pa 90MPa
x
s2
FN 2 A2
20103 152 106
FN1 28.38k9N106 PaFN289M20PkaN
第19页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
Ⅲ. 拉(压)杆斜截面上的应力
k
F
F
k
k
F
F
斜截面上的内力： F F
k
变形假设：两平行的斜截面在杆受拉(压)而变形后仍相 互平行。
第二章 轴向拉伸和压缩
平均应力的定义
受力杆件(物体)某一截面的M点附近微面积ΔA上分布 内力的平均集度即平均应力， p F ，其方向和大小一般
m A
随所取ΔA的大小而不同。
F
M
A
第3页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
总应力定义：
该截面上M点处分布内力的集度为
p
lim F
A0 A
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
ac
F
a
c
F
b
d
bd
3. 推论：拉(压)杆受力后任意两个横截面之间纵向线段 的伸长(缩短)变形是均匀的。由于假设材料是均匀的，而杆 的分布内力集度又与杆件纵向线段的变形相对应，因而杆件
横截面上的正应力s呈均匀分布，亦即横截面上各点处的正 应力s 都相等。由合力概念知：
第15页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
例题2-3 已知薄壁圆环 d = 200 mm，δ= 5 mm，p = 2 MPa。试求薄壁圆环在内压力作用下径向截面上的拉应力。
拉压杆应力、变形分析
通过这些数学模型，可以计算出在给定外力作用下物体的应 力和变形，从而对物体的力学性能进行评估。
应力与变形的实验验证
为了验证应力与变形的数学模型的正确性和可靠性，需要 进行实验验证。
实验中，可以通过测量物体的应力和变形数据，与数学模 型计算结果进行对比，以评估模型的准确性和适用范围。
05 拉压杆的优化设计
实验结果表明，拉压杆的应力分布不均匀，呈现 中间大、两端小的趋势。变形则表现为杆件中部 向下弯曲，两端向上翘起。
本研究采用有限元分析方法对拉压杆进行应力、 变形分析，得到了与实验结果较为一致的分析结 果，验证了有限元方法的可行性和有效性。
研究展望
虽然本研究取得了一定的成 果，但仍有许多问题需要进 一步探讨。例如，可以考虑 研究不同材料属性、不同截 面形状和不同边界条件等因 素对拉压杆应力、变形的影 响。
基于应力的优化设计
总结词
在基于应力的优化设计中，主要目标 是减小拉压杆的最大应力值，使其不 超过材料的许用应力。
详细描述
通过调整拉压杆的截面尺寸、长度、 材料等参数，可以改变其应力分布和 大小。常用的方法包括有限元分析和 数学优化算法。
基于变形的优化设计
总结词
基于变形的优化设计旨在减小拉压杆 的最大变形量，以确保其在工作过程 中具有良好的性能和精度。
根据应力的性质，可分为 拉应力和压应力；根据应 力的分布，可分为均匀应 力和非均匀应力。
应力状态
描述杆件内部各点的应力 状态，包括正应力和剪应 力。
拉压杆应力计算
轴向拉压杆
通过材料力学中的胡克定律计算拉压 杆的应力。
弯曲梁
扭转变形
利用扭矩和剪切模量计算扭转变形的 应力。
利用弯矩和剪力计算弯曲梁的应力。
拉压杆的应力
p
FN Aα
F cos
A
——横截面上的正应力。
cos
p称为斜截面上的全应力，可将它沿截面的法向和切向分解为
两个分量：正应力和切应力(如图)。它们分别为
目录
轴向拉伸和压缩\拉压杆的应力
pαcos cos2
pα
sin
cos
sin
2
sin
2
这就是拉压杆斜截面上应力的计算公式。
由公式可知，在通过拉压杆内任一点的各个截面上，一般都存
MPa
3 4
75 MPa
30
2
cos230
1 0 0MP a 2
3 43.2MPa 2
＝30 斜截面(如图)中的斜截面2－2上的正应力和切应力分别为
30
cos 2 30 100
MPa
3 4
75 MPa
30
2
cos2 30
10
0MP 2
a
3 2
43.2
MP
a
目录
轴向拉伸和压缩\拉压杆的应力 将上面求得的应力分别表示在它们所作用的截面上，如图b、c
目录
轴向拉伸和压缩\拉压杆的应力 【例2.2】图示一悬臂吊车的简图，斜杆BC的横截面面积A＝
500 mm，荷载F＝25 kN。试求当荷载F移至D点时，斜杆横截面上 的正应力。
目录
轴向拉伸和压缩\拉压杆的应力
【解】 悬臂吊车的计算简图如图b所示。 为了求出斜杆BC的轴向外力FBC，取横梁AD为研究对象。
列出平衡方程
∑MA＝0， FBC sin45×1.5m－F×3m＝0
得
F 3m
25 kN 3m
FBC sin45 1.5m 0.707 1.5m 70.7 kN
《材料力学》课件2-3应力.拉(压)杆内的应力
施加预压力
在拉(压)杆上施加一定的预压 力，以消除实验误差。
数据处理
根据实验数据计算杆内部的应 力分布。
实验结果与讨论
01
实验结果
通过实验测量得到拉(压)杆内部 的应力分布情况，与理论值进行 对比。
结果分析
02
03
结果讨论
分析实验结果与理论值的差异， 探讨可能的影响因素，如实验误 差、材料性质等。
强度条件
拉(压)杆的强度条件是指杆件在 承受外力时不发生屈服、断裂 或严重变形的条件。
弹性极限
在弹性范围内，拉(压)杆的应力 与应变呈线性关系，当应力达 到弹性极限时，杆件发生屈服 。
屈服极限
当拉(压)杆的应力超过弹性极限 后，杆件进入屈服阶段，此时 应力不再增加，但变形继续增 大。
强度极限
拉(压)杆的强度极限是指杆件所 能承受的最大应力值，超过这 个极限值，杆件会发生断裂。
应力的表示方法
总结词
应力的表示方法包括符号表示、单位表示和公式表示等。
详细描述
在材料力学中，应力的表示方法包括符号表示、单位表示和公式表示等。符号表示通常用希腊字母或英文字母表 示，如σ表示正应力，τ表示剪应力。单位表示则采用国际单位制中的牛顿或帕斯卡等单位。公式表示则是通过数 学公式来描述应力的分布和大小，如胡克定律等。
拉(压)杆内的应力是材料力学中的一个 基础知识点，对于理解材料的受力性 能和稳定性具有重要意义。
学习目标
掌握拉(压)杆内的应 力计算方法。
能够运用所学知识解 决实际工程中的拉 (压)杆问题。
理解拉(压)杆在不同 受力情况下的应力分 布规律。
02
材料力学的基本概念
应力的定义
总结词
应力的定义是指物体受到外力作用时， 单位面积上所 Nhomakorabea受的内力。
第3节 拉压杆的应力
第四章
轴向拉伸和压缩
第三节
一、应力的概念
拉压杆的应力
两根相同材料做成的粗细不同的直杆在相同拉 力作用下，用截面法求得的两杆横截面上的轴力是 相同的。若逐渐将拉力增大，则细杆先被拉断。这 说明杆的强度不仅与内力有关，还与内力在截面上 各点的分布集度有关。当粗细二根杆轴力相同时， 细杆内力分布的密集程度较粗杆要大一些，可见， 内力的密集程度才是影响强度的主要原因。为此我 们引入应力的概念。
AB段 （ห้องสมุดไป่ตู้）确定应力
1
2
AB段
FN1 1 80MPa A1
FN 2 BC段 2 83.3MPa A2
第四章
轴向拉伸和压缩
二、轴向拉压杆横截面上的应力
平面假设：杆变形后各横截面仍保持为平面，这个 假设称为平面截面假设。
第四章
轴向拉伸和压缩
正应力：横截面上应力的方向垂直于横截面，称为 “正应力”并以“ ”表示： 正应力
FN A
说明
式中 为横截面上的正应力，FN为横截面上的轴力， A为横截面面积。 当轴力为正时， 为拉应力取正号；当轴力为负时， 为压应力，取负号。 （1Pa=1N/m2） kPa、 、 应力的国际单位为Pa MPa、 GPa：
1kPa 10 Pa 1MPa 10 Pa 1GPa 10 Pa
3 6 9
第四章
轴向拉伸和压缩
例4-2 一阶梯杆如图所示，AB段横截面面积为： A1=100mm2，BC段横截面面积为A2=180mm2，试求： 各段杆横截面上的正应力。 解（1） 计算各段内 轴力，并绘制轴力图
1 2
FN1 8kN BC段 F 15kN N2
轴向拉伸和压缩
第三节
一、应力的概念
拉压杆的应力
两根相同材料做成的粗细不同的直杆在相同拉 力作用下，用截面法求得的两杆横截面上的轴力是 相同的。若逐渐将拉力增大，则细杆先被拉断。这 说明杆的强度不仅与内力有关，还与内力在截面上 各点的分布集度有关。当粗细二根杆轴力相同时， 细杆内力分布的密集程度较粗杆要大一些，可见， 内力的密集程度才是影响强度的主要原因。为此我 们引入应力的概念。
AB段 （ห้องสมุดไป่ตู้）确定应力
1
2
AB段
FN1 1 80MPa A1
FN 2 BC段 2 83.3MPa A2
第四章
轴向拉伸和压缩
二、轴向拉压杆横截面上的应力
平面假设：杆变形后各横截面仍保持为平面，这个 假设称为平面截面假设。
第四章
轴向拉伸和压缩
正应力：横截面上应力的方向垂直于横截面，称为 “正应力”并以“ ”表示： 正应力
FN A
说明
式中 为横截面上的正应力，FN为横截面上的轴力， A为横截面面积。 当轴力为正时， 为拉应力取正号；当轴力为负时， 为压应力，取负号。 （1Pa=1N/m2） kPa、 、 应力的国际单位为Pa MPa、 GPa：
1kPa 10 Pa 1MPa 10 Pa 1GPa 10 Pa
3 6 9
第四章
轴向拉伸和压缩
例4-2 一阶梯杆如图所示，AB段横截面面积为： A1=100mm2，BC段横截面面积为A2=180mm2，试求： 各段杆横截面上的正应力。 解（1） 计算各段内 轴力，并绘制轴力图
1 2
FN1 8kN BC段 F 15kN N2
杆件轴向拉伸或压缩时横截面上的内力和应力
CB为15×15的方截面杆。（不考虑重力，是二力 杆件）
解：1、计算各杆件的轴力。（设斜杆为1杆，水 平杆为2杆。力的指向可先假定一方向）
B 用截面法取节点B为研究对象
C
2
F
FN1
y
FN 2 45° B x
Fx 0 Fy 0
FN1 cos 45 FN 2 0 FN1 sin 45 F 0
§2.2 轴向拉伸或压缩时横截面上的内力和应力
二、截面法求内力
m F
m
F
FN
FN
Fx 0
FN F 0 FN F
(1)假想沿m-m横截面将杆切开
F
(2)留下左半段或右半段
(3)将弃去部分对留下部分的作
F 用用内力代替
(4)对留下部分写平衡方程 求出内力即轴力的值
§2.2 轴向拉伸或压缩时横截面上的内力和应力
§2.2 轴向拉伸或压缩时横截面上的内力和应力
FN
A
该式为横截面上的正应力σ计
算公式。正应力σ和轴力FN同号。 即拉应力为正，压应力为负。
圣 维 南 原 理
§2.2 轴向拉伸或压缩时横截面上的内力和应力
例题2.2
A
1
45°
图示结构，试求杆件AB、CB的应力。已知
F=20kN；斜杆AB为直径20mm的圆截面杆，水平杆
实验表明：拉（压）杆的破坏并不总是沿横截
面发生，有时却是沿斜截面发生的。
k
F
k
ห้องสมุดไป่ตู้
F FN F
AA
F
k p
F
F F
A
A
cos
F
k
k p
p
F A
F A
解：1、计算各杆件的轴力。（设斜杆为1杆，水 平杆为2杆。力的指向可先假定一方向）
B 用截面法取节点B为研究对象
C
2
F
FN1
y
FN 2 45° B x
Fx 0 Fy 0
FN1 cos 45 FN 2 0 FN1 sin 45 F 0
§2.2 轴向拉伸或压缩时横截面上的内力和应力
二、截面法求内力
m F
m
F
FN
FN
Fx 0
FN F 0 FN F
(1)假想沿m-m横截面将杆切开
F
(2)留下左半段或右半段
(3)将弃去部分对留下部分的作
F 用用内力代替
(4)对留下部分写平衡方程 求出内力即轴力的值
§2.2 轴向拉伸或压缩时横截面上的内力和应力
§2.2 轴向拉伸或压缩时横截面上的内力和应力
FN
A
该式为横截面上的正应力σ计
算公式。正应力σ和轴力FN同号。 即拉应力为正，压应力为负。
圣 维 南 原 理
§2.2 轴向拉伸或压缩时横截面上的内力和应力
例题2.2
A
1
45°
图示结构，试求杆件AB、CB的应力。已知
F=20kN；斜杆AB为直径20mm的圆截面杆，水平杆
实验表明：拉（压）杆的破坏并不总是沿横截
面发生，有时却是沿斜截面发生的。
k
F
k
ห้องสมุดไป่ตู้
F FN F
AA
F
k p
F
F F
A
A
cos
F
k
k p
p
F A
F A
【材料力学】孙训方第五版2-3
单元体的性质—平行面上，应力相等；
M
P
3、拉压杆内一点M 的应力单元体:
2012-6-4Leabharlann 14
4、拉压杆斜截面上的应力
取分离体如图3， a 逆时针为正；
a 绕研究对象顺时针转为正；
由分离体平衡得：
a a
0 0
cos a
2
a
a
x
sin a cos a
(1 cos 2a ) sin 2a
4
1 2 7 .4 M P a
max 0 / 2 127 . 4 / 2 63 . 7 MPa
a
a
2012-6-4
0
2
(1 cos 2a )
127 . 4 2
(1 cos 60 ) 95 . 5 MPa
0
2
sin 2a
127 . 4 2
sin 60 55 . 2 M Pa
6
3. 公式的应用条件： 等截面直杆、截面到载荷作用点有一定的距离。 不能适用于杆件两端外力作用区截面上各点的应力计算。 4. Saint-Venant原理： 离开载荷作用处一定距离（约为横截面尺寸），应力分布
与大小不受外载荷作用方式的影响。
2012-6-4
7
Saint-Venant原理与应力集中示意图 变形示意图： P a b c P
§2-3 应力· 拉(压)杆内的应力
一 应力的概念
1. 定义：由外力引起的内力集度 工程构件，大多数情形下，内力并非均匀分布，集度
的定义不仅准确而且重要，因为“破坏”或“失效”往
往从内力集度最大处开始。
6拉压内力和应力
力学精讲》，p15)。
9
10
图示结构， A、B、C为铰链连接，
A
求杆件AB、CB的应力。已知
F=20kN；AB为直径20mm的圆截面杆，
1 CB为15mm×15mm的方截面杆。
45° B
C
2F
FN1
y
FN 2 45° B x
F
解：1、计算各杆件的轴力。用 截面法取节点B为研究对象
Fx 0 Fy 0
向力FN后用式
s FN 求拉应力。 b
FN
FR 2
而
FR
π
( pb
d
d )s in
pbd
0
2
所以
s 1 ( pbd ) pd (2106 Pa)(0.2m)
b 2 2
2(510-3 m)
40106 Pa 40 MPa
14
§6-2 拉压杆的变形 胡克定律
纵向变形 ： 基本情况下(等直杆，两端受轴向力)：
34
FN1
FN 2 α
y Ax
F
2、根据斜杆的强度，求许可载荷
查表得斜杆AC的面积为 A1=2×4.8cm2
FN1 s A1
F1
1 2
s
A1
1 2
120 106
2
4.8 104
57.6103 N 57.6kN
35
FN1
FN 2 α
3、根据水平杆的强度，求许可载荷
y Ax
F
查表得水平杆AB的面积为 A2=2×12.74cm2
29
F=1000kN，b=25mm，h=90mm，α=200 。
〔σ〕=120MPa。试校核斜杆的强度。
F
第2讲 拉压杆的内力和应力
第2讲教学方案——拉压杆的内力和应力第二章轴向拉伸与压缩§2-1轴向拉伸与压缩的概念与实例轴向拉伸和压缩的杆件在生产实际中经常遇到，虽然杆件的外形各有差异，加载方式也不同，但一般对受轴向拉伸与压缩的杆件的形状和受力情况进行简化，计算简图如图2-1。
轴向拉伸是在轴向力作用下，杆件产生伸长变形，也简称拉伸；轴向压缩是在轴向力作用下，杆件产生缩短变形，也简称压缩。
实例如图2-2所示用于连接的螺栓；如图2-3所示桁架中的拉杆；如图2-4所示汽车式起重机的支腿；如图2-5所示巷道支护的立柱。
通过上述实例得知轴向拉伸和压缩具有如下特点：1. 受力特点：作用于杆件两端的外力大小相等，方向相反，作用线与杆件轴线重合，即称轴向力。
2. 变形特点：杆件变形是沿轴线方向的伸长或缩短。
§2-2横截面上的内力和应力1．内力在图2-6所示受轴向拉力P 的杆件上作任一横截面m —m ，取左段部分，并以内力的合力N代替右段对左段的作用力。
由平衡条件0=∑X ，得0=-P N由于0>P （拉力），则0>=P N合力N 的方向正确。
因而当外力沿着杆件的轴线作用时，杆件截面上只有一个与轴线重合的内力分量，该内力（分量）称为轴力，一般用N 表示。
若取右段部分，同理0=∑X ，知0=N -P得0>=P N图中N 的方向也是正确的。
材料力学中轴力的符号是由杆件的变形决定，而不是由平衡坐标方程决定。
习惯上将轴力N 的正负号规定为：拉伸时，轴力N 为正；压缩时，轴力N 为负。
2．轴力图轴力图可用图线表示轴力沿轴线变化的情况。
该图一般以杆轴线为横坐标表示截面位置，纵轴表示轴力大小。
例2-1 求如图2-7所示杆件的内力，并作轴力图。
解：（1）计算各段内力AC 段：作截面1—1，取左段部分（图b ）。
由0=∑X 得51=N kN （拉力）CB 段：作截面2-2，取左缎部分（图），并假设2N 方向如图所示。
由∑=0X 得KN N 102-=（2）绘轴力图选截面位置为横坐标；相应截面上的轴力为纵坐标，根据适当比例，绘出图线。
模块二-压杆的内力与应力
压杆的内力与应力
常用连接件的剪切面、挤压面的计算
A＝bl Ajy＝lh/2
冲压件
键连接
A πdt 1 Ajy πd 2 4
铆钉连接、销连接
1 A D 2 4 A jy dt
压杆的内力与应力
例1：图示装置常用来确定胶接处的抗剪强度， 如已知破坏时的荷载为10kN，试求胶接处的极 限剪（切）应力。
注意：截面不可取在力的作用点处
不能完全体现外力引起的变形效应
轴力讨论
X 0
选取截面顺序 从左至右 先求支座反力
从右至左 避开支座反力
局部平衡：
X 0
由截面法总结出规律： 数值：轴力的数值等于截面一侧所有外力的代数和
轴力图
例题 直杆AD受力如图所示。已知F1=16kN， 表示轴力沿杆轴变化情况的图线 F =10kN， F =20kN，试求出直杆AD的轴力图。 2 3 （即 FN-x 图 ）, 称为轴力图 基本步骤 选取截面 求出内力 画轴力图 轴力图意义
F
F＜Fcr 压杆的稳定性 力学模型
F＜Fcr
F＜Fcr
1.轴线为直线
2.压力作用线与轴线重合 3.均质等直杆件
干扰力
理想压杆 1.初曲率 2.压力作用线的偏离 3.材料不完全均匀 横 向 干 扰 力
(a)
(b)
(c)
当F＜Fcr时，撤去横向干扰力后，压杆仍能恢复原 有的直线平衡状态。 原有的直线平衡状态是稳定的。
胡克定律：在材料的弹性范围内，Δl与外力和杆长成正比， 与横截面面积成反比 弹性模量E 单位：Mpa, Gpa 获取方式：试验查表 意义：衡量材料抵抗 变形能力的指标，仅 与材料性质有关
试验表明，在弹性范围内
-直杆轴向拉伸与压缩时的应力分析
截面上的内力为 轴力——与轴线 重合
轴力
2．内力的计算——截面法
截面法计算内力
FN=F（合力FN 的方向与图示方向相同） 取杆件的一部分作为研究对象，利用静力平衡方程求 内力的方法称为截面法。
截面法计算内力
截面法求内力的三个步骤为：截开→代替→平衡。
关于轴力的正负有以下规定：当轴力的指向离开 截面时，杆受拉，规定轴力
三、变形与应变
拉杆
压杆
为了消除杆件长度的影响，通常以绝对变形除以原长得到单 位长度上的变形量——线应变（相对变形）来度量杆件的变形程
度，用符号ε表示 ：
ε =Δ L/Lo=（Lu-Lo）/Lo
式中，ε无单位，通常用百分数表示。对于拉杆，ε为正值； 对于压杆，ε为负值。
变形与应变
胡克定律：当杆件横截面上的正应力不超过 一定限度时， 杆的正应力σ与轴向线应变ε成正比。 即：
如图所示，两根材料一样、横截面面积不同的杆件，所 受外力相同，想一想，随着外力的增大，哪一根杆件先断？
不同横截面杆件受力
二、应力
工程上常用应力来衡量构件受力的强弱程度。
应力——构件在外力作用下，单位面积上的内力。某个 截面上，与该截面垂直的应力称为正应力，与该截面相切的 应力称为切应力。
由于拉伸或压缩时内力与横截面垂直，故其应力为正应 力（σ），应力单位：兆帕（MPa）。
σ =εE
常数E——材料的弹性模量，是衡量材料抵抗 弹性变形能力的一个指标。材料的E值越大，变形 越小。
1 Pa=1 N/m2，1 MPa=1 N/mm2 1 GPa（吉帕）=103 MPa=106 kPa=109 Pa
正应力计算公式：
σ FN A
式中 σ ——杆件横截面上的正应力，Pa； FN——杆件横截面上的轴力，N； A——杆件横截面面积，m2。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第8页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
F
a b
a
b
c
d
c d
F
3. 推论：拉(压)杆受力后任意两个横截面之间纵向线段 的伸长(缩短)变形是均匀的。由于假设材料是均匀的，而杆 的分布内力集度又与杆件纵向线段的变形相对应，因而杆件 横截面上的正应力s呈均匀分布，亦即横截面上各点处的正 应力s 都相等。由合力概念知：
第12页
武生院建筑工程学院：材料力学
• 讨论题
第13页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
例题2-2 试求此正方 形砖柱由于荷载引起的横 截面上的最大工作应力。 已知F = 50 kN。
第14页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
解：Ⅰ段柱横截面上的正应力
FN1 50 103 N s1 A1 (0.24 m) (0.24 m) 0.87 106 P a 0.87 MP a (压应力)
Ⅱ.轴向拉(压)杆横截面上的应力
(1) 与轴力相应的只可能是正应力s，与切应力无关； (2) s在横截面上的变化规律：横截面上各点处s 相等 时，可组成通过横截面形心的法向分布内力的合力——轴 力FN；横截面上各点处s 不相等时，特定条件下也可组成 轴力FN。
第7页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
Ⅱ段柱横截面上的正应力
FN 2 150103 N s2 0.37 m 0.37 m A2 1.1106 Pa 1.1 MPa (压应力)
s 2 s1
所以，最大工作应力为 smax= s2= -1.1 MPa (压应力）
第15页
武生院建筑工程学院：材料力学
第5页
武生院建筑工程学院：材料力学
正应力和切应力的正负规定： 1、对正应力s ：离开截面的正应力s 为正； 指向截面的正应力为负。 2、对切应力t：对截面内部一点产生顺时针力矩为正；
对截面内部一点产生逆时针力矩为负。
s （＋）
t
（＋）
s（－）
t （－）
第6页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
第1页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
Ⅰ.应力的概念
应力:指受力杆件某截面上某一点处的内力分布疏密 程度，即内力的分布集度。
（大多数情形下，工程构件的内力并非均匀分布，集 度的定义不仅准确而且重要，因为“ 破坏”或“ 失效” 往往从内力集度最大处开始。）
F1
F2
F3
Fn
第2页
武生院建筑工程学院：材料力学
F
实验现象及假设：
a b
a
b
c
d
c d
F
1. 观察等直杆表面上相邻两条横向线ab和cd在杆受拉 (压)后的相对位移：两横向线平移后仍为直线，仍相互平 行，且仍垂直于杆的轴线。 2. 设想横向线代表杆的横截面。平面假设——原为 平面的横截面在杆变形后仍为平面，对于拉(压)杆且仍相 互平行，仍垂直于轴线。
而
d FR ( pb d )sin pbd 0 2
π
所以
1 pbd pd (2 106 Pa)(0.2m) s ( ) b 2 2 2(510-3 m) 40106 Pa 40 MPa
FN A
第9页
得：等截面拉(压)杆横截面上正应力的计算公式 s
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
公式应用范围：
1. 上述正应力计算公式来自于平截面假设；对于某些 特定杆件,例如锲[qiè]形变截面杆受拉伸(压缩)时，平截面 假设不成立，故原则上不宜用上式计算其横截面上的正应力。
第二章 轴向拉伸和压缩
例题2-3 已知薄壁圆环 d = 200 mm，δ= 5 mm，p = 2 MPa。试求薄壁圆环在内压力作用下径向截面上的拉应力。
第16页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
解：薄壁圆环 (δ<<d )在内压力作用下，径向截面上的 拉应力可认为沿壁厚均匀分布，故在求出径向截面上的法 FN s 向力FN后,用式 求拉应力。 b F FN R 2
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
§2-3 应力· 拉(压)杆内的应力
10KN 10KN
A=10mm2
哪个杆先破坏?
100KN 100KN
A=100mm2
在确定了拉(压)杆的轴力以后，并不能判断杆件是否 会因强度不足而破坏。因为轴力只是杆横截面上分布内力 系的合力，而要判断杆是否会因强度不足而破环，还必须 知道内力的分布集度，以及材料承受荷载的能力。
A0
F dF ，其 A dA
方向一般既不与截面垂直，也不与截面相切，称为总应力。
F
M
A
p
M
第4页
武生院建筑工程学院：材料力学
p
t
M 某一截面上法向分 法向分量 正应力s 布内力在某一点处 的集度
s
总应力 p 切向分量 切应力t
某一截面上切向分 布内力在某一点处 的集度
应力单位：Pa(1 Pa = 1 N/m2，1 MPa = 106 Pa)。
第二章 轴向拉伸和压缩
平均应力的定义
受力杆件(物体)某一截面的M点附近微面积ΔA上分布 内力的平均集度即平均应力， p
m
F ，其方向和大小一般 A
随所取ΔA的大小而不同。
F
M
A
第3页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
总应力定义：
该截面上M点处分布内力的集度为 p lim
圣维南原理已被实验所证实，故等直拉压杆的正应 力计算都可以以公式 s FN 为准。 A
第11页
武生院建筑工程学院：材料力学
3、最大正应力： 等直杆受几个轴向外力时，由轴力图可求得其最大轴
FN 力 FN ,max ，代入公式 s 可得杆内最大正应力为： A
最大轴力所在的横截面成为危险截面，危险截面上的 正应力为最大工作应力。
2. 即使是等直杆，在外力作用点附近，横截面上的应 力情况复杂，实际上也不能应用上述公式。 圣维南(Saint-Venant)原理：“力作用于杆端方式的不同， 只会使与杆端距离不大于杆的横向尺寸的范围内受到影响”。
第10页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
圣维南(Saint-Venant)原理：“力作用于杆端方式的不同， 只会使与杆端距离不大于杆的横向尺寸的范围内受到影响”。
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
F
a b
a
b
c
d
c d
F
3. 推论：拉(压)杆受力后任意两个横截面之间纵向线段 的伸长(缩短)变形是均匀的。由于假设材料是均匀的，而杆 的分布内力集度又与杆件纵向线段的变形相对应，因而杆件 横截面上的正应力s呈均匀分布，亦即横截面上各点处的正 应力s 都相等。由合力概念知：
第12页
武生院建筑工程学院：材料力学
• 讨论题
第13页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
例题2-2 试求此正方 形砖柱由于荷载引起的横 截面上的最大工作应力。 已知F = 50 kN。
第14页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
解：Ⅰ段柱横截面上的正应力
FN1 50 103 N s1 A1 (0.24 m) (0.24 m) 0.87 106 P a 0.87 MP a (压应力)
Ⅱ.轴向拉(压)杆横截面上的应力
(1) 与轴力相应的只可能是正应力s，与切应力无关； (2) s在横截面上的变化规律：横截面上各点处s 相等 时，可组成通过横截面形心的法向分布内力的合力——轴 力FN；横截面上各点处s 不相等时，特定条件下也可组成 轴力FN。
第7页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
Ⅱ段柱横截面上的正应力
FN 2 150103 N s2 0.37 m 0.37 m A2 1.1106 Pa 1.1 MPa (压应力)
s 2 s1
所以，最大工作应力为 smax= s2= -1.1 MPa (压应力）
第15页
武生院建筑工程学院：材料力学
第5页
武生院建筑工程学院：材料力学
正应力和切应力的正负规定： 1、对正应力s ：离开截面的正应力s 为正； 指向截面的正应力为负。 2、对切应力t：对截面内部一点产生顺时针力矩为正；
对截面内部一点产生逆时针力矩为负。
s （＋）
t
（＋）
s（－）
t （－）
第6页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
第1页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
Ⅰ.应力的概念
应力:指受力杆件某截面上某一点处的内力分布疏密 程度，即内力的分布集度。
（大多数情形下，工程构件的内力并非均匀分布，集 度的定义不仅准确而且重要，因为“ 破坏”或“ 失效” 往往从内力集度最大处开始。）
F1
F2
F3
Fn
第2页
武生院建筑工程学院：材料力学
F
实验现象及假设：
a b
a
b
c
d
c d
F
1. 观察等直杆表面上相邻两条横向线ab和cd在杆受拉 (压)后的相对位移：两横向线平移后仍为直线，仍相互平 行，且仍垂直于杆的轴线。 2. 设想横向线代表杆的横截面。平面假设——原为 平面的横截面在杆变形后仍为平面，对于拉(压)杆且仍相 互平行，仍垂直于轴线。
而
d FR ( pb d )sin pbd 0 2
π
所以
1 pbd pd (2 106 Pa)(0.2m) s ( ) b 2 2 2(510-3 m) 40106 Pa 40 MPa
FN A
第9页
得：等截面拉(压)杆横截面上正应力的计算公式 s
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
公式应用范围：
1. 上述正应力计算公式来自于平截面假设；对于某些 特定杆件,例如锲[qiè]形变截面杆受拉伸(压缩)时，平截面 假设不成立，故原则上不宜用上式计算其横截面上的正应力。
第二章 轴向拉伸和压缩
例题2-3 已知薄壁圆环 d = 200 mm，δ= 5 mm，p = 2 MPa。试求薄壁圆环在内压力作用下径向截面上的拉应力。
第16页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
解：薄壁圆环 (δ<<d )在内压力作用下，径向截面上的 拉应力可认为沿壁厚均匀分布，故在求出径向截面上的法 FN s 向力FN后,用式 求拉应力。 b F FN R 2
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
§2-3 应力· 拉(压)杆内的应力
10KN 10KN
A=10mm2
哪个杆先破坏?
100KN 100KN
A=100mm2
在确定了拉(压)杆的轴力以后，并不能判断杆件是否 会因强度不足而破坏。因为轴力只是杆横截面上分布内力 系的合力，而要判断杆是否会因强度不足而破环，还必须 知道内力的分布集度，以及材料承受荷载的能力。
A0
F dF ，其 A dA
方向一般既不与截面垂直，也不与截面相切，称为总应力。
F
M
A
p
M
第4页
武生院建筑工程学院：材料力学
p
t
M 某一截面上法向分 法向分量 正应力s 布内力在某一点处 的集度
s
总应力 p 切向分量 切应力t
某一截面上切向分 布内力在某一点处 的集度
应力单位：Pa(1 Pa = 1 N/m2，1 MPa = 106 Pa)。
第二章 轴向拉伸和压缩
平均应力的定义
受力杆件(物体)某一截面的M点附近微面积ΔA上分布 内力的平均集度即平均应力， p
m
F ，其方向和大小一般 A
随所取ΔA的大小而不同。
F
M
A
第3页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
总应力定义：
该截面上M点处分布内力的集度为 p lim
圣维南原理已被实验所证实，故等直拉压杆的正应 力计算都可以以公式 s FN 为准。 A
第11页
武生院建筑工程学院：材料力学
3、最大正应力： 等直杆受几个轴向外力时，由轴力图可求得其最大轴
FN 力 FN ,max ，代入公式 s 可得杆内最大正应力为： A
最大轴力所在的横截面成为危险截面，危险截面上的 正应力为最大工作应力。
2. 即使是等直杆，在外力作用点附近，横截面上的应 力情况复杂，实际上也不能应用上述公式。 圣维南(Saint-Venant)原理：“力作用于杆端方式的不同， 只会使与杆端距离不大于杆的横向尺寸的范围内受到影响”。
第10页
武生院建筑工程学院：材料力学
第二章 轴向拉伸和压缩
圣维南(Saint-Venant)原理：“力作用于杆端方式的不同， 只会使与杆端距离不大于杆的横向尺寸的范围内受到影响”。