拉压杆横截面上的正应力.
- 格式:ppt
- 大小:158.00 KB
- 文档页数:5





1拉压杆横截面上的应力6.1.1 应力的概念同一种材料制成横截面积不同的两根直杆,在相同轴向拉力的作用下,其杆内的轴力相同。
但随拉力的增大,横截面小的杆必定先被拉断。
这说明单凭轴力F N 并不能判断拉(压)杆的强度,即杆件的强度不仅与内力的大小有关, 图6-1而且还与截面面积有关,即与内力在横截面上分布的密集程度(简称集度)有关,为此引入应力的概念。
要了解受力杆件在截面m-m 上的任意一点C 处的分布内力集度,可假想将杆件在m-m 处截开,在截面上围绕C 点取微小面积ΔA ,ΔA 上分布内力的合力为Δp (图6-1a),将Δp 除以面积ΔA ,即Ap p ∆∆=m (6-1) p m 称为在面积ΔA 上的平均应力,它尚不能精确表示C 点处内力的分布状况。
当面积无限趋近于零时比值Ap ∆∆的极限,才真实地反映任意一点C 处内力的分布状况,即 lim 0dAdp A p p A =∆∆=→∆ (6-2) 上式p 定义为C 点处内力的分布集度,称为该点处的总应力。
其方向一般既不与截面垂直,也不与截面相切。
通常,将它分解成与截面垂直的法向分量和与截面相切的切向分量(图6-1b ),法向分量称为正应力,用σ 表示;切向分量称为切应力,用τ表示。
将总应力用正应力和切应力这两个分量来表达具有明确的物理意义,因为它们和材料的两类破坏现象——拉断和剪切错动——相对应。
因此,今后在强度计算中一般只计算正应力和切应力而不计算总应力。
应力的单位为“帕”,用Pa 表示。
1Pa=1N/m 2, 常用单位为兆帕MPa ,1MPa=106Pa=1MN/mm 2=1N/mm 2,1GPa=109Pa 。
6.1.2 轴向拉伸和压缩时横截面上的正应力取一等截面直杆,在其侧面作两条垂直于杆轴的直线ab 和 cd ,然后在杆两端施加一对轴向拉力F 使杆发生变形,此时直线ab 、 cd分别平移至a 'b '、 c 'd '且仍保持为直线(图6-2a )。
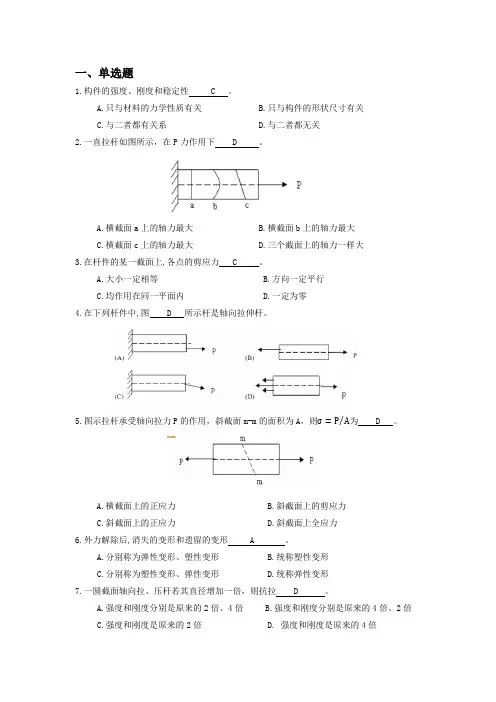
一、单选题1.构件的强度、刚度和稳定性 C 。
A.只与材料的力学性质有关B.只与构件的形状尺寸有关C.与二者都有关系D.与二者都无关2.一直拉杆如图所示,在P力作用下 D 。
A.横截面a上的轴力最大B.横截面b上的轴力最大C.横截面c上的轴力最大D.三个截面上的轴力一样大3.在杆件的某一截面上,各点的剪应力 C 。
A.大小一定相等B.方向一定平行C.均作用在同一平面内D.一定为零4.在下列杆件中,图 D 所示杆是轴向拉伸杆。
⁄为 D 。
5.图示拉杆承受轴向拉力P的作用,斜截面m-m的面积为A,则σ=P AA.横截面上的正应力B.斜截面上的剪应力C.斜截面上的正应力D.斜截面上全应力6.外力解除后,消失的变形和遗留的变形 A 。
A.分别称为弹性变形、塑性变形B.统称塑性变形C.分别称为塑性变形、弹性变形D.统称弹性变形7.一圆截面轴向拉、压杆若其直径增加一倍,则抗拉 D 。
A.强度和刚度分别是原来的2倍、4倍B.强度和刚度分别是原来的4倍、2倍C.强度和刚度是原来的2倍D. 强度和刚度是原来的4倍8.图中接头处的挤压面积等于 B 。
A.abB.cbC.lbD.lc9.单元体的受力状态如下图所示,已知上下两面的剪应力为τ则左右侧面上的剪应力为B 。
⁄ B.τ C.2τ D.0A.τ210.下图是矩形截面,则m-m线以上部分和以下部分对形心轴的两个静矩的 A 。
A.绝对值相等,正负号相同B.绝对值相等,正负号不同C.绝对值不等,正负号相同D.绝对值不等,正负号不同11.平面弯曲的变形特征是 D 。
A.弯曲时横截面仍保持为平面B.弯曲载荷均作用在同一平面内C.弯曲变形后的轴线是一条平面曲线D.弯曲变形后的轴线与载荷作用面同在一个平面内12.图示悬臂梁的AC段上,各个截面上的 A 。
A.剪力相同,弯矩不同B.剪力不同,玩具相同C.剪力和玩具均相同D.剪力和弯矩均不同13.当横向力作用于杆件的纵向对称面内时,关于杆件横截面上的内力与应力有以下四个结论。





截面正应力计算公式
1. 基本概念。
- 对于轴向拉压杆件,其横截面上的正应力计算公式为σ=(F_N)/(A)。
其中σ表示正应力,F_N为轴力(拉力为正,压力为负),A为横截面面积。
- 在计算轴力F_N时,通常采用截面法。
即假想地用一截面将杆件截开,研究其中一部分的受力平衡,从而确定轴力的大小和方向。
2. 梁弯曲时的正应力。
- 对于纯弯曲梁(梁的横截面上只有弯矩而无剪力的情况),其正应力计算公式为σ=(My)/(I_z)。
- 这里M为横截面上的弯矩,y为所求应力点到中性轴的距离,I_z为横截面对中性轴z的惯性矩。
- 对于横力弯曲(梁的横截面上既有弯矩又有剪力的情况),当梁的跨度l与横截面高度h之比l/h>5时,纯弯曲正应力公式σ=(My)/(I_z)仍可近似使用。
3. 组合变形下的正应力。
- 当杆件发生组合变形(如拉压与弯曲的组合、扭转与弯曲的组合等)时,可分别计算每种基本变形产生的正应力,然后根据叠加原理求出组合变形下的正应力。
- 例如对于拉压与弯曲组合变形的杆件,横截面上某点的正应力
σ=σ_N+σ_M,其中σ_N = (F_N)/(A)(拉压正应力),σ_M=(My)/(I_z)(弯曲正应力)。
第三章杆件横截面上的应力应变分析利用截面法可以确定静定问题中的杆件横截面上的内力分量,但内力分量只是横截面上连续分布内力系的简化结果,仅根据内力并不能判断杆件是否有足够的强度。
如用同一种材料制成粗细不同的两根杆,在相同的拉力作用下,两杆的轴力是相同的,当拉力增大时,细杆必定先被拉断。
这说明拉杆的强度不仅与轴力大小有关,还与横截面面积有关,因此还必须引入内力集度的概,即应力的概念。
本章在此基础上分别讨论了杆件在拉压、扭转和弯曲三种基本变形和组合变形下横截面上应力的分布规律,导出了应力计算公式,为后面对杆件进行强度计算打下了基础。
第一节应力、应变及其相互关系一、正应力、剪应力观察图3-1a所示受力杆件,在截面上围绕K点取微小面积,其上作用有微内力,于是在上内力的平均集度为:(3-1)亦称为面积上的平均应力。
一般来说截面上的内力并不均匀分布,因此平均应力随所取ΔA的不同而变化。
当ΔA趋向于零时,的大小方向都将逐渐趋于某一极限。
(3-2)式中,p称为K点的应力,它反映内力系在K点的强弱程度。
p是一个矢量,一般说既不与截面垂直,也不与截面相切。
通常将其分解为垂直于截面的应力分量和相切于截面的应力分量(图3-1b)。
称为正应力,称为切应力。
在国际单位制中,应力的单位是牛顿/米2(N/M2),称为帕斯卡,简称帕(Pa)。
由于这个单位太小,通常使用兆帕(MPa),1MPa = 106Pa。
二、正应变、切应变杆件在外力作用下,其尺寸或几何形状将发生变化。
若围绕受力弹性体中任意点截取一个微小正六面体(当六面体的边长趋于无限小时称为单元体),六面体的棱边边长分别为Δx 、Δy 、Δz (图3-2 )。
把该六面体投影到xy平面(图3-2b)。
变形后,六面体的边长和棱边夹角都将发生变化(图3-2c)。
变形前长为Δx的线段MN,变形后长度为Δx+Δs。
相对变形(3-3)表示线段MN单位长度的平均伸长或缩短,称为平均应变。
当Δx趋向于零,即点N趋向于M点时,其极限为(3-4)式中,ε称为M点沿x方向的线应变或正应变,ε为无量纲量。
材料⼒学的基本计算公式-材料⼒学弯曲公式1.弯矩、剪⼒和荷载集度之间的关系式2?轴向拉压杆横截⾯上正应⼒的计算公式Cr=杆件横截⾯轴⼒刊,横截⾯⾯积仏拉应⼒为正)3. 轴向拉压杆斜截⾯上的正应⼒与切应⼒计算公式(夹⾓a从X轴正⽅向逆时针转⾄外法线的⽅位⾓为正)4. 纵向变形和横向变形(拉伸前试样标距1,拉伸后试样标距11;拉伸前试样直径d,拉伸后试样直径dl)M = I l-I M = d l-d5. 纵向线应变和横向线应变6.泊松⽐外⼒偶KI N⾎矩计箕公式(P功率,n转速)T a = P a Sinaf= CrCDSafailIa= —siπ2α2Cr= EE7.胡克定律17?&受多个⼒作⽤的杆件纵向变形计算公式?9?承受轴向分布⼒或变截⾯的杆件,纵向变形计算公式14.剪切胡克定律(切变模量G 9切应变g ) T=G^ 15. 拉压弹性模量E 泊松⽐"和切变模量G 之间关系T 9所求点到11. 许⽤应⼒H=?脆性材料⾎=还,塑性材料氐=还12.延伸率 L -I 5- 1X100%110.轴向拉压杆的强度计算公式13. 截⾯收缩率A A-A IΨ= X100%圆截⾯对⼼的极惯性矩(a )实⼼圆(b )空⼼轴扭转时横截⾯上任⼀点切应⼒计算公式(扭矩32T18.圆截⾯周边各点处最⼤切应⼒计算公式19? 扭转截⾯系数Wrr=≠, (a )实⼼圆Wl=^(b )空⼼圆I 鲁(I F20.薄壁圆管(壁厚δ ≤ R o /10 , R o 为圆管的平均半21.圆轴扭转⾓炉与扭矩7;杆长⼈扭转刚度GHP 的关径不同(如阶梯轴)时23.等直圆轴强度条件24.塑性材料E = (WA)I 叫脆性材料I T l = (°?8 ~ Io )I er lGi I TT26. 受压圆筒形薄壁容器横截⾯和纵截⾯上的应⼒计径)扭转切应⼒计算公式T ~2τ^δTL 系式"瓯22同⼀材料制成的圆轴各段的扭矩不同或各段的直扭转圆轴的刚度条件?乳≤l^lZ 或27. 平⾯应⼒状态下斜截⾯应⼒的⼀般公式Cr K + 6 6 —VCre =—2 —+—2 —c∏s2a-τx≡m2α28. 平⾯应⼒状态的三个主应⼒tan2α? =-―啦-29?主平⾯⽅位的计算公式∏30.31. 受扭圆轴表⾯某点的三个主应⼒°ι=r, 5 =0,三向应⼒状态最⼤与最⼩正应⼒H=巧,?? =σ?33.三向应⼒状态最⼤切应⼒宁34.⼴义胡克定律El =丘冋⼀叭円+如】 =—IOi-V(σ?+σi)l= jlσr3-v(o1+σ2)j⾯最⼤切应⼒35.四种强度理论的相当应⼒40. 平⾏移轴公式(形⼼轴ZC与平⾏轴ZI的距离为a, 图形⾯积为M)4 =亿+^4_ My41. 纯弯曲梁的正应⼒计算公式σ~42. 横⼒弯曲最⼤正应⼒计算公式50.弯曲正应⼒强度条件^rIiaX43.矩形、圆形、空⼼圆形的弯曲截⾯系数?44.中性轴⼀侧的横截⾯对中性轴Z 的静矩,b 为横截⾯在45. 矩形截⾯梁最⼤弯曲切应⼒发⽣在中性轴处46.⼯字形截⾯梁腹板上的弯曲切应⼒近似公式47. 轧制⼯字钢梁最⼤弯曲切应⼒计算公式49.圆环形薄璧截⾯梁最⼤弯曲切应⼒发⽣在中性轴⼏种常见截⾯的最⼤弯曲切应⼒计算公式(Ema X 为51. ⼏种常见截⾯梁的弯曲切应⼒强度条件52. 弯曲梁危险点上既有正应⼒o⼜有切应⼒τ作⽤时的强度条件% =3⼗卅或% = 3⼭ M㈣,[σj = o? ItlSd2w_ M(X)53. 梁的挠曲线近似微分⽅程^r = -^a_ J■⼚54. 梁的转⾓⽅程^?dx+cι55.梁的挠曲线⽅程?窖W+⾦556.轴向荷载与横向均布荷载联合作⽤时杆件截⾯底部边缘和顶部边缘处的正应⼒计算公式偏⼼拉伸(压缩).-?,÷.M≡.σι∣ιaxGuin .58.建⽴的强度条件表达式幻嗚何TF如^4 = ^λ?2+0.75Γ2≤[σ]59⼆圆截⾯杆横截⾯上有两个弯矩叫和MZ同时作⽤时,合成弯矩为M =何硕60.圆截⾯杆横截⾯上有两个弯矩%和MZ 同时作⽤时—?2 +0.75Γ2 = — +ΛfJ +0.75Γ2 ≤[<τj62.弯拉扭或弯压扭组合作⽤时强度计算公式F63. 剪切实⽤计算的强度条件FHX ? r164. 挤压实⽤计算的强度条件%卞⼀%65.等截⾯细长压杆在四种杆端约束情况下的临界⼒66.压杆的约束条件:(a)两端较⽀U=I(b) ⼀端固定、⼀端⾃由µ=2 67. 压杆的长细⽐或柔度计算公式" 68. 细长压杆临界应⼒的欧拉公式% = ^~λ> λt =兀69.欧拉公式的适⽤围61.Ii = ----- = --- 王70. 压杆稳定性计算的安全系数法% F l71. 压杆稳定性计算的折减系数法Cr=?≤72. …关系需查表求得。