轴向拉压杆件应力

变截面圆杆轴向拉压时的应力分析在工程结构设计和力学分析中，经常会涉及到圆杆的轴向拉压情况。

变截面圆杆轴向拉压时，需要进行应力分析来评估其强度和稳定性。

本文将从变截面圆杆的应变分析、应力分析及强度评估三个方面进行详细阐述。

首先，我们来看变截面圆杆的应变分析。

对于一个轴向受拉力F作用下的圆杆，根据拉伸应变的定义，应变ε=△L/L，其中△L为杆件拉伸后的长度增量，L为杆件的初始长度。

对于直径为d1、d2的两个不同截面的圆杆，它们的初始长度相同，即L1=L2=L。

假设两个不同截面的圆杆受到相同的拉伸力F，根据应变的定义，应变ε1=△L1/L,ε2=△L2/L。

由于△L1和△L2相同，所以ε1和ε2的大小仅取决于截面直径的大小。

当杆截面直径越大，即d1>d2时，应变ε1>ε2，即在截面直径较大的地方应变更大，而在截面直径较小的地方应变较小。

这说明在变截面圆杆的拉伸过程中，截面直径较大的地方应变较大，即应力集中。

接下来，我们来探讨变截面圆杆的应力分析。

根据胡克定律，杆件内的应力与应变成正比。

对于同一截面的圆杆，内部各点的应力大小相同，在轴向拉伸的情况下，圆杆通过截面的轴向拉力均等。

然而，在变截面圆杆的轴向拉压过程中，不同截面处的应力是不同的。

如上述应变分析中所述，截面直径较大的地方应变更大，那么根据胡克定律，截面直径较大的地方应力也更大。

因此，在截面直径较大的地方，应力集中，容易产生应力集中现象。

这就要求我们在杆件设计时，要尽量避免或减小应力集中的情况。

最后，我们来评估变截面圆杆的强度。

材料的抗拉强度是指材料能够承受的最大拉伸力。

当变截面圆杆的拉力超过了材料的抗拉强度时，杆件就会发生塑性变形或断裂。

根据材料力学的知识，破坏材料的拉伸强度与截面面积成正比，而与截面形状无关。

因此，在设计变截面圆杆时，要根据材料的抗拉强度选择适当的截面面积，以确保杆件在拉伸过程中不发生塑性变形或断裂。

综上所述，变截面圆杆的应力分析是评估其强度和稳定性的重要步骤。

公式：1、轴向拉压杆件截面正应力N F Aσ=，强度校核max []σσ≤2、轴向拉压杆件变形N i i iF l l EA ∆=∑3、伸长率：1100%l l lδ-=⨯断面收缩率：1100%A A Aψ-=⨯4、胡克定律：E σε=，泊松比：'ευε=-，剪切胡克定律：G τγ=5、扭转切应力表达式：T I ρρτρ=，最大切应力：m ax PPT T R I W τ==，44(1)32P d I πα=-，34(1)16P d W πα=-，强度校核：m ax m ax []PT W ττ=≤6、单位扭转角：P d T dxG I ϕθ==，刚度校核：m axm ax []PTG I θθ=≤，长度为l 的一段轴两截面之间的相对扭转角PTl G I ϕ=，扭转外力偶的计算公式：()(/m in)9549K W r p M e n =7、薄壁圆管的扭转切应力：202T R τπδ=8、平面应力状态下斜截面应力的一般公式：cos 2sin 222x yx yx ασσσσσατα+-=+-，sin 2cos 22x yx ασστατα-=+9、平面应力状态三个主应力：'2x yσσσ+=+''2x yσσσ+=-，'''0σ=最大切应力m ax '''2σστ-=±=最大正应力方位02tan 2xx yτασσ=--10、第三和第四强度理论：3r σ=，4r σ=11、平面弯曲杆件正应力：ZM y I σ=，截面上下对称时，ZM W σ=矩形的惯性矩表达式：312Z bhI =圆形的惯性矩表达式：44(1)64Z d I πα=-矩形的抗扭截面系数：26Z bh W =，圆形的抗扭截面系数：34(1)32Z d W πα=-13、平面弯曲杆件横截面上的最大切应力：maxmax *S z S ZF S F K bI Aτ==14、平面弯曲杆件的强度校核：（1）弯曲正应力m ax []t t σσ≤，m ax []c c σσ≤ （2）弯曲切应力max []ττ≤（3）第三类危险点：第三和第四强度理论 15、平面弯曲杆件刚度校核：叠加法m ax []w w ll≤，m ax []θθ≤16、（1）轴向载荷与横向载荷联合作用强度： max max min ()N ZF M AW σσ=±（2）偏心拉伸(偏心压缩)：m ax m in ()N ZF F AW δσσ=±（3）弯扭变形杆件的强度计算：3[]r Z σσ==≤4[]r Zσσ==≤。

变截面圆杆轴向拉压时的应力分析杆材在轴向受拉压载荷作用下，会产生应力。

这个应力是由于承受载荷而引起的，它的大小和载荷的大小成正比。

变截面圆杆在轴向受拉压下的应力分析可以通过以下步骤来进行：1.杆材受力分析：首先需要了解杆材受力的具体情况。

假设杆材的长度为L，杆材的两个端部受到拉力F1和F2的作用。

这两个拉力可以是大小不等的，也可以是相等的。

在应力分析中，我们假设了杆材的两个端部的面积相等。

2. 悬链线条法：为了进行应力分析，我们可以使用悬链线条法。

该方法通过假设杆材上每个截面的应力呈像状分布，将杆材分为无数个小段。

我们考虑杆材上的一个小段dx，并考虑该小段受到的拉力。

3. 小段的受力分析：我们假设该小段的长度为dx，面积为A，根据杆材受力平衡条件，可以得出该小段受到的拉力为dF。

根据力和面积之间的关系，可以得出该小段受到的应力为σ = dF / A。

4.应力的积分：通过将杆材分为无数个小段，可以得到每个小段的应力。

然后将这些小段的应力积分起来，即可得到整个杆材的应力。

积分过程可以使用定积分来进行。

5.应力的变化情况：通过应力的积分，我们可以了解杆材上应力的变化情况。

通常情况下，杆材的应力在中部最大，在两端逐渐减小。

这是因为在中部受力最大，而在两端受力较小。

以上是变截面圆杆轴向拉压时的应力分析的基本步骤。

需要注意的是，在进行应力分析时，我们假设了杆材是均匀的、材料是线弹性的，并且未考虑杆材的弯曲变形。

在实际工程中，进行应力分析时需要根据具体的情况和材料的特性进行修正。

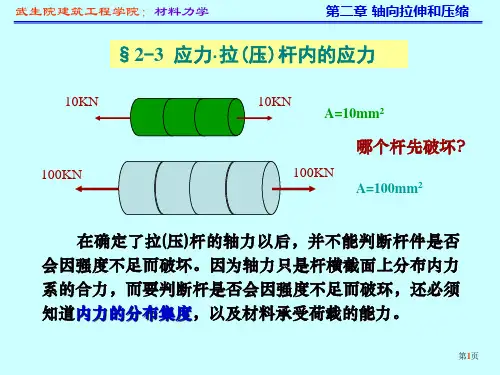
§4-3 轴向拉(压)杆的应力1．应力的概念为了解决杆件的强度问题，不仅要知道当外力达到一定值时杆件可能沿哪个截面破坏，而且还要知道该截面上哪个点首先开始破坏。

因而仅仅知道杆件截面上内力的合力是不够的，还需要进一步研究截面上内力的分布情况，从而引入了应力的概念。

应力就是杆件截面上分布内力的集度。

若考察某受力杆截面m-m 上M 点处的应力，如图4-8所示。

图4-8 一点的应力在M 点周围取一很小的面积A ∆，设A ∆面积上分布内力的合力为F ∆，则面积A ∆上内力F ∆的平均集度为A F p m ∆∆= (4-1) 式中m p 称为面积A ∆上的平均应力。

当微小面积A ∆趋近于零时，就得到截面上M 点处的总应力，即dA dFA Fp A =∆∆==∆lim 0(4-2) 由于F 是矢量，故P 也是矢量，其方向一般不与截面垂直或平行，因此可以分解成与截面垂直的法向分量正应力σ和与截面向切的切向分量切应力(剪应力)τ。

从应力的定义可知，应力是与“截面”和“点”这两个因素分不开的。

一般地说，杆件在外力作用下，任一截面上不同点的应力值是不同的，同一点位于不同截面上的应力值也是不同的。

因此在谈内力时，应明确是哪个截面哪个点处的应力。

应力的量纲为⎥⎦⎤⎢⎣⎡2长度力，其国际单位为Pa(帕斯卡)，1Pa=1牛顿/米2。

工程中常用MPa ，1MPa=106Pa 。

2．拉(压)杆横截面上的应力对于拉(压)杆，横截面上的内力为轴力F N ，与轴力对应的应力为正应力σ。

观察受拉等直杆(图4-9(a))的变形情况。

首先在等直杆侧面作两条横向线ab 和cd ，代表其横截面，然后在杆的两端施加一对轴向拉力F 使杆发生变形。

可以观察到，横向线ab 和cd 移动到a’b’和c’d’的位置了，如图4-9(b)所示。

对于压杆，同样可以观察到该现象。

根据这一现象，可以假设原为平面的横截面在杆变形后仍为平面，即平面假设。

根据这一假设，拉(压)杆变形后两横截面将沿杆轴线方向作相对平移，也就是说，拉(压)杆在其任意两个横截面之间纵向线段的伸长变形是均匀的。

截面正应力计算公式
1. 基本概念。

- 对于轴向拉压杆件，其横截面上的正应力计算公式为σ=(F_N)/(A)。

其中σ表示正应力，F_N为轴力（拉力为正，压力为负），A为横截面面积。

- 在计算轴力F_N时，通常采用截面法。

即假想地用一截面将杆件截开，研究其中一部分的受力平衡，从而确定轴力的大小和方向。

2. 梁弯曲时的正应力。

- 对于纯弯曲梁（梁的横截面上只有弯矩而无剪力的情况），其正应力计算公式为σ=(My)/(I_z)。

- 这里M为横截面上的弯矩，y为所求应力点到中性轴的距离，I_z为横截面对中性轴z的惯性矩。

- 对于横力弯曲（梁的横截面上既有弯矩又有剪力的情况），当梁的跨度l与横截面高度h之比l/h>5时，纯弯曲正应力公式σ=(My)/(I_z)仍可近似使用。

3. 组合变形下的正应力。

- 当杆件发生组合变形（如拉压与弯曲的组合、扭转与弯曲的组合等）时，可分别计算每种基本变形产生的正应力，然后根据叠加原理求出组合变形下的正应力。

- 例如对于拉压与弯曲组合变形的杆件，横截面上某点的正应力
σ=σ_N+σ_M，其中σ_N = (F_N)/(A)（拉压正应力），σ_M=(My)/(I_z)（弯曲正应力）。

第3章杆件的应力与强度判断1、“轴向拉压杆件任意斜截面上的内力作用线一定与杆件的轴线重合”2、“拉杆内只存在均匀分布的正应力，不存在剪应力。

”3、“杆件在轴向拉压时最大正应力发生在横截面上”4、“杆件在轴向拉压时最大剪应力发生在与轴线成45度角的斜截面上”5、“材料的延伸率与试件的尺寸有关。

“6、“没有明显的屈服极限的塑性材料，可以将产生0.2％应变时的应力作为屈服极限。

“7、“构件失效时的极限应力是材料的强度极限。

”8、“对平衡构件，无论应力是否超过弹性极限，剪应力互等定理均成立。

”9、“直杆扭转变形时，横截面的最大剪应力在距截面形心最远处。

”10、“塑性材料圆轴扭转时的失效形式为沿横截面断裂”11、“对于受扭的圆轴，最大剪应力只出现在横截面上”12、”圆轴受扭时，横截面的最大剪应力发生在距截面形心最远处。

”13、“圆轴受扭时，轴内各点均处于纯剪切状态“14、”薄壁圆管与空心圆管的扭转剪应力计算公式完全一样。

”15、”圆轴的扭转变形实际上是剪切变形。

”16、”圆轴扭转时，根据剪应力互等定理，其纵截面上也存在剪应力。

”17、“剪应力互等定理只适用于纯剪状态”18、“传动轴的转速越高，则其横截面的直径应越大”19、“受扭杆件的扭矩仅与杆件所受的外力偶矩有关，而与杆件的材料、横截面的大小以及横截面的形状无关”20、“普通碳钢扭转屈服极限τs=120MPa，剪变模量G=80GPa，则由剪切虎克定律τ=Gγ得到剪应变为γ=1.5×10-3rad”21、“一等直圆杆，当受到扭转时，杆内沿轴线方向会产生拉应变。

”22、“低碳钢圆柱试件受扭时，沿450螺旋面断裂。

”23、“铸铁圆柱试件受扭时，沿横截面断裂”24、“弯曲时梁横截面的中性轴通过截面形心。

”25、“梁的截面如图，其抗弯截面系数为W Z＝BH2/6-bh2/6”26、“控制弯曲强度的主要因素是最大弯矩值”27、“设梁某段承受正弯矩的作用，则靠近顶面和靠近底面的纤维分别是伸长的和缩短的”28、“中性轴是梁的中性层与横截面的交线。

轴向拉压杆件横截面上的应力在工程设计和材料力学中，轴向拉压杆件是一种经常使用的结构元件，其横截面上的应力分布是一个重要的研究内容。

在此，将介绍轴向拉压杆件横截面上的应力分布，并给出相关参考内容。

轴向拉压杆件是指受到拉力或压力作用的杆件，其横截面形状可以是圆形、方形、矩形、椭圆形等。

在讨论轴向拉压杆件横截面上的应力分布时，我们假设该杆件是均匀材料、轴对称且受到等径向拉力或压力作用。

根据这些假设，我们可以得到以下结论。

首先，对于圆形横截面的轴向拉压杆件，应力沿着截面的半径方向是均匀的。

这意味着，在横截面上的任何一点，杆件的应力大小是相同的，只是方向不同。

具体而言，在拉力作用下，横截面上的应力大小为σ = F/A，其中F是作用于杆件上的拉力，A是横截面的面积。

而在压力作用下，横截面上的应力大小为σ = -F/A。

其次，对于矩形或方形横截面的轴向拉压杆件，其应力分布是非均匀的。

在拉力作用下，杆件的边缘处应力最大，中心处应力最小。

具体而言，在矩形或方形横截面的边缘处，应力计算公式为σ = F/2A，其中F是作用于杆件上的拉力，A是横截面的面积。

而在中心处，应力计算公式为σ = F/A。

此外，对于椭圆形横截面的轴向拉压杆件，其应力分布也是非均匀的。

在拉力作用下，杆件的长轴方向应力最大，短轴方向应力最小。

具体而言，在椭圆形横截面的长轴方向，应力计算公式为σ = F/2A，其中F是作用于杆件上的拉力，A是横截面的面积。

而在短轴方向，应力计算公式为σ = F/A。

综上所述，轴向拉压杆件横截面上的应力分布与杆件的形状密切相关。

在实际工程中，根据结构的要求，可以选择合适的截面形状来平衡应力分布，以提高杆件的强度和稳定性。

参考文献：1. 程训文等著. 材料力学. 北京：清华大学出版社，2016年2. 韩良辉等著. 结构力学. 北京：中国建筑工业出版社，2019年3. 林万善等著. 实用结构力学基础. 北京：中国水利水电出版社，2014年4. Beer, Ferdinand P., Johnston, E. Russell, DeWolf, John T. Mechanics of Materials. New York: McGraw-Hill Education, 2017.5. Popov, Egor P. Engineering Mechanics of Solids. Upper Saddle River, NJ: Pearson, 2015.。

轴向拉〔压〕杆横截面上应力
一、教学内容
知识目标：横截面上的应力计算、斜截面应力极值
能力目标：利用公式计算指定截面上的应力
二、教学重难点
重点：计算横截面上的应力
难点：计算斜截面上的应力
三、教学方法
采用线上线下混合式教学法、小组讨论法、启发式讲授法等方法。

四、教学实施
课前：通过云课堂APP进行公布课前任务：观看粉笔被拉断的截面形式
课中：
1.创设情境法：粉笔被拉断，引出应力的概念。

2.启发式讲授法讲解轴向拉压变形横截面上应力公式推导。

〔1〕动画观看轴向拉伸变形外表横向线纵向线变革。

〔2〕平面假设、单向受力假设；〔3〕启发式讲授横截面上应力分布规律及正应力公式求解过程。

3.经典例题讲授如何求解任意横截面上任意点的正应力。

课后：完成练习册习题。

五、教学小结
学生通过云课堂APP进行本次课程学习效果的评价；教师总结课程内容，并进行下次课程任务部署。