04-2.2 拉压杆的应力
- 格式:pdf
- 大小:570.11 KB
- 文档页数:14







材料力学章节重点和难点第一章绪论1.主要内容:材料力学的任务;强度、刚度和稳定性的概念;截面法、内力、应力,变形和应变的基本概念;变形固体的基本假设;杆件的四种基本变形。
2.重点:强度、刚度、稳定性的概念;变形固体的基本假设、内力、应力、应变的概念。
3.难点:第二章杆件的内力1.主要内容:杆件在拉压、扭转和弯曲时的内力计算;杆件在拉压、扭转和弯曲时的内力图绘制;平面弯曲的概念。
2.重点:剪力方程和弯矩方程、剪力图和弯矩图。
3. 难点:绘制剪力图和弯矩图、剪力和弯矩间的关系。
第三章杆件的应力与强度计算1.主要内容:拉压杆的应力和强度计算;材料拉伸和压缩时的力学性能;圆轴扭转时切应力和强度计算;梁弯曲时正应力和强度计算;梁弯曲时切应力和强度计算;剪切和挤压的实用计算方法;胡克定律和剪切胡克定律。
2.重点:拉压杆的应力和强度计算;材料拉伸和压缩时的力学性能;圆轴扭转时切应力和强度计算;梁弯曲时正应力和强度计算。
3.难点:圆轴扭转时切应力公式推导和应力分布;梁弯曲时应力公式推导和应力分布;第四章杆件的变形简单超静定问题1.主要内容:拉(压)杆的变形计算及单超静定问题的求解方法;圆轴扭转的变形和刚度计算;积分法和叠加法求弯曲变形;用变形比较法解超静定梁。
2.重点:拉(压)杆的变形计算;;圆轴扭转的变形和刚度计算;叠加法求弯曲变形;用变形比较法解超静定梁。
3.难点:积分法和叠加法求弯曲变形;用变形比较法解超静定结构。
第五章应力状态分析? 强度理论1.主要内容:应力状态的概念;平面应力状态分析的解析法和图解法;广义胡克定律;强度理论的概念及常用的四种强度理论。
2.重点:平面应力状态分析的解析法和图解法;广义虎克定律;常用的四种强度理论。
3.难点:主应力方位确定。
第六章组合变形1.主要内容:拉伸(压缩)与弯曲、斜弯曲、扭转与弯曲组合变形的强度计算;2.重点: 弯扭组合变形。
3.难点:截面核心的概念第七章压杆稳定1.主要内容:压杆稳定的概念;各种支座条件下细长压杆的临界载荷;欧拉公式的适用范围和经验公式;压杆的稳定性校核。



载荷与应力的计算公式载荷在机械零件上的载荷分为静载荷与变载荷两大类。
静载荷是指大小、作用位置与作用方向不随时间变化或缓慢变化的载荷,如锅炉压力。
变载荷是指大小、作用位置和方向随着时间变化的载荷,如汽车悬架弹簧和自行车的链条工作时所受载荷。
机械零、部件所受载荷分为名义载荷、工作载荷、计算载荷。
名义载荷是指在平稳工作条件下根据额定功率通过力学公式计算出来的载荷。
工作载荷是指机器正常工作时所受的实际载荷。
在通常情况下引入载荷系数来考虑工作时各种因素的影响。
载荷系数与名义载荷的乘积称为计算载荷。
应力根据时间变化的特性不同,将应力分为静应力和变应力。
静应力是指不随时间变化或缓慢变化的应力,如图所示,变应力是随时间变化的应力。
变应力形式多样,可分为规律性和随机性两种,其中规律性稳定变应力可归纳为非对称循环变应力、脉动循环变应力和对称循环变应力三种基本类型1.拉伸与压缩变形1.l拉(压)杆的应力1.1.1拉(压)杆横截面上的正应力拉压杆件横截面上只有正应力o,且为平均分布,其计算公式为F.o ='"{(3-1)A式中为该横F,截面的轴力﹐A为横截面面积。
正负号规定﹑拉应力为正,压应力为负。
公式(3-1)的适用条件:(1〕杆端外力的合力作用线与杆轴线重合,即只适于轴向拉(压)杆件:(2〕适用于离杆件受力区域稍远处的横闻;(3)杆件上有孔洞或凹槽时,该处将产生局部应力集中现象,横截面上应力分布很不均匀;(4)截面连续变化的直杆,杆件两恻棱边的夹角时α≤20°,可应用式(3-1)计算,所得结果的误约为3 %。
图3-1拉压杆件任意斜截面(a图)上的应力为平均分布,其计算公式为全应力P。
= o cosα(3-2)正应力o, = o cos o (3-3)切应力t。
=sin 2a《3-4)式中为横截o面上的应力。
正负号规定﹔a由横截面外法线转至斜哉面的外法线,逆时针转向为正,反之为负。
拉应力为正,压应力为值。
第三章 应力与强度计算一.内容提要本章介绍了杆件发生根本变形时的应力计算,材料的力学性能,以及根本变形的强度计算。
1.拉伸与压缩变形 1.1 拉〔压〕杆的应力1.1.1拉〔压〕杆横截面上的正应力拉压杆件横截面上只有正应力σ,且为平均分布,其计算公式为NF Aσ=(3-1) 式中N F 为该横截面的轴力,A 为横截面面积。
正负号规定 拉应力为正,压应力为负。
公式〔3-1〕的适用条件:〔1〕杆端外力的合力作用线与杆轴线重合,即只适于轴向拉〔压〕杆件; 〔2〕适用于离杆件受力区域稍远处的横截面;〔3〕杆件上有孔洞或凹槽时,该处将产生局部应力集中现象,横截面上应力分布很不均匀;〔4〕截面连续变化的直杆,杆件两侧棱边的夹角020α≤时,可应用式〔3-1〕计算,所得结果的误差约为3%。
1.1.2拉〔压〕杆斜截面上的应力〔如图3-1〕图3-1拉压杆件任意斜截面〔a 图〕上的应力为平均分布,其计算公式为 全应力cos p ασα= (3-2) 正应力2cos ασσα=〔3-3〕切应力1sin 22ατα=〔3-4〕式中σ为横截面上的应力。
正负号规定:α由横截面外法线转至斜截面的外法线,逆时针转向为正,反之为负。
ασ 拉应力为正,压应力为负。
ατ 对脱离体内一点产生顺时针力矩的ατ为正,反之为负。
两点结论:〔1〕当00α=时,即横截面上,ασ到达最大值,即()max ασσ=。
当α=090时,即纵截面上,ασ=090=0。
〔2〕当045α=时,即与杆轴成045的斜截面上,ατ到达最大值,即max ()2αατ=。
1.2 拉〔压〕杆的应变和胡克定律 〔1〕变形及应变杆件受到轴向拉力时,轴向伸长,横向缩短;受到轴向压力时,轴向缩短,横向伸长。
如图3-2。
图3-2轴向变形 1l l l ∆=- 轴向线应变 l lε∆=横向变形 1b b b ∆=- 横向线应变 b bε∆'=正负号规定 伸长为正,缩短为负。
第三章 应力与强度计算一.内容提要本章介绍了杆件发生基本变形时的应力计算,材料的力学性能,以及基本变形的强度计算。
1.拉伸与压缩变形1.1 拉(压)杆的应力1.1.1拉(压)杆横截面上的正应力拉压杆件横截面上只有正应力σ,且为平均分布,其计算公式为 NF Aσ=(3-1) 式中为该横N F 截面的轴力,A 为横截面面积。
正负号规定 拉应力为正,压应力为负。
公式(3-1)的适用条件:(1)杆端外力的合力作用线与杆轴线重合,即只适于轴向拉(压)杆件;(2)适用于离杆件受力区域稍远处的横截面; (3)杆件上有孔洞或凹槽时,该处将产生局部应力集中现象,横截面上应力分布很不均匀;(4)截面连续变化的直杆,杆件两侧棱边的夹角时020α≤,可应用式(3-1)计算,所得结果的误差约为3%。
1.1.2拉(压)杆斜截面上的应力(如图3-1)图3-1 拉压杆件任意斜截面(a 图)上的应力为平均分布,其计算公式为 全应力 cos p ασα= (3-2)正应力2cos ασσα=(3-3)切应力1sin 22ατα=(3-4) 式中为横截σ面上的应力。
正负号规定:α 由横截面外法线转至斜截面的外法线,逆时针转向为正,反之为负。
ασ 拉应力为正,压应力为负。
ατ 对脱离体内一点产生顺时针力矩的ατ为正,反之为负。
两点结论:(1)当00α=时,即横截面上,ασ达到最大值,即()m ax ασσ=。
当α=090时,即纵截面上,ασ=090=0。
(2)当045α=时,即与杆轴成045的斜截面上,ατ达到最大值,即m a x ()2αατ=。
1.2 拉(压)杆的应变和胡克定律 (1)变形及应变杆件受到轴向拉力时,轴向伸长,横向缩短;受到轴向压力时,轴向缩短,横向伸长。
如图3-2。
图3-2轴向变形 1l l l ∆=- 轴向线应变 llε∆=横向变形 1b b b ∆=- 横向线应变 bbε∆'=正负号规定 伸长为正,缩短为负。
轴向拉压杆件横截面上的应力在工程设计和材料力学中,轴向拉压杆件是一种经常使用的结构元件,其横截面上的应力分布是一个重要的研究内容。
在此,将介绍轴向拉压杆件横截面上的应力分布,并给出相关参考内容。
轴向拉压杆件是指受到拉力或压力作用的杆件,其横截面形状可以是圆形、方形、矩形、椭圆形等。
在讨论轴向拉压杆件横截面上的应力分布时,我们假设该杆件是均匀材料、轴对称且受到等径向拉力或压力作用。
根据这些假设,我们可以得到以下结论。
首先,对于圆形横截面的轴向拉压杆件,应力沿着截面的半径方向是均匀的。
这意味着,在横截面上的任何一点,杆件的应力大小是相同的,只是方向不同。
具体而言,在拉力作用下,横截面上的应力大小为σ = F/A,其中F是作用于杆件上的拉力,A是横截面的面积。
而在压力作用下,横截面上的应力大小为σ = -F/A。
其次,对于矩形或方形横截面的轴向拉压杆件,其应力分布是非均匀的。
在拉力作用下,杆件的边缘处应力最大,中心处应力最小。
具体而言,在矩形或方形横截面的边缘处,应力计算公式为σ = F/2A,其中F是作用于杆件上的拉力,A是横截面的面积。
而在中心处,应力计算公式为σ = F/A。
此外,对于椭圆形横截面的轴向拉压杆件,其应力分布也是非均匀的。
在拉力作用下,杆件的长轴方向应力最大,短轴方向应力最小。
具体而言,在椭圆形横截面的长轴方向,应力计算公式为σ = F/2A,其中F是作用于杆件上的拉力,A是横截面的面积。
而在短轴方向,应力计算公式为σ = F/A。
综上所述,轴向拉压杆件横截面上的应力分布与杆件的形状密切相关。
在实际工程中,根据结构的要求,可以选择合适的截面形状来平衡应力分布,以提高杆件的强度和稳定性。
参考文献:1. 程训文等著. 材料力学. 北京:清华大学出版社,2016年2. 韩良辉等著. 结构力学. 北京:中国建筑工业出版社,2019年3. 林万善等著. 实用结构力学基础. 北京:中国水利水电出版社,2014年4. Beer, Ferdinand P., Johnston, E. Russell, DeWolf, John T. Mechanics of Materials. New York: McGraw-Hill Education, 2017.5. Popov, Egor P. Engineering Mechanics of Solids. Upper Saddle River, NJ: Pearson, 2015.。
材料力学大连理工大学王博
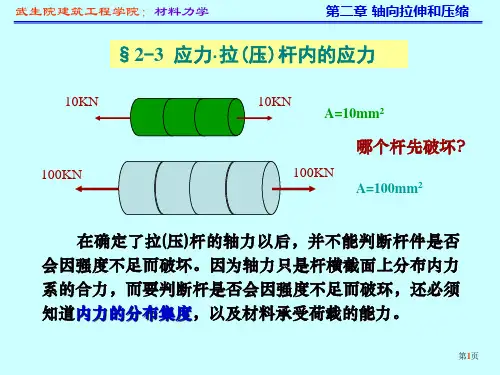
拉压杆的应力
判断:1 已知轴力求应力,这是静不定问题 2 需要研究变形才能解决
思路:
应力表达式 (由内力表示应力) 观察变形(外表)
变形假设(内部) 应变分布 应力分布 回顾:
应力的点、方向等概念 变形协调 物理关系 静力学条件
拉压杆的应力
F 1
F 2
1.
变形特点
纵线——仍为直线,平行于轴线横线——仍为直线,且垂直于轴线F
F 纵线横线
一、横截面上的应力
2. 平面假设 Plane cross-section assumption 杆件的任意横截面在杆件受力变形后
仍保持为平面, 且与轴线垂直。
3.应变分布
由平面假设,轴向应变分布是均匀的
4.应力分布
由均匀性假设,横截面上的应力也是均匀分布的,即各点应力相同
5. 应力公式
由平衡关系,横截面上 因此,拉压杆横截面上只存在正应力
静力学关系 ∴ d A σd A
N d F A A
σσ==⎰N F A
σ=0
τ=
F F F F
F 问题: 两杆横截面的正应力分布是否相同?
小讨论
N F A σ=N F A σ=F
原理:等效力系只影响
荷载作用点附近局部区
域的应力和应变分布。
结论:无论杆端如何受力,拉压杆横截面的正应力均可用下式计算: 二、圣维南(Saint-Venant ,1797-1886) 原理
N F A
σ=
F
A
C B
45º 2 1
例题
已知:A 1= 1000 mm 2, A 2= 20000 mm 2, F = 100 kN 求:各杆横截面的应力 ∑F y = 0, F N1 sin45°-F = 0 解:⑴ 轴力计算 取结点A 100221N ⨯==F F = 141.4 kN =-100 kN ∑F x = 0, -F N1cos45°-F N2 = 0 F N2 =-F N1cos45°
=-141.4 cos45° 45° F N2 F N1 A F x y
⑵ 应力计算 例题
F N1 = 141.4 kN F N2 =-100 kN ()+=⨯==MPa 4.1411000104.141311N 1A F σ()
--=⨯-==MPa
520000
10100322N 2A F σF
A C B
45º 2 1 45° F N2 F N1 A
F x y
三、斜截面的应力
拉压杆横截面上没有切应力,只有正应力,斜截面上
是否也是这样?
观察一个现象:
F N F N F N F N
横截面面积 A 正应力σ =F /A 斜截面面积 内力 全应力 分解:正应力和切应力 p α
P α 斜截面上的应力
F F k
k
α
F k k
α /cos A A αα=/cos p P A ααασα==F k
k α
α ασατp α α
σασαα2cos cos ==p α
σ
αασαταα2sin 2sin cos sin ===p P F α=
讨论
可见,斜截面上既有正应力,也有切应力。
F k k α
α ασατp α α
σ
τα2sin 2=ασσα2cos =(1) 0α=: max ασσ=, 0
ατ=(2) 45α=: /2ασσ=, max
/2ατσ=(3) 90α=: 0ασ=, 0ατ=。