当前位置：文档之家 › 应力莫尔圆应力平衡微分方程

应力莫尔圆应力平衡微分方程

  • 格式：pptx
  • 大小：4.80 MB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

02讲-应力与平衡、位移与应变 PPT

02讲-应力与平衡、位移与应变 PPT

用转轴公式能求得斜面上的 正应力和剪应力。
王正伟
主应力
Principal Stress
对于给定的应力状态，若改变斜面方向，则斜面应力的大小和 方向都会发生改变，因此是否存在一个面，使得只存在正应力 而无剪应力？
() g
x xy xz
xy y
yz
xz yz 0 z
1、2、3
、2、3
王正伟
主应力的性质 Principal Stress
在笛卡尔坐标系中，用六个平行于坐标面的截面在一点周 围截取一个正六面体微元。正六面体的六个面法向矢量与坐标 轴平行，同向的三个面称之为正面，反向的三个面称之为负面。 将作用在正面上的应力矢量沿坐标轴方向分解。
1 xxi xy j xzk
2 yxi yy j yzk
3 zxi zy j zzk
王正伟
外力、载荷 Load
面力是作用在物体表面上的 外力。
p lim F S 0 S
体积力是作用在物体内部体积 上的外力。
F f lim
V 0 V
王正伟
应力矢量(应力) Stress Vector
应力矢量(应力)
( )
lim S0
F S
若取 S 为变形前面元的初始面积，则上式给出工程应力，亦称 名义应力，常用于小变形情况。 对于大变形问题，应取 S 为变形后面元的实际面积，称真实应 力，简称真应力, 也称柯西应力。
四面体体积为：
V 1dhdS 3
王正伟
斜面应力公式 Cauchy Formula
四面体平衡条件为：
(1) dS1 (2) dS2 (3) dS3
()
dS
f
(1dhdS) 3
0

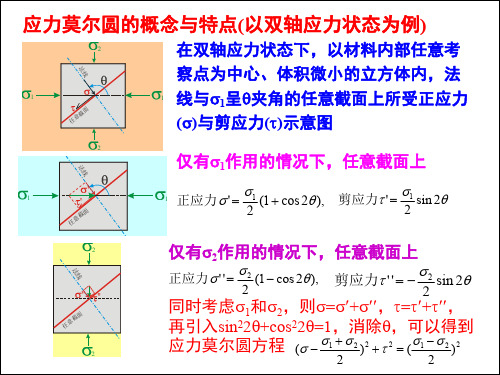
应力莫尔圆

应力莫尔圆

（，）分别代表法线与 最大主应力轴1呈夹角 的那个截面上所受到的正
N力与剪应力。
平面应力状态的应力莫尔圆
应力莫尔圆的概念与特点(以双轴应力状态为例)
1．双轴应力状态的特点
（1）剪应力互等定律：两个相互垂直的截面上 受到的剪应力大小相等，符号相反；
（2）两个相互垂直的截面 上受到的正应力之和不变，
(

1

2
)2

2

(
1
2
)2
2
2
应力莫尔圆的概念与特点(以双轴应力状态为例)
以横坐标代表正应力，纵坐标代表剪应力，建立
－ 坐标系，一点的应力状态在该坐标系中可以表
示为一个圆的方程
(

1
2
)2

2


(
1
2
)2
2
2
这个圆就是该点的应力莫 尔圆，圆上某点的坐标
T A( , )
应力莫尔圆的概念与特点以双轴应力状态为例在双轴应力状态下以材料内部任意考察点为中心体积微小的立方体内法呈夹角的任意截面上所受正应力与剪应力示意图作用的情况下任意截面上同时考虑21消除可以得到应力莫尔圆方程应力莫尔圆的概念与特点以双轴应力状态为例以横坐标代表正应力纵坐标代表剪应力建立坐标系一点的应力状态在该坐标系中可以表示为一个圆的方程平面应力状态的应力莫尔圆这个圆就是该点的应力莫分别代表法线与最大主应力轴呈夹角的那个截面上所受到的正应力与剪应力
2
2
法线
2
'' ''
面 截 意 任
2
仅有2作用的情况下，任意截面上
正应力 ' ' 2 (1 cos 2 ), 2

第1章应力分析及应力平衡微分方程

第1章应力分析及应力平衡微分方程

沈阳工业大学
1.1.1 应力
一，连续介质模型
连续介质是一种理论模型．该模型认为物质 连续地分布在物体所占有的空间之内．要研究物 体的宏观机械运动，可以取连续介质的质点，实 际上是物质的微块，它的尺度与所研究的宏观尺 度相比充分小，这样在微块内，每一个物理量都 可以看作均匀分布的常量．而数学上把这微块当 作一个点来处理．另一方面，又要求这微块的尺 度与分子运动的尺度足够大，使微块包含大量分 子，从而对分子的运动作统计平均．以得到表征 宏观现象的物理量．因此对微块要求宏观小，微 观大．
第1章 应力分析
沈阳工业大学
第 1 章 应力分析
1.1 点的应力状态 1.2特殊应力状态 1.3应力平衡微分方程
沈阳工业大学
1.1 点的应力状态
1.1 .1应力 1.1.2 点的应力状态 1.1.3主应力及应力张量不变量 1.1.4主切应力和最大切应力 1.1.5应力偏张量和应力球张量 1.1.6八面体应力和等效应力 1.1.7应力莫尔圆
沈阳工业大学
1.1.1 应力
一，外力(Load)
塑性成型是利用金属的塑性，在外力的作用下使其 成型的一种方法．作用于金属的外力可以分两类：一 类是作用于金属表面上的力，称为面力，它可以是集 中力也可以是分布力，一般由加工设备和模具提供； 另一类是作用于金属物体每个质点上的力，称为体积 力．如重力、磁力、惯性力等等。
Ｆ１
沈阳工业大学
1.1.1 应力
应力Sｎ 是内力的集度
内力和应力均为矢量
应力的单位： 1Pa=1N/m2=1.0197Kgf/mm2
1MPa=106N/m2
应力是某点A的坐标的函数，即
受力体内不同点的应力不同。
应力是某点A在坐标系中的方向 Ｆ３ Ｆ２

第1章应力分析及应力平衡微分方程

第1章应力分析及应力平衡微分方程

，可以把σij（Stress tensor ）分解成与体积变化有关 的量和形状变化有关的量。前者称为应力球张量
(Spherical stress tensor) ，后者称为应力偏张量
(Deviatoric stress tensor) 。设σm为平均应力，则有
m
1 3
(
x
y
z)
按照应力叠加原理，σij具有可分解性。因此有
整理后可得S：zdA xzdAx yzdAy zdAz
求和约定： 全应力：
Sx xl yxm zxn S y xyl ym zyn Sz xzl yzm zn
S j ijli
S2
S
2 x
Sy2
Sz2
很重要！ （１－１）
（１－２）
沈阳工业大学
1.1.２ 点的应力状态
由于微元体处于静力平衡状态，所以，绕其各轴 的合力矩为零，因此可以得到
xy= yx, yz= zy zx= xz 称为剪应变互等定律
沈阳工业大学
1.1.２ 点的应力状态
一，一点的应力状态：是指通过变形体内某点的 单元体所有截面上的应力的有无、大小、方向等 情况。
一点的应力状态的描述
（１） 数值表达：x=50MPa，xz=35MPa （２） 图示表达：在单元体的三个正交面上标
第1章 应力分析
沈阳工业大学
第 1 章 应力分析
1.1 点的应力状态 1.2特殊应力状态 1.3应力平衡微分方程
沈阳工业大学
1.1 点的应力状态
1.1 .1应力 1.1.2 点的应力状态 1.1.3主应力及应力张量不变量 1.1.4主切应力和最大切应力 1.1.5应力偏张量和应力球张量 1.1.6八面体应力和等效应力 1.1.7应力莫尔圆

3-1-4 应力分析_应力莫尔圆及应力平衡微分方程

3-1-4 应力分析_应力莫尔圆及应力平衡微分方程

10 3 10
l1=
10 1
m2= 10
最大切应力τmax=500MPa
金属塑性成形原理
解析法验证：
2 3 0
三个不变量： J1 x y z 4
J2
(x y
yz
zx )
2 xy
2 yz
2 zx
21
ij 3
0
6 0(100MPa) 0 0
J3
x
y z
2 xy
yz zx
( x
金属塑性成形原理
练习题1： 应用莫尔圆分析单向拉伸时的各横截面上的应力变化状态。
y B（ σy＝40 τyx＝0 ） θ
τ C (0,20)
2θ
A
A
（ σx＝0 τxy＝0 ）
Bσ
(40,0)
x
当2θ＝90°（θ＝45°）时，截面的剪切力 达到最大值20MPa
金属塑性成形原理
练习题2：物体中某点为平面应力状态，应力张量为：
试利用莫尔圆图解主应力,主方向和最大切应力
τ
τmax (0,5)
2 3 0
ij 3 6 0(100MPa)
0 0 0
2α2
B(6,3)
σ2 (-3,0) 2β2
A(-2,-3) σ2＝－3
2α1 σ1(7,0)
O(2,0) D
σ
2β1 σ1＝7
OD的长度＝1/2（6+2）＝4；R＝5；
y
B
以应力主轴为坐标轴，作一斜微分面，其方向
余弦为l，m，n，则有 :
金属塑性成形原理
l2 m2 n2 1
S1 1 l S2 2 m S3 3 n S 2 S12 S22 S32 12l 2 22m2 32n2

金属塑性成形原理期末复习

金属塑性成形原理期末复习
（2）变形时的外部条件，如变形温度、变形速度、 应力状态等。
塑性指标：拉伸率δ和断面收缩率Ψ。 概 念： 金属在破坏前产生的最大
变形程度，即极限变形量。
H0 - Hk
塑性指标ε= ------------- ×100%（压缩法）
H0
塑性指标衡量金属塑性高低的指标。 塑性状态图及其应用 概念：表示金属塑性指标与变形温度及加载方式的关系曲线图形，简称塑性图。 应用：合理选择加工方法
静态回复 动态回复——主要通过位错的攀移、交滑移来实现。 2.再结晶
静态再结晶：利用金属变形余热发生 动态再结晶：热塑性变形过程中发生 亚动态再结晶：动态再结晶晶粒在热变形停止后的长大过程 (二)热塑性变形后金属组织和性能的变化 1.改善铸造组织，锻合内部缺陷 2.形成纤维组织 3 产生带状组织 超塑性的分类：恒温超塑性或第一类超塑性。
提高塑性的主要途径有以下几个方面： (1)控制化学成分、改善组织结构，提高材料的成分和组织的均匀性； (2)采用合适的变形温度—速度制度； (3)选用三向压应力较强的变形过程，减小变形的不均匀性，尽量造成均匀的变形状态； (4)避免加热和加工时周围介质的不良影响
第二节 金属的流动及其影响因素
第三节 金属塑性成形中的摩擦和润滑
几个基本概念 弹性(Elasticity)：卸载后变形可以恢复特性，可逆性。 塑性(Plasticity)：固体金属在外力作用下能稳定地产生永久变形而不破坏其完整 性的能力 屈服(Yielding)：开始产生塑性变形的临界状态 损伤(Damage)：材料内部缺陷产生及发展的过程 断裂(Fracture)：宏观裂纹产生、扩展到变形体破断的过程
一般讲，如果变形速度大，有没有足够时间完成塑性变形，金属的变形抗力会提高，塑 性降低。变形速度对塑性的影响概括为变形速度的增大，金属和合金的变形抗力提高； 随变形速度提高，塑性变化的一般趋势如图；变形速度对锻压工艺也有广泛的影响。

莫尔应力圆公式推导

莫尔应力圆公式推导莫尔应力圆是材料力学和土力学中一个非常重要的概念，对于理解材料或土体在复杂应力状态下的强度和变形特性具有关键作用。

接下来咱们就一起好好推导一下这个莫尔应力圆公式。

先来说说啥是莫尔应力圆。

想象一下，咱们有一个物体，它内部各个点都受到不同方向和大小的力，这些力综合起来就形成了复杂的应力状态。

莫尔应力圆就是一种能把这种复杂应力状态直观表示出来的工具。

咱从最基础的开始，假设一个平面内有两个互相垂直的主应力，分别是σ₁和σ₃（σ₁ > σ₃）。

还有一个与主应力方向夹角为α 的斜截面上的正应力σ 和剪应力τ 。

根据应力平衡原理，能得到正应力σ 的表达式：σ = (σ₁ + σ₃) / 2 + (σ₁ - σ₃) / 2 × cos 2α 。

剪应力τ 的表达式是：τ = (σ₁ - σ₃) / 2 × sin 2α 。

为了方便推导莫尔应力圆，咱们把上面两个式子变形一下。

令 x =σ ，y = τ 。

先把正应力的式子变形：σ - (σ₁ + σ₃) / 2 = (σ₁ - σ₃) / 2 × cos 2α 。

然后两边平方：[σ - (σ₁ + σ₃) / 2]² = [(σ₁ - σ₃) / 2 × cos 2α]² 。

再把剪应力的式子变形：τ / [(σ₁ - σ₃) / 2] = sin 2α 。

两边平方：τ² / [(σ₁ - σ₃)² / 4] = sin² 2α 。

因为cos² 2α + sin² 2α = 1 ，所以把上面两个平方后的式子相加：[σ - (σ₁ + σ₃) / 2]² + τ² / [(σ₁ - σ₃)² / 4] = 1 。

整理一下，就得到了莫尔应力圆的方程：(x - (σ₁ + σ₃) / 2)² + y² = [(σ₁ - σ₃) / 2]²。

2-弹塑性力学-应力分析


第二章 应力分析 (Stress Analysis)
应力的坐标变换(例题讲解) 应力的坐标变换(例题讲解)*
实际应用:晶体取向, 实际应用:晶体取向,织构分析等
应力莫尔圆**: 应力莫尔圆 :
二维应力莫尔圆与三维应力莫尔圆 掌握如何画,如何分析(工程力学已学,看书) 掌握如何画,如何分析(工程力学已学,看书)
不计体力) (不计体力)
物理意义:表示变形体内无限相邻两质点的点的应力状态的关系. 物理意义:表示变形体内无限相邻两质点的点的应力状态的关系. 对弹性变形和塑性变形均适用. 对弹性变形和塑性变形均适用.
第二章 应力分析 (Stress Analysis)
推导原理:
– 静力平衡条件: 静力平衡条件: –
第二章 应力分析 (Stress Analysis)
八面体应力的求解思路: 八面体应力的求解思路:
σij (i, j = x, y, z) →σ1,σ2 ,σ3 →σ8,τ8
↓→I1,I2 →↑
因为
2 2 τ8 = (I1 3I2 ) 3
第二章 应力分析 (Stress Analysis)
等效应力( 2.6 等效应力(equivalent stress) )
通常规定: 通常规定:
σ1 ≥ σ 2 ≥ σ3
τ max = σ1 σ 3
2
则有最大剪应力:
或者: 或者: 其中: 其中: 且有:
τ max = max{ 12 , τ 23 , τ31 } τ τ12 = ± σ1 σ 2
2 ,τ 23 = ±
σ 2 σ 3
2
,τ31 = ±
σ3 σ1
2
τ12 +τ 23 +τ31 = 0

材料成型原理——主切应力及八面体应力


+σ3 )2 2 +σ1 )2 2
+τ 2 +τ 2
=
l
2
(σ1
−
σ
2
)(σ1
−
σ
3
)
+
σ (
2
− 2
σ
3
)2
=
m2
(σ
2
−
σ
3
)(σ
2
−
σ1)
+
σ (
3
− 2
σ1
)2
⎫ ⎪ ⎪ ⎪ ⎬ ⎪
(σ
−
σ1
+σ2 2
)2
+τ
2
=
n2 (σ 3
− σ1)(σ 3
−σ2)
+
(σ1
−σ2 2
)2
⎪ ⎪⎭
1圆外 2圆内 3圆外
第十一章 应力与应变理论
第三讲 主切应力及八面体应力
阎昱
一、主切应力
1. 复习主应力、主平面的概念
z 主平面： τ = 0 的微分面 z 主应力：主平面上作用的正应力
z 主切应力平面：切应力τ达到极值的微分面
z 主切应力：主切应力平面上作用的切应力
一、主切应力
求解切应力极值
l = 0, m = ±1 2 , n = ±1 2
四、应力平衡微分方程
一点的应力状态
各点的应力变化关系 ？
应力是坐标的连续函数，即 σij = f (x, y, z)
在直角坐标系中，点Q (x,y,z)的应力状态为σij。
无限邻近处点Q′((x+dx),(y+dy),(z+dz))的应力状态为

02讲-应力与平衡、位移与应变

2022/2/8
王正伟 13601363209
9
斜面应力公式 Cauchy Formula
四面体平衡条件为：
(1) dS1 (2) dS2 (3) dS3
()
dS
f
(1dhdS) 3
0
1 xi xy j xzk 2 yxi y j yzk 3 zxi zy j zk
刚体位移和变形是同时出现的 ，在弹性力学中我们忽略刚体运动 对物体的影响，仅考虑变形。
2022/2/8
王正伟 13601363209
23
位移的描述 Characterization of Displacement
拉格朗日坐标系其坐标系是放在所描述的物
体上随着物体一起运动。 拉格朗日描述法以物体变形前的初始构形为参照构
1 xxi xy j xzk
2 yxi yy j yzk
3 zxi zy j zzk
xx yx
xy yy
xz yz
zx zy zz
王正伟 13601363209
6
面力、应力矢量与应力状态辨析
相同点： 量纲相同； 内力与应力的数学定义相同。
S 0
F S
若取 S 为变形前面元的初始面积，则上式给出工程应力，亦称 名义应力，常用于小变形情况。 对于大变形问题，应取 S 为变形后面元的实际面积，称真实应 力，简称真应力, 也称柯西应力。
2022/2/8
王正伟 13601363209
4
应力矢量(应力) Stress Vector
下图为低碳钢轴向拉伸变形情况，前两个图为小变形情况，应 力计算采用工程应力，第三个真实截面面积相比于初始情况变 化剧烈，因而必须采用真实应力来描述。在以后的讨论中主要 研究小变形问题，因而应力计算上为工程应力。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 2!
f
''(x0 )(x x0 )2
x
应力平衡微分方程
➢由于单元体处于平衡状态
Fx 0
( x
x
x
dx)dydz
xdydz
( yx
yx
y
dy)dxdz
yxdxdz
( zx
zx
z
dz)dxdz
zxdxdz
0
x yx zx 0
x y z
应力平衡微分方程
同理，得平衡微分方程
x
x
xy
x
yx
y
y
y
zx
z
zy
z
0
0
xz
x
yz
y
z
z
0
即每个面上在x方向的应力对所在面偏导之和或一 个方向所有应力对各自所在平面求偏导的和为0。
简记为
ij 0
xi
应力平衡微分方程
➢轴对称问题的平衡微分方程
z
dq
dq dr
r
r qrr
q
q
drqz
rz zr
rz
dzrz
莫尔圆上对应的是从相应的坐标点顺（逆）时旋
转2 处的点的坐标。
三向应力莫尔圆
对于三向应力状态，设变形体中某点的 三个主应力为 ， 1 2 ， 3 且 1 〉 2 〉 3 ， 三向应力莫尔圆为：
圆心的坐标和半径分别为：
三个圆的半径分别等于三个主切应力
三向应力莫尔圆
三个圆的方程为
每一个圆分别表示某方向余弦为零的斜面上的正 应力和切应力的变化规律。
第二章 金属塑性变形的力学基础
应力分析
河南科技大学材料学院
平面应力状态下的应力莫尔圆
➢若已知平面应力状态的三个应力分量 z xz yz 0，如何
求任意斜微分面AC上的正应力σ和切应力τ？
AC面的方向余弦
l cos
m cos sin 2
n cos 0 2
对于AC面 Sx xl xym x cos xy sin Sy xyl ym xy cos y sin
Sxm S yl ( xl yxm)m ( xyl ym)l
( x y )sin cos xy (sin2 cos2 )
x
2
y
sin
2
xy
cos 2
Sxl S ym x cos2 y sin 2 2 xy sin cos
x 2
(1
c os 2 )
应力平衡微分方程
➢应力分量是坐标的 连续函数。 ➢Q点: 坐标x，y，z， 应 力状态σij 。过Q点x面上的 正应力 x f (x, y, z)
➢Q′点: 坐标x+dx,y+dy,
zQ+′d点z,x应面力上状的态正σ应ij+力dσij。过y
x d x f (x dx, y, z)
f
(x, y, z) f dx x
10 0 10
ij
0
10
0
10 0 10
7 4 ij 4 1
0
0
（单位MPa）
0 0 4
1）画出该点的应力单元体；
2）求出该点的应力张量不变量、主应力、主 方向、主切应力、最大切应力、等效应力、应 力偏张量及应力球张量。
3）画出该点的应力莫尔圆，并将应力单元体 的微分面分别标注在应力莫尔圆上。
1 2 f 2 x2
dx2
dz
x
x x
dx
z
z z
dz
zx
yx
zx z
xz
dz
xy
xz x
zy
zy z
dz
Q′
x
xz
dx
yz
yz y
y
dy
y y
dy
yz Q
xy
xy x
dx
x
x
zy x
dx
zx
yx
yx y
dy
dx
z
dy
z
y
泰勒级数
f
(x) fFra bibliotek(x0 )
f
'(x0 )(x x0 )
y 2
(1
c os 2 )
xy
sin
2
x
2
y
x
2
y
cos2
xy
sin
2
x
y
2
2
2
x
y
2
2
xy2
平面应力状态下的应力莫尔圆
➢主应力
1 2
x
2
y
x
2
y
2
2 xy
3 0
➢主应力σ1与x轴之间的夹角
1 arctan 2 xy
2
x y
➢从某一平面顺（逆）转 的任意斜面上应力在
r
dr
rq
rq
r
dr
z
q
r
r
r
dr
z
dz
o
y
q
r
x
应力平衡微分方程
➢轴对称问题的平衡微分方程
r 1 qr zr r q 0
r r q z
r
rq 1 q zq 2 rq 0 r r q z r
rz 1 q z z rz 0 r r q z r
作业
1. 对于Oxyz直角坐标系，已知受力物体内一点的 应力状态为