当前位置：文档之家 › 5.2 简谐振动的旋转矢量表示法

5.2 简谐振动的旋转矢量表示法

  • 格式：ppt
  • 大小：1.91 MB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

大学物理简谐振动

大学物理简谐振动
tan A1 sin 1 A2 sin 2 A1 cos1 A2 cos2
A2
A
A2 sin 2
2 -1
2
O
1 A1 x2
A1 sin 1
x2 x
x1x1
x2
x
A1 cos1 A2 cos2
合振动振幅：A A12 A22 2A1A2 cos(2 1)
1. 两个分振动的相位相同（同相）
5 (或 3 )
4
4
第六章
机械波
mechanical wave
6.1 机械波的产生、传播和描述 波动: 振动在空间中的传播过程.
机械波: 机械振动在弹性介质中的传播过程. 波动
电磁波: 交变电磁场在空间中的传播过程. 6.1.1 机械波的产生
当弹性介质中的一部分发生振动时，由于介质各个 部分之间的弹性力作用，振动就由近及远地传播出去. (1) 机械波实质上是介质中大量质点参与的集体振动;
20 0.47
(2) 30为何值时, x1+x3 的振幅为最大; 30为何值时, x2+x3的振幅为最小.
x1 0.05cos10t 3 4
x2 0.06cos10t 4
x3 0.07 cos10t 30
30
10
0 时，x1+x3 振幅最大：30
10
3
4
30 20 时，x2+x3 振幅最小：30 20
t 时刻点 P 的振动状态
P点在
t
时刻的位移
y P ,t
yO ,t x
u
A c os [ (t
x) u
0 ]
波函数 (波方程)
y( x, t )
A cos[ (t

大学物理B(Ⅱ)旋转矢量

大学物理B(Ⅱ)旋转矢量
2
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示，求振动周
期.
t(s) t 0

A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ，求 1）如图简谐运动方
A＇
44
因为 v0 0 ，由旋转矢量图可知 ＇ π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动，其振
幅为 0.08m，周期为 4s ，起始时刻物体在 x 0.04m
处，向 Ox轴负方向运动（如图）.试求
（1）t 1.0s 时，物体所处的位置和所受的力；
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m

简谐运动的旋转矢量描述法

简谐运动的旋转矢量描述法

π
4
A g a'*
h' * g'* *
t f O b*' T T f'* 3T T 5T
e
c' 4* 2*e' 4
4
-A
d*'
T 2 （旋转矢量旋转一周所需的时间）
用旋转矢量图画简谐运动的 x t 图
T 2π （旋转矢量旋转一周所需的时间）
二、旋转矢量法对相位的表示
若某时刻t，测得质点的位移为x =A/2，向OX轴负方
简谐运动的旋转 矢量表示法
一、简谐运动的旋转矢量表示法
P
t=t
t+
o
A t=0
A
x·
x
x Aco（s t ）
x Aco（s t ）
旋 转 矢量 A的
x 端点在
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
用旋转矢量图画简谐运动的 x t 图
x
Ah
a
bO
c -Ad
x
x Acos(t )
向运动
M
A
O 3P
X
M
三、旋转矢量法对相位差的表示
A2
A1
O
相位差 2 1 2kπ
x
(k 0，1， 2,)
两个振动同相，步调相同
A1
O
A2
相位差 2 1 (2k 1)π
x
(k 0，1,)
两个振动反相，步调相反
例题 两个同方向、同频率的谐振动，频率为2s-1，
当第一个振子从平衡位置向正向运振动的相位差。
解：
2 1
A 2
t
o

简谐振动-旋转矢量法

简谐振动-旋转矢量法

sin2 (2 1)
y
2） 2 1 π
y A2 x A1
3）2 1 π 2
x A2
o A1
x2 A12
பைடு நூலகம்
y2 A22
1
x A1 cost
y
A2
cos(t
π) 2
A2 y
o A1 x
用 旋 转 矢 量 描 绘 振 动 合 成 图
两
相
互 垂 直 同 频 率 不 同 相
简 谐 运 动 的 合 成 图
x
x
A1 o
o
A
A2
A A1 A2
Tt
结论
A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相位：
2 1 2k k 0,1, 2,
A A1 A2
若两分振动反相位:
两分振动相互加强
2 1 (2k 1) k 0,1, 2,
A A1 A2
两分振动相互减弱
再若 A1= A2 , 则 A= 0
M
A
P
x
注意：旋转矢量在第 2 象限
速度v <0
M
PA
x
注意：旋转矢量在第 2 象限
速度v <0
M
PA
x
<
注意：旋转矢量在第 3 象限
速度v 0
P x
MA
<
注意：旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意：旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意：旋转矢量在第 3 象限
速度v 0
找到谐振动的特征量，问题就解决了。

简谐运动及其旋转矢量表示法简谐运动的能量讲课文档

简谐运动及其旋转矢量表示法简谐运动的能量讲课文档
简谐运动及其旋转矢量表示法简谐运动的能量
现在一页，总共十五页。
9.1 简谐振动
一、弹簧振子 1. 受力特点
线性恢复力 F kx
2. 运动方程
据牛顿第二定律得：
若令 ω k m
kx
m
d2 dt
x
2
上式改写为
d2 dt
x
2
2
x
0
解得 x(t) Acos(ω t )
现在二页，总共十五页。
二、简谐振动
x
现在十三页，总共十五页。
2. 同相和反相
x
A1
x1
A2
x2
T
o
- A2
t
-A1
= 2n
两运动步调相同, 称同相
A2
A1
x
A1
x1
A2
T
o
- A2
x2
t
-A1
= (2n+1)
两运动步调相反 ,称反相
A2
O
x
O
x
A1
现在十四页，总共十五页。
例 如图所示，一质点作简谐振动，在一个周期内先后通过距
相位反映了物 体某一时刻的
运动状态
现在三页，总共十五页。
3. 由初始条件求振幅和初相位
熟练掌握
x0 v0
x Acos(ω t ) v ω Asin(ω t )
初位移 x0 Acos 初速度 v0 ω Asin
A
x02
v
2 0
2
tan1( v0 ) x0
注意: 确定 的象限
现在四页，总共十五页。
逆时针旋转 。其端点在
x 轴上的投影
点的运动为 简谐运动， 有：

简谐振动旋转矢量图

简谐振动旋转矢量图

2
T
t
)
8
例1：一个沿 x 轴作谐振动的弹簧振子，振幅为
A，周期为T，其振动方程用余弦函数表示。若 t
= 0 时，质点的状态分别为：（1）x0=－A；试 求相应的初相，并写出振动方程。
解： x
A cos( t
)
Acos( 2
T
t
)
（1）解析法（x0=－A）
由x0 Acos A， cos 1， ＝
7
例1：一个沿 x 轴作谐振动的弹簧振子，振 幅为 A，周期为T，若 t = 0 时，质点的状 态分别为：（1）x0=－A；（2）过平衡位 置向x正向运动；（3）过 x = A/2 处向x负 方向运动；试求相应的初相，并写出用余 弦函数表示的振动方程。
解：所求振动方程为
x
A cos( t
)
A
cos(
下落： v 2gh
碰撞：mv (m M )v0 t 0, y0 (2 1 )
A
y02
v02
2
arctan(
,
v0
y0
),
(2)
1
y
2
O
h
A
cos(
2
T
t
y
)
16
本节课小结： （1）A,ω, 的确定。 （2）掌握旋转矢量法。 作业：7-5
17
T
t
3
)
11
例2：画出质点处于①平衡位置且速度小于 零，②正最大位移，③(1/2)位移处且速度 为正值的旋转矢量,说明初相的大小并画出 振动曲线。
解：①
xx
A
0o
2
Tt
12
②正最大位移 x
A

第四章振动下

第四章振动下

结论： 结论：
振子在振动过程中， （1） 振子在振动过程中，动能和势能分别随时间 变化，但任一时刻总机械能保持不变。 变化，但任一时刻总机械能保持不变。 （2） 动能和势能的变化频率是弹簧振子振动频 率的两倍。 频率一定时， （3）频率一定时，谐振动的总能量与振幅的平方 成正比。（适合于任何谐振系统） 。（适合于任何谐振系统 成正比。（适合于任何谐振系统） 弹性势能
小结：
描述简谐振动的三种方法： 描述简谐振动的三种方法： 运动方程，振动曲线，旋转矢量。 运动方程，振动曲线，旋转矢量。
的简谐振动， 例1：一物体沿 轴作振 幅为 A 的简谐振动，若初始时该球的 ：一物体沿x轴作振 状态为（ ） ；（2）在平衡位置且向X轴正方向运动 轴正方向运动； 状态为（1）X0＝ -A；（ ）在平衡位置且向 轴正方向运动； ；（ 处向X轴负方向运动；（4） 轴负方向运动；（ （3）在 X0＝1／2 A 处向 轴负方向运动；（ ）在 ） ／ 方向运动。试用旋转矢量法确定相应的初相位。 处向正 方向运动。试用旋转矢量法确定相应的初相位。 3π r ϕ = ϕ =π
k = m
得
X
g b
mg
b, v 0 = 0
g t+π) b
A =b, φ = π
[ 例2] 一谐振动的振动曲线如图所示。 一谐振动的振动曲线如图所示。
ω 以及振动方程。 求： ϕ 0 以及振动方程。
−
π
x
x
A 2
3r
A
1.0
0
解：
t
r A
A
π
2
x
π
3
t=
A x0 = = A cos ϕ 0 2 0时 v 0 = − ω A sin ϕ 0 > 0

简谐振动的旋转矢量图示.ppt

简谐振动的旋转矢量图示.ppt

角频率ω
A 与参考方向x 的夹角
振动相位ωt+φ0
3、两个谐振动的相位差
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
相位差为 (t 2 ) (t 1) 2 1
采用旋转矢量表示为：
A2
2
A1
1
O
x
例1、两个同频率的谐振动，它们都沿x轴振动，且振
幅相等，当t =0时质点1在x=A/2处向左运动,另一质点
F kx m 2x
(0.01kg)(π s1)2 (0.069m) 1.70103 N
2
（2）由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
解法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04m (0.08m) cos[(π s1)t π ]
x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
3 a 0.12 2 cos( 0.5 ) 1.03 m/s2
3
在t =T/4=0.5s时，可得
可得x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
sin0 0
0
3
简谐振动表达式 x 0.12cos( t ) m
3
因为
（2）由简谐振动的运动方程 x 0.12cos( t ) m
3
可得
v dx 0.12 sin( t ) m/s
dt
3
a dv 0.12 2 cos( t ) m/s2

物理-简谐振动的基本特征与旋转矢量图示法

物理-简谐振动的基本特征与旋转矢量图示法

研究简谐振动的重要性
机械振动的分类（从振动形式分） 连续振动、非连续振动； 周期振动、非周期振动…；
最简单、最基本的振动 —— 简谐运动.
简谐运动
合成 分解
复杂振动
机械振动第一讲
简谐振动的基本特征 旋转矢量图示法
一、简谐振动的定义
简谐振动
物体运动过程中，如果离开平衡位置的位 移（或角位移）按余弦函数（或正弦函数） 的规律随时间变化的运动，称为简谐振动。
三、简谐振动的三个特征量
4、振幅(A)与初相()的确定
设
注意 应根据
的符号确定 的象限范围。
三、简谐振动的三个特征量
讨论：两个同频谐振动的振动步调关系
谐振动1 x1 A1 cos(t 1 )
谐振动2 x2 A2 cos(t 2 )
相位差 (t 2 ) (t 1) 2 1
x
1）若 2 1 0
2
x轴负方向运动，而质点2在-A处。
试用旋转矢量法求这两个谐振动的初相差，及 两个质点第一次通过平衡位置的时刻。
四、简谐振动的旋转矢量图示法
小结：用旋转矢量法求相位或相位差的
O
x
第一步：由质点的位移x的值确定旋转矢量动端投影点 在x轴上的位置；
第二步：过该点作x轴的垂线，与矢量参考圆交于两点； 第三步：由质点振动速度的方向确定旋转矢量的位置。
运动学方程： 2、圆频率（ω）
最小正周期
完成一次全振动所需的时间
振动周期
振动频率 （系统固有）
三、简谐振动的三个特征量
运动学方程：
3、初相（ ）
振动速度 振动加速度
若A与确定：物体在t时刻的（x,v,a） 仅由( t + ) 决定。 称( t + ) 为物体在 t 时刻振动的相位(或)。 t =0 时的相位 ——初相位（或初相）

简谐振动的旋转矢量表示法_大学物理（下）_[共2页]

简谐振动的旋转矢量表示法_大学物理（下）_[共2页]

第11章 机械振动 7
（2）求该系统的角频率、振幅和初相。

解：（1）设在空盘静止时，弹簧的伸长量为1l ，即
01g m kl =；物体和盘整个系统达到平衡时，弹簧的伸长
量为2l ，即02()g m m kl +=，同时取该位置为坐标原点O ，
竖直向下为y 轴正向。

某一时刻，振动系统的位移为y 时，所受的力为
02()g ()F m m k y l ky =+-+=-
显然，符合简谐振动的动力学特征，故系统的振动
为简谐振动。

（2）振动系统的角频率为
ω=
对于振幅和初相则由初始条件来决定。

0t =时刻时，021()y l l =--，又01g m kl =，02()g m m kl +=，故初始位置为
0g /y m k =-
物体从h 高度自由下落到盘上，
速度0v ，物体与盘子发生非弹性碰撞，竖直方向动量守恒，即
000()mv m m u =+
则初始速度为
0000m u v m m ==+
代入公式得
A ==
00
arctan()ππu y ϕω-=+= 所以 cos()y A t ωϕ=
+π)=++
注意：初始时刻小球速度方向竖直向下，位移为负值，则初相为第三象限的角度。

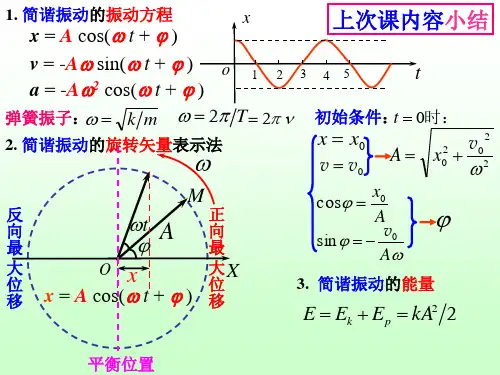
11.2 简谐振动的旋转矢量表示法
前面我们分别用数学表达式法和振动图像来描述简谐振动，下面介绍一种更直观更为方便的描述方法——旋转矢量法。

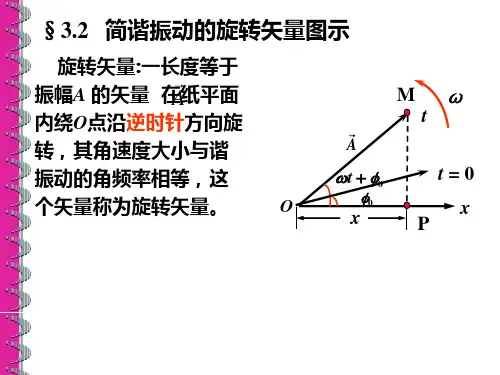
如图11-6所示，在平面内作一坐标轴Ox ，由原点O 作矢量A
，其大小等于简谐振动的振
图11-5 例11-2。

机械振动——简谐运动的基本概念2

机械振动——简谐运动的基本概念2
4．振动的合成(第 6 节内容) 例：一个质点沿 x 轴作简谐运动，振幅 A=0.06m，周期 T=2s，初始时刻质点位 于 x0=0.03m 处且向 x 轴正方向运动。求： （1）初相位； （2）在 x=-0.03m 处且 向向 x 轴负方向运动时物体的速度和加速度以及质点从这一位置回到平衡位置 所需要的最短时间。 解： （1）取平衡位置为坐标原点，质点的运动方程可写为
两边对时间求导，得
1 dv 1 dx m ⋅ 2v + k ⋅ 2 x =0 2 dt 2 dt
即
m⋅v
d 2x + k ⋅ xv = 0 dt 2 d 2x k + x=0 dt 2 m
令ω ＝
2
k ，则 m d 2x +ω2x = 0 2 dt
其解为
x = A′ cos(ωt + ϕ )
代入守恒方程可得 A=A’ 例 2．劲度系数为 k、原长为 l、质量为 m 的匀质弹簧，一端固定，另一端系一 质量为 M 的物体，在光滑的水平面上作直线运动，求其运动方程。
v A＝ x + 0 ω
2 0
2
二、能量平均值 定义：一个随时间变化的物理量 f(t)，在时间 T 内的平均值定义为
114
机械振动——简谐振动的基本概念
f =
1 f (t )dt T∫ 0 1 1 1 1 2 2 2 2 2 2 ∫ 2 mA ω sin (ωt + ϕ )dt = 4 mA ω = 4 kA T 0 1 1 2 1 2 1 2 2 2 ∫ 2 kA cos (ωt + ϕ )dt = 4 kA = 4 mA ω T 0
113
机械振动——简谐振动的基本概念
简谐运动的能量

5-2旋转矢量

5-2旋转矢量

0
5–2 旋转矢量 二. 旋转矢量法的应用：
第五章 机械振动
关键：正确判断初始时刻 的位置和速度的正负！！
1. 简便确定初相或相位

M
A
A 例如： t 0 : x0 , v0 0 2
求初相
o
A
x0
x

M
5 或 3 3

5–2 旋转矢量
第五章 机械振动
2. 快速准确画出简谐运动的振动曲线
相位差 2
3
x/m
(t2 ) (t1 )
求
或 t
1
t
6

t/s
t=0
t=4s
x0 3
v0 0
0
4
x0
v0
2 2
t=4s
4 , 6
1 (s ) t 6
-A
A 2 o 1
A＇
P141 5-2
5–2 旋转矢量 例2 一谐振动的振动曲线如图所示 求(1)振动方程 A
第五章 机械振动
v0 *P
0
x
(2)到达P点位置的时间.
2
A
1.0
t/s
解(1)
v0 0 3 t=1.0s A x1 0 1 t 1s : 2 v1 0 2 o x 5 5 t 3 A 6 2 3 6 5 t=0 t ) 振动方程为 x A cos( 6 3
A 0.05m
6.0s 1
0
A cos(t ) A cos(t ) v A sin t
A
t
A x 2
π 由旋转矢量图可知 t 3

5-2 旋转矢量

5-2 旋转矢量

20 10 0 , 20 10
表示 x2 振动超前 x1 振动Δφ。
20 10 0 , 20 10
表示 x2 振动滞后 x1 振动Δφ。
x
2 超前于1 或 1滞后于 2
4）研究简谐振动位移、速度、加速度之间的相位关系
x A cos( t 0 ) p v A sin( t 0 ) v m cos( t 0 ) 2 2 a A cos( t 0 ) am cos( t 0 p )

π
t 3
o
π 3
0.04 0.08
x/m
π 1 s 2 t 0.667 s
π t 3
0.08 0.04
5 – 2 旋转矢量 补充例题 一质点沿x轴作简谐振动，振幅A＝0.05m， 周期 T＝0.2s。当质点正越过平衡位置向负 x 方向时开 始计时。 （1）写出此质点的简谐运动的表达式； （2）求在 t＝0.05s 时质点的位置、速度和加速度； （3）另一质点和此质点的振动频率相同，但振幅为 0.08m，并和此质点反相，写出另一质点的简谐运动表 达式； （4）画出两振动的相量图 解： x
T/4 T/4
x a o
T t

vm
r A
900 900
am
t+

x
v
0 0
r r p 由图可见： v 超前 x 2
o
·

r r p a 超前 v 2
例1 如图所示，一轻弹簧的右端连着一物体，弹簧的劲度系 1 数 k 0.72N m，物体的质量 m 20g . （1）把物体从平衡位置向右拉到 x 0.05 m 处停下后再释放， 求简谐运动方程； （2）求物体从初位置运动到第一次经过

5-2旋转矢量

5-2旋转矢量

2
5-2 旋转矢量
第五章 机械振动
一 用旋转矢量表示简谐运动 以 o为
v A
ω
ωt + ϕ 0 ϕ0
v 量 A的端点
原点旋转矢 在
v A
x 轴上的
投影点的运 动为简谐运 动. 当
o x
x
t = t 时 x = A cos(ωt + ϕ 0 )
3
5-2 旋转矢量
第五章 机械振动
一 用旋转矢量表示简谐运动
t = 0, x0 = 0.04m
A
π 3
− 0.08 − 0.04
ω
x/m
20
o
v
0.04 0.08
5-2 旋转矢量
第五章 机械振动
π π x = 0.08cos( t + ) (m) 2 3
t =1.0s
x = −0.069m k F = −kx ω= 2 m = −mω x −3 m = 0.01kg =1.70×10 (N)
x = A cos( ω t + ϕ 0 )
v 矢量 A 的
端点在 轴上的投 影点的运 动为简谐 运动. 运动.
旋转
x
4
5-2 旋转矢量
第五章 机械振动
播放教学片 CD2 旋转矢量 5′13″
5
5-2 旋转矢量
第五章 机械振动
一 用旋转矢量表示简谐运动
v y vm
ωt + ϕ 0
v an
0
π ωt +ϕ0 + 2
′ Qv′ = −A′ω sin ϕ0 > 0 0 π 或用矢量图可得 ∴ϕ＇ − = 4
π x = 0.07 cos(6t − ) (m) 4

4.2 简谐振动的旋转矢量表示法

4.2 简谐振动的旋转矢量表示法

二、两个简谐振动的比较 相位差
x1 = A cos(ωt + φ1 ) 振幅和角频率相同） （振幅和角频率相同） x 2 = A cos(ωt + φ2 )
两个同频率简谐振动的相位差（ 两个同频率简谐振动的相位差（几个说 法）: (ωt + φ2 ) − (ωt + φ1 ) = φ2 − φ1 >0 x2超前 1 超前x x2落后 1 落后x 反相 同相
1 t= 2
ϕ2 −ϕ1 <0 =(2k±1)π ± =2kπ
轴作简谐振动，振动方程为: 例：一质点沿 x轴作简谐振动，振动方程为
x = 4×10−2 cos(2πt +π / 3) 时刻起， 从 t = 0时刻起，到质点位置在 x = −2cm处，且 向 x轴正方向运动的最短时间间隔为
A
ϕ=
π
3
ω
X
π = ωt = 2πt
一、简谐振动的旋转矢量表示法
ω
t
ωt φ O
A
t=0
x
x = A cos(ωt + φ )
x = A cosφ
可见当旋转矢量A作匀角速度旋转时， 可见当旋转矢量 作匀角速度旋转时，其端点 作匀角速度旋转时 轴的投影点的运动与振动的规律相同。 在Ox轴的投影点的运动与振动的规律相同。所以 轴的投影点的运动与振动的规律相同 每一个简谐振动都可以用旋转矢量来表示
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

π v A cos( t ) 2
a A cos(t )
2
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
用旋转矢量图画简谐振动的

x
A
x
A
*
x A cos(t )
*
T * 3T 2 4
x t
*
* T
图
π 4

O -A
O * T
4
*
-A
*
x1 A1 cos(t 1 )
x2 A2 cos(t 2 )
2 1
为其它
(t 2 ) (t 1 )
0 同步
π 反相
超前 落后
x
x
x
o
t
o
t
o
t
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
例 一放置在水平桌面上的弹簧振子，振幅 ， 2 A 1.0 10 m ，周期 T 1 s。当 t 0 时，试分别 振幅 写出以下两种初始条件下简谐振动的运动学方程。（ 1） 3 x0 5.0 10 m x轴负方向运动；（2） 质点位于 处，向 3 x0 5.0 10 m x轴正方向运动。 质点位于 处，向 ，且v0 ＜0，可得旋转矢量的初始位置如 图（a）所示。由图（a）可得简 谐振动的初相位 。由此 3 及 2 / T 2 rad / s，A 1.0 102 m， 可得简谐振动运动学方程为

A
o
v A sin t
A 2
x
0.26m s
1
（负号表示速度沿 Ox 轴负方向）
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
（3）如果物体在 x 0.05 m 处时速度不等于零， 1 而是具有向右的初速度 v0 0.30m s ，求其运动方程 . 解 A＇
x0 解 （1）t 0 时， A 2

A O v0 x0 a)
3
x0v0
4 3
x
A
O
x

b)
x 1.0 102 cos(2 t ) m 3
第5章 机械振动

5.2 简谐振动的旋转矢量表示法
量的初始位置如图（b）所示。由图（b）可得振动 4 2 初相位 或 。因此，简谐振动运动学方程 3 3 为 2 2 x 1.0 10 cos(2 t )m 3
量 A的端点
在
o
x0 A cos
x0
x
x 轴上的
投影点的运 动为简谐运 动.
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
2π T
A M
t t
时

M0
以 o为 原点旋转矢
t
量 A的端点
在
o
x
x0
x
x 轴上的
投影点的运 动为简谐运 动.
第5章 机械振动
x A cos(t )

A O v0 x0 a)
3
4 x0v0 3
A （2）根据题意，x0 2 ，且 v0 >0，可得旋转矢
x
A
O
x

b)
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
例 如图所示，一轻弹簧的右端连着一物体，弹簧 1 的劲度系数 k 0.72N m ，物体的质量 m 20g .
*
5T 4
t
T 2π （旋转矢量旋转一周所需的时间）
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
用旋转矢量图画简谐振动的
x t
图
T 2π （旋转矢量旋转一周所需的时间）
第5章 机械振动
5.2 简谐振动的旋转矢量表示法 讨论
相位差：表示两个相位之差 . 1）对同一简谐振动，相位差可以给出两运动状 态间变化所需的时间. (t 2 ) (t1 )
5.2 简谐振动的旋转矢量表示法
简谐振动的规律除了用简谐振动的运动学 方程和振动曲线表示外，还可以采用旋转矢量 表示法。 旋转矢量表示法可以更直观地说明简谐振动 运动学方程中各个特征物理量的意义。
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
2π T
当

t 0时

A M
0
以 o为 原点旋转矢
解
A 0.08 m
2π π 1 s T 2
第5章 机械振动
t 0, x 0.04m
π v0 0 3
5.2 简谐振动的旋转矢量表示法 2π π 1 A 0.08 m s T 2
代入 x
0.04 0.08cos
A cos(t ) π 3
由旋转矢量图可知
第5章 机械振动
5.2 简谐振动的旋转矢量表示法 A （2）求物体从初位置运动到第一次经过 处时的 2 速度；
解
x A cos(t ) A cos(t )
A
x 1 cos( t ) A 2 π 5π t 或 3 3 π 由旋转矢量图可知 t 3
x
A
A2
x A cos(t1 ) x A cos(t2 )
t t 2 t1

a
b
π 3
Ab

o
A
v
t
A
0 A


x
π 3 1 t T T 2π 6
2
Aa A
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
2）对于两个同频率的简谐振动，相位差表示它 们间步调上的差异.（解决振动合成问题）
（1）把物体从平衡位置向右拉到 x 0.05 m 处停 下后再释放，求简谐振动方程； A （2）求物体从初位置运动到第一次经过 处时的 2 速度； （3）如果物体在 x 0.05 m 处时速度不等于零， 1 而是具有向右的初速度 v0 0.30m s ，求其运动方程 .
x/m
o
0.05
A
π 3

0.08 0.04
0.04 π x 0.08 cos( t 2
o
x/m
0.08 π ) 3
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
m 0.01kg
0.08 0.04
v
o
0.04 0.08
x/m
π π x 0.08 cos( t ) 2 3
t 1.0s 代入上式得
5.2 简谐振动的旋转矢量表示法
例 一质量为 0.01kg的物体作简谐振动，其振 幅为 0.08 m ，周期为 4s ，起始时刻物体在 x 0.04 m 处，向 Ox 轴负方向运动（如图）.试求 （1 ） t
1.0s
时，物体所处的位置和所受的力；
v
0.08 0.04
o
x/m
0.04 0.08
5.2 简谐振动的旋转矢量表示法
x A cos(t )
矢量 A的
端点在 轴上的投 影点的运
旋转
x
动为简谐
运动.
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
y vm
t
0
an
π t 2
A
vm A
v a

x
an A
2
x A cos(t )
2
x 0.069 m
F kx m x 1.70 103 N
第5章 机械振动
5.2 简谐振动的旋转矢量表示法 （2）由起始位置运动到 x 0.04 m 处所需要
的最短时间.
v
0.08 0.04
o
x/m
0.04 0.08
解法一 设由起始位置运动到 x 0.04 m 处 所需要的最短时间为 t
π π 0.04 0.08 cos( t ) 2 3
t 0.667 s
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
解法二
Hale Waihona Puke t时刻π 3
t
o
起始时刻
π 3
0.04 0.08
x/m
0.08 0.04
π t 3
π 1 s 2
t 0.667 s
第5章 机械振动
第5章 机械振动
5.2 简谐振动的旋转矢量表示法
k 0.72N m 解 （ 1） m 0.02kg
1
6.0s 1
v A x x0 0.05m v0 tan 0 x0 0 或 π
2 0
2 0 2
o
A
x
0 x A cos(t ) 0.05 cos 6.0t m
0 ，由旋转矢量图可知 ＇ π 4 π x A cos(t ) 0.0707 cos( 6.0t )
因为 v 0
v0 tan＇ 1 x0 π 3π ＇ 或 4 4
x
2 0
v
2 0 2
0.0707m
o
π 4
x
A＇
4
第5章 机械振动