当前位置：文档之家 › 简谐振动旋转矢量表示法.ppt

简谐振动旋转矢量表示法.ppt

  • 格式：ppt
  • 大小：688.50 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

大学物理B(Ⅱ)旋转矢量

大学物理B(Ⅱ)旋转矢量
2
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示，求振动周
期.
t(s) t 0

A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ，求 1）如图简谐运动方
A＇
44
因为 v0 0 ，由旋转矢量图可知 ＇ π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动，其振
幅为 0.08m，周期为 4s ，起始时刻物体在 x 0.04m
处，向 Ox轴负方向运动（如图）.试求
（1）t 1.0s 时，物体所处的位置和所受的力；
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m

简谐振动的动力学特征及运动学-PPT

简谐振动的动力学特征及运动学-PPT

• 动力学方程
d2 dt
x
2
2
x
0
9
§4-1 简谐振动的动力学特征
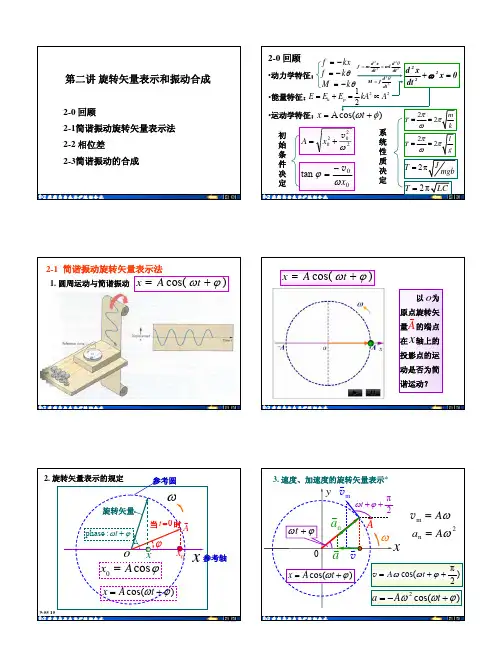
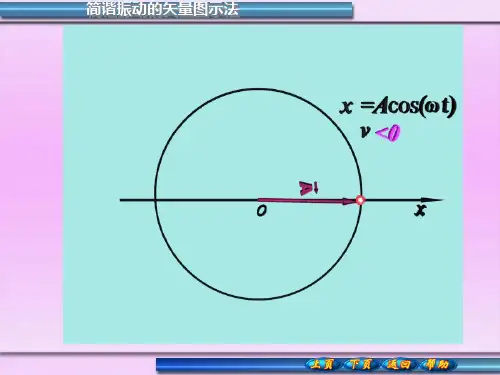
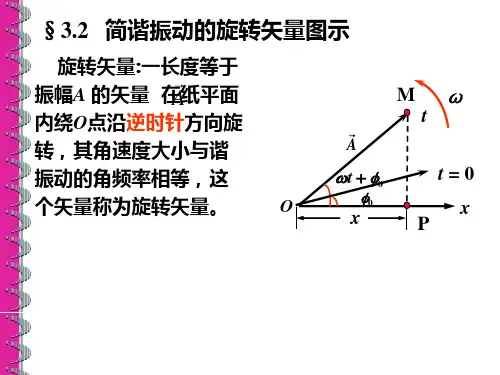
x Acos(t )
T 2π 取 0
x xt图
A
o
T
A
v vt 图
t
v A sin(t ) A
o
Tt
A cos(t π ) A
2
a a t图
a A 2 cos(t ) A 2
o
Tt
A 2 cos(t π ) A 2
两振动位相之差
＝2－ 1
•当=2k ,k=0,±1,±2…,两振动步调相同,称同相
•当=(2k+1) , k=0,±1,±2...
两振动步调相反,称反相
•0<<
2 超前于1 或 1滞后于2
位相差反映了两个振动不同程度的参差错落
•谐振动的位移、速度、加速度之间的位相关系
x
A cos( t
A sin(
§4-2 简谐振动的运动学
例题 质点沿x轴作谐振动, 周期T=s, t=0时， xo 2m ,o 2 2m / s,求振动方程。
解： x =Acos( t+ )
2 2
T
A
xo2
o2 2
2
cos 2
2
sin 2
2
3
4
得x 2cos( 2t 3 )m
4 32
dt 2
x Acos(t 0 )
cos(t
0
)
sin(t
0
2
)
令
'
0
2
x Asin(t ' )
简谐振动的运动规律也可用正弦函数表示.

简谐运动的旋转矢量描述法

简谐运动的旋转矢量描述法

π
4
A g a'*
h' * g'* *
t f O b*' T T f'* 3T T 5T
e
c' 4* 2*e' 4
4
-A
d*'
T 2 （旋转矢量旋转一周所需的时间）
用旋转矢量图画简谐运动的 x t 图
T 2π （旋转矢量旋转一周所需的时间）
二、旋转矢量法对相位的表示
若某时刻t，测得质点的位移为x =A/2，向OX轴负方
简谐运动的旋转 矢量表示法
一、简谐运动的旋转矢量表示法
P
t=t
t+
o
A t=0
A
x·
x
x Aco（s t ）
x Aco（s t ）
旋 转 矢量 A的
x 端点在
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
用旋转矢量图画简谐运动的 x t 图
x
Ah
a
bO
c -Ad
x
x Acos(t )
向运动
M
A
O 3P
X
M
三、旋转矢量法对相位差的表示
A2
A1
O
相位差 2 1 2kπ
x
(k 0，1， 2,)
两个振动同相，步调相同
A1
O
A2
相位差 2 1 (2k 1)π
x
(k 0，1,)
两个振动反相，步调相反
例题 两个同方向、同频率的谐振动，频率为2s-1，
当第一个振子从平衡位置向正向运振动的相位差。
解：
2 1
A 2
t
o

02简谐振动的运动学精品PPT课件

02简谐振动的运动学精品PPT课件

19
t t
o
A
t
x
x Acos(t )
点旋以转o矢为量原A
的端点在 x 轴
上的投影点的
运动为简谐运
动.
第4章 机械振动
4–2 简谐振动的运动学
20
y
vm t π
2
t an
A
0
a
v
x
x Acos(t )
vm A v A sin(t )
an A 2
a A 2 cos(t )
雌性蚊子 雄性蚊子 苍蝇 黄蜂
355~415 455~600 330 220
第4章 机械振动
4–2 简谐振动的运动学
例 如图所示系统（细线的质 量和伸长可忽略不计），细线 静止地处于铅直位置，重物位 于O 点时为平衡位置.
若把重物从平衡位置O 略 微移开后放手, 重物就在平衡 位置附近往复的运动．这一振 动系统叫做单摆. 求单摆小角 度振动时的周期．
12
x 简谐运动中， x和 v
间不存在一一对应的关系. A
x A cos(t 0 ) o
v A sin(t 0 ) A
v v
T 2
xt 图
v T t
3、位相和初位相 t 0
1） t 0 (x, v) 存在一一对应的关系;
2）相位在 0 ~ 2π 内变化，质点无相同的运动状态；
相差 2nπ (n为整数 )质点运动状态全同.（周期性）
4–2 简谐振动的运动学
1
一 简谐振动的运动学方程
d2x 2x 0
dt 2
x Acos(t 0 )
cos(t
0
)
sin(t
0
2
)

旋转矢量和振动合成

旋转矢量和振动合成
x = A 2 ,且向x 负向运动。
如：位相ωt2 +φ = 3π 2，问状态？ x =0 ，且向 x 正向运动。
ω
Aπ
3
o
x
例2. 已知状态求位相（特别是初位相）
如：t =0，x0 = A 2，v0>0，求φ ？
φ = 5π 3 或 φ = −π 3
A2
如：t = 0 ，x0 = − A 2 ，v0 <0,求 φ ？ −A 2 o
x/m
x/m
v A2 Δϕ
v A1
0.2
21
0.1
o
1234
56
t/s
解： A = 0.2m
ϕ1
=
−
π 2
T = 4s ω = 2π = π (1/s)
T2
x1
=
π 0.2 cos(
2
t
−
π 2
)
(SI)
Δt
=
Δϕ ω
φ2
=
−
π 3
x2
=
பைடு நூலகம்
π 0.2 cos(
2
t
−
π )
3
(SI)
(
=
π π
6 2
=
1 3
ω
Av
v A3
vϕ3
x ϕ
v
ϕ
A2
2
ϕ1 A1
多个同方向同频率简谐运动合成仍为简谐运动
11:00 10 9-2 旋转矢量表示和振动合成
x1 = A0 cos ω t
x2 = A0 cos( ω t + Δϕ )
xxNL3 ==LAA00ccooss[(ωωt
t +

10-1 简谐振动的矢量图示法

10-1 简谐振动的矢量图示法
简谐振动的矢量图示法
简谐振动的矢量图示法
A 的长度
振幅A
A旋转的角速度
振动圆频率 O
ω
M
A
t 0
P
X
x
A 旋转的方向
逆时针方向
A 与参考方向x 的夹角 振动相位
M 点在 x 轴上投影(P点)的运动规律：
x Acos(t 0 )
矢量OM 的端点 M 所画的圆叫参考圆。 矢量 OM 0 是 t = 0 时刻的位置，它与 x 轴的夹角φ叫初相位。 简谐振动的参考圆和矢量表示方法十分形
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求：ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求：ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
t
=
0时
{
x 0
=
A 2
补例 1一谐振动的振动曲线如图所示
求：ω 、φ 以及振动方程。
x
A 2
A 1.0
解：已知 A = 0.12 m，T = 2s，
ω = 2π/T = π ( rad/s ).
( t =1 s ) B ’
ω
(1) 初态 t = 0 时，
x = 0.06， v ＞0， 初相 φ = －π/3 ,
-0.06
●
O 0.06
●
φ
Δφ
x (m
运动表达式为：
( t = 5/3 s) B
A(t=0)
速度v 0
P
A
x
M

振动力学教程PPT课件

振动力学教程PPT课件

动的叠加-----------谐波分析
•
2、非周期：利用傅立叶积分作谐波分析
• δ函数又称为单位脉冲函数-----它的性质、应用
示成一系列简谐振
第22页/共35页
第一节：简谐振动及其表示方法
•一、简谐振动的表示方法
• （一）正弦函数表示
2、A、ω、Φ ------简谐振动三要素
第23页/共35页
第24页/共35页
船舶的模态分析和强度分析，飞行器的结构振动和声疲劳分析等。
3） 在土木建筑、地质工程中：建筑、桥梁等结构物的模态分析，地震
引起结构物的动态响应，爆破技术的研究等。
4） 在医学、生物工程中：脑电波、心电波、脉搏波动等的信号处理等。
第12页/共35页
2途径：
1）从具体的工程对象提炼出力学模型 2）建立数学模型------应用力学知识建立所研究问题的数学模型 3）对数学模型进行分析和计算，求出请确、近似或数值解。 4） 比较------将计算结果与工程问题的实际现象或实验研究的测试结果进行 比较，考察理论结果是否解决该工程问题，如不能解决而数学模型及求解均无错 误，则需要修改力学模型重复上述过程。
第9页/共35页
5 随机振动
20世纪50年代，航空和航天工程的发展对振动力学提出了更高 的要求，确定性的力学模型无法处理包含随机因素的工程问题----如大气湍流引起的飞机颤振、喷气噪音导致飞行器表面结构 的声疲劳、火箭运载工具有效负荷的可靠性等。工程的需要迫使 人们用概率统计的方法研究承受非确定性载荷的机械系统和结构 的响应、稳定性和可靠性等， 从而 形成了随机振动这一振动力 学的重要组成部分。 在工程问题中振动信号的采集和处理是随机振动理论应用的前提， 由于计算机的迅速发展和快速第1傅0页/立共35叶页 变换算法的出现，随机振动

第四章振动下

第四章振动下

结论： 结论：
振子在振动过程中， （1） 振子在振动过程中，动能和势能分别随时间 变化，但任一时刻总机械能保持不变。 变化，但任一时刻总机械能保持不变。 （2） 动能和势能的变化频率是弹簧振子振动频 率的两倍。 频率一定时， （3）频率一定时，谐振动的总能量与振幅的平方 成正比。（适合于任何谐振系统） 。（适合于任何谐振系统 成正比。（适合于任何谐振系统） 弹性势能
小结：
描述简谐振动的三种方法： 描述简谐振动的三种方法： 运动方程，振动曲线，旋转矢量。 运动方程，振动曲线，旋转矢量。
的简谐振动， 例1：一物体沿 轴作振 幅为 A 的简谐振动，若初始时该球的 ：一物体沿x轴作振 状态为（ ） ；（2）在平衡位置且向X轴正方向运动 轴正方向运动； 状态为（1）X0＝ -A；（ ）在平衡位置且向 轴正方向运动； ；（ 处向X轴负方向运动；（4） 轴负方向运动；（ （3）在 X0＝1／2 A 处向 轴负方向运动；（ ）在 ） ／ 方向运动。试用旋转矢量法确定相应的初相位。 处向正 方向运动。试用旋转矢量法确定相应的初相位。 3π r ϕ = ϕ =π
k = m
得
X
g b
mg
b, v 0 = 0
g t+π) b
A =b, φ = π
[ 例2] 一谐振动的振动曲线如图所示。 一谐振动的振动曲线如图所示。
ω 以及振动方程。 求： ϕ 0 以及振动方程。
−
π
x
x
A 2
3r
A
1.0
0
解：
t
r A
A
π
2
x
π
3
t=
A x0 = = A cos ϕ 0 2 0时 v 0 = − ω A sin ϕ 0 > 0

简谐振动旋转矢量法讲课文档

简谐振动旋转矢量法讲课文档
机械振动, 电磁振荡 机械波, 电磁波 德布罗意波——几率波
振动学是波动学的基础
第5章 机械振动
振动: 任何一个物理量(物体的位置, 电 流强度, 电场强度, 磁场强度等)在某一 固定值附近作往复变化. 机械振动: 物体在固定位置(平衡位置) 附近作来回往复的运动. 简谐运动: 是最基本, 最简单的振动.
ω 6π 6
第18页，共20页。
§ 5.3 单摆
O
l T
mg
小球受力矩:
Mmg siln
根据转动定律
M J
mgslinm2ldd2t2
化简得:
d2
dt2
gsin
l
0
当θ 很小时, sin
d2
dt2
g l
0
结论: 单摆振动是简谐运动
0 cos t
g
l
T 2π l g
θ为振动角位移,θ0叫做角振幅
第19页，共20页。
例3: 一简谐振动曲线如图所示, 则振动周期
x（m 4） 2
1
t（s）
2 4 cos
0 4cos
3
32
5
6
T 2 12 5
（A）2.62 s （B）2.40 s （C）0.42 s （D）0.382 s
答案: B
第20页，共20页。
v d x 0.24sin 6.0t dt
sin 6.0t 1 cos2 6.0t
1
1
2
3
2 2
依题意, v＜0
v 0.24 3 0.208 m s1 2
第11页，共20页。
§5.2 简谐运动的旋转矢量 表示法
5.2.1 旋转矢量表示法

《简谐振动的描述》-PPT

《简谐振动的描述》-PPT

根据牛顿第二定律，有： kx m d 2 x dt 2
令 2 k 有：
m
d 2x dt 2
2x
简谐振动方程
解微分方程→
A, 为积分常数
0
注意：除弹簧振子外，单摆、复摆做
小角度（一般<=5°）摆动等都可以
视为简谐振动
§简谐振动的速度、加速度
x 简谐振动的位移： A cos(t )
v 简谐振动的速度： dx A sin( t )
▪
广义地讲：振动指任何一个物理量在某一定值附近作周期性的往复变化
▪
狭义地讲：振动指物体在其平衡位置附近的往复运动
▪
振动依机理不同区分为机械振动、电磁振动，但描述和研究方法相同。简谐振动是最简单、最基本的振动，任何复杂的振动都可以认为是由许多简谐振动的合成。因此研究简谐振动是进一步研究复杂振动的基础。接下来我们就一起来看一看简谐振动的描述。
t 0.83(s)
26
y
x
o
A
3
谢 谢！
2A
a
Ax
T
o tAvFra bibliotek如何通过振动曲线判断v正负、φ值？
5
5
§描述简谐振动三个特征量
▪ 圆频率（角频率）：在2π秒内物 体所作的完全振动的次数（rad·s1）
A
x
2 0
v0
2
▪
相位：相位是描述振动状态的物理量
▪
与状态参量 x,v 有一一对应关系
▪
每一时刻运动状态（x,v）是唯一的
0
arctg(
简谐振动除了用三角函数 式及振动曲线描述外还可 以用一个旋转矢量来表示 简谐运动，直观地表明简 谐运动的三个特征量的物 理意义。

简谐振动的旋转矢量图示.ppt

简谐振动的旋转矢量图示.ppt

角频率ω
A 与参考方向x 的夹角
振动相位ωt+φ0
3、两个谐振动的相位差
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
相位差为 (t 2 ) (t 1) 2 1
采用旋转矢量表示为：
A2
2
A1
1
O
x
例1、两个同频率的谐振动，它们都沿x轴振动，且振
幅相等，当t =0时质点1在x=A/2处向左运动,另一质点
F kx m 2x
(0.01kg)(π s1)2 (0.069m) 1.70103 N
2
（2）由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
解法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04m (0.08m) cos[(π s1)t π ]
x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
3 a 0.12 2 cos( 0.5 ) 1.03 m/s2
3
在t =T/4=0.5s时，可得
可得x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
sin0 0
0
3
简谐振动表达式 x 0.12cos( t ) m
3
因为
（2）由简谐振动的运动方程 x 0.12cos( t ) m
3
可得
v dx 0.12 sin( t ) m/s
dt
3
a dv 0.12 2 cos( t ) m/s2

物理-简谐振动的基本特征与旋转矢量图示法

物理-简谐振动的基本特征与旋转矢量图示法

研究简谐振动的重要性
机械振动的分类（从振动形式分） 连续振动、非连续振动； 周期振动、非周期振动…；
最简单、最基本的振动 —— 简谐运动.
简谐运动
合成 分解
复杂振动
机械振动第一讲
简谐振动的基本特征 旋转矢量图示法
一、简谐振动的定义
简谐振动
物体运动过程中，如果离开平衡位置的位 移（或角位移）按余弦函数（或正弦函数） 的规律随时间变化的运动，称为简谐振动。
三、简谐振动的三个特征量
4、振幅(A)与初相()的确定
设
注意 应根据
的符号确定 的象限范围。
三、简谐振动的三个特征量
讨论：两个同频谐振动的振动步调关系
谐振动1 x1 A1 cos(t 1 )
谐振动2 x2 A2 cos(t 2 )
相位差 (t 2 ) (t 1) 2 1
x
1）若 2 1 0
2
x轴负方向运动，而质点2在-A处。
试用旋转矢量法求这两个谐振动的初相差，及 两个质点第一次通过平衡位置的时刻。
四、简谐振动的旋转矢量图示法
小结：用旋转矢量法求相位或相位差的
O
x
第一步：由质点的位移x的值确定旋转矢量动端投影点 在x轴上的位置；
第二步：过该点作x轴的垂线，与矢量参考圆交于两点； 第三步：由质点振动速度的方向确定旋转矢量的位置。
运动学方程： 2、圆频率（ω）
最小正周期
完成一次全振动所需的时间
振动周期
振动频率 （系统固有）
三、简谐振动的三个特征量
运动学方程：
3、初相（ ）
振动速度 振动加速度
若A与确定：物体在t时刻的（x,v,a） 仅由( t + ) 决定。 称( t + ) 为物体在 t 时刻振动的相位(或)。 t =0 时的相位 ——初相位（或初相）

§3.2 简谐振动的旋转矢量图示【VIP专享】

§3.2 简谐振动的旋转矢量图示【VIP专享】
F kx m 2x
(0.01kg)(π s1)2 (0.069m) 1.70103 N
2
（2）由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
解法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04m (0.08m) cos[(π s1)t π ]
sin0 0
0
3
简谐振动表达式 x 0.12cos( t ) m
3
因为
（2）由简谐振动的运动方程 x 0.12cos( t ) m
3
可得
v dx 0.12 sin( t ) m/s
dt
3
a dv 0.12 2 cos( t ) m/s2
dt
3
在t =T/4=0.5s时，可得
x (0.08m) cos[(π s1)t π ] 3
2
3
v0 0
π
3
A
π3
x/m
0.08 0.04 o 0.04 0.08
x (0.08m) cos[(π s1)t π ]
2
3
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
t 1.0s 代入上式得 x 0.069m
2
3
v
x/m
0.08 0.04 o 0.04 0.08
cos( t ) 1
23 2
t 2 或 4
233 3
又因为第一次到达- 0.04m处时，v 0
即v A sin(t ) 0
23
所以t 2
23 3
t 2s 3

简谐振动 旋转矢量法

简谐振动 旋转矢量法
找到谐振动的特征量，问题就解决了。
振动方程为 x 2cos(5 t 2 )
3
16-4 简谐振动的合成
一、同方向、同频率谐振动的合成
某质点同时参与两个同频率且在同一条直线上的简谐运动
x1 A1 cos t 1 令 Asin A1 sin1 A2 sin2
x2 A2 cos t 2
2 (rad/s)
T
x Acos(t 0 ) t = 0 时： cos0 x0 / A 1/ 2,
0



3
初速度方向指向平衡位置，
v0 A sin 0 0,
0


3
A = 5 (m);
(rad/s)
x 5cos(t 3) (m)
例题5 ：
普通物理学教案
某振子x-t 图和v-t 图如下，写出振子的 运动学方程。
解： 由x - t 图，A = 2， x0 = -A / 2，向平衡位置移动
4
3 或 2
3
x-t 图上ω或T 信息不明确，再看v-t 图 vmax 10m/s 由速度幅 vmax A ， vmax / A 5s-1
P x
A
M
<
注意：旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意：旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意：旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意：旋转矢量在第 4 象限
速度v 0
P x
A

11-1简谐振动旋转矢量表示法

11-1简谐振动旋转矢量表示法

以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
第十一章 振 动
3
大学物 理学
1111-1 简谐振动的旋转矢量表示法
ω
t =t
ωt + ϕ
v A
x
o
x = A cos(ωt + ϕ )
以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
x1 = A1 cos(ωt + ϕ1 ) x2 = A2 cos(ωt + ϕ 2 )
∆ϕ = (ωt + ϕ 2 ) − (ωt + ϕ1 )
∆ϕ = ϕ 2 − ϕ1
第十一章 振 动
10
大学物 理学
1111-1 简谐振动的旋转矢量表示法
∆ϕ = ϕ 2 − ϕ1
∆ϕ = 0 同步
∆ϕ = ±π 反相 ∆ϕ为其它
简谐运动， （1）对同一简谐运动，相位差可以给出 ） 同一简谐运动 两运动状态间变化所需的时间． 两运动状态间变化所需的时间．
x1 = A cos(ωt1 + ϕ )
x2 = A cos(ωt 2 + ϕ )
∆ϕ = (ωt2 +ϕ) −(ωt1 +ϕ)
∆t = t2 −t1 = ∆ϕ
ω
第十一章 振 动
x = 0.104m v = −0.188m / s 2 a = −1.03m / s
A
− 0.12 −0.06
t 时刻
x/m
0.12
起始时刻
15
o
π − 3
0.06
A
第十一章 振 动
ω
大学物 理学

4.3 简谐振动的旋转矢量法

4.3 简谐振动的旋转矢量法

2
大学物理
第一版
4.3 简谐振动的旋转矢量法
t t
A
o

t
x
以o 为原点 旋转矢量 A 的 端点在 x轴上的 投影点的运动为 简谐运动.
x A cos(t )
3
大学物理
第一版
4.3 简谐振动的旋转矢量法
x A cos(t )
以o 为原点 的端 旋转矢量 A 点在 x 轴上的投 影点的运动为简 谐运动.
讨论

相位差：表示两个相位之差
（1）对同一简谐运动，相位差可以给出两运 动状态间变化所需的时间．
x1 Acos( )
t t 2 t1
x2 Acos( t2 )

9
大学物理
第一版
4.3 简谐振动的旋转矢量法
vm A
A
x A cos(t )
v a

v A sin(t )
x a A 2 n
a A 2 cos( t )
7
大学物理
第一版
4.3 简谐振动的旋转矢量法
3
用旋转矢量图画简谐运动的
xt 图
8
大学物理
第一版
4.3 简谐振动的旋转矢量法
0.08
17
大学物理
第一版
4.3 简谐振动的旋转矢量法
法二
t
时刻

t
π3 π3
起始时刻
x/m
0.08
0.08 0.04
o
0.04
π π 2 1 rad s t 0.667 s t 3 2 3
18
大学物理

矢量图示法

矢量图示法

x/cm
0 -1 -2
1
t/s
例3 作简谐运动的物体，由平衡位置向 x轴正方向运动，试问经过下列路程所需的 最短时间各为周期的几分之几？（1）由平 衡位置到最大位移处；（2）由平衡位置到 x=A/2处；（3）由x=A/2处到最大位移处.
一、矢量图示法
3、矢量图示法定义
象这种用旋转矢量在 坐标轴上的投影描述简谐 振动的方法就称为矢量图 示法
一、矢量图示法
4、谐振动的弹簧振子
一、矢量图示法
4、谐振动的弹簧振子
一、矢量图示法
4、谐振动的弹簧振子
一、矢量图示法
4、谐振动的弹簧振子
一、矢量图示法
4、谐振动的弹簧振子
一、矢量图示法
4、谐振动的弹簧振子
结论：
当谐振动物体向x轴负向运动时， 所对应的矢量 A位于一、二象限或y轴正 向； 当谐振动物体向 x 轴正向运动时，所 对应的矢量 A位于三、四象限或y轴负向； 当谐振动物体速度为零时，所对应 的矢量 A位于x轴上；
用矢量图示法做振动图象
物理学
第五版
例1 一个质点作简谐运动，振幅为A， A 在起始时刻质点的位移为 ,且向x轴 2 正方向运动，代表此简谐运动的旋转矢 量为（ ）
速度在x轴上的投影： Aωc o s(ωt+φ+π/2)=-Aωsin(ωt+φ)
一、矢量图示法
2、旋转矢量的速度、加速度
ωt+φ+π
a
ωt+φ
加速度在x轴上的投影：
Aω2cos(ωt+φ+π)=-Aω2cos(ωt+φ)
一、矢量图示法
3、矢量图示法定义
综上所述，如果使得： ①旋转矢量的长度等于谐振动的振幅A； ②矢量A逆时针旋转的角速度等于 谐振动的角频率ω； ③t=0时，A与x轴的夹角等于谐振动的 初相Φ。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

x 0.104m v 0.188m / s
a 1.03m / s2
A
t 时刻
x/m
0.12 0.06 o π0.06 0.12
3
A
起始时刻
第十一章 振 动
15
大学物 理学
11-1 简谐振动的旋转矢量表示法
（3）从初始时刻开始第一次通过平衡位 置的时刻.
通过平衡位置时，x=0，则由位移公式：
12
大学物 理学
11-1 简谐振动的旋转矢量表示法
又 v Asin(t ) 则 v0 Asin()
根据题意 v0 0
则
3
简谐运动表达式为：
x 0.12 cos( t )
3
0.12 0.06 o π0.06 0.12
v0
0,
3
3
A
x/m
第十一章 振 动
13
大学物 理学
11-1 简谐振动的旋转矢量表示法
相位的意义: 表征任意时刻（t）物体振动状态
（相貌）. 物体经一周期的振动，相位改变 2π .
第十一章 振 动
7
大学物 理学
11-1 简谐振动的旋转矢量表示法
讨论 ➢ 相位差：表示两个相位之差
（1）对同一简谐运动，相位差可以给出 两运动状态间变化所需的时间．
x1 Acos(t1 ) x2 Acos(t2 )
0 0.12 cos(t )
3
所以：t (2k 1) , k 1, 2,
3
2
k
t
6
第十一章 振 动
16
大学物 理学
11-1 简谐振动的旋转矢量表示法
第一次过平衡点时，k=1，所以：
5
t 6 5 0.83(s)
6
A
x/m
0.12 0.06 o π0.06 0.12
3
A
起始时刻
(t2 ) (t1 )
t
t2
t1
第十一章 振 动
8
大学物 理学
x
Aa
A2
b
o A v
11-1 简谐振动的旋转矢量表示法
t A
tb
x o A ta A
2
π
3
t π 3T 1 T 2π 6
第十一章 振 动
9
大学物 理学
11-1 简谐振动的旋转矢量表示法
（2）对于两个同频率的简谐运动，相位 差表示它们间步调上的差异（解决振动合成
A
t
x
x Acos(t )
点旋以转o矢为量原A
的端点在 x轴
上的投影点的
运动为简谐运
动.
第十一章 振 动
4
大学物 理学
11-1 简谐振动的旋转矢量表示法
y
vm t π
2
t an
A
O a v x
vm A
v A sin(t )
an A 2
x Acos(t )
a A2 cos(t )
大学物 理学
11-1 简谐振动的旋转矢量表示法
旋转矢量
自Ox轴的原点 O作一矢量 A，使 它 振的 幅模A ，等并于使振矢动量的A
在 Oxy平面内绕点
O作逆时针方向的
匀角速转动，其角
速度 与振动频率
相等，这个矢量就 叫做旋转矢量.
第十一章 振 动
1
大学物 理学
11-1 简谐振动的旋转矢量表示法
x Acos(t )
（2）t T / 4 时，质点的位置、速度、加速度
此简谐运动的速度为：
v Asin(t ) 0.12 sin( t )
3
加速度为：
a 2 A cos(t ) 0.12 2 cos( t )
3
第十一章 振 动
14
大学物 理学
11-1 简谐振动的旋转矢量表示法
将t=T/4=0.5s分别代入位移、速度、加 速度的公式，得：
点旋以转矢o为量原A
的端点在 x轴
上的投影点的
运动为简谐运
动.
第十一章 振 动
2
大学物 理学
11-1 简谐振动的旋转矢量表示法
t 0
o
A
x0 x
x0 Acos
点旋以转o矢为量原A
的端点在 x轴
上的投影点的
运动为简谐运
动.
第十一章 振 动
3
大学物 理学
11-1 简谐振动的旋转矢量表示法
t t
o
第十一章 振 动
5
大学物 理学
11-1 简谐振动的旋转矢量表示法
用旋转矢量图画简谐运动的x t图
第十一章 振 动
6
大学物 理学
11-1 简谐振动的旋转矢量表示法
相位 t
x A cos(t )
v A sin(t )
相位 (位相) (t) t
初相位 t 0时，(t)
问题）.
x1
A1
cos(t
1
)
x A cos(t )
2
2
2
(t 2 ) (t 1)
2
1
第十一章 振 动
10
大学物 理学
2 1
0同步 x
11-1 简谐振动的旋转矢量表示法
超前
π 反相 为其它 落后
x
x
o
to
o
t

t
第十一章 振 动
11
大学物 理学
11-1 简谐振动的旋转矢量表示法
例 一质点沿x轴作简谐运动，振幅 A=0.12 m，周期T=2 s，当t=0时，质点对平衡 位置的位移x0=0.06m.此时刻质点向x正向运动。 试求：
（1）此简谐运动的表达式
解 A 0.12 m 2 π s1
T
t 0，x0 0.06 m
代入 x Acos(t )
π
3
第十一章 振 动
第十一章 振 动
17