A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M P
A
x
注意:旋转矢量在第 2 象限 速度v < 0
M
P
A
x
注意:旋转矢量在第 3 象限 速度v 0
P M
A
<
x
注意:旋转矢量在第 3 象限 速度v 0
P x M
A
<
注意:旋转矢量在第 3 象限 速度v 0
2 1 2 2
若两分振动同相位:
2 1 2k
A A1 A2
k 0,1, 2,
两分振动相互加强
若两分振动反相位:
2 1 (2k 1)
A A1 A2
k 0,1, 2,
两分振动相互减弱
再若 A1= A2 , 则 A= 0
其它情况
A1 A2 A A1 A2
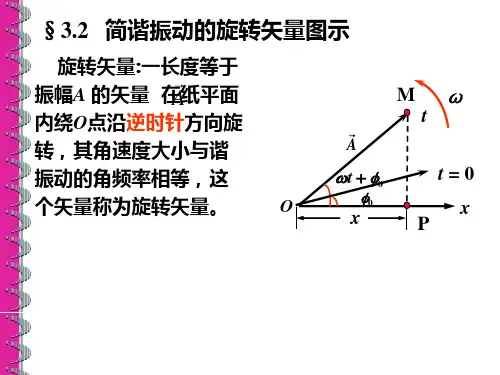
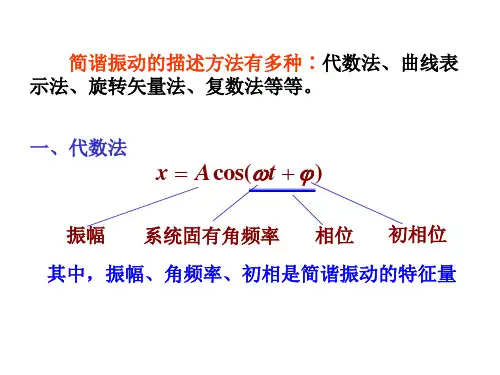
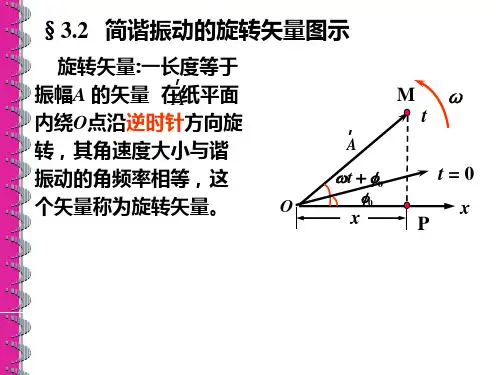
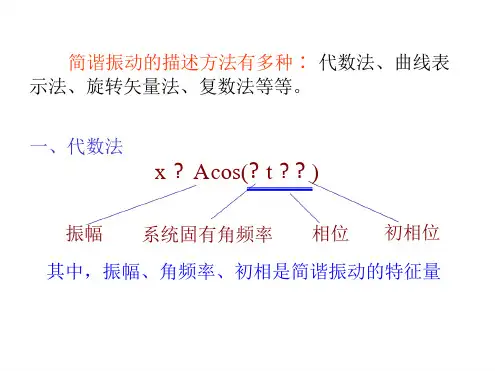
简谐振动的描述方法有多种∶代数法、曲线表 示法、旋转矢量法、复数法等等。
一、代数法
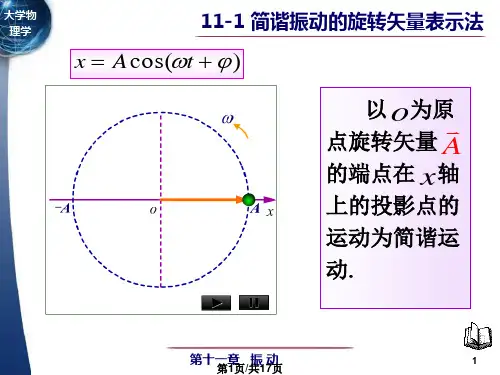
x A cos( t )
系统固有角频率 相位 初相位
振幅
其中,振幅、角频率、初相是简谐振动的特征量
二、图示法: (振动曲线) x A cos(t 0 )
三、复数法
z Ae
i ( t )
对应关系
t
用旋转矢量图画简谐运动的
x t
图
T 2π (旋转矢量旋转一周所需的时间)
A
P
M
x
注意:旋转矢量在第 1 象限 速度v < 0
A
P