电路原理：叠加定理

实验一叠加定理1.1.1实验目的1．用实验方法验证叠加定理，加深对该定理的理解。

2．加深对电路的电流、电压参考方向的理解。

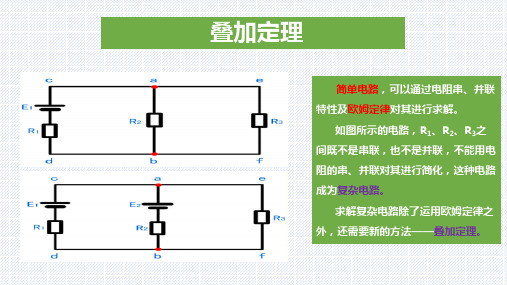
1.1.2 实验原理叠加定理指出：在有几个独立电源共同作用下的线性电路中，通过每一个元件的电流或其两端的电压，可以看成是由每一个独立电源单独作用时在该元件上所产生的电流或电压的代数和。

在实验中当一个电源单独作用时，其他的电源必须置为零（电压源短路，电流源开路）；在求电流或电压的代数和时，当电源单独作用时电流或电压的参考方向与共同作用时的参考方向一致时，符号取正，否则取负。

叠加定理反映了线性电路的叠加性，另外线性电路还具有齐次性，即当激励信号（如电源作用）增加或减小K倍时，电路的响应（即在电路其他各元件上所产生的电流和电压值）也将增加或减小K倍。

叠加性和齐次性都只适用于求解线性电路中的电流、电压。

对于非线性电路，叠加性和齐次性都不适用。

在本实验中，用直流稳压电源来近似模拟电压源，由其产生的误差可忽略不计，这是因为直流稳压电源的等效内阻很小。

1.1.3实验预习要求1．复习教材中叠加定理与计算方法，预习3.1.3中直流电压表、电流表、万用表和稳压电源的主要技术特性并掌握正确的使用方法。

2．按表1.1.1的要求，用支路电流法计算出图1.1.1电路中支路电流和各电阻元件两端的电压，注意参考方向，并把计算结果填入表1.1.1中。

3．利用EDA软件对图1.1.1电路进行仿真分析。

软件详细介绍见教材和附录1。

电流表插座图1.1.1叠加定理的实验电路1.1.4实验设备与器件1．双路可调直流稳压电源2．数字万用表3．电阻器若干4．叠加定理实验电路板1.1.5 实验内容与步骤1．实验电路如图1.1.1所示，按实验电路图连接线路并调节电源参数值。

2．在电路图中接入电压表或电流表，当E1、E2共同作用时测量各支路电流及各电阻元件两端的电压，数据记入表1.1.1中。

3．当E1单独作用时，BC两点不接电源，直接用短路线相连。

电路实验报告叠加定理
实验名称：叠加定理的验证
一、实验目的：使用NIMultisium验证叠加定理。

二、实验原理：
在有多个独立源共同作用下的线性电路中，任一电压或电流都是电路中各个独立电源单独作用时，在该处产生的电压或电流的叠加。

通过每一个元件的电流或其两端的电压，可以看成是由每一个独立源单独作用时在该元件上所产生的电流或电压的代数和。

三、实验方案：
用Multisium画出如下电路图，并开始模拟运行，可以在电压表和电流表中观测到如图数值。

叠加定理的验证：图
1
叠加定理的验证：图2
叠加定理的验证：图3
四、实验结论：
通过上面3幅图我们不难观测出：
对于图1中R1上的电流，其显示值为1.5000，很明显为图2，图3中对应的电流表数值之和。

同理，可以得到图1中R3处的电流和R2上的电压也满足这种关系。

所以我们不难得出叠加定理。

叠加定理适用范围一、引言叠加定理（Superposition Theorem）是电路分析中常用的一种方法，通过将电路分解为不同的独立电源进行分析，然后再将结果进行叠加得到最终的解。

这一定理在解决复杂电路问题时具有很大的优势，然而，叠加定理并非适用于所有电路。

本文将探讨叠加定理的适用范围，并提供一些例子来说明其中的限制和局限性。

二、叠加定理的基本原理叠加定理的基本原理可以概括为：在一个线性电路中，如果有多个独立电源作用于电路中，那么最终的电流或电压等可由各个单独电源所产生的效应叠加而成。

如果一个电路中有多个电源，我们可以把每个电源的作用看成是单独进行分析，最后将它们的效应相加得到整个电路的解。

三、叠加定理的适用范围尽管叠加定理对于解决复杂电路问题非常有用，但它并非适用于所有电路。

以下是叠加定理适用范围的一些主要方面：1.仅适用于线性电路：叠加定理只适用于线性电路，即电流与电压之间满足线性关系的电路。

对于非线性电路，叠加定理并不适用，因为非线性元件的电流-电压关系不满足叠加原理。

2.叠加定理不适用于功率和能量：叠加定理可以用于计算电路中特定节点的电压或电流，但它并不能直接计算功率和能量。

功率和能量通常需要通过其他方法进行分析和计算。

3.独立电源：叠加定理只适用于有多个独立电源的电路。

如果电路中的电源相互依赖或由其他因素控制，叠加定理将无法正确应用。

4.线性叠加：叠加定理适用于线性叠加的电路。

线性叠加是指电路响应与输入的线性组合成正比例。

如果电路的响应不满足线性叠加条件，叠加定理将无法得到正确的解。

五、例子和案例分析为了更好地理解叠加定理的适用范围，我们来看几个例子：1.并联电阻：假设有一个由两个电阻 R1 和 R2 并联组成的电路，并且电路中有一个电压源 V。

我们可以使用叠加定理来计算每个电阻上的电流。

关闭电压源 V，只保留 R1，并计算电流 I1。

关闭 R1，只保留 R2，并计算电流 I2。

将这两个电流相加得到总电流 I = I1 + I2。