第7章 扭转变形

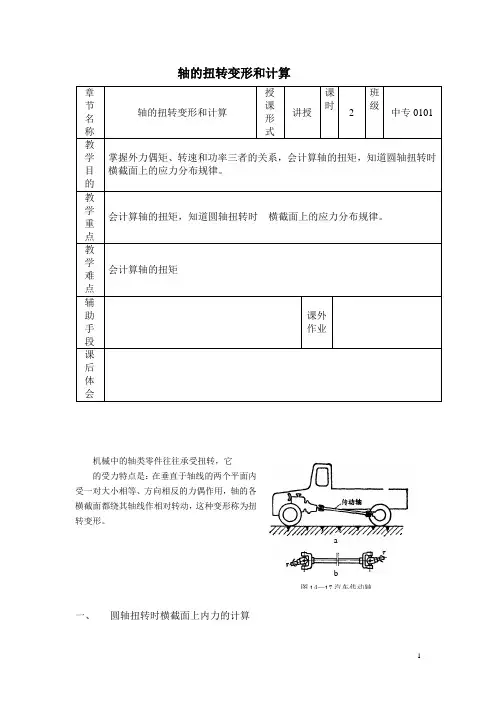
ab图14—17汽车传动轴轴的扭转变形和计算章节名称 轴的扭转变形和计算授课形式讲授课时2班级中专0101教学目的 掌握外力偶矩、转速和功率三者的关系，会计算轴的扭矩，知道圆轴扭转时 横截面上的应力分布规律。

教学重点 会计算轴的扭矩，知道圆轴扭转时 横截面上的应力分布规律。

教学难点 会计算轴的扭矩辅助手段课外作业课后体会机械中的轴类零件往往承受扭转，它 的受力特点是：在垂直于轴线的两个平面内受一对大小相等、方向相反的力偶作用，轴的各横截面都绕其轴线作相对转动，这种变形称为扭转变形。

一、圆轴扭转时横截面上内力的计算图14—18截面法求扭矩l 、外力偶矩：为了求出圆轴扭转时截面上的内力，必须先计算出轴上的外力偶矩，作用在轴上的外力偶矩往往不是直接给出的，而是根据给定的轴的传递功率和轴的转速算出来的，功率、转速和外力偶矩三者间的关系是：M ＝9550 P ／n式中：P ——轴传递的功率(千瓦， KW) n ——轴的转速(转／分， r ／ min) M ——作用在轴上的外力偶矩(牛顿米，Nm)2、扭转时横截面上的内力——扭矩圆轴在外力偶矩的作用下，横截面上产生内力。

求内力的方法仍用截面法。

右图表示装有四个皮带轮的传动轴，在四个带轮上分别作用有主动力偶矩 M 1和从动力偶矩M 2、M 3、M 4，外力偶矩分别为 M 1＝110Nm ，M 2=60Nm ，M 3=20Nm ， M 4=30Nm 。

若计算 AB 段内任一截面上的内力，可假想沿该段内的任一截面1—1将轴截开，取左边部分为研究对象。

如图所示。

为了保证该段的平衡，必须以内力偶矩 Mn 1代替另一部分对被研究部分的作用， Mn 1称为扭矩。

扭矩的正负有如下规定：使右手拇指与截面法线的方向一致，若截面上的扭矩的转向与其它四指的转向相同，则扭矩取正号：反之取负号。

应用截面法时，一般都先假设截面上的扭矩为正。

扭矩的大小用平衡方程Σm=0求得，即AB 段内： Σm=0， M 1十Mn 1＝0Mn 1＝一M 1＝一l10 Nm (设反)图14—19圆轴扭转变形图14—20圆轴的横截 面上剪应力的分布规律BC 段内： Σm ＝0 M 1—M 2＋Mn 2＝0 得 Mn 2＝—50 Nm (设反) CD 段内： Σm ＝0 M 1—M 2—M 3十Mn 3＝0 得 Mn 3＝—30 Nm (设反) 为了清楚地看出各截面上的扭矩变化情况，以便确定危险截面，通常把扭矩随截面位置的变化绘成图形，称为扭矩图。

第7章 扭转7．1 扭转的概念和工程实际中的扭转问题扭转变形是杆件的基本变形之一。

它的外力特点是杆件受力偶作用，力偶作用在与轴线垂直的平面内，如图7-1所示。

杆件的变形特点是：杆件的任意两个横截面围绕其轴线作相对转动，杆件的这种变形形式称为扭转。

扭转时杆件两个横截面绕轴线相对转动的角度称为扭转角（angle of twist ）ϕ。

以扭转变形为主的杆件通常称为轴。

工程上有很多圆截面等直杆，受到一对大小相等、方向相反的外力偶矩作用。

如图7-2所示的驾驶盘轴，在轮盘边缘作用一对方向相反的切向力构成一力偶。

根据平衡条件，在轴的另一端，必存在一反作用力偶，在此力偶矩作用下，各横截面绕轴线作相对旋转。

此轴产生的变形即为扭转变形。

在工程中，受扭杆件是很常见的，比如机械中的传动轴（图7-3）、攻螺纹所用丝锥的锥杆（图7-4）以及钻杆等，它们的主要变形都是扭转，但同时还可能伴随有拉压、弯曲等变形。

如果后者不大，往往可以忽略，或者在初步设计中，暂不考虑这些因素，将其视为扭转构件。

圆轴是最常见的扭转变形构件，本章主要讨论圆轴的扭转。

BAMAB ϕ图7-1图7-2图7-3图7-47. 2 杆件扭转时的内力要研究受扭杆件的应力和变形，首先需要计算杆件横截面上的内力。

一、外力偶矩的计算作用于圆轴上的外力偶矩往往不是直接给出的，通常是给出轴的转速n 和轴所传递的功率P 。

此时需要根据功率、转速、力矩三者之间的关系来计算外力偶矩的大小。

以工程中常用的传动轴为例，已知它所传递的功率P 和转速n ，作用在轴上的外力偶矩可以通过功率P 和转速n 换算得到。

因为功率是每秒钟内所做的功，有602101033πωn M M P e e ⨯⨯=⨯⨯=−− 于是，作用在轴上的外力偶矩为nPM e 9550= (7-1) 式中:M e —作用在轴上的外力偶矩，单位为N·mP —轴传递的功率， 单位为kW ω—转轴的角速度，单位为rad/s n —轴的转速，单位为是r/min 。

第四章 扭转4.1预备知识一、基本概念 1、扭转变形扭转变形是杆件的基本变形之一，扭转变形的受力特点是：杆件受力偶系的作用，这些力偶的作用面都垂直于杆轴。

此时，截面B 相对于截面A 转了一个角度ϕ，称为扭转角。

同时，杆件表面的纵向直线也转了一个角度γ变为螺旋线，γ称为剪切角。

2、外力偶杆件所受外力偶的大小一般不是直接给出时，应经过适当的换算。

若己知轴传递的功率P(kW)和转速n(r/min)，则轴所受的外力偶矩)(9549Nm nPT =。

3、扭矩和扭矩图圆轴扭转时，截面上的内力矩称为扭矩，用T 表示。

扭矩的正负号，按右手螺旋法则判定。

如扭矩矢量与截面外向法线一致，为正扭矩，反之为负；求扭矩时仍采用截面法。

扭矩图是扭矩沿轴线变化图形，与轴力图的画法是相似4、纯剪切 切应力互等定理单元体的左右两个侧面上只有切应力而无正应力，此种单元体发生的变形称为纯剪切。

在相互垂直的两个平面上，切应力必然成对存在且数值相等，两者都垂直于两个平面的交线、方向到共同指向或共同背离积这一交线，这就是切应力互等定理。

5、切应变 剪切虎克定律 对于纯剪切的单元体，其变形是相对两侧面发生的微小错动，以γ来度量错动变形程度，即称切应变。

当切应力不超过材料的剪切比例极限时，切应力τ和切应变γ成正比，即τ=G γG 称材料的剪切弹性模量，常用单位是GPa 。

6、圆杆扭转时的应力和强度计算(1) 圆杆扭转时，横截面上的切应力垂直于半径，并沿半径线性分布，距圆心为ρ处的切应力为ρτρpI T =图式中T 为横截面的扭矩，I p 为截面的极惯性矩。

(2) 圆形截面极惯性矩和抗扭截面系数实心圆截面324D I p π=， 163D W p π=（D 为直径） 空心圆截面)1(3244a D I p -=π， )1(1643απ-=D W p （D 为外径，d 为内径，D d /=α）(3)圆杆扭转时横截面上的最大切应力发生在外表面处tW T =max τ 式中W t =I p /R ，称为圆杆抗扭截面系数（或抗抟截面模量）。