扭转应力及变形
- 格式:pdf
- 大小:437.50 KB
- 文档页数:32


04、基本知识 怎样推导轴向拉压和扭转的应力公式、变形公式(供参考)同学们学习下面内容后,一定要向老师回信(****************),说出你对本资料的看法(收获、不懂的地方、资料有错的地方),以便考核你的平时成绩和改进我的工作。
回信请注明班级和学号的后面三位数。
1 * 问题的提出 ........................................................................................................................... 1 2 下面就用统一的步骤,研究轴向拉压和扭转的应力公式和变形公式。
........................... 2 3 1.1 轴向拉压杆的应力公式推导 ............................................................................................ 2 4 1.2 轴向拉压杆的变形公式推导 ............................................................................................ 4 5 1.3 轴向拉压杆应力公式和变形公式的简要推导 ................................................................ 4 6 1.4 轴向拉压杆的强度条件、刚度条件的建立 .................................................................... 4 7 2.1 扭转轴的应力公式推导 .................................................................................................... 5 8 2.2 扭转轴的变形公式推导 .................................................................................................... 7 9 2.3 扭转轴应力公式和变形公式的简要推导 ........................................................................ 7 10 2.4 扭转的强度条件、刚度条件的建立 ............................................................................ 8 11 3. 轴向拉压、扭转、梁的弯曲剪切,应力公式和变形公式推导汇总表 .. (9)1* 问题的提出在材料力学里,分析杆件的强度和刚度是十分重要的,它们是材料力学的核心内容。

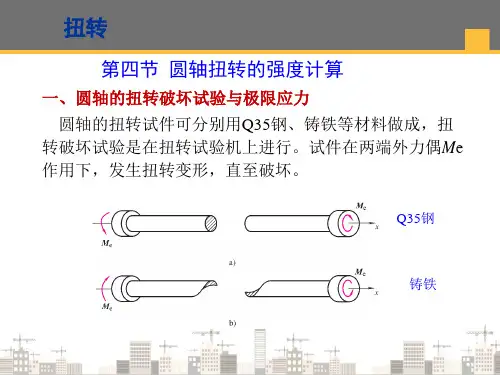


扭转切应力两类切应力扭转切应力弯曲切应力扭转切应力圆轴扭转时的应力变形特征圆轴扭转时横截面上的切应力分析矩形截面杆扭转切应力公式圆轴扭转时的应力变形特征外加力偶矩与功率和转速的关系变形特征横截面和纵截面都有切应力存在--切应力互等定理外加力偶矩与功率和转速的关系应用此公式时要注意单位。
将圆轴表面如图划分为许多小方块,这些小方块可近似地看作矩形。
轴受扭以后,小方块就发生变形,变成菱形。
如图是放大后的情形。
产生这样的变形是因为在两个横截面上出现了切应力。
作用在AB、CD面上的切应力组成一个力偶,显然它是不能使这个微元平衡的,因此,在两个纵截面上也产生切应力。
通过应变知道横截面上有切应力,再通过平衡知道纵截面上也有切应力。
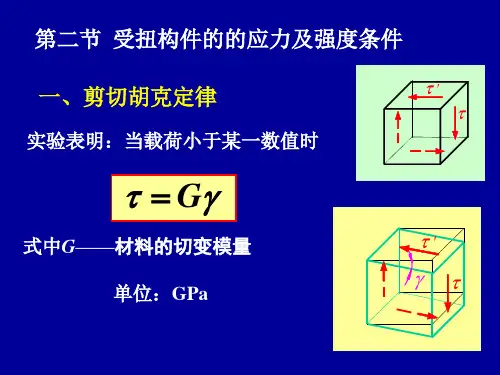
微元的直角改?横截面上和纵截面上的切应力有何关系?我们取出如图微元分析,横截面上的切应力τ乘以其作用面积dydz,再乘以力臂dx,组成一个力偶;纵截面上的切应力τ'也同样组成一个力偶,这两个力偶是大小相等,方向相反的。
最后消掉公因子dxdydz,就得到τ=τ'。
根据平衡的要求?圆轴扭转时横截面上的切应力根据变形特征和切应力互等定理,现在分析圆轴扭转时横截面上的切应力。
反对称分析论证平面保持平面由平面保持平面导出变形协调方程由物性关系得到应力分布切应力公式方法与过程反对称分析论证平面保持平面首先用反对称关系。
如图,对称圆轴两端作用一对反对称的力偶,横截面上C、D两点若不保持在原来的平面上,则从A端看,力偶是顺时针方向的,这两点背离观察者而去的;若从B端看,力偶也是顺时针方向的,C、D两点也背离观察者而去。
显然这是矛盾的,因此,C、D两点只能?第一个结论圆轴扭转时,横截面保持平面,平面上各点只能在平面内转动还可以用反对称关系作进一步分析这些平面上的点移动的规律。
观察截面上的一条直径,若发生扭曲,当分别从A、B两端看过去时,一次呈S形,一次呈反S形,同样产生矛盾的结论。
最终结论圆轴扭转时,横截面保持平面,并且只能发生刚性转动。

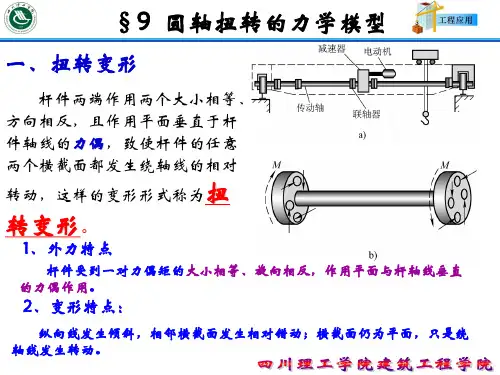

扭转杆件的应力计算公式在工程学中,扭转杆件是一种常见的结构元件,它们通常用于承受扭转力或者转矩。
在设计和分析扭转杆件时,计算其应力是非常重要的。
本文将介绍扭转杆件的应力计算公式以及相关的理论知识。
扭转杆件的应力计算公式可以通过以下步骤推导得到。
首先,我们需要了解扭转杆件的基本几何形状和材料性质。
扭转杆件通常是圆柱形状的,其直径为d,长度为L。
材料的弹性模量为E,剪切模量为G。
在扭转杆件上施加一个扭矩T,我们可以得到以下的应力计算公式:τ = Tr/J。
其中,τ是扭转杆件上的剪切应力,T是施加在扭转杆件上的扭矩,r是扭转杆件上某一点到中心轴的距离,J是扭转杆件的极惯性矩。
极惯性矩J可以通过以下公式计算得到:J = πd^4/32。
通过将极惯性矩J代入到剪切应力的公式中,我们可以得到扭转杆件上的最大剪切应力:τ_max = Tc/J。
其中,c是扭转杆件的半径。
最大剪切应力发生在扭转杆件的表面,其值可以用来判断扭转杆件的强度和稳定性。
在实际工程中,我们通常需要计算扭转杆件上的最大剪切应力。
为了更好地理解扭转杆件的应力分布情况,我们可以绘制出扭转杆件上的剪切应力分布图。
根据应力计算公式,我们可以得到扭转杆件上不同点的剪切应力值,然后将这些值绘制成图表,以便工程师们更好地分析和理解扭转杆件的应力分布情况。
除了计算扭转杆件上的最大剪切应力外,我们还需要考虑扭转杆件的变形情况。
在扭转杆件上施加扭矩时,会产生一定的变形,这种变形可以通过以下公式计算得到:θ = TL/(GJ)。
其中,θ是扭转杆件上某一点的角度变化,L是扭转杆件的长度,G是材料的剪切模量。
通过计算扭转杆件上不同点的角度变化,我们可以得到扭转杆件的整体变形情况。
在实际工程中,我们还需要考虑扭转杆件的疲劳寿命。
由于扭转杆件通常需要长时间承受扭转力,因此其疲劳寿命是非常重要的。
我们可以通过应力分析和疲劳试验来评估扭转杆件的疲劳寿命,以确保其在使用过程中不会发生断裂或者变形。

材料力学扭转应力材料力学中的扭转应力,指的是在材料中由于扭转作用而产生的应力。
扭转应力是材料力学中的基本概念之一,广泛应用于各种工程和结构设计中。
在材料力学中,扭转应力可由以下公式表示:τ=T*r/J其中,τ表示扭转应力,T表示应用在材料上的扭矩大小,r表示材料中的极径,J表示截面转动惯量。
从上述公式中可以看出,扭转应力与扭矩、极径以及截面转动惯量有关。
扭转作用会使材料发生变形,而扭转应力则是描述这种变形现象的力学量。
在实际工程中,我们常常需要计算材料在扭转作用下的变形和应力值,以保证结构的安全和可靠性。
扭转应力的计算和分析在工程设计过程中非常重要。
在旋转机械、传动轴、扭转梁、桥梁、挠性杆件等结构中,承受扭转作用的构件都需要进行扭转应力的计算。
只有通过准确地计算和分析扭转应力,才能保证这些结构的正常运行和使用。
在实际工程中,我们常常使用各种方法和理论来计算和分析扭转应力。
最常用的一种方法是应用弹性力学理论,即将材料视为弹性体,在假设材料的应变具有线性关系的基础上,引入材料的弹性模量和剪切模量等材料参数,进行扭转应力的计算。
另外,材料的形状和几何特征也对扭转应力产生影响。
对于圆形截面的材料,扭转应力分布为圆对称分布,与极径成反比。
而对于其他形状的截面,扭转应力的分布则会有所差异。
因此,在具体的工程设计中,需要分析材料的截面形状以及其他几何特征,以计算准确的扭转应力。
此外,材料的性质也会影响扭转应力的大小和分布。
不同材料的弹性模量和剪切模量不同,因此在应用扭转应力公式时,需要考虑到材料的特性。
总之,扭转应力是材料力学中的重要概念,对于工程设计和结构分析具有重要意义。
能够准确计算和分析扭转应力,可以保证工程结构的安全和可靠性。
因此,在实际工程中,我们需要充分理解材料的扭转应力,并结合具体的情况进行准确的计算和分析。
扭转的变形特点
扭转是一种物体在应力作用下发生的变形。
它具有以下特点:
1. 扭转变形是围绕物体的轴线进行的旋转变形,相对于其他形式的变形(如拉伸、压缩等),扭转变形是围绕一个中心轴线进行的。
2. 扭转变形产生的应力和应变分布不均匀,最大的应力出现在物体的表面附近,随着距离表面的增加而逐渐减小。
3. 扭转变形会引起物体的截面形状发生改变,原本圆形的截面可能会变成椭圆形或者其他形状。
4. 扭转变形会导致物体长度的变化,但总长度保持不变。
例如,在扭转过程中,物体的一部分可能会延长,而另一部分则会缩短。
5. 扭转变形通常发生在柔性材料上,如金属、塑料等。
刚性材料由于其高强度和低可变形性质,往往不容易发生明显的扭转变形。
这些特点使得扭转变形在许多工程领域中具有重要的应用,如机械设计、结构工程等。
1。
材料力学扭转应力
材料力学中,扭转应力是指作用于材料内部的扭转力产生的应力。
当材料受到扭转力作用时,其内部会产生一个对扭转力的阻抗,即扭转应力。
扭转应力主要在圆柱体或轴的表面上产生,其大小与扭转力的大小成正比,与材料的性质和几何形状有关。
扭转应力可以通过许多方式进行计算和描述。
其中最常用的描述方式是采用剪应力。
扭转应力可以通过剪应力(也称为切应力)的定义进行计算,即扭转力与扭转体的横截面面积的比值。
扭转应力可以在不同的横截面上具有不同的分布。
扭转应力的大小可以通过扭转弹簧常数(也称为剪切模量)衡量。
扭转弹簧常数是一个材料属性,描述了材料在扭转载荷下的应变与扭转应力之间的关系。
扭转弹簧常数越大,扭转应力产生的抵抗就越强。
扭转应力在很多工程应用中都是一个重要参数。
例如,在轴传动系统中,扭转应力是评估轴的耐久性和疲劳寿命的关键指标。
在材料加工中,扭转应力是评估材料变形和断裂的重要因素。
了解和控制材料的扭转应力可以帮助工程师设计更可靠和耐用的结构和零件。