第4章扭转变形
- 格式:pps
- 大小:1.90 MB
- 文档页数:50










第四章 扭转§4—1 工程实例、概念一、工程实例1、螺丝刀杆工作时受扭。
2、汽车方向盘的转动轴工作时受扭。
3、机器中的传动轴工作时受扭。
4、钻井中的钻杆工作时受扭。
二、扭转的概念受力特点:杆两端作用着大小相等方向相反的力偶,且作用面垂直杆的轴线。
变形特点:杆任意两截面绕轴线发生相对转动。
轴:主要发生扭转变形的杆。
§4—2 外力偶矩、扭矩一、外力:m (外力偶矩)1、已知:功率 P 千瓦(KW ),转速 n 转/分(r /min ; rpm)。
外力偶矩:m)(N 9549⋅=nPm 2、已知:功率 P 马力(Ps),转速 n 转/分(r /min ;rpm)。
外力偶矩:m)(N 7024⋅=nPm 二、内力:T (扭矩) 1、内力的大小:(截面法)mT m T mx==-=∑002、内力的符号规定:以变形为依据,按右手螺旋法则判断。
(右手的四指代表扭矩的旋转方向,大拇指代表其矢量方向,若其矢量方向背离所在截面则扭矩规定为正值,反之为负值。
)3、注意的问题:(1)、截开面上设正值的扭矩方向;(2)、在采用截面法之前不能将外力简化或平移。
4、内力图(扭矩图):表示构件各横截面扭矩沿轴线变化的图形。
作法:同轴力图:§4—3 薄壁圆筒的扭转 一、薄壁圆筒横截面上的应力(壁厚0101r t ≤,0r :为平均半径) 实验→变形规律→应力的分布规律→应力的计算公式。
1、实验:2、变形规律:圆周线——形状、大小、间距不变,各圆周线只是绕轴线转动了一个不同的角度。
纵向线——倾斜了同一个角度,小方格变成了平行四边形。
3、切应变(角应变、剪应变):直角角度的改变量。
4、定性分析横截面上的应力(1) 00=∴=σε ;(2)00≠∴≠τγ因为同一圆周上切应变相同,所以同一圆周上切应力大小相等。
⑶ 因为壁厚远小于直径,所以可以认为切应力沿壁厚均匀分布,而且方向垂直于其半径方向。
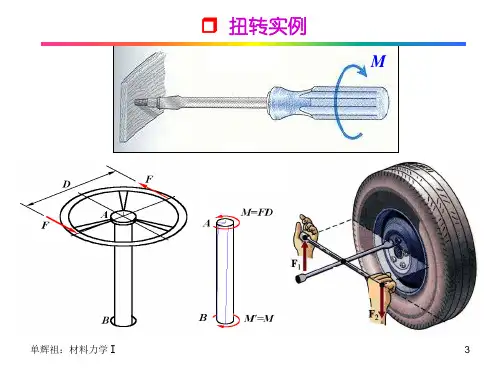
华北电力大学力学教研室第四章扭转§4-1 扭转的概念一、扭转实例:圆杆各横截面绕杆的轴线作相对转动受力特点:圆截面直杆受到一对大小相等、转向相反、作用面垂直于杆的轴线的外力偶作用(矢量与轴线一致)变形特点:M eM e工程中注意承受扭转的构件称为“轴”,实际构件工作时除发生扭转变形外,还常伴随有弯曲、拉压等其他变形形式。
§4-2 传动轴的外力偶矩· 扭矩及扭矩图Ⅰ、传动轴的外力偶矩传动轴的转速n ;所传递的功率P (kW)作用在该轮上的外力偶矩M e 。
已知:求:传动轮的转速n 、功率P 及其上的外力偶矩M e 之间的关系:)(024m N ⋅=nP7M e (P —马力))(550m N ⋅=n P9M e (P —kW)M eM eABⅡ、扭矩及扭矩图圆轴受扭时其横截面上的内力偶矩称为扭矩,用符号T 表示。
eM T 扭矩大小可利用截面法来确定。
11TTM e M eAB11BM e AM e11x扭矩的符号规定按右手螺旋法则确定:扭矩矢量离开截面为正,指向截面为负。
仿照轴力图的做法,可作扭矩图,表明沿杆轴线各横截面上扭矩的变化情况。
TTT (+)TTT (-)eM T 11TTM eM eAB11BM e AM e11xM eT 图+例一传动轴如图,转速n = 300r/min ;主动轮输入的功率P 1= 500kW ,三个从动轮输出的功率分别为:P 2= 150kW ,P 3= 150kW ,P 4= 200kW 。
试作轴的扭矩图。
首先必须计算作用在各轮上的外力偶矩mkN 9.15m N )3005001055.9(31⋅=⋅⨯⨯=M m kN 78.4m N )1001501055.9(332⋅=⋅⨯⨯==M M mkN 37.6m N )3002001055.9(34⋅=⋅⨯⨯=M 解:221133M 1M 2M 3M 4A BCD分别计算各段的扭矩mkN 78.421⋅-=-=M T m9.56kN 322⋅=+=M M T mkN 37.643⋅==M T 221133M 1M 2M 3M 4A B CDT 111xM 2AT 2AM 2BM 322xT 333DM 4x扭矩图T max = 9.56 kN·m 在CA 段内M 1M 2M 3M 4ABCD 4.789.566.37T 图(kN·m)表面变形特点及分析:§4-3 圆轴扭转时的应力·强度条件g jA B D C1、相邻圆周线绕杆的轴线相对转动,但圆周的大小、形状、间距都未变;2、纵向线倾斜了同一个角度g ,表面上所有矩形均变成平行四边形。
平面假设:圆轴受扭转时其横截面如同刚性平面一样绕杆的轴线转动。
表面正方格子倾斜的角度—直角的改变量g 切应变ggjA BD Cg ABC DB 1A 1D 1C 1D'D 1'C 1'C'横截面上没有正应力产生,只有切应力,方向与圆周相切,即与半径垂直。
此处为以横截面、径截面以及与表面平行的面从受扭的等直圆杆表面处截取一微小的正六面体单元体·切应力互等定理单元体——M eMexyzabO cdd xd yt 'ttt 'tt ='纯剪切应力状态:单元体在其两对互相垂直的平面上只有切应力而无正应力的状态称为纯剪切应力状态。
EG G G '=≈ρρg g tan AD DD '=≈g g tan xd d jρ=M eM ed j gD'G'G E TT O 1O 2a b abd xD Ag ρd jgD'G'GEO 1O 2D Ag ρd xdⅠ、横截面上的应力公式物理方面静力学方面几何关系A 、几何关系xR d d j ⨯=x d d j ρg ρ=xd d j 相对扭转角沿杆长的变化率,对于给定的横截面为常量ρg ρ∝d j gD'G'GE TT O 1O 2a b abd xD Ag ρd jgD'G'G E O 1O 2DAg ρd xd剪切胡克定律:(在弹性范围内,切应力与切应变成正比。
g t G =x G d d j ρt ρ=B 、物理方面ρt ρ∝xd d j ρg ρ=Od?横截面上各点的剪应力与点到截面中心的间距成正比,即剪应力沿截面的半径呈线性分布。
C 、静力学方面A d ρt ρT=⎰A T A x G A=⎰d d d 2ρj ⎰=AAI d 2p ρpd d GI Tx =j 称为横截面的极惯性矩t ρd AO令得T xG d d jρt ρ=圆轴扭转时横截面上切应力计算公式:p p IT GI T G ρρt ρ=⎪⎪⎭⎫ ⎝⎛=xG d d jρt ρ=pd d GI Tx =j pI T ρt ρ=Od t maxρt maxt ρT 1、T 为横截面上的扭矩2、Ip 为截面参数,取决于截面形状与尺寸3、ρ为所求点距圆心距离。
发生在横截面周边上各点处。
r=ρp maxI Tr =t 称为扭转截面系数rI W p p =最大切应力r I T /p =pW T =令即pm axW T =t t maxt maxOdρt ρT同样适用于空心圆截面杆受扭的情形pI T ρt ρ=pm ax W T =t t maxt max O D d T ρt ρ圆截面的极惯性矩I p 和扭转截面系数W p ⎰=A A I d 2p ρ16π2/3p p d d I W ==32π4d =实心圆截面:—几何性质O d D O d()431162/α-==D D I W πp p ()44132πα-=D ⎰=A A I d 2p ρⅢ、强度条件][max t t ≤等直圆轴][pmax t ≤W T 材料的许用切应力])[577.05.0(][σt -=对于塑性材料:])[0.18.0(][σt -=对于脆性材料:例2 实心等截面直轴,d=110mm ,(1) 试求截面Ⅱ上距轴线40mm 处的点的剪应力。
(2) 若已知[τ]=40MPa ,试校核轴的强度。
解:由扭矩图得知T 2=9.56kN.m(1)应力计算p2I T ρτρ⋅=MPa 6.2632/10110π104095601243=⨯⨯⨯⨯=--(2) 强度计算MPa 6.3616/10110π9560W T τ93t max max =⨯⨯==-<[τ]轴的强度满足危险横截面在AC 段,T max =9.56kN.m例3(同例2)若AD 轮互换位置,试校核轴的强度。
解:互调AD 轮位置后,扭矩图如图所示:]τ[MPa 60.8W T τmax max >==t ∴强度不符合要求。
T max =15.9 kN.m)1(16DW 43t απ-⋅=例4(同例2)若BD 轴改用内外径之比为9:10的空心轴,在保证同样强度条件下,试确定空心轴的内外径d 与D ;并计算空心与实心轴的材料消耗之比。
解:MPa 6.36max =t mkN T ⋅=56.9max t max max W T =t 由得mm T D 157)1(163max4max =⋅-⋅=t απd=0.9D=141mm235.04/4/)(2122=⋅-==d d D A A V V ππ实空实空例5 图示阶梯状圆轴,AB 段直径d 1=120mm ,BC 段直径d 2=100mm 。
扭转力偶矩M A =22 kN •m ,M B =36 kN •m ,M C =14 kN •m 。
材料的许用切应力[t ] = 80MPa ,试校核该轴的强度。
解:1、求内力,作出轴的扭矩图2214T 图(kN·m )M A M B ⅡⅠM C A CBBC 段()MPa 3.71mm 10016πmm N 1014362p 2max ,2=⋅⨯==W T t AB 段1p 1max ,1W T =t 2、计算轴横截面上的最大切应力并校核强度()MPa 8.64mm 12016πmm N 102236=⋅⨯=MPa 80][=<t 即该轴满足强度条件。
2214T 图(kN·m )讨论:扭矩合理分配M A M B ⅡⅠM CA CB M A ⅡⅠM BA C M CB 22143614一定使轴上的T max 最小例:某传动轴,传递扭转力偶矩M e =1.5kNm ,许用应力[τ]=50MPa 。
试按下列两种方案确定轴的截面尺寸,并比较其重量.(1)实心圆截面轴(2)空心圆截面轴Ⅱ(a = d 2/D 2 =0.9)(a)M e M ed 1lⅠM e(b)M elⅡD 2][1631111max ,1t t ≤===d M W M W T πe p e p ()][116432222max ,2t αt ≤-===D M W M W T πe p e p 解:1 确定实心轴的直径mm m M d e 5.530535.0105014.3105.116][1636331==⨯⨯⨯⨯=≥t π2 确定空心轴的内外径mmm M D e 3.760763.01050)9.01(14.3105.116])[1(163643342==⨯⨯-⨯⨯⨯=-≥t απmmd mm D 68,7622==mmd 541=两轴的重量比1212A A W W =可见空心圆轴的自重比实心圆轴轻。
()()2122221222214π4πd D d d D α-=-=讨论:为什么说空心圆轴比实心圆轴更适合于做受扭构件?395.0546876222=-=例圆柱螺旋弹簧如图(簧杆斜度 < 5°) 受轴向压力(拉力) F作用。
已知:簧圈平均半径R,簧杆直径d,弹簧的有效圈数n,簧杆材料的切变模量G,且簧圈平均直径D >> d。
试推导弹簧的应力和变形计算公式。
解:1、求簧杆横截面上的内力FF =S 剪力2DFT =扭矩分离体的平衡2、求簧杆横截面上的应力3328162d FD d DF W T ππt ===p maxa) 剪力相应的切应力(假定均匀分布)b)扭矩相应的切应力214d FA F s πt ==OTAD >> d 时略去簧圈的曲率影响)21(8162433221max D d d FD d D F d F +=+=+=πππt t t max38dFD πt =max OTA§4-5 等直圆轴扭转时的变形•刚度条件Ⅰ、扭转时的变形——两个横截面的相对扭转角j扭转角沿杆长的变化率pGI Tx =d d j xGI T d d p=j 相距d x 的微段两端截面间相对扭转角为M eM ejd j gD'T T O 1O 2ab abd xD A距离为L 的两个横截面之间的相对转角则为:dxG I T L 0P⎰=Φ1)若两截面之间扭矩的值不变,且轴为等直杆2)若两截面之间扭矩的值发生变化,或者轴为阶梯杆PG I T L =Φ(单位:rad)∑=⋅⋅=Φn1i Pii ii I G L T (单位:rad)Ⅱ、刚度条件][max θθ≤等直圆杆在扭转时的刚度条件:][max max θθ≤⨯=π180p GI T 对于精密机器的轴对于一般的传动轴m/30.0~15.0][ο≈θ常用单位:︒/mm/2][ο≈θ例5(同例2)d=110mm ,若各轮之间距离均为l =2m ,G=80GPa ,[ θ]=0.5°/m ,(1)计算相邻两轮之间的扭转角和轴两端截面之间的相对扭转角。