扭转变形

第九章扭转§9-1 引言工程问题中，有很多杆件是受扭转的。

自行车的中轴受扭转。

齿轮传动示意图圆杆各横截面绕杆的轴线作相对转动受力特点：圆截面直杆受到一对大小相等、转向相反、作用面垂直于杆的轴线外力偶作用（矢量与轴线一致）变形特点：M eM e 工程中主要承受扭转的构件称为“轴”，实际构件工作时除发生扭转变形外，还常伴随有弯曲、拉压等其他变形形式。

扭力偶：使杆产生扭转变形的外力偶M e扭转角：轴的变形以横截面间绕轴变形的相对角位移。

§9-2 动力传递与扭矩Ⅰ、传动轴的外力偶矩传动轴的转速n ；所传递的功率P (kW)作用在该轮上的外力偶矩M e 。

已知：求：传动轮的转速n 、功率P 及其上的外力偶矩M e 之间的关系：)(n P 0247M e m N ⋅=(P —马力)M eM e A B min)/()(9549r n kW P M e =ωM P =ωPM =Ⅱ、扭矩及扭矩图圆轴受扭时其横截面上的内力偶矩称为扭矩，用符号T 表示。

eM T =11利用截面法来确定.扭矩的符号规定按右手螺旋法则确定:扭矩矢量离开截面为正，指向截面为负。

仿照轴力图的做法，可作扭矩图，表明沿杆轴线各横截面上扭矩的变化情况。

e M T =11T T M eM e A B11BM e AM e 11x M e T 图+x T例1: 一传动轴如图，转速n = 300r/min；主动轮输入的功率P1= 500kW，三个从动轮输出的功率分别为：P2= 150kW，P3= 150kW，P4= 200kW。

试作轴的扭矩图。

首先必须计算作用在各轮上的外力偶矩mkN 9.15m N )3005009549(1⋅=⋅×=M mkN 78.4m N )3001509549(32⋅=⋅×==M M mkN 37.6m N )3002009549(4⋅=⋅×=M 解：221133M 1M 2M 3M 4ABCD分别计算各段的扭矩mkN 78.421⋅−=−=M T mkN 37.643⋅==M T 221133M 1M 2M 3M 4A B CDT 111xM 2AT 2AM 2BM 322xT 333DM 4x2239.56kN mT M M =−−=−⋅扭矩图T max = 9.56 kN·m在CA 段内M 1M 2M 3M 4ABCD 4.789.566.37T 图(kN·m)一、扭转试验与假设：§9-3 切应力互等定理与剪切胡克定律1、相邻圆周线绕杆的轴线相对转动，但圆周的大小、形状、间距都未变；（各横截面如同刚性圆片）2、纵向线倾斜了同一个角度γ ，表面上所有矩形均变成平行四边形。

第四章 扭转4.1预备知识一、基本概念 1、扭转变形扭转变形是杆件的基本变形之一，扭转变形的受力特点是：杆件受力偶系的作用，这些力偶的作用面都垂直于杆轴。

此时，截面B 相对于截面A 转了一个角度ϕ，称为扭转角。

同时，杆件表面的纵向直线也转了一个角度γ变为螺旋线，γ称为剪切角。

2、外力偶杆件所受外力偶的大小一般不是直接给出时，应经过适当的换算。

若己知轴传递的功率P(kW)和转速n(r/min)，则轴所受的外力偶矩)(9549Nm nPT =。

3、扭矩和扭矩图圆轴扭转时，截面上的内力矩称为扭矩，用T 表示。

扭矩的正负号，按右手螺旋法则判定。

如扭矩矢量与截面外向法线一致，为正扭矩，反之为负；求扭矩时仍采用截面法。

扭矩图是扭矩沿轴线变化图形，与轴力图的画法是相似4、纯剪切 切应力互等定理单元体的左右两个侧面上只有切应力而无正应力，此种单元体发生的变形称为纯剪切。

在相互垂直的两个平面上，切应力必然成对存在且数值相等，两者都垂直于两个平面的交线、方向到共同指向或共同背离积这一交线，这就是切应力互等定理。

5、切应变 剪切虎克定律 对于纯剪切的单元体，其变形是相对两侧面发生的微小错动，以γ来度量错动变形程度，即称切应变。

当切应力不超过材料的剪切比例极限时，切应力τ和切应变γ成正比，即τ=G γG 称材料的剪切弹性模量，常用单位是GPa 。

6、圆杆扭转时的应力和强度计算(1) 圆杆扭转时，横截面上的切应力垂直于半径，并沿半径线性分布，距圆心为ρ处的切应力为ρτρpI T =图式中T 为横截面的扭矩，I p 为截面的极惯性矩。

(2) 圆形截面极惯性矩和抗扭截面系数实心圆截面324D I p π=， 163D W p π=（D 为直径） 空心圆截面)1(3244a D I p -=π， )1(1643απ-=D W p （D 为外径，d 为内径，D d /=α）(3)圆杆扭转时横截面上的最大切应力发生在外表面处tW T =max τ 式中W t =I p /R ，称为圆杆抗扭截面系数（或抗抟截面模量）。

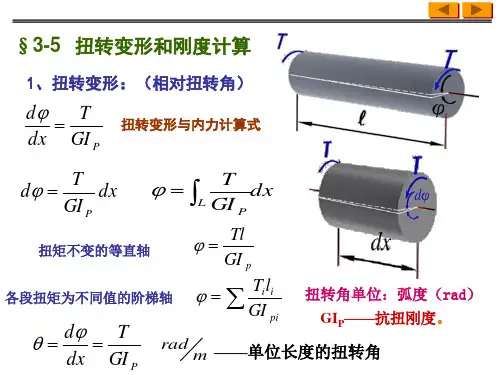
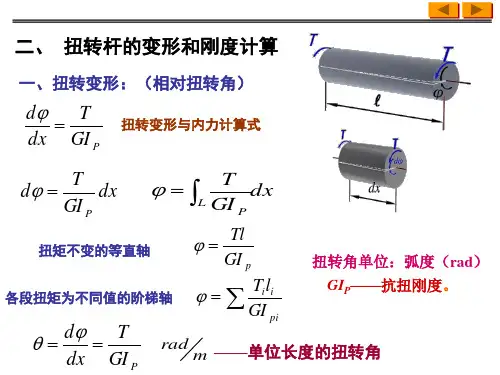
材料力学中的四种基本变形举例
1.拉伸变形：
拉伸变形是指在外力的作用下，物体的长度增加或变长的过程。

这种
变形常见于拉伸试验中的拉力加载中，例如在拉伸试验机上施加外力，拉
伸材料直至材料的断裂点。

一个常见的例子是橡皮筋，当我们拉伸橡皮筋时，它的长度会增加。

2.压缩变形：
压缩变形是指在外力的作用下，物体的长度减少或变短的过程。

这种
变形常见于承受压力的构件中，例如梁柱结构承受竖向荷载时会产生压缩
变形。

一个典型的例子是弹簧，当我们用力将弹簧压缩时，它的长度会变短。

3.剪切变形：
剪切变形是指在外力的作用下，物体的平行侧面发生相对位移的过程。

这种变形常见于切削和金属加工中，例如在使用剪切机切割金属板材时，
金属板材的平行侧面会产生相对的移动。

另一个例子是在泥土工程中，当
土壤受到剪切力时，会发生剪切变形。

4.扭转变形：
扭转变形是指在外力作用下，物体沿纵轴发生旋转的过程。

这种变形
常见于旋转机械中，例如在使用螺旋桨驱动船只前进时，船体会发生扭转
变形。

另一个例子是在汽车悬挂系统中，当车辆转弯时，车身会发生扭转
变形。

这四种基本变形在材料力学中都具有重要的意义，并广泛应用于工程设计和材料选型过程中。

通过对这些变形的认识和理解，我们能够更好地预测和控制材料的行为和性能。

第三章 扭转变形授课学时：6学时 内容：外力偶矩的计算； 扭转剪应力推导过程；圆轴扭转时横截面上剪应力分布规律和强度，圆轴扭转变形时的刚度和变形（相对扭转角）计算。

$3.1 扭转的概念1．外力特征力偶矩矢平行于杆的轴线。

力偶矩矢方向按右手螺旋法则确定。

2．扭转变形受力特点杆件的两端作用着大小相等，方向相反，且作用面垂直于杆件轴线。

3．力偶变形特点各轴线仍为直线，杆件的任意两个横截面发生绕轴线的相对转动。

A B4．工程实例方向盘轴、传动轴。

$3.2扭矩和扭矩图1．外力偶矩的计算).(9549m N nNm ⋅= N ：功率；n ：转速 2．扭矩和扭矩图（1）内力偶矩：杆件受扭时截面上的内力偶矩。

符号T （2）内力偶矩计算—截面法用截面n n -将轴分成两部分，按右手螺旋法则把m ，T 表示为矢量，列出左部分平衡方程0=∑xM，得到m T =当矢量方向与截面外法线方向一致时，T 为正；反之为负。

对于杆件一侧作用多个外力偶矩情况，任一截面的内力偶矩等于其一侧所有外力偶矩的代数和∑=i M T（3）扭矩图表示杆件各横截面上扭矩变化规律的图形，反应出maxT值及其截面位置，从而进行强度计算（危险截面）。

该图一般以杆件轴线为nT横轴表示横截面位置，纵轴表示扭矩大小。

例 传动轴如图，主动轮A 输出功率kW P A 36=，从动轮B 、C 、D 输出功率分别为kW P P C B 11==，kW P D 14=，轴的转速为min /300r n =。

试作轴的扭矩图。

解：（1）求外力偶矩m N n P m A A .11463003695499549=⨯== m N n P m m B C B .3503001195499549=⨯===m N n P m D D .4463001495499549=⨯==（2）求截面内扭矩 在BC 段内01=+B m Tm N m T B .3501-=-=在CA 段内0=++B C m m Tm N m m T B C .700-=--=在AD 段内m N m T D .446==III（3）画扭矩图$3.3薄壁圆筒的扭转1．薄壁圆筒的扭转实验A mB mC m Dm B C ADI III IIIIIIII B m 1T B m C mT T IIIDm Tx(a)(c)(e)试验前后比较现象：①圆筒表面的各圆周线的形状、大小和间距均未改变，只是绕轴线作了相对转动。

扭转的变形特点
扭转是一种物体在应力作用下发生的变形。

它具有以下特点：
1. 扭转变形是围绕物体的轴线进行的旋转变形，相对于其他形式的变形（如拉伸、压缩等），扭转变形是围绕一个中心轴线进行的。

2. 扭转变形产生的应力和应变分布不均匀，最大的应力出现在物体的表面附近，随着距离表面的增加而逐渐减小。

3. 扭转变形会引起物体的截面形状发生改变，原本圆形的截面可能会变成椭圆形或者其他形状。

4. 扭转变形会导致物体长度的变化，但总长度保持不变。

例如，在扭转过程中，物体的一部分可能会延长，而另一部分则会缩短。

5. 扭转变形通常发生在柔性材料上，如金属、塑料等。

刚性材料由于其高强度和低可变形性质，往往不容易发生明显的扭转变形。

这些特点使得扭转变形在许多工程领域中具有重要的应用，如机械设计、结构工程等。

1。