小柔度杆9-4欧拉公式的应用范围经验公式
- 格式:ppt
- 大小:1.16 MB
- 文档页数:32


欧拉公式及其应用
欧拉公式是数学中的一条重要定理,被誉为数学中的“五角星
公式”。
它由瑞士数学家欧拉于1736年发现,形式为V-E+F=2。
其中,V表示多面体的顶点数,E表示多面体的边数,F表示多面
体的面数。
欧拉公式一般只用于欧几里得空间中的凸多面体,然而,它的
应用却不仅限于此。
在计算机图形学中,欧拉公式已经成为了一
个广泛使用的工具,可以用于计算各种复杂的图形的拓扑结构信息。
此外,在数学、力学、物理学中,欧拉公式也有着广泛的应用。
在数学中,它被广泛应用于代数拓扑、流形拓扑等领域,是许多
数学问题的重要手段。
在力学中,欧拉公式被用来证明固体力学
基本方程组的平衡条件;在物理学中,则被用于推导色散关系、
介质常数等常见物理量。
在计算机科学领域,欧拉公式也是一个非常有用的工具。
例如,在计算机图形学中,我们常常需要将一幅图像转换成由多边形拼
接而成的图形,而欧拉公式就是用来计算这些多边形的顶点、边
和面的个数的。
此外,在计算机网络领域中,欧拉公式也被广泛运用于网络拓扑的计算和分析。
总之,欧拉公式作为数学中的一条重要定理,不仅仅在几何学中有着广泛的应用,还在代数拓扑、流形拓扑、计算机图形学、力学、物理学等领域中发挥着不可替代的作用。
研究欧拉公式及其应用,不仅对求解实际问题有着重要的帮助作用,还对我们深入理解数学的本质和发展历程有着重要的启示作用。

欧拉公式的适用范围经验公式一、临界应力A l EI A F σ22cr cr )(πμ==I i A=令 , i :惯性半径 令 ,λ:压杆的柔度(长细比)。
i lμλ=()(/)22222ππE E i l l i μμ=⋅=22πE λ=二、 欧拉公式的适用范围或 =≤2cr p 2πE σσλ=1pπE σλ≥2p πE σλ令 λ ≥ λ1的杆称为大柔度压杆或细长压杆。
当 λ<λ1 但大于某一数值 λ2的压杆不能应用欧拉公式,此时需用经验公式。
Q235钢,取 E =206GPa ,σp =200MPa ,得916p 20610ππ10020010E σλ⨯==≈⨯三. 常用的经验公式式中:a 和b 是与材料有关的常数,可查表。
直线公式 s cr σλ≤-=b a σ 的杆为中柔度杆,其临界应力用经验公式计算。
12λλλ<≤或 ba s σλ-≥ba s σλ-=2令1λλ≥12λλλ<≤四、压杆的分类及临界应力总图1.压杆的分类2cr 2πE σλ=λb a σ-=cr scr σσ=(1)大柔度杆 (2)中柔度杆 (3)小柔度杆 2λλ≤2.临界应力总图 s cr σσ=λb a σ-=cr 22cr πλE σ=crσλλ1 λ2 p σsσ例题压杆截面如图所示。
两端为柱形铰链约束,若绕y 轴失稳可视为两端固定,若绕z轴失稳可视为两端铰支。
杆长l=1m,材料的弹性模量E=200GPa,p=200MPa。
求压杆的临界应力。
30mm yz解: ==1p π99E σλ31(0.030.02)120.0058m 0.030.02y y I i A=⨯==⨯30mm y z m 0087.0==AI i z z15.0==z y μμ11586====z z z y y y i l i lμλμλλz > λy ,所以压杆绕 z 轴先失稳, 且 λz =115 > λ1,用欧拉公式计算临界力。



细长压杆的临界⼒公式—欧拉公式.10.2 细长压杆的临界⼒公式—欧拉公式⼀、两端铰⽀压杆的临界⼒图9—4为两端受压杆件,⼈们经过对不同长度(l ),不同截⾯(I ),不同材料(E )的压杆在内⼒不超过材料的⽐例极限时发⽣失稳的临界⼒P cr 研究得知: 22lPcr EI=π(9—1)式中:π—圆周率;E —材料的弹性摸量;l —杆件长度;I —杆件截⾯对⾏⼼主轴的惯性矩。
图9-4当杆端在各⽅向的约束情况相同时,压杆总是在抗弯刚度最⼩的纵向平⾯内失稳,所以(9-1)式中的惯性矩应取截⾯最⼩的形⼼惯性矩I min 。
瑞⼠科学家欧拉(L.Eular )早在18世纪,就对理想细长压杆在弹性范围的稳定性进⾏了研究。
从理论上证明了上述(9-1)式是正确的,因此(9-1)式⼜称为计算临界⼒的欧拉公式。
⼆、杆端⽀承对临界⼒的影响图9-5(a)(b)(c)(d)⼯程上常见的杆端⽀承形式主要有四种,如图9-5所⽰,欧拉进⼀步研究得出各种⽀承情况下的临界⼒。
如⼀端固定,⼀端⾃由的杆件,这种⽀承形式下压杆的临界⼒,只要在(9-1)式中以2l 代替l 即可。
()222l P cr EI=π(a )同理,可得两端固定⽀承的临界⼒为()225.0l P cr EI=π(b )⼀端固定,⼀端铰⽀压杆的临界⼒为 ()227.0l P cr EIπ(c )式(a ),(b),(c)和(9-1)可归纳为统⼀的表达式()22l P cr µπEI = (9-2)式中l µ称为压杆计算长度,µ称为长度系数,⼏种不同杆端⽀承的各µ值列于表9—1中,µ反映了杆端⽀承情况对临界⼒的影响。
表9-1 各种杆端⽀承压杆的长度系数图例9.1 图⽰轴⼼受压杆,截⾯⾯积为10mm ?20mm 。
已知其为细长杆,弹性模量E=200GPa ,试计算其临界⼒。
2m20图9-6单位:mm解:由杆件的约束形式可知:7.0=µ4333min1067.112102012mm hb I I y ?=?===临界⼒:223320010 1.67101076.2 1.076()(0.7 2.510)cr EI P N kN l ππµ====?? 三、临界应⼒和柔度在临界⼒的作⽤下,细长压杆横截⾯上的平均应⼒叫做压杆的临界应⼒,⽤cr σ表⽰。




材料力学在工程中的实际应用目录一、关于拉伸或压缩的强度设计 (2)二、圆轴扭转时轴截面尺寸的设计 (5)1、圆轴扭转时,横截面上的内力偶矩——扭矩 (6)2、圆轴扭转的时候,横截面上的应力、强度条件 (7)3、圆轴扭转时的变形,刚度条件 (8)三、矩形横截面弯曲梁的bxh设计 (9)1、梁的正应力、正应力强度条件 (9)2、梁的切应力、切应力强度条件 (11)四、扭转和弯曲的组合变形轴的设计 (12)五、压杆稳定性校核方面问题 (13)1、弹性平衡稳定性的概念 (13)2、细长压杆临界载荷的欧拉公式 (14)3、三类压杆的临界载荷 (14)4、压杆稳定校核. (15)5、如何提高压杆的稳定性 (16)材料力学在工程中的实际应用材料力学是一门研究构件承载能力的学科。
作为土木建筑类的三大基础学科之一,材料力学是设计工业设施必须掌握的知识。
而在本学期的课程中,我不仅在老师的带领下学到了本学科的内容,更深刻了解到了本学科的严谨和重要性。
材料力学在生活中的应用非常广泛,大到机械中的各种机器建筑中的各个结构,小到生活中的日用产品。
各种物件都要符合它的强度和刚度以及稳定性要求才能够正常工作、保证使用者的安全。
而生活中机械常用的连接件如铆钉、键、销钉、螺栓等的变形均属于剪切变形,在设计时应主要考虑其剪切应力;汽车的传动轴、转向轴的变形则属于扭转变形;火车轴和起重机大梁的变形属于弯曲变形。
但是,往往在我们设计的时候需要同时考虑几个方面的变形,比如说在车床工作的时候,同时发生了扭转、弯曲和压缩三种基本变形。
材料力学在工程中常常会遇到的问题有:一、关于拉伸或压缩的强度设计拉伸和压缩是杆件基本受力与变形形式中最简单的一种,所涉及的一些基本原理和方法也都相对简单,但是在材料力学中有一定的普遍意义。
举例:(1)一些机器和结构中所用到的各种紧固螺栓,在紧固的时候,要对螺栓市价预紧力,螺栓承受轴向拉力就会发生伸长变形(2)斜拉桥承受拉力的钢缆以上这些举例均为轴向拉伸和压缩的日常实例,而我们在解决问题时,通常会将实物简化为如下形式:这样不仅让问题看起来更简单、更直观,也便于将应力的计算最简化,免于误算漏算多算等情况。
材料力学笔记之——欧拉公式适用范围、临界应力总图欧拉公式的适用范围欧拉公式的推导方法是,在服从胡克定律的前提下,得到梁的曲率方程,再由曲率方程推导出挠曲线近似微分方程,挠曲线微分方程积分并根据边界条件确定积分常数,从而确定压杆的临界压力。
综上所述,欧拉公式只有在弹性范围内才是适用的,杆内的应力小于比例极限。
压杆在临界压力作用下,其在直线平衡位置时横截面上的应力称为临界应力。
其中式中,λ称为柔度(长细比),i为截面的惯性半径。
柔度又称为压杆的长细比,反映了压杆长度、约束条件、截面尺寸和形状对临界力的影响。
由欧拉公式的推导过程可知,欧拉公式的适用范围,临界应力小于或等于材料的比例极限可得这类杆件称为大柔度杆,或细长杆。
经验公式、临界应力总图当杆件的柔度小于λp时,临界应力大于材料的比例极限,欧拉公式不再适用。
对于这类杆件工程中一般使用以试验为依据的经验公式:直线公式、抛物线公式。
1. 直线公式这类压杆失稳时,横截面上的应力已超过比例极限,故属于弹塑性稳定问题,直线公式,即临界应力与柔度成线性关系,且临界应力随柔度增大而减小式中,a、b为与材料性能有关的常数。
当应力增大到屈服极限时,材料发生屈服失效,这时不再是稳定问题,而是强度问题,其临界应力最大值为可得直线公式适用的柔度下限值即直线公式适用的柔度范围这类杆件称为中柔度杆件。
当杆件的柔度小于λs时,称为小柔度杆或短粗杆。
这类压杆发生强度失效,而不是稳定失效,临界应力临界应力随柔度变化的关系,可画出曲线如下图所示,称为压杆的临界应力总图。
临界应力总图(直线公式)2. 抛物线公式对于中柔度杆和小柔度杆,不同的工程设计中,也可以采用抛物线公式计算临界应力式中,a1 和b1 也是与材料有关的常数。
临界应力总图(抛物线公式)折减弹性模量理论工程中大部分受压杆件不是大柔度杆件,可以采用折减弹性模量理论分析这类压杆的临界压力。
材料在压缩时的应力-应变曲线如图所示,当应力超过比例极限时,加载时应力应变曲线为非线性,把这部分曲线的切线斜率作为该应力水平的弹性模量,称为切线弹性模量。
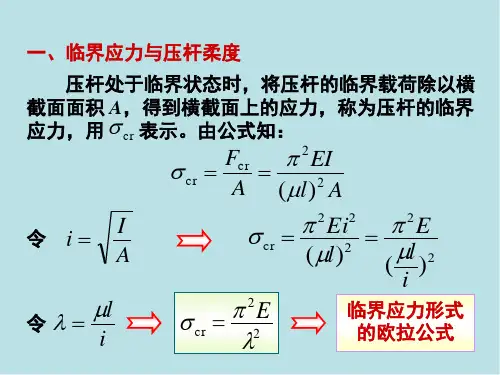
第二节压杆件的临界应力
一、临界应力
设压杆的横截面面积为A,则压杆的临界应力为
将压杆截面的惯性半径
代入上式得
令
有
上式称为压杆临界应力欧拉公式,其中λ称为压杆的柔度。
二、欧拉公式的适用范围
欧拉公式只有压杆的临界应力不超过材料的比例极限时才成立,即材料处于弹性变形范围
或
上式表明,欧拉公式的适用范围是压杆的柔度必需大于最小柔度λp即,满足这一条件的压杆称为大柔度杆(或细长压杆)。
三、超过比例极限时的临界应力
工程中中有许多压杆,其柔度λ往往小于λp,这类压杆称为中、小柔度杆。
其常用抛物线公式,即对于钢材
对于铸铁
四、临界应力总图
压杆的临界应力是其柔度λ的函数,其函数图象称为临界应力总图。
如下Q235钢的临界应力总图
其中临界应力公式分界点为
——应用欧拉公式
工程上以λc作为分界点,这是由于在实际工程中,压杆所受的压力
存在偏心等缘故。