当前位置：文档之家 › 材料力学第12章 压杆稳定

材料力学第12章 压杆稳定

  • 格式：ppt
  • 大小：844.00 KB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

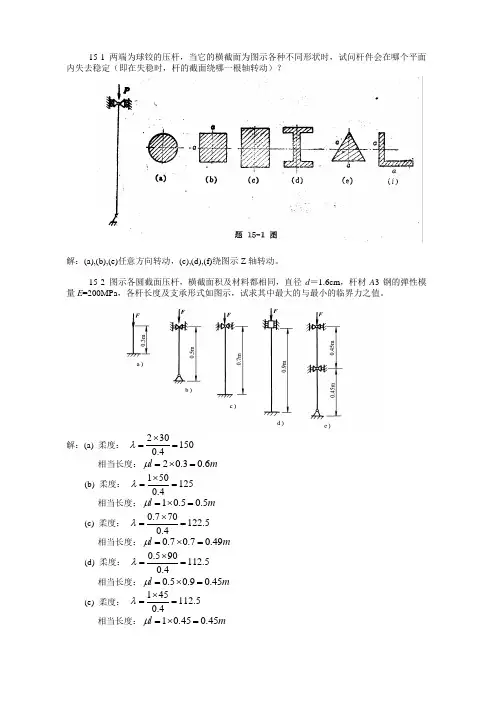
材料力学答案- 压杆稳定

材料力学答案- 压杆稳定

15-1 两端为球铰的压杆，当它的横截面为图示各种不同形状时，试问杆件会在哪个平面内失去稳定（即在失稳时，杆的截面绕哪一根轴转动）？解：(a),(b),(e)任意方向转动，(c),(d),(f)绕图示Z 轴转动。

15-2 图示各圆截面压杆，横截面积及材料都相同，直径d ＝1.6cm ，杆材A 3钢的弹性模量E =200MPa ，各杆长度及支承形式如图示，试求其中最大的与最小的临界力之值。

解：(a) 柔度： 2301500.4λ⨯== 相当长度：20.30.6l m μ=⨯=(b) 柔度： 1501250.4λ⨯== 相当长度：10.50.5l m μ=⨯=(c) 柔度： 0.770122.50.4λ⨯== 相当长度：0.70.70.49l m μ=⨯=(d) 柔度： 0.590112.50.4λ⨯== 相当长度：0.50.90.45l m μ=⨯=(e) 柔度： 145112.50.4λ⨯== 相当长度：10.450.45l m μ=⨯=由E=200Gpa 及各柔度值看出：各压杆的临界力可用欧拉公式计算。

即：()22cr EIF l πμ=各压杆的EJ 均相同，故相当长度最大的压杆(a)临界力最小，压杆(d)与(e)的临界力最大，分别为：()2948222320010 1.610640.617.6410cr EFF l N πππμ-⨯⨯⨯⨯⨯===⨯()2948222320010 1.610640.4531.3010cr EIF l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材P σ=230MPa ，s σ=274MPa ，E =200GPa ，直线公式λσ22.1338-=cr ，试计算该材料压杆的P λ及S λ值，并绘制1500≤≤λ范围内的临界应力总图。

解：92.633827452.5p s s a λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆，其外径和内径分别为，12mm 和10mm ，杆长为383mm ，两端为铰支座，材料的E ＝210GPa ，P σ=288MPa ，试求此挺杆的临界力cr F 。

【最新精选】压杆稳定实验报告

【最新精选】压杆稳定实验报告

浙江大学材料力学实验报告（实验项目：压杆稳定）一、实验目的：1、观察压杆的失稳现象；2、测定两端铰支压杆的临界压力；3、观察改变支座约束对压杆临界压力的影响。

二、设备及装置：1. 带有力传感和显示器的简易加载装置或万能电子试验机；2. 数字应变仪；3. 大量程百分表及支架；4. 游标卡尺及卷尺；5. 试样，压杆试样为由弹簧钢制成的细长杆，截面为矩形，两端加工成带有小圆弧的刀刃。

在试样中点的左右两端各贴仪枚应变片。

6. 支座，支座为浅V 性压杆变形时两端可绕Z 轴转动，故可作为铰支架。

三、实验原理和方法：1、理论计算：理想压杆，当压力P 小于临界压力cr P 时，压杆的直线平衡是稳定的。

这时压力P 与中点挠度δ的关系相当于右图中的直线OA 。

当压力到达临界压力cr P 时，压杆的直线平衡变为不稳定，它可能转为曲线平衡。

按照小挠度理论，P 与δ的关系相当于图中水平线AB 。

两端铰支细长杆的临界压力由欧拉公式计算 2cr 2P EIl π=，其中I 为横截面对z 轴的惯性矩。

2、实测时：实际压杆难免有初弯曲，材料不均匀和压力偏心等缺陷，由于这些缺陷，在P 远小于cr P 时，压杆已经出现弯曲。

开始，δ很不明显，且增长缓慢，如图中的OCD 段。

随着P 逐步接近cr P ，δ将急剧增大。

只有弹性很好的细长杆才可以承受大挠度，压力才可能略微超过cr P ，实测时，在压杆两侧各贴一应变片，测定P-ε曲线，对前后应变ε取增量ε∆，当ε∆大于上一个的ε∆的2倍时即认为此时的压力为临界压力。

3、加载分两个阶段，在理论值cr P 的70%~80%之前，可采取大等级加载，载荷超过cr P 的80%以后，载荷增量应取得小些。

在整个实验过程中，加载要保持均匀、平稳、缓慢。

四、实验结果1、理论计算参数记录：b=30.00mm, h=3.50mm, k=2.13, L=525mm, E=210GPa31041.07191012bh I m -==⨯，则由欧拉公式得 2cr 2P 805.2EI N lπ== 2、实测临界压力：实验数据记录如下：压力-800N 时，应变增量192，超过了-780N 时的应变增量90的2倍，可得临界压力为-800N 。

直梁的弯曲及组合变形与压杆稳定——教案

直梁的弯曲及组合变形与压杆稳定——教案

直梁的弯曲及组合变形与压杆稳定——教案一、教学目标：1. 让学生了解直梁弯曲的基本概念，掌握梁弯曲的弹性理论。

2. 使学生理解组合变形及压杆稳定的基本原理，能够分析实际工程中的相关问题。

3. 培养学生的动手实践能力，通过实例分析提高学生解决工程问题的能力。

二、教学内容：1. 直梁弯曲的基本概念：直梁、弯曲、剪力、弯矩等。

2. 梁弯曲的弹性理论：弯曲应力、弯曲变形、弯曲强度计算等。

3. 组合变形：拉伸、压缩、弯曲、剪切等组合变形的分析方法。

4. 压杆稳定的基本原理：压杆稳定条件、压杆失稳现象、压杆稳定计算等。

5. 实例分析：分析实际工程中的直梁弯曲、组合变形与压杆稳定问题。

三、教学方法：1. 采用讲授与讨论相结合的方式，让学生掌握直梁弯曲及组合变形与压杆稳定的基本理论。

2. 通过案例分析，使学生能够将理论知识应用于实际工程问题。

3. 利用动画、图片等辅助教学手段，帮助学生形象地理解抽象的概念。

4. 安排课堂讨论，鼓励学生提问、发表观点，提高学生的参与度。

四、教学安排：1. 课时：本章共计12课时。

2. 教学方式：讲授、案例分析、课堂讨论。

3. 教学进程：第1-4课时：直梁弯曲的基本概念及弹性理论。

第5-8课时：组合变形及压杆稳定的基本原理。

第9-12课时：实例分析及练习。

五、教学评价：1. 课堂表现：观察学生在课堂上的参与程度、提问回答等情况，给予相应的表现评价。

2. 课后作业：布置相关练习题，检验学生对知识的掌握程度。

3. 课程报告：要求学生选择一个实际工程案例进行分析，报告应包括问题分析、计算过程和结论。

通过课程报告评价学生的实践能力。

4. 期末考试：设置有关直梁弯曲、组合变形与压杆稳定的题目，考察学生的综合运用能力。

六、教学资源：1. 教材：《材料力学》、《结构力学》等相关教材。

2. 辅助材料：PPT课件、动画、图片、案例资料等。

3. 实验设备：力学实验仪、弯曲实验装置、压杆实验装置等。

4. 网络资源：相关学术期刊、在线课程、论坛等。

材料力学压杆稳定概念欧拉公式计算临界力

材料力学压杆稳定概念欧拉公式计算临界力

材料力学压杆稳定概念欧拉公式计算临界力材料力学是研究物体受力及变形行为的一门学科。

压杆稳定是材料力学中重要的概念之一、当一个杆件受到作用力时，如果杆件不发生任何形状上的变化，我们称之为杆件处于稳定状态。

然而，当作用力超过一定临界值时，杆件就会发生失稳，产生形状上的变化。

因此，欧拉公式就是用来计算杆件临界力的一种方式。

欧拉公式由瑞士数学家欧拉于18世纪中叶首次提出。

它的基本假设是杆件是理想化的，即杆件是均匀、无缺陷、具有均匀截面的杆件。

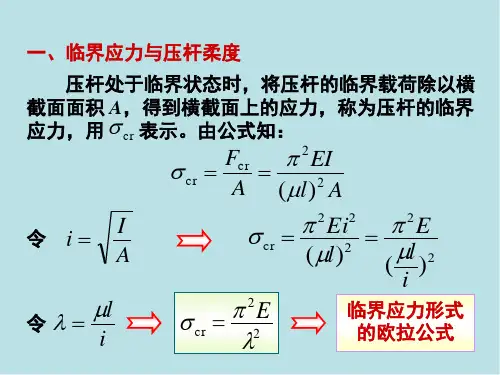
根据欧拉公式，杆件临界力可通过以下公式计算：Pcr = (π^2 * E * I) / L^2其中，Pcr表示临界力，E表示杨氏模量，I表示截面惯性矩，L表示杆件的有效长度。

从上述公式中可以看出，临界力与材料的弹性模量有关，即材料越硬，临界力越大；同时临界力与截面的形状也有关，即截面惯性矩越大，临界力越大；临界力还与杆件长度有关，即杆件越短，临界力越大。

例子：假设有一根长为L的无缺陷的圆柱形杆件，其截面半径为r，杨氏模量为E。

根据材料力学的知识，该圆柱形杆件的截面惯性矩可计算为I=(π*r^4)/4Pcr = (π^2 * E * ((π * r^4) / 4) ) / L^2通过上述公式，可以计算出该无缺陷的圆柱形杆件的临界力。

这个临界力表示了该杆件能够承受的最大作用力。

如果作用力超过了临界力，该杆件将发生失稳，产生形状上的变化。

总结起来，材料力学中的压杆稳定概念是指杆件在受力作用下不发生形状上的变化。

欧拉公式是用来计算杆件临界力的一种常用公式，可以帮助工程师们确定杆件的最大承载能力。

材料力学压杆稳定第3节 欧拉公式及经验公式

材料力学压杆稳定第3节 欧拉公式及经验公式



2E 12


2
206109 1602
79.3 MPa
Fcr1 cr1A 79.3106 0.00785N 623 kN
（b）第二根压杆的临界载荷
2

l2
i

21 0.025
80
60 P 100
60 P 100 该杆为中柔度压杆，用直线公式求：
cr S
cr (a b)
cr

2E 2
根据欧拉公式与抛
物线经验公式，得
低合金结构钢等压
杆的 cr 总图。
S
P

2、抛物线型经验公式
在工程实际中，对于中、小柔度压杆的临界应力计 算，也有建议采用抛物线型经验公式的，此公式为
cr a1 b12
式中 a1 、b1 与是与材料
cr?令令aii?aleiaf22crcr?????22222crilelei???????令令il???临界应力形式的欧拉公式22cr???e?式中柔度是一个无量纲的量它综合反映了压杆的长度杆端的约束以及截面尺寸对临界应力的影响
一、临界应力与压杆柔度
压杆处于临界状态时，将压杆的临界载荷除以横
截面面积 A，得到横截面上的应力，称为压杆的临界
式中 为具体压杆的柔度，a﹑b为与材料的力学
性能有关的常数，单位为 MPa。表 7-2 中列出了几
种常用材料的 a、b 值。
表 7-2 几种常用材料的 a、b 的值
材料
（强度极限 b/ MPa ） （屈服点 S /MPa ）
a
b
（MPa） （MPa）
P
S
Q235 钢( b 372 , S 235 ) 304 1.12 100
材料力学-压杆稳定

材料力学-压杆稳定


1．直线型经验公式
对于柔度(λs≤λ<λp)的中柔 度杆（中长压杆），临界应力 与λ的关系采用直线公式：
cr a b 13 8
式(13-8)中的系数a,b可查书中表 13-1。 λ的最低界限：
s
a
s
b
(塑性材料)
b
a
b
b
(脆性材料)
---------(13-9)
图13-3
2．抛物线型经验公式
式中有c1,c2,k三个未知量。根据边界条件：当x=0时， yA=0；代入式(c)得c2=0。式(c)成为
y c1 sinkx (d )
当x=l时，yB=0；代入式(d)后可得 c1 sinkl 0 (e)
要满足式(e)，必然是c1或sinkl等于零，若c1=0，则压杆 上各点的位移都为零，这显然与压杆在微弯状态下保持平衡 的前提不符，故必须是sinkl=0。要满足这一条件的kl值为：
kl 0, ,2 ,L ,n （n为正整数）
由k P n 可得：
EI l
P
n2 2 EI
l2
(
f
)
使压杆可能在微弯状态下保持平衡的最大轴向压力，应
该是式(f) 中n=1时的P值，这就是所求的两端铰支压杆的临
界力Pcr，即
Pcr
2 EI
l2
(13 1)
式(13-1)习惯上称为两端铰支压杆的欧拉公式。当各个 方向的支承情况相同时（如两端为球铰），压杆总是在它的 抗弯能力最小的纵向平面内失稳，所以式(13-1)中的EI是压 杆的最小抗弯刚度，即I应取截面的最小形心主惯性矩Imin。
2
图13-4 对于柔度(λ<λc)的杆件，临界应力与λ的关系采用抛物线公式：
材料力学压杆稳定概念欧拉公式计算临界力课件

材料力学压杆稳定概念欧拉公式计算临界力课件


杆的长度远大于横截面尺 寸，且横截面尺寸保持不 变。
杆的材料需满足胡克定律 ，即应力与应变成线性关 系。
欧拉公式在压杆稳定中的应用
01
通过欧拉公式，可以计算出压杆在临界状态下的临界力，即压杆失稳 前的最大承载力。
02
临界力的大小与压杆的材料、截面形状、尺寸等因素有关，是评估压 杆稳定性能的重要指标。
通过优化载荷分布，可以改善压杆的受力状态，从而提高稳定性。
THANKS
感谢观看
详细描述
理想压杆的临界力不受压杆重量和惯性影响，因此在实际应用中 ，需要考虑这些因素对临界力的影响。
实际压杆临界力计算
总结词
实际压杆是指考虑自身重量和惯 性影响的压杆，其临界力计算需 考虑这些因素。
总结词
实际压杆的临界力受到自身重量 和惯性影响，因此需要考虑这些 因素对临界力的影响。
详细描述
在计算实际压杆的临界力时，需 要考虑压杆自重产生的挠度以及 横截面面积和长度等因素的影响 。
02
推导过程中，考虑了压杆的弯曲变形和轴向压缩变形，利用能
量守恒和弹性力学的基本方程，最终得到了欧拉公式。
推导过程涉及了数学和物理的相关知识，需要一定的专业背景
03
和理论基础。
欧拉公式应用条件
欧拉公式适用于理想弹性 材料制成的细长等截面直 杆。
杆的受力方式为两端受压 ，且轴向压力逐渐增加直 到临界状态。
材料力学压杆稳定概念欧 拉公式计算临界力课件
• 压杆稳定概念 • 欧拉公式 • 临界力计算 • 压杆稳定性的影响因素 • 提高压杆稳定性的措施
01
压杆稳定概念
压杆失稳现象
01
02
03
弯曲变形
当压杆受到压力时，可能 会发生弯曲变形，导致承 载能力下降。
材料力学课件(压杆稳定性)

材料力学课件(压杆稳定性)


2 EI
2 a2
改变力F指向，BD成为压杆，临界压力
F2
2 EI
2a 2
Fcr
比较：Fcr Fcr
1 2 EI
2FAB FBD 2 a 2
例9-4.一端固定一端自由压杆，长为 l，弯曲刚度
为EI，设挠曲线方程
w
2l 3
(3lx 2
x3)
，为自由
端挠度。试用能量法去定临界压力的近似值。
思考： P 3169-4，习题9-11，13，14，18
练习： P 319习题9-10，12，15，17
（3）合理稳定性设计
[ ]st
与
L
i
成反比
合理截面：约束性质接近时，iminimax ——组合截面 提高 i ——使截面积远离形心
增强约束：缩短相当长度
思考：含有压杆的超静定问题
温度变化引起的稳定性问题
、[]st与 成反比
值：木杆——式（9 11，12）
钢杆——表 92，3
（2）稳定性条件
F A
[ ]st
[ ]
稳定性r 或 与 或 i 为非线性关系，选择截面
尺寸时需用迭代法
例9-5. Q235钢连杆，工字型截面A＝552mm2，Iz＝ 7.40×104mm4，Iy＝1. 41×104mm4，有效长度l＝ 580mm，两端柱形铰约束，xy平面失稳μz＝1，xz 平面失稳μy＝0.6，属 a 类压杆，轴向压力F＝35kN， [σ]＝206MPa。试求稳定许用应力，并校核稳定性。
思考：比较一根杆的柔度与柔度的界限值
影响大柔度、中柔度和小柔度杆临 界应力因素的异同
3. 压杆的稳定性条件与合理设计
（1）稳定许用应力
实际压杆与理想压杆的差异：初曲率、压力偏心、 材料缺陷等
材料力学 第十二章 压杆稳定

材料力学 第十二章 压杆稳定


P ≤ Pcr
(1) P ≤ Pcr
干扰力去掉后， 干扰力去掉后，杆件由微小弯曲回到 直线位置，恢复原有的平衡状态，称压杆 直线位置，恢复原有的平衡状态， 稳定平衡。 直线状态的平衡是稳定平衡 直线状态的平衡是稳定平衡。
干扰力
P ≥ Pcr
P = Pcr
干扰力
干扰力
干扰力去掉后，杆件不能回到直线位置， (2) P ≥ Pcr ; 干扰力去掉后，杆件不能回到直线位置，而继 续弯曲失去承载能力，称压杆直线状态的平衡是不稳定平衡 不稳定平衡。 续弯曲失去承载能力，称压杆直线状态的平衡是不稳定平衡。 干扰力去掉后， (3) P = Pcr ; 干扰力去掉后，杆件在干扰力作用下的微弯位 置保持平衡，不再回到直线位置，称压杆是随遇平衡 随遇平衡。 置保持平衡，不再回到直线位置，称压杆是随遇平衡。
40 1.5 1.5m 100 z y
【解】
Iy
I = I min = I y
100 × 403 20 i= = = mm A 12 × 100 × 40 3 µ l 0.7 ×1.5 ×103 × 3 λ= = = 90.9 i 20
λP = π
E
σP
70 ×103 =π × = 62.8 175
σP=200MPa。试求可用欧拉公式计算临界力时杆的长度。 试求可用欧拉公式计算临界力时杆的长度 试求可用欧拉公式计算临界力时杆的长度。
P 【解】 λ P = π
µl
E
σP
200 ×103 =π × = 99.3 200
A π d 2 / 4 4l = µl =l = λ= i I π d 4 / 64 d
l
l
长度系数
µ =1
µ=2
材料力学实验 压杆稳定实验

材料力学实验 压杆稳定实验

应该注意压杆的弯曲是在其弯曲刚度最小的平面内发生因此欧拉公式中的i因为截面的最小形心主惯性矩即实验测定临界载荷可将两组电阻应变片沿加工好的细长杆杆长方向两侧粘贴好并将杆置于三种不同的约束条件下两端固定两端铰支一端固定一端铰支使杆件轴向受压测试各点应变
《工程力学实验》项目五：
压杆稳定实验
哈尔滨工业大学力学实验教学中心
五、应变测量电路与测试技术
应变测量电路 应变片的电阻变化由电阻应变仪进 行测量，其测量电路是惠斯顿电桥。 • 流经电阻R1的电流为： • R1两端的电压降为： • R4两端的电压降为： • B、D端输出电压为： • 当 时，输出电压为零， 称为电桥平衡。 惠斯顿电桥
哈尔滨工业大学力学实验教学中心
几种常用的组桥方式
三、实验原理
• 对于轴向受压的理想细长杆件，按小变形理论， 其临界载荷可以按照欧拉公式计算：
2 EI Fcr ( l ) 2
• 应该注意，压杆的弯曲是在其弯曲刚度最小的平 面内发生，因此欧拉公式中的I因为截面的最小形 心主惯性矩，即
2 EI min Fcr ( l ) 2
• 实验测定临界载荷，可将两组电阻应变片沿加工好的细长 杆杆长方向两侧粘贴好，并将杆置于三种不同的约束条件 下（两端固定、两端铰支、一端固定一端铰支），使杆件 轴向受压，测试各点应变。绘制应力——应变曲线，做应 力——应变曲线的水平渐近线就得到临界载荷Fcr。
1.单臂测量 • 若R1为测量片，则输出桥压为：
2.半桥测量 • 若R1和R2为测量片，则输出桥压为：
3.全桥测量 • 若四个应变片同时接入测量电桥，则电桥的输出电压为：
哈尔滨工业大学力学实验教学中心
温度补偿
• 若测试过程中环境温度变化明显,则对 测试结果影响很大。因为:1.温度变化 将引起应变片电阻值改变;2.温度变化 时,由于应变片敏感栅与被测构件材料 线膨胀系数不同而将产生附加应变。 为此应采取温度补偿措施。 • 若R1为测量片,则R2与R1相同的应变片, 并把它粘贴在与被测构件相同的材料 上,放在与R1相同的环境中,但不受载 荷。 • 应变片R2称之为温度补偿片。必须注 意,工作片和温度补偿片的电阻值、灵 敏系数以及电阻温度系数应相同。
材料力学 压杆稳定

材料力学 压杆稳定

y F
l
F
x
O h b
(a )
l1
F
F
x
z
(b )
§5
实际压杆的稳定因数
st

cr cr
ncr cr


§6
压杆的稳定计算.压杆的合理截面

F
F A
A
§5
实际压杆的稳定因数
st

cr cr
ncr cr
然后根据微弯的屈曲平衡构形，由平衡条件和 小挠度微分方程以及端部约束条件，确定不同刚性 支承条件下弹性压杆的临界力。
压杆的平衡构形、平衡路径及其分叉
FP FP
Δ
压杆从直线平衡构 形到弯曲平衡构形的 转变过程，称为“屈 曲”。由于屈曲，压 杆产生的侧向位移， 称为屈曲位移。
FP FP
FP FP FP


§6
压杆的稳定计算.压杆的合理截面
F 源自F AA影响压杆承载能力的因素:
1. 细长杆
Fcr
EI
2
L 2
影响因素较多,与弹性模量E，截 面形状，几何尺寸以及约束条件 等因素有关。
2. 中长杆
Fcr cr A a b A
L
利用欧拉公式计算前面钢板尺的临界应力
EI
2
Fcr
L
2

EI
2
L
2
I max
1 32 12
3
mm
4
I min
32 1 12
3
mm
4
210 10
2 3
32 1 12

材料力学第十二章压杆的稳定


Pcr
=
π 2 EI (µL)2
= π 2EI
L2e
- - - - Euler formula
where : Le = µ L - - effective length;
µ - - coefficient of length concerned with boundary conditions
12-2 Limitation of the Euler Formulas and Slenderness
3. Stability
n=Pcr/Pmax=406/42=9.7 >nallow=8
Being in stable
12-3 提高压杆稳定性的措施
●尽量减小压杆长度 对于细长杆,其临界载荷与杆长平方成反比。因此,减小杆长可以显著
地提高压杆承载能力。在某些情况下,通过改变结构或增加支点可以达到 减小杆长、提高压杆承载能力的目的。例如,图a、b所示的两种桁架,不难 分析,两种桁架中的杆①、④均为压杆,但图b中的压杆承载能力要远远高 于图a中的压干杆。
Find the shortest length L for a steel
column with pinned ends having a cross-sectional area of 60
by 100 mm, for which the elastic Euler formula applies. Let
●合理选用材料
在其它条件均相同的情形下,选用弹性模量E数值大的材料,可以提高大 柔度压杆的承载能力,例如钢杆临界载荷大于铜、铸铁或铝制压杆的临界 载荷。但是,普通碳素钢、合金钢以及高强度钢的弹性模量数值相差不 大。因此,对于细长杆,若选用高强度钢对压杆临界载荷影响甚微,意义不大, 反而造成材料的浪费。但对于粗短杆或中长杆,其临界载荷与材料的比例 极限σP,和屈服强度σYP有关,这时选用高强度钢会使临界载荷有所提高。

第三部分材料力学选择题教程

第三部分材料力学选择题第一章绪论1．构件的强度、刚度和稳定性_______。

A、只与材料的力学性质有关；B、只与构件的形状尺寸有关；C、与上述二者都有关；D、与上述二者都无关。

2．均匀性假设认为，材料内部各点的___________是相同的。

A、应力；B、应变；C、位移；D、力学性质。

3．根据小变形条件可以认为_______。

A、构件不变形；B、构件不破坏；C、构件仅发生弹性变形；D、构件的变形远小于其原始尺寸。

4．外力包括_______。

A、集中载荷和分布载荷；B、静载荷和动载荷；C、所有作用在物体外部的力；D、载荷和支反力。

5．在下列说法中，_______是正确的。

A、内力随外力的增大而增大；B、内力与外力无关；；C、内力的单位是N或kN ；D、内力沿杆轴是不变的。

6．静定杆件的内力与其所在截面的_______可能有关。

A、形状；B、大小；C、材料；D、位置。

7．在下列关于内力与应力的讨论中，说法_______ 是正确的。

A、内力是应力的代数和；B、内力是应力的矢量和；C、应力是内力的平均值；D、应力是内力的分布集度。

8．在杆件的某斜截面上，各点的正应力_______。

A、大小一定相等，方向一定平行；B、大小不一定相等，但方向—定平行；C、大小不一定相等，方向也不一定乎行；D、大小一定相等，但方向不—定平行。

9．在杆件的某一横截面上，各点的剪应力_______。

A、大小一定相等；B、方向一定平行；C、均作用在同—平面内；D、—定为零。

10．在一截面上的任意点处，正应力σ与剪应力τ的夹角a为_______。

A、90°；B、45°；C、0°；D、任意角。

11．应力的量纲是_______。

A、ML-1T-2；B、MLT-2；C、ML2T-2；D、ML3T-2。

12．在轴向拉压杆和受扭圆轴的横截面上分别产生 _______。

A、线位移、线位移；B、角位移、角位移；C、线位移、角位移；D、角位移、线位移。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Fcr上
2 EI
(2 xl )
2

2 EI
(l 2 x)
2
Fcr中
w
l x 4
Fcr
(0.5l ) 2
l/ 4
x
2 EI
B
l/ 2
A、B两点为反弯点，其弯矩为零。 AB段相当于两端简支的情况，上下两端相当于一 端固定，一端自由的情况。
l
A
l/ 4
x
y
材料力学
第12章 压杆稳定
cr
RA
l
Fcr 2 EIw M ( x ) F w F ( l x ) 令： k cr RA y EI m FRA 2 F w k w (l x ) 其通解为： EI FRA w (0) w ( l ) 0 w A sin kx B cos kx (l x) 边界条件： Fcr w(0) (0) 0 FRA 1 w [ sin kx l cos kx (l x)] FRAl Fcr k 1 、w(0) 0 B Fcr 2 最小非零解 FRA EI 2、w(0) (0) 0 A Fcr kFcr (0.7l )2 kl 4.49
A为压杆中点的挠度，可以是任意的微小值。 采用近似挠曲线。
材料力学
第12章 压杆稳定
§12-2 细长压杆临界压力 二、一端固定，一端铰支的压杆 x 图示压杆在临界压力作用下，在xy面内处于微 F 弯平衡，试求临界荷载。 A EIw M ( x) F 解： 挠曲线近似微分方程 B端存在约束反力偶，故A端存在支反力。 w 弯矩方程 M ( x) Fcr w FRA (l x)

Fcr
A
两端固定
0.5
l
A
l
B
B
材料力学
第12章 压杆稳定
Fcr
h
§12-2 细长压杆临界压力
EI Fcr ( l )2 1、在哪一个平面内失稳？
b
y z
x
y
六、讨论
2
x
x
杆端约束在各方向上相同，在最小的刚度平面内失稳。 Fcr A 两个平面内失稳的临界压力中取小值。 A 2、在哪一个杆段失稳？
§12-2 细长压杆临界压力 五、欧拉公式统一式 l：压杆的计算长度（自由长度、相当长度） 2 EI Fcr l：压杆的实际长度 ( l )2 ：长度因数（长度系数） ，与杆端约束情况有关。
Fcr A
Fcr A
两端铰支
B
1 0.7 2
l
l
B
一端固定一端铰支
Fcr
一端固定一端自由
cr
w
B y
w
Fcr M (x )
EIw M ( x) Fcr w
w k 2 w 0
Fcr 令：k EI
2
l
二阶常系数微分方程
x
y
其通解为： w A sin kx B cos kx
0 sin kl 1 0 kl n cos kl
边界条件： w(0) w(l ) 0
cr
A
w
B
w
Fcr M (x )
x
n2 π 2 EI Fcr (n 0,1, 2,......) 2 l 理论上只有n=0的解不符合，取其最小解
当n = 1 时： F cr
x
l
l
y
y
2 EI
l2 瑞士科学家欧拉1774年提出，通常称为欧拉公式。
挠曲线方程
w A sin
半波正炫曲线
§12-3 欧拉公式适用范围、临界应力总图 一、压杆的临界应力
临界应力：压杆在临界荷载作用下，直线平衡时， 横截面上的正应力。
F cr = cr A
2 EI Fcr ( l ) 2
I i A
2
2E cr l 2
( i )
令
l
i
2E cr 2
材料力学
第12章 压杆稳定
FN ≤[ st ] A nst
§12-4 压杆的稳定计算 一、压杆稳定的条件
[ st ]

[ st ] 稳定许用应力
1、由临界应力计算 nst 2、由强度许用应力计算 [ st ] [ ]
（）
cr

稳定安全系数 nst＞1 折减系数（稳定因素）
B
B cr
3、w(l ) 0 tan kl kl
x
材料力学
第12章 压杆稳定
x Fcr
§12-2 细长压杆临界压力 三、一端自由，一端固定 其临界压力同样可根据用挠曲线方程求出。 但根据其变形形态，也可用类比法得到： 2 EI
Fcr (2l ) 2
l
y
l
四、两端固定
Fcr
l-2x
FN 270 103 53.68MPa 4 A 2 25.15 10 ≤[ st ](1 5%) 55.5MPa
3、强度校核 削弱截面需进行强度校核
FN ≤[ ] Aj FN 270 103 Aj 2 25.15 104 4 0.01 0.03
两个平面内同时失稳
h y yc
两端约束在各个方向相同 则应使得I y I z 单个槽钢 A0 25.15cm2，I z 0 934.5cm4，I y 0 83.4cm4
z0 1.75cm，t 1cm
t
h 2 I y 2[ I y 0 A0 ( z0 ) ] I z 2I z 0 2、稳定校核 i 2 I z 0 934.5 61mm 2 2 A0 25.15 h 2 F I y 0 A0 ( z0 ) I z 0 N ≤[ st ] [ ] l 1.3 7 149 2 A i 0.061 h 2 83.4 25.15(1.75 ) 934.5 Q235钢，b类截面，查表可得： 2
材料力学
第12章 压杆稳定
§12-3 欧拉公式适用范围、临界应力总图 三、临界应力总图
σcr
σu A
B
σcr =a-bλ
σcr =
C
π 2E r
σp
O
λ2
σcr = π E λ2
2
D
小柔 λu 中柔 λp 大柔 度杆 度杆 度杆
λ = ul i
cr与的关系图线 u （ cr s） cr a b （u p） 2E （≥ p） 2 AB段，小柔度杆，短而粗，因强度而破坏. BC段，中柔度杆，因失稳而破坏，但不能 应用欧拉公式. CD段，大柔度杆，细而长，因失稳而破坏.
材料力学
第12章 压杆稳定
第十二章 压杆稳定
材料力学
第12章 压杆稳定
• • • • •
本部分主要内容 压杆稳定的概念 细长压杆的临界力 欧拉公式的适用范围及经验公式 提高压杆稳定性的措施
材料力学
第12章 压杆稳定
§12-1 压杆稳定的概念
一、工程实例
①强度 构件的承载能力： ②刚度 ③稳定性
工程中有些构

l
i
，
为一无量纲的参数，称为压杆的长细比（柔度），
综合反映了压杆的①截面几何形状和尺寸②杆端约束③压杆 的实际长度对临界荷载的影响。 适用条件 临界应力 cr ≤ P比例极限 二、欧拉公式的适用范围 欧拉公式的推导采用了近 2E 2E P 似挠曲线微分方程，压杆失 cr = 2 ≤ P ≥ P 稳时仍处于弹性范围内。 P : 应用欧拉公式的压杆柔度的界限值.
件具有足够的强度、 刚度，却不一定能 安全可靠地工作。
材料力学
第12章 压杆稳定
§12-1 压杆稳定的概念
一、工程实例
压杆失稳造成的灾难 1907年8月9日,在加拿大离魁北克城14.4km横跨圣劳伦斯 河的大铁桥在施工中倒塌.灾变发生在当日收工前15分钟,桥上 74人坠河遇难.原因是在施工中悬臂桁架西侧的下弦杆有二节失 稳所致. 1909年汉堡一60万m3储气罐由于支撑结构失稳而破坏。 杭州某研发生产中心的厂房屋顶为园弧形大面积结构,屋面 采用预应力密肋网架结构,密肋大梁横截面(600mm×1400mm), 屋面采用现浇板,板厚120mm .2003年2月18日晚19时,当施工到 26～28轴时,支模架失稳坍塌,造成重大伤亡事故。 美国哈特福特城的体育馆网架结构，平面92m×110m,突然 于1978年破坏而落地，破坏起因可能是压杆屈曲。以及1988年 加拿大一停车场的屋盖结构塌落，1985年土耳其某体育场看台 屋盖塌落，这两次事故都和没有设置适当的支撑有关。
不同的材料，ψ值可查工程手册。 ＜1 稳定条件满足，则强度条件也满足. 二、压杆稳定计算 1、稳定安全系数法 FN ≤[ st ] cr
A nst
2、折减系数法 注意：

FN ≤[ st ] [ ] A
①当压杆横截面局部有削弱时，稳定计算采用毛面积， 但削弱截面强度校核时，采用净面积。 ②折减系数法设计截面时， ψ或λ与截面的形状和尺寸 有关，需采用试算的方法设计。
l
Fcr
C 不同杆段失稳的临界压力中取小值。 3、弹性支承 B B 会定性分析，约束越强，临界压力越大。 0.7＜＜2 4、安全因素 欧拉公式理想力学模型：均质直杆，轴向压力 工程实际的压杆往往存在①初曲率②材质不均匀③荷载偏心 等不利的因素，可在安全系中考虑。
l2
l1
材料力学
第12章 压杆稳定
h 8.14cm
0.311
材料力学
第12章 压杆稳定
例题1 厂房钢柱长7m，由两根16号槽钢组成，两端用螺栓借助连接板 与基础、梁连接，同一截面最多有四个螺栓孔，长度因素 1.3， 钢柱承受的压力位270kN,[ ]=170MPa，