当前位置：文档之家 › 欧拉公式的适用范围与经验公式.

欧拉公式的适用范围与经验公式.

  • 格式：ppt
  • 大小：336.00 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

2.5.2细长压杆临界力计算—欧拉公式讲解

2.5.2细长压杆临界力计算—欧拉公式讲解
2 2 3
1 6 10 120 110 200 i 4
l
三、欧拉公式的适用范围
E E cr 2 p 2 P
2 2
p
的压杆为细长压杆（或大柔度杆件）。
小结：
稳定性的概念：压杆稳定是指平衡状态的稳定性。
欧拉公式：
EI Pcr 2 l
2
E cr
2
2
欧拉公式的适用范围：大柔度杆件或细长杆件。
LOGO
51.26kN

Pcr
2 EI
2l
2 200103 2.6 106
2
2 5000
2
z
86 102
各种支承约束条件下等截面细长压杆临界力的欧拉公式 支承情况
两端铰支 一端固定 两端固定 另端铰支 一端固定 另端自由 Pcr 两端固定但可沿 横向相对移动 Pcr
2
Pcr
2 EI
(2l )
2
Pcr
2 EI
l2
=1
0.7
=0.5
=2
=1
0.5l
二、临界应力
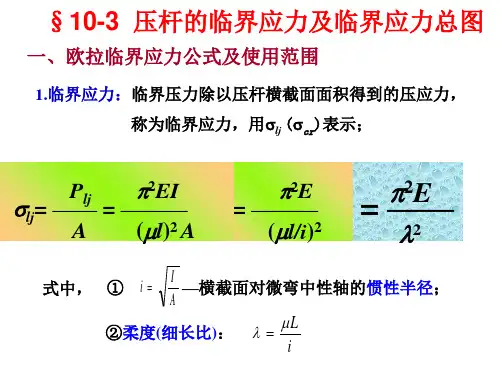
在临界力的作用下，细长压杆横截面上的平均应力叫做压杆的临界应力。
Pcr 2 EI cr A l 2 A
令
I 2 i A
则
i
I A
式中
i — 回转半径（惯性半径） ，单位mm。
工程力学应用
细长压杆的临界力公式—欧拉公式
一、临界力
压杆的临界力大小可以由实验测试或理论推导得到。
临界力的大小与压杆的长度、截面形状及尺寸、材料以及
两端的支承情况有关。
两端铰支的细长压杆临界力计算公式：

经验公式和临界应力总图

经验公式和临界应力总图

欧拉公式的适用范围经验公式一、临界应力A l EI A F σ22cr cr )(πμ==I i A=令 ， i ：惯性半径 令 ，λ：压杆的柔度（长细比）。

i lμλ=()(/)22222ππE E i l l i μμ=⋅=22πE λ=二、 欧拉公式的适用范围或 =≤2cr p 2πE σσλ=1pπE σλ≥2p πE σλ令 λ ≥ λ1的杆称为大柔度压杆或细长压杆。

当 λ＜λ1 但大于某一数值 λ2的压杆不能应用欧拉公式，此时需用经验公式。

Q235钢，取 E =206GPa ，σp =200MPa ，得916p 20610ππ10020010E σλ⨯==≈⨯三. 常用的经验公式式中：a 和b 是与材料有关的常数，可查表。

直线公式 s cr σλ≤-=b a σ 的杆为中柔度杆，其临界应力用经验公式计算。

12λλλ<≤或 ba s σλ-≥ba s σλ-=2令1λλ≥12λλλ<≤四、压杆的分类及临界应力总图1.压杆的分类2cr 2πE σλ=λb a σ-=cr scr σσ=（1）大柔度杆 （2）中柔度杆 （3）小柔度杆 2λλ≤2.临界应力总图 s cr σσ=λb a σ-=cr 22cr πλE σ=crσλλ1 λ2 p σsσ例题压杆截面如图所示。

两端为柱形铰链约束，若绕y 轴失稳可视为两端固定，若绕z轴失稳可视为两端铰支。

杆长l=1m，材料的弹性模量E=200GPa，p=200MPa。

求压杆的临界应力。

30mm yz解： ==1p π99E σλ31(0.030.02)120.0058m 0.030.02y y I i A=⨯==⨯30mm y z m 0087.0==AI i z z15.0==z y μμ11586====z z z y y y i l i lμλμλλz > λy ，所以压杆绕 z 轴先失稳， 且 λz =115 > λ1，用欧拉公式计算临界力。

小柔度杆9-4欧拉公式的应用范围经验公式

小柔度杆9-4欧拉公式的应用范围经验公式
16
§9-4 欧拉公式的应用范围经验公式
四、压杆的分类及临界应力总图
1.压杆的分类 （1）大柔度杆
1
π 2 EI Fcr ( l )2
（2）中柔度杆
2 1
σcr a b σcr σs
17
（3）小柔度杆
2
§9-4 欧拉公式的应用范围经验公式
x x
y
y z
880 1000
880
z
8
§9-3 其它支座条件下细长压杆的临界压力
x x F
880 1000
880
l
y
y z
z
F
分析思路： （1）杆件在两个方向的约束情况不同；
（2）计算出两个临界压力. 最后取小的一个作为压杆
的临界压力.
9
§9-3 其它支座条件下细长压杆的临界压力
x
π 2 EI 3.142 2.1 1011 6.5 10 8 Fcr 2 ( l ) (1 1)2 134.6kN
15
§9-4 欧拉公式的应用范围经验公式
三. 常用的经验公式
直线公式 或 令
σcr a b s
a s b a s 2 b
式中：a 和 b是与材料有关的常数，可查表得出.
2 是对应 直线公式的最低线.
2 1的杆为中柔度杆，其临界应力用经验公式.
第九章 压 杆 稳 定
1
§9-3 其它支座条件下细长压杆的临界压力
2
§9-3 其它支座条件下细长压杆的临界压力
1.细长压杆的形式
两 端 铰 支 一端 自由 一端 固定
两 端 固 定
一端 固定 一端 铰支

第九章压杆稳定(3)

第九章压杆稳定(3)

u 进行稳定性计算时，可忽略若压杆的局部削弱，仍用原来 截面的面积和惯性矩计算临界应力；
u 进行强度计算时，应按削弱后的面积计算。
11
《材料力学》国家精品课
§9. 5 压杆的稳定校核
工作安全系数 稳定安全系数
n Fcr F
nst
稳定计算 满足稳定性要求时，应有:
n
Fcr F
nst
稳定安全系数与强度安全系数的取值
《材料力学》国家精品课
1
《材料力学》国家精品课
§9. 4 欧拉公式的适用范围 经验公式
1 临界应力 临界压力
临界应力
Fcr

2EI ( l)2
cr

Fcr A
2EI ( l)2 A
将惯性矩写为
I i2A
i 惯性半径
cr

2Ei2 A ( l)2 A
2E l 2
求： 活塞杆直径d 。 F
解： 这是截面设计问题。
活塞杆所受压力
F 1 D2 p 3980 N
4
临界压力的最大值为 Fcr nst F 23900 N
先假设为大柔度杆 用欧拉公式计算临界压力
23
《材料力学》国家精品课
F
活塞杆所受压力 临界压力的最大值为 先假设为大柔度杆
直线经验公式 cr a b
5
《材料力学》国家精品课
3 直线经验公式
当 cr p 时，欧拉公式不成立。工程上使用经验公式。
直线经验公式
cr a b
式中, a, b是与材料有关的常数(表9.2)。
材料
a(MPa) b(MPa)
Q235钢 s=235MPa 优质碳钢s=306MPa

欧拉公式的适用范围经验公式

欧拉公式的适用范围经验公式

解：在正视图平面内弯 曲时，截面将绕z轴转动，
A、B二处视为铰支约束；
bh3 μ = 1, Iz = 12 ,iz =
Iz A
=
h 23
λz
=
μl iz
= 132.6
在俯视图平面内弯曲时，截面将绕y轴转动，A、
B二处视为固定端约束；
μ
=
0.5, I y
=
b3h 12
,iy
=
Iy A
=
b 23
λy
=
欧拉公式的适用范围 及经验公式
当轴向压力F 等于临界压力Fcr时，压杆才可能 由直线平衡过渡到微弯状态保持平衡。
临界压力的双重性： 1、细长压杆保持直线平衡的最大载荷； 2、细长压杆保持微弯平衡的最小载荷。
细长压杆的临界压力（欧拉公式）
π 2 EI Fcr = (μl)2
注意：欧拉公式是在线弹性的条件下建立，只有材料 服从胡克定律，即杆内的应力不超过材料的比例极限， 才能用欧拉公式计算压杆的临界压力。
μl iy
= 99.5
由于 z>y 压杆将在正视图平面内失稳。
且有： λz = 132.6 > λp = 100
故，根据欧拉公式计算临界应力
cr
2E 2
2 205109
132.62
115.07MPa
临界载荷为
Fcr cr A cr (bh)
115.07 106 40 60 106 276.17kN
σcr
=
π2E λ2
σp
或者
λ
π2E σp
=
λp
p—仅与材料的弹性模量 E 及比例极限p有关。 即： ≥p 时，欧拉公式才成立。压杆称为大柔度杆。

欧拉公式的适用范围与经验公式

欧拉公式的适用范围与经验公式
该图为Q235钢压 杆的临界应力总图。 图中，抛物线和欧拉 曲线在C处光滑连接， C点对应的柔度C=123， 临界应力为134MPa。 由于经验公式更符合 压杆的实际情况，故 在实用中，对Q235钢 制成的压杆，当 C=123 时才按欧拉公 式计算 临界应力，当 ＜123时，采用抛物线公式计算临界应力。
1) 判断压杆的失稳平面。如果压杆在各个纵向平面内的杆端约 束情况相同，则弯曲刚度最小的形心主惯性平面为失稳平面；如果 压杆在各个纵向平面内的弯曲刚度相同，则杆端约束弱的纵向平面 为失稳平面；如果压杆在各个纵向平面内的杆端约束和弯曲刚度均 各不相同，则在两个形心主惯性平面中柔度较大的为失稳平面。
2) 根据柔度值，采用相应公式计算临界力和临界应力。如果是 大柔度压杆，采用欧拉公式计算；如果是中、小柔度压杆，则根据 经验公式计算。
压杆在xz平面内，杆端约束为两端固定，μ=0.5。惯性半径为
iz
b 50103 m 14.43103 m
12
12
柔度为
y
l
iy
0.5 2 14.43103
69.3
目录
压杆稳定\欧拉公式的适用范围与经验公式 由于z>y，故压杆将在xy平面内失稳。 2）计算压杆的临界力。因 z=86.6< C=123 ，故采用抛物线公
目录
力学
式计算压杆的临界应力：
cr=235 0.00668 2=185 MPa
压杆的临界力为
Fcr=cr A=185106Pa8010－35010－3m2=740103 N=740 kN
目录
压杆稳定\欧拉公式的适用范围与经验公式
1.3 临界力和临界应力的计算步骤
由例9.1～例9.3，可得出压杆的临界力和临界应力的计算步骤 如下：

7-3压杆稳定计算-精选文档

7-3压杆稳定计算-精选文档

5m
7m
9m
d
2 2 9 E ( 200 × 10 ) = = 99 . 35 6 p= 200 × 10 P
c > p
属于大柔度杆 （a） （b） (c)
故用欧拉公式计算临界压力
2 EI Fcr 3136 KN 2 = ( l )
例2 ：1000吨双动薄板液压冲压机的顶出器杆
σ σ
∴ σcr ≤σp
2E 有 p = p
或
E p
2
3、对λ<λp的压杆，不能用欧拉公 式，可用后面介绍的经验公式.
第三节
欧拉公式的适用范围
经验公式
三、经验公式 （1） 三类不同的压杆
细长杆（大柔度杆）—发生弹性屈曲,失稳 λ> λp 中长杆（中柔度杆）—发生弹塑性屈曲，失稳 λs < λ <λp 或 σp < σcr < σs
例1:三根直径均为d=16cm的圆杆，其长度及支承情况如图示。圆杆材料为
Q235钢，E=200GPa,σp=200MPa，试求： 1.哪一根压杆易丧失稳定？ 2.三杆中最大的临界压力值。
解： 压杆的柔度越大，临界压力 越小，越容易失稳。 1.计算柔度
4 I d × 4 d i= = 2 = A 64 × d 4 l 1 5 杆a: 1 2 5 2 i 4 1 0 l 0 . 7 7 杆b: 1 2 2 . 5 2 i 4 1 0 l 0 . 5 9 杆c: 1 1 2 . 5 2 i 4 1 0
粗短杆（小柔度杆）—不发生屈曲，而发生屈服 λ <λs 或
σs < σcr
第四节
压杆的稳定性计算

压杆的临界应力

压杆的临界应力
§10-3 压杆的临界应力及临界应力总图
一、欧拉临界应力公式及使用范围
1.临界应力：临界压力除以压杆横截面面积得到的压应力， 称为临界应力，用slj (scr)表示；
s = —— slj=
—P—lj
=
p2EI
———
A (l)2 A
p2E slj= ———
(l/i)2
lj
p2E
l2
式中， ① i I —横截面对微弯中性轴的惯性半径； A
例4：图示结构，CF为铸铁圆杆，直径
d1=10cm，[s]=120MPa , E=120GPa。 BE为A3钢圆杆, 直径d2=5cm，
[s]=160MPa, E=200GPa, 如横梁视为刚
性，a＝2m，求许可荷载F。
A
解：1、结构为一次超静定求杆内力
MA 0:
2FNB4FNC6F0
E F
D BC
lp
p2200109
200106
100
用柔度表示的临界压力：
p 2E Fcr l2 • A
l≥lp——细长杆(大柔度杆)，
当压杆的长细比λ＜λp时，欧拉公式已不适用。在工程 上，一般采用经验公式。在我国的设计手册和规范中给
出的是直线公式和抛物线公式。
二、中柔度杆临界应力的经验公式
1.ss>scr>sp时采用经验公式：
①直线公式：
scrabl
1)∵scr<ss，∴
ss abl
，得到：l0
a
ss
b
2) lp≥l≥l0—中粗杆(中柔度杆)；
3)对于A3钢： l0a bss 31 0. 12 4240 60
4）对于式中的系数a,b，下表给出了一些常用材料的数值。

工程力学第3节 欧拉公式及经验公式

工程力学第3节 欧拉公式及经验公式
一、临界应力与压杆柔度 压杆处于临界状态时，将压杆的临界载荷除以横 截面面积 A，得到横截面上的应力，称为压杆的临界 应力，用 cr 表示。由公式知：
Fcr 2 EI cr A ( l ) 2 A
令
i
I A
2 2 2 Ei E cr 2 l 2 ( l ) ( )
cr a1 b12
2 cr 2E
P

例11-5 3 根材料相同的圆形截面压杆，均为一端固 定、一端自由，如图所示，直径均为 d 100mm，皆 P 200 MPa， 由 Q235 钢制成，材料的 E 206 GPa， a 304 MPa， S 235 MPa， b 1.12 MPa。试求各杆 的临界载荷。
cr a b S
a S S b
注意：仅当压杆的柔度 S时，才能用上式求解！ 例：对于 Q235 钢： S 235MPa ，a 304 MPa ，
b 1.12 MPa
a S 304 235 63 S 1.12 b
综述 （1）
对于由合金钢、铝合金、铸铁等制作的 压杆，根据其柔度可将压杆分为三类：
P 的压杆，称为大柔度杆或细长杆
由欧拉公式 计算其临界应力 （2）S
cr 2E p
2
P 的压杆，称为中柔度杆或中长杆
由直线型经验公 式计算临界应力
cr a b
中柔度杆的 在 60 ~ 100 之间。实验指出，这种压 杆的破坏性质接近于大柔度杆，也有较明显的失稳 现象。
三、经验公式 若压杆的柔度 P，则这种压杆的临界力不能再 按欧拉公式计算。对于此类压杆，工程中通常采用 以实验结果为依据的经验公式来计算其临界应力。 1、直线型经验公式

3压杆稳定计算

3压杆稳定计算
mm, E=2.0×105 MPa, p=200 MPa, s=240 MPa,
nw=2.5。求容许轴向压力F。
Fx
A
l
B
y
解： (1) 计算压杆的柔度，判明欧拉公式是否可用
惯性半径
I π (D4 - d 4 )/64 A π (D4 - d 4 )/4
i I/A
查得一端固定一端铰支压杆的长度系数为
二、欧拉公式的适用范围 σ cr =
2E
λ2
1、小变形（挠曲线微分方程） 2、公式推导中，用到了中性层的曲率公 式，而曲率公式导出时用到了胡克定律， 因此，欧拉公式适用于胡克定律的适用范 围内：比例极限内。
∴ σcr ≤σp
说明: 1、σ cr ≤σp的杆件叫细长杆，或大 柔度杆。
2、当σcr =σp
I π (D4 - d 4 )/64 4.6010-6 m4
故有临界力
Fcr＝π(2lE)I2 7.41 105 N
而容许轴向压力为
F Fcr 296 kN
nw
此种直接根据稳定安全因数对压杆稳定计算的方法称为稳定安全因数法。
例4：木柱，b=12cm, h=20cm, l=7 m,λp=110, E=10GPa,由A、B两销子固定。 试
求:Fcr
z
y b
F
h
A
B
Fx
解：
l
（1）若在xoz平面内失稳，绕y轴转动

1,
Iy

bh3 12
8000
cm4 , l

7m

y

l
iy


l
/
Iy A
121 p

《材料力学 第2版》_顾晓勤第08章第3节 欧拉公式及经验公式

《材料力学 第2版》_顾晓勤第08章第3节 欧拉公式及经验公式

cr a1 b12
cr
2E 2
P
第 3 节 欧拉公式及经验公式
第八章 压杆稳定
例8-5 3 根材料相同的圆形截面压杆，均为一端固
定、一端自由，如图所示，直径均为 d 100mm，皆 由 Q235 钢制成，材料的 E 206 GPa， b 200 MPa， S 235 MPa，a 304 MPa，b 1.12 MPa。试求各杆
Fcr2 cr2 A 214106 0.00785N 1680 kN
（c）第三根压杆的临界载荷
3
l3
i
2 0.5 0.025
40
P 60
该杆为小柔度压杆，临界应力应选取屈服极限：
cr3 S 235 MPa Fcr3 =cr3 A 235106 0.00785N 1845 kN
的临界载荷。
解：3 根杆相同的参数
P
E
P
100
2m 1m 0.5m
S
a S
b
61.6
A d 2
4
=0.00785 m2
(a)
(b)
(c)
第 3 节 欧拉公式及经验公式
第八章 压杆稳定
i
I A
d 4
0.025 m
2
（a）第一根压杆的临界载荷
1
l1
i
22 0.025
160
P 100
cr1
第 3 节 欧拉公式及经验公式
第八章杆处于临界状态时，将压杆的临界载荷除以横
截面面积 A，得到横截面上的应力，称为压杆的临界
应力，用 cr 表示。由公式知：
cr
Fcr A
2EI (l)2 A
令 i I A
令 l

压杆稳定的概念两端铰支细长杆的临界压力其

压杆稳定的概念两端铰支细长杆的临界压力其

2
若杆端在各个方向的约束情况不同（柱形绞），应分别 计算杆在不同方向失稳时的临界力。I 为其相应的对 中性轴的惯性矩。
例9-3-1： 图示各杆材料和截面均相同，试问哪一根杆能承受 的压力最大， 哪一根的最小？
a
P
(1)
P
1.3a
(2)
P
(3)
1.6a
因为
又
可知
（1）杆承受的压力最小，最先失稳； （3）杆承受的压力最大，最稳定。
F
a
A
B
a\2
c
解：
故取
例9-3-2：已知：图示压杆EI,且杆在B支承处不能转动
求：临界压力
例9-3-3：由A3钢加工成的工字型截面杆，两端为柱形绞。在xy平面内失稳时，杆端约束情况接近于两端绞支，z = 1，长度为 l1 。在xz平面内失稳时，杆端约束情况接近于两端固定 y = 0.6 ，长度为 l2 。求 Fcr。
压杆任一 x 截面沿 y 方向的 位移为 y = f (x)
该截面的弯矩为
m
m
y
B
y
x
其中 I 为压杆横截面的 最小形心主惯性矩。 令 则有二阶常系数线性微分方程 m m y B y x
其通解为
01
A，B，k 三个待定常数由该挠 曲线的三个边界条件确定。
02
边界条件：
得
B=0
B=0 ，
1 的大小取决于压杆的力学性能。例如，对于Q235钢，可取 E=206MPa，P=200MPa，得
右图称为欧拉临界应力曲线。实线部分是欧拉公式适用范围的曲线，虚线部分无意义。
o
经验公式
二、压杆的临界应力总图
解：
圆形截面杆：

压杆稳定(II)-水电类

压杆稳定(II)-水电类

三类不同压杆的失效形式
细长杆 (λ ≥ λp) — 发生弹性失稳 中长杆 (λo≤ λ < λp) — 发生弹塑性失稳 屈曲） （屈曲） 短粗杆 短粗杆(λ < λo) — 发生强度破坏
a −σs ∴ λo = b 判断压杆类型， ⑵ 判断压杆类型，并计算临界应力
λ ≥ λp： 细长杆 λo≤ λ < λp ： 中长杆 λ < λ o：
I d i= = A 4
5m
9m
d
(a) (b)
1×5 20 = λa = = ia d d 4
µl
0.5×9 18 λb = = = ib d d 4
µl
λa ＞ λb
∴
Fcr(a) < Fcr (b)
例题
F F
d
已知丝杠： 已知丝杠： d=40 mm, l=375 mm, 45号钢 45号 F＝80 kN, nw=4.0 求： 校核丝杠的 丝杠的稳定性 校核丝杠的稳定性
8 ϕ = 0.867 + (0.863 − 0.867 ) = 0.864 10
从而得稳定许用应力：
[σ cr ]= ϕ [σ ] = 0.864 × 170 MPa = 146.9 MPa
而连杆横截面上的工作应力为
F 70 × 10 3 N σ = = = 126 .8 MPa p φ [σ ] −6 2 A 552 × 10 m
例题11例题 -5 机械中的工字形截面连杆，两端为柱形铰，从而 该连杆如在xy平面内失稳，可取长度因数µz=1.0；如在xz平面内 失稳，则可取µy=0.5。已知：连杆由Q235钢锻造成型，它属于a 类截面中心压杆。该连杆承受的最大轴向压力为F = 70kN，材 料的强度许用应力[σ ]=170 MPa。试校核其稳定性。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
若令 λ p π E/σp ，则上述适用范围又可写成
E λ λ p σp
三、经验公式
(9-6)
欧拉公式只适用于 p 的大柔度杆，对于 λ ＜ λ p
的非细长压杆一般采用经验公式。
(1)合金钢、铝合金、铸铁和木材
cr a b
a s s b
(9-7)
(9-8)
Fp A z F p′
y
h
解 压杆AB左右两端 为圆柱销联接，它与球 铰约束不同。在主视图
b
a)
B
h
Fp
F p′
l
b)
平面内弯曲时，两端可
b
以自由转动，相当于铰
链；而在俯视图平面内 弯曲时，两端不能转动
图9-6
近似视为固定端。因为压杆是矩形横截面，故在主视图平
面内失稳时，截面将绕轴z 转动；而在俯视图平面内失稳 时，截面将绕轴y 转动。因此，应先计算压杆在两个平面 内的柔度，以确定在哪一个平面内失稳。在主视图平面 内，取长度系数 z 1，压杆柔 度为
cr a1 b12
式中，a1和b1均为与材料力学性能有关的常数。
பைடு நூலகம்
例9-1 由Q235钢制成的矩形截面杆，其受力和两端约 束情况如图9-6所示，图a为主视图，图b为俯视图。在杆 的两端A、B处为圆柱销联接。已知l=2300mm，b=40mm，h=
60mm，材料的弹性模量E=205GPa，试求此杆的临界载苛。
μyl 0.5 2300 λ 99.6 y iy 11.55
因λ y ，故压杆首先在主视图平面内失稳，且在此平 z ＞λ 面内λ p =100为细长杆，故临界载荷为 z ＞λ
π2E 2 205103 40 60 Fcr σcrA 2 bh N 2 λ 132.8
Iz bh3 / 12 3h 3 60 iz mm 17.32mm A bh 6 6 μzl 1 2300 λ 132.8 z iz 17.32
同理
3b 3 40 iy mm 11.55mm 6 6
在俯视图平面内，取长度系数 y 0.5 ，压杆柔度为
cr
cr s
A
如图(9-4)
cr a b
B
s p
2E cr 2
C
1)对于 ＜ s 的小柔度
杆，失效时没有失稳现象， 按压缩强度问题处理；

O
s
p
图9-4
2)对于 ≥ p 的大柔
度杆采用欧拉公式(9-5)计算；
3)对于 s ≤ ＜ p 的中 柔度杆， 用直线经验公式(9-7)
第三节 欧拉公式的适用范围与经验公式
一、临界应力 Fcr 2EL cr A ( μl ) 2 A 式中，A为压杆的横截面面积。 令
(9-3a)
i 2 L/A
Fcr 2EL 2E cr 2 A (μl ) A (μl ) 2 i
(9-3b)
式中， i 为横截面的惯性半径，于是式(9-3a)可以改成
引用无量纲记号
λμl /i
(9-4)
代入式(9-3b)得
2E cr 2
式中， 称为柔度或长细比。
二、欧拉公式的适用范围
(9-5)
压杆的临界应力在不超过材料的比例极限бp时，欧拉 公式(9-2)或式(9-5)才可应用，也就是欧拉公式的适用范围 为
2E E σcr 2 σp或 σp
275.3 103 N
275.3 kN
计算临界应力。 (2)结构钢及低合金结构钢(如图9-5所示)
cr
对于 p的大柔度杆，
2E cr 2
s
采用欧拉公式(9-2)计算临 界应力；对于0＜ ＜ p 的 小柔度杆和中柔 度杆，按
O
小柔度杆
中柔度杆
大柔度杆
抛物线公式计算临界应力，
图9-5
cr
即
(9-9)