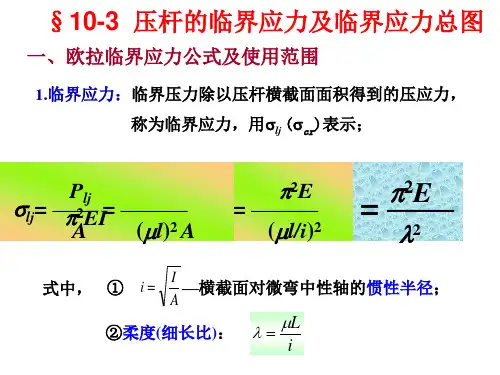
欧拉公式的适用范围
经验公式
一、临界应力
A l EI A F σ22cr cr )(πμ==I i A
=令 ， i ：惯性半径 令 ，λ：压杆的柔度（长细比）。 i l
μλ=()(/)22222ππE E i l l i μμ=?=22πE λ
=
二、 欧拉公式的适用范围
或 =≤2
cr p 2πE σσλ=1p
πE σλ≥2p πE σλ令 λ ≥ λ1的杆称为大柔度压杆或细长压杆。
当 λ＜λ1 但大于某一数值 λ2的压杆不能
应用欧拉公式，此时需用经验公式。 Q235钢，取 E =206GPa ，σp =200MPa ，得
9
16p 20610ππ10020010
E σλ?==≈?
三. 常用的经验公式
式中：a 和b 是与材料有关的常数，可查表。 直线公式 s cr σλ≤-=b a σ 的杆为中柔度杆，其临界应力用
经验公式计算。
12λλλ<≤或 b
a s σλ-≥b
a s σλ-=2令
1λλ≥12λλλ<≤四、压杆的分类及临界应力总图
1.压杆的分类
2
cr 2
πE σλ=λ
b a σ-=cr s
cr σσ=（1）大柔度杆 （2）中柔度杆 （3）小柔度杆 2λλ≤
2.临界应力总图 s cr σσ=λb a σ-=cr 2
2
cr πλE σ=cr
σλ
λ1 λ2 p σs
σ
例题压杆截面如图所示。两端为柱形铰链约束，若绕
y 轴失稳可视为两端固定，若绕z轴失稳可视为两端铰支。杆长l=1m，材料的弹性模量E=200GPa，
p
=200MPa。
求压杆的临界应力。
30mm y
z
解： ==1p π99E σλ31(0.030.02)120.0058m 0.030.02y y I i A
=?=
=?30mm y z m 0087.0==A
I i z z
1
5.0==z y μμ11586====z z z y y y i l i l
μλμλλz > λy ，所以压杆绕 z 轴先失稳， 且 λz =115 > λ1，用欧拉公式计算临界力。 kN
5.89π2
2
cr cr =?==z E A A σF λ30mm
y z 欧拉公式的适用范围·经验公式
例题：外径 D = 50 mm ，内径 d = 40 mm 的钢管，两端 铰支，承受轴向压力F 。材料为 Q235钢，E = 200 GPa ， σp = 200 MPa ， σs = 240 MPa ，a =304MPa ，b =1.12MPa 。 求：（1）能用欧拉公式时压杆的最小长度；（2）当压 杆长度为上述最小长度的3/4 时，压杆的临界应力。 解：1. 能用欧拉公式时压杆的最小柔度 ==1p
π100E σλ
2
222444
14)(π64)(πd D d D d D A I i +=--==1004122=≥+==
λμμλd D l i l 2222
1min 1000.050.04= 1.6m 441
D d l l λμ++≥==?压杆 μ = 1，
2. 用直线公式计算
m 2.14
3min ==l l 122754λμμλ<=+==d
D l i l λλ<=-=-=5712
.1240304s 2b σa kN 5.155)(4
π)(22cr cr =--=?=d D b a σA F λ
本讲结束