第12章单因素方差分析
- 格式:doc
- 大小:1.16 MB
- 文档页数:8




12章多元线性表12-9两个模型的方差分析表
ANOVA'模型
方差分析(ANOVA)又称“变异数分析”或“F检验”,是R。
A.Fister发明的,用于两个及两个以上样本均数差别的显著性检验。
由于各种因素的影响,研究所得的数据呈现波动状。
造成波动的原因可分成两类:一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素。
方差分析的定义:
方差分析就是通过检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。
方差分析的基本思想
通过分析研究中不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小。
从形式上看,方差分析是比较多个总体的均值是否相等,但本质上它所研究的是变量之间的关系。
在研究一个或者多个分类型自变量与一个数值型因变量之间的关系时,方差分析是其中的主要方法之一。
这与回归分析方法有很多相同之处,但是又有本质区别。
方差分析不仅可以提高检验的效率,同时由于它将所有的样本信息结合在一起,因此增加了分析的可靠性。
一般来说,随着增加个体显著性检验的次数,偶然因素导致差别的可能性也会增加。
方差分析方法则是同时考虑所有的样本,因此排除了错误积累的概率,从而避免拒绝了一个真实的原假设。

重复测量设计资料的ANOV A重复测量的定义重复测量(repeated measure)是指对同一研究对象的某一观察指标在不同场合(occasion,如时间点)进行的多次测量,用于分析该观察指标在不同时间点上的变化规律。
例如,为研究某种药物对哮喘病病人的治疗效果,需要定时多次测定受试者的FEV1,以分析其的变动情况。
再如,药效研究中要观察给药后不同时间点上的血药浓度。
重复测量设计的优缺点•优点:每一个体作为自身的对照,克服了个体间的变异。
分析时可更好地集中于处理效应.因重复测量设计的每一个体作为自身的对照,所以研究所需的个体相对较少,因此更加经济。
•缺点:滞留效应(Carry-over effect)前面的处理效应有可能滞留到下一次的处理.潜隐效应(Latent effect)前面的处理效应有可能激活原本以前不活跃的效应.学习效应(Learning effect)由于逐步熟悉实验,研究对象的反应能力有可能逐步得到了提高。
第一节重复测量资料ANOV A对协方差阵的要求重复测量资料方差分析的条件:1. 正态性处理因素的各处理水平的样本个体之间是相(个体内不独立)互独立的随机样本,其总体均数服从正态分布;2. 方差齐性相互比较的各处理水平的总体方差相等;3. 各时间点组成的协方差阵(covariance matrix)具有球对称(sphericity)特征。
若球形性质得不到满足,用随机区组设计方差分析的F值是有偏的,这会造成I型错误增加。
一般ANOV A 的协方差矩阵22211121222212222221222111121212211212222()(1)()()(1)a aa a aa i i i i i i i ijij ii jjs s s s s s V s s s s y y n s y y y y n y y y y n sr s s⎛⎫ ⎪ ⎪=⎪ ⎪ ⎪⎝⎭=--=---=-=∑∑∑∑∑L L M M M M L 211222222114000000aa aa s s V s s s ⎛⎫ ⎪⎪=⎪⎪ ⎪⎝⎭==LL M M M M L L对于第章,几个处理组间的协方差矩阵为:且假定重复测量资料的协方差矩阵时间点间的协方差矩阵实验前 5周后 10周后 实验前 0.081 0.090 0.065 5周后 0.386 0.411 10周后0.723时间点间的相关系数实验前 5周后 10周后 实验前 1 0.507 0.269 5周后 1 0.777 10周后122211121222212222221222111121212211212222()(1)()()(1)a aa a aa i i i i i i i ijij ii jjs s s s s s V s s s s y y n s y y y y n y y y y n sr s s⎛⎫ ⎪ ⎪=⎪ ⎪ ⎪⎝⎭=--=---=-=∑∑∑∑∑L L M M M M L球形对称的实际意义22211121222212222221222111121212211212222()(1)()()(1)a a a a aa i i i i i i i ijij ii jjs s s s s s V s s s s y y n s y y y y n y y y y n s r s s⎛⎫ ⎪ ⎪=⎪ ⎪ ⎪⎝⎭=--=---=-=∑∑∑∑∑L L M M M M L 所有两两时间点变量间差值对应的方差相等对于y i 与y j 两时间点变量间差值对应的方差可采用协方差矩阵计算为:122222222211221222i ji j i jy y y y y y y y ss s ss s s s--=+-=+-如:球形对称的实际意义举例122222222211221222i ji j i jy y y y y y y y ss s ss s s s--=+-=+-如:协方差阵A 1A 2A 3A 4A 11051015A 25201520A 310153025A 415202540s 1-22 = 10 + 20 -2(5) = 20s 1-32 = 10 + 30 -2(10) = 20s 1-42 = 10 + 40 -2(15) = 20s 2-32 = 20 + 30 -2(15) = 20s 2-42 = 20 + 40 -2(20) = 20s 3-42 = 30 + 40 -2(25) = 20本例差值对应的方差精确相等,说明球形对称。

单因素方差分析1. 引言•单因素方差分析(One-way ANOVA)是一种常用的统计方法,用于比较两个或多个组之间的均值是否存在显著差异。
•在实际研究中,我们经常需要比较不同组之间某个变量的均值差异,例如不同教育水平对收入的影响,不同药物对疾病的治疗效果等。
•单因素方差分析提供了一种统计方法,可以判断不同组之间均值差异是否由随机因素引起,还是由于真正的因素差异引起。
2. 基本概念•因素(Factor):需要比较不同组之间的变量,也称为自变量或分类因素。
•水平(Level):每个因素具有的不同取值或组别,也称为处理或条件。
•观测值(Observation):每个组内的单个实验结果或数据点。
•总平均(Grand Mean):所有组的观测值的平均值。
•组内平均(Group Mean):每个组的观测值的平均值。
•组间平均(Between-group Mean):所有组的观测值的平均值。
3. 假设检验•零假设(H0):不同组的均值之间没有显著差异。
•备择假设(H1):不同组的均值之间存在显著差异。
4. 单因素方差分析的步骤1.收集数据:按照分类因素进行分组,获得每个组的观测值。
2.计算总平均:计算所有观测值的平均值。
3.计算组内平均:计算每个组的观测值的平均值。
4.计算组间平均:计算所有组的观测值的平均值。
5.构造统计模型:建立协方差矩阵和方差矩阵之间的关系。
6.计算平方和:计算组内平方和和组间平方和。
7.计算均方差:计算组内均方差和组间均方差。
8.计算F值:计算F统计量,用于检验组间均值差异是否显著。
9.假设检验:比较F值与临界值,确定是否拒绝零假设。
5. F分布与p值•在单因素方差分析中,我们使用F分布来进行假设检验。
•F分布是一种连续概率分布,取值范围大于等于0,且分布形状根据自由度的不同而变化。
•在单因素方差分析中,我们计算出的F值可以与F分布表中的临界值进行比较,以确定是否拒绝零假设。
•p值是统计假设检验中的一个重要指标,表示在零假设成立的情况下,观察到的样本数据或更极端结果出现的概率。
第12章方差分析(Analysis of V ariance)方差分析是鉴别各因素效应的一种有效统计方法,它是通过实验观察某一种或多种因素的变化对实验结果是否带来显著影响,从而选取最优方案的一种统计方法。
在科学实验和生产实践中,影响一件事物的因素往往很多,每一个因素的改变都有可能影响产品产量和质量特征。
有的影响大些,有的影响小些。
为了使生产过程稳定,保证优质高产,就有必要找出对产品质量有显著影响的那些因素及因素所处等级。
方差分析就是处理这类问题,从中找出最佳方案。
方差分析开始于本世纪20年代。
1923年英国统计学家R.A. Fisher 首先提出这个概念,(ANOV A)。
因当时他在Rothamsted农业实验场工作,所以首先把方差分析应用于农业实验上,通过分析提高农作物产量的主要因素。
Fisher1926年在澳大利亚去世。
现在方差分析方法已广泛应用于科学实验,医学,化工,管理学等各个领域,范围广阔。
在方差分析中,把可控制的条件称为“因素”(factor),把因素变化的各个等级称为“水平”或“处理”(treatment)。
若是试验中只有一个可控因素在变化,其它可控因素不变,称之为单因素试验,否则是多因素试验。
下面分别介绍单因素和双因素试验结果的方差分析。
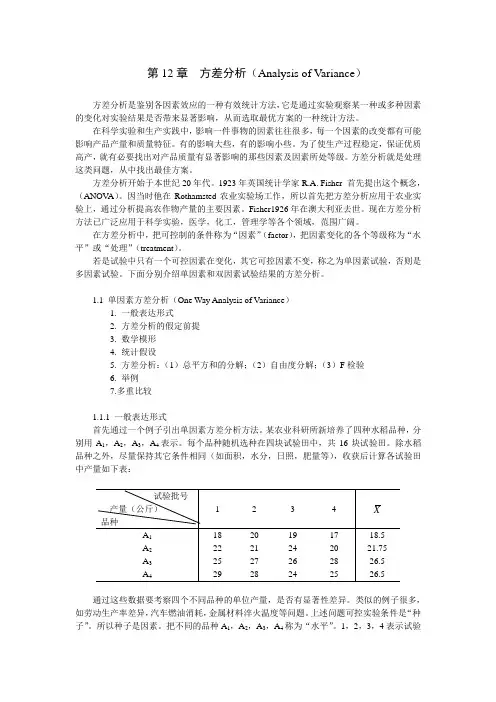
1.1 单因素方差分析(One Way Analysis of Variance)1.一般表达形式2.方差分析的假定前提3.数学模形4.统计假设5.方差分析:(1)总平方和的分解;(2)自由度分解;(3)F检验6.举例7.多重比较1.1.1 一般表达形式首先通过一个例子引出单因素方差分析方法。
某农业科研所新培养了四种水稻品种,分别用A1,A2,A3,A4表示。
每个品种随机选种在四块试验田中,共16块试验田。
除水稻品种之外,尽量保持其它条件相同(如面积,水分,日照,肥量等),收获后计算各试验田中产量如下表:通过这些数据要考察四个不同品种的单位产量,是否有显著性差异。

单因素方差分析原理
单因素方差分析是一种常用的统计方法,用于比较一个因素对于不同组之间的差异是否显著。
其基本原理是利用组内变异与组间变异之间的比较来判断因素对于不同组的影响程度。
在单因素方差分析中,我们将总体的方差分解为两个部分:组间方差和组内方差。
组间方差反映了不同组之间的差异程度,而组内方差反映了同一组内观测值之间的差异。
通过计算组间方差和组内方差的比值,可以得到F值,即F
统计量。
F统计量的大小反映了因素对于不同组之间的差异是
否显著。
如果F值显著大于1,表明组间方差较大,差异显著,因素对于不同组之间的差异有显著影响;反之,如果F值接
近1,则说明组间方差较小,差异不显著,因素对于不同组之
间的差异没有显著影响。
进行单因素方差分析时,需要满足一些基本假设,如观测值之间的独立性、组内方差的同质性等。
此外,还需要使用适当的假设检验方法和确定显著水平,以判断因素对于不同组之间的差异是否显著。
总之,单因素方差分析通过比较组内变异与组间变异,能够帮助我们判断一个因素对于不同组之间的差异是否显著,从而得出相应的结论。
这种统计方法在实验设计和数据分析中经常被应用,对于研究因素的影响具有重要的意义。

统计学(山西财经大学)知到章节测试答案智慧树2023年最新第一章测试1.职工人数是连续型变量。
参考答案:错2.总体可分为有限总体和无限总体。
参考答案:对3.利润是离散型变量。
参考答案:错4.利用图表或其他数据汇总工具分析数据属于描述统计。
参考答案:对5.研究太原市老年人的生活习性,则个体是参考答案:太原市每一位老年人6.2018年各省城镇家庭的人均收入数据属于参考答案:截面数据7.研究者想要了解的总体的某种特征值称为参考答案:参数8.一份报告称,“由150部新车组成的一个样本表明,外国新车的价格明显高于本国生产的新车”,这一结论属于参考答案:对总体的推断9.为了顾及城市拥有汽车的家庭比例,抽取500个家庭,得到拥有汽车比例为35%,则35%是参考答案:统计量的值10.下列叙述采用推断统计方法的是参考答案:从果园中采摘50个桔子,利用其平均重量估计果园中桔子的平均重量第二章测试1.二手数据的采集成本低,但搜集比较困难参考答案:错2.研究人员根据对研究对象的了解,有目的选择一些单位作为样本的调查方式是判断抽样参考答案:对3.统计调查的资料按照来源不同,分为原始资料和二手资料参考答案:对4.方便抽样是一种典型的概率抽样。
参考答案:错5.为了调查某校学生的学习积极性,从男生中抽取30人,从女生中抽取50人进行调查,这种调查方法属于参考答案:分层抽样6.下面哪种抽样调查结果不能对总体参数进行估计参考答案:判断抽样7.为了解居民对小区物业服务的意见,调查人员随即抽取了50户居民,上门进行调查。
这种搜集数据的方法属于参考答案:面访式调查8.下列陈述哪一个是错误的参考答案:非抽样误差只存在于概率抽样中9.下面哪种抽样方式属于概率抽样参考答案:系统抽样;分层抽样;整群抽样10.与概率抽样相比,非概率抽样的优点是参考答案:操作简便;对统计专业技术要求不高;时效快;成本低第三章测试1.某连续变量数列,其末组组限为 500 以上,又知其邻组组中值为480 ,则末组的组中值为参考答案:5202.在对数据分组时,若某个数据的值正好等于相邻组的下限时,一般应将其归在参考答案:下限所在组3.用组中值作为各组变量值的代表值参考答案:当变量值在本组内呈均匀分布时代表性高4.下列哪个图形保留了原始数据的信息参考答案:茎叶图5.某单位 100 名职工按工资额分为 300 以下、 300-400 、 400-600 、 600-800 、 800 以上等五个组。
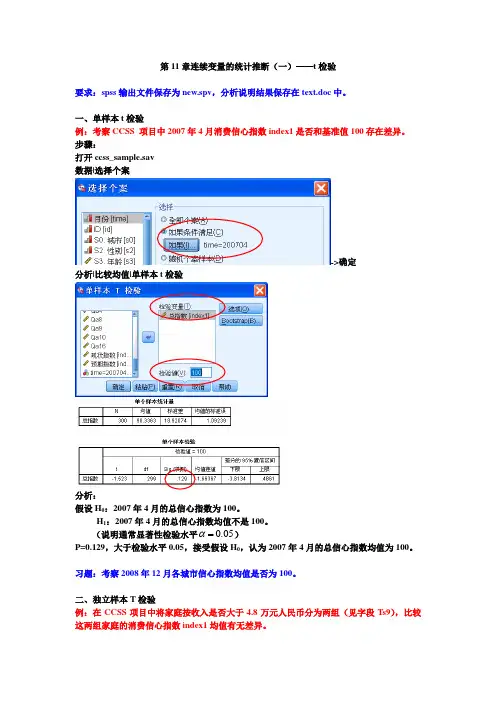
第11章连续变量的统计推断(一)——t 检验要求:spss 输出文件保存为new.spv ,分析说明结果保存在text.doc 中。
一、单样本t 检验例:考察CCSS 项目中2007年4月消费信心指数index1是否和基准值100存在差异。
步骤:打开ccss_sample.sav 数据|选择个案->确定分析|比较均值|单样本t 检验分析:假设H 0:2007年4月的总信心指数为100。
H 1:2007年4月的总信心指数均值不是100。
(说明通常显著性检验水平05.0=α)P=0.129,大于检验水平0.05,接受假设H 0,认为2007年4月的总信心指数均值为100。
习题:考察2008年12月各城市信心指数均值是否为100。
二、独立样本T 检验例:在CCSS 项目中将家庭按收入是否大于4.8万元人民币分为两组(见字段Ts9),比较这两组家庭的消费信心指数index1均值有无差异。
步骤:说明:由于上题选择部分记录,而本题对所有记录分析,所以先要选择全部记录。
数据|选择个案|全部个案|确定分析|均值检验|独立样本T检验分析:Levene方差齐性检验,p=0.027,小于0.05,认为两个样本所在总体的方差不齐。
假设H0:两个家庭收入级别在总指数上没有差异。
H1:两个家庭收入级别在总指数上有差别。
选用假设方差不相等的t检验结果,p=0.000,小于0.05,拒绝H0,认为两个家庭收入级别在总指数上有差异。
习题:在CCSS项目中,以2007年4月的数据为例,分析不同家庭收入等级(Ts9)的信心指数index1均值有无差异。
三、配对设计样本均数的比较例:用某药治疗10名高血压病人,对每一个病人治疗前后的舒张压(mmHg)进行了测试,问该药有无降压作用。
数据ptest1.sav步骤:2、配对t检验分析|均值比较|配对样本T检验分析:假设H0:同一病人治疗前后的舒张压没有差异。
H1:同一病人治疗前后的舒张压有差异。

方差分析方差分析是对多个总体均值是否相等这一假设进行检验。
下面通过一个例子说明方差分析的内容。
例:某化妆品生产公司研制出一种饮料。
饮料的颜色共有四种,分别为橘黄色、粉色、绿色和无色透明。
随机从五家专卖市场上收集了前一期该种饮料的销售量,如表9-1所示。
这是一个方差分析问题,即对四种不同颜色的饮料的销售量均值是否相等进行检验。
我们把四种不同颜色的饮料的销售量均值分别记为,由题意知,要检验假设;不全相等如果检验结果为不全相等,则表明饮料颜色对销售量产生影响。
反之,如果检验结果为不存在显著影响,则可以认为饮料颜色对销售量没有影响,他们来自于相同的总体。
方差分析的基本概念在方差分析中,常常用到一些术语。
我们把要考察的对象的某种特征称为指标。
试验条件分为可控制的和不可控制的两类,称可控制的试验条件为因素;因素所处的状态称为该因素的水平。
如果在一项试验中只有一个因素在变化,称他为单因素试验。
若试验中变化因素多于一个,称他为双因素以及多因素试验。
在上例中,饮料的销售量为指标,饮料的颜色为因素,饮料的四种颜色为该因素的四个水平,该例是一个单因素四水平试验。
上一章所讲的对两个总体均值的比较,实际上就是单因素两水平试验。
下面,我们简单阐述单因素方差分析的基本原理。
1.2单因素方差分析1.2.1 单因素方差分析的基本原理单因素方差分析是研究一个因素的变化对试验指标的影响是否显著的统计分析方法,是方差分析中最简单的情形。
设因素A有r个水平在水平下进行次独立试验,试验记录如表9-2其中表示第i水平进行第j次试验的可能结果。
假设,。
待检假设为:,不全相等。
如果成立,那么r个总体间无显著差异,即是说因素A对试验结果的影响不显著,所有可视为来自同一个总体,各间的差异只是由随机因素引起的。
若不成立,则在所有的总变差中,除随机波动引起的变差外,还应包括由于因素A的不同水平作用产生的差异。
如果不同水平作用产生的差异比随机因素引起的差异大得多,就认为因素A 对试验结果有显著影响,否则就认为因素A对试验的影响不显著。
第12章方差分析(Analysis of V ariance)方差分析是鉴别各因素效应的一种有效统计方法,它是通过实验观察某一种或多种因素的变化对实验结果是否带来显著影响,从而选取最优方案的一种统计方法。
在科学实验和生产实践中,影响一件事物的因素往往很多,每一个因素的改变都有可能影响产品产量和质量特征。
有的影响大些,有的影响小些。
为了使生产过程稳定,保证优质高产,就有必要找出对产品质量有显著影响的那些因素及因素所处等级。
方差分析就是处理这类问题,从中找出最佳方案。
方差分析开始于本世纪20年代。
1923年英国统计学家R.A. Fisher 首先提出这个概念,(ANOV A)。
因当时他在Rothamsted农业实验场工作,所以首先把方差分析应用于农业实验上,通过分析提高农作物产量的主要因素。
Fisher1926年在澳大利亚去世。
现在方差分析方法已广泛应用于科学实验,医学,化工,管理学等各个领域,范围广阔。
在方差分析中,把可控制的条件称为“因素”(factor),把因素变化的各个等级称为“水平”或“处理”(treatment)。
若是试验中只有一个可控因素在变化,其它可控因素不变,称之为单因素试验,否则是多因素试验。
下面分别介绍单因素和双因素试验结果的方差分析。
1.1 单因素方差分析(One Way Analysis of Variance)1.一般表达形式2.方差分析的假定前提3.数学模形4.统计假设5.方差分析:(1)总平方和的分解;(2)自由度分解;(3)F检验6.举例7.多重比较1.1.1 一般表达形式首先通过一个例子引出单因素方差分析方法。
某农业科研所新培养了四种水稻品种,分别用A1,A2,A3,A4表示。
每个品种随机选种在四块试验田中,共16块试验田。
除水稻品种之外,尽量保持其它条件相同(如面积,水分,日照,肥量等),收获后计算各试验田中产量如下表:通过这些数据要考察四个不同品种的单位产量,是否有显著性差异。
类似的例子很多,如劳动生产率差异,汽车燃油消耗,金属材料淬火温度等问题。
上述问题可控实验条件是“种子”。
所以种子是因素。
把不同的品种A1,A2,A3,A4称为“水平”。
1,2,3,4表示试验批号,即每次随机的选取某个地块种某个品种的种子。
称此种问题为单因素试验。
单因素试验通常分多个试验批号,目的是平衡一些不可控因素带来的影响。
如土地的基本条件不一样。
如各品种只试验一次,必然在试验结果中含有不可控因素带来的影响。
在众多的数据中,怎样判别不同品种的水稻产量是否存在显著性差异?初步观察A 1品种的产量可能低一些,A 3,A 4的产量可能高一些。
这是从平均数上观察。
若按前面介绍的两个总体的比较,需要作C 24= 6次检验。
比较麻烦,所以需要方差分析方法。
首先从数学上给出这类问题的一般形式(单因素)这表明该可控因素共有k 个水平,每个水平都进行m 次试验,某个水平上的m 次试验可当作一个样本看待。
X i j 表示第i 个水平上第j 次试验的结果。
很容易看出当水平只有2个时,这相当于两个总体的均值的显著性检验问题。
现在的目的是要分析各个水平上的均值是否有显著性差异。
1.1.2 方差分析的假定前题 (1)每个水平(A i )上的随机变量X i 的分布都是正态的,即服从N(μi , σ2)。
但μi ,(i = 1, …, m ),σ2未知。
每个水平上的一系列观测值,看作是取自该水平正态总体的一个容量为m 的样本。
(2)认为k 个水平上的k 个总体方差相等,都是σ2(方差齐性)。
(3)观测值X i j 相互独立。
这三个假定在实际中一般都能得到满足。
1.1.3 数学模型因为X i j ~ N (μi , σ2),(i = 1, …, k )所以可以把观测值X i j 分解为两部分,即X i j = μi + e i j , (i = 1, …, k ),(j = 1, 2, …, m )其中e i j 表示X i j 对μi 的随机偏差。
为便于比较水平不同对X i j 造成的影响,可以把μi 也分解成两部分μi = μ + αi (i = 1, …, k )其中μ = ∑=ki i k 11μ,称为总平均(Grand mean ),αi 称为A i 水平上的效应,它满足∑αi = 0 把μi 代入上式则有:X i j = μ + αi + e i j , ∑αi = 0, (i =1, 2, …, k ),(j =1, 2, …, m )e i j 表示随机变量,αi 表示水平变量。
这就是单因素方差分析的数学模型。
1.1.4 统计假设:若可控因素的不同水平对试验结果无显著性影响,那么观测值X i j 应该来自同一正态总体,X i j ~ N(μ, σ2)。
所以对应的零假设是H 0:μ1 = …, μi ….= μk = μ 或 α1 =, …, = αk = 0 H 1:μi 不全相等或αi 不全为零。
当H 0成立时,样本的行平均数i X 必然差异不大,差异表现为随机误差,当H 1为真时,i X 间必存在较大差异,这时差异表现为系统误差。
1.1.5 方差分析方法为判别不同水平对试验结果有无显著性影响,关键是把观测值变量中的随机误差和系统误差分开,并能进行比较,问题就解决了。
(1) 分解总离差平方和(Total Sum of Squares ),S T =∑∑==-ki mj ij X X 112)(方法是在S T 公式中加入行平均数i X 。
S T =∑∑==-ki mj ij X X 112)(=∑∑==-+-ki mj i i ij X X X X 112)]()[(=∑∑==-k i m j i ij X X 112)(+∑∑==-k i m j i X X 112)(+∑∑==--k i mj i i ij X X X X 11))((2因为 ∑∑==--K i m j i i ij X 11))((= ∑∑==--k i mj i ij i X X X X 11)]()[(= 0所以S T =∑∑==-Ki mj ij X X 112)(=∑∑∑∑====-+-Ki mj ki mj i i ij X X X X 111122)()(令S E =∑∑-2)(i ij X XS A =∑∑==-ki mj i X X 112)(=∑=-ki i X X m 12)(则S T = S E + S A ,其中S T 称总离差平方和,总变差。
S E 称样本组内离差平方和。
它测量同一水平上因重复实验而产生的误差。
这是由于不可控因素引起的,故S E 反映的是随机误差。
S A 称样本组间离差平方和。
它表示各个水平上的样本平均数i X 与样本总平均数X 之间离差的加权平方和。
可见不同水平上的样本差异越大,S A 的值就越大。
它反映的是系统误差。
(2).求各离差平方和S T ,S A ,S E 的自由度(Degrees of freedom ),f T ,f A ,f E 。
S T =∑∑==-Ki mj ij X X 112)(的自由度。
因随机变量X ij 的个数是N 个,相互独立,但受一个约束条件。
∑∑===m i nj ij X NX 111约束,所以自由度为 N – 1,即f T = N – 1。
S A =∑∑==-ki mj i X X 112)(=∑=-ki i X X m 12)(的自由度。
因i X 的个数是k 个,但受条件∑==Ki i X m NX 11约束,所以自由度为f A = k -1。
S E =∑∑==-Ki mj i ij X X 112)(的自由度。
因X ij 的个数为N ,但受条件i X =∑=mj ij X 1,(i = 1, …, k )约束,所以自由度为f E = N – k 。
三个自由度之间也有这样的关系。
f T = f A + f E , N – 1=(N – k )+(k – 1)(3)F 检验在H 0成立条件下,X ij 服从正态分布N (μ, σ 2),又知X ij 相互独立,所以有2σTS =2112)(σ∑∑==-K i mj ij X X ~ χ2(N – 1)2σAS =2112)(σ∑∑==-K i mj i X X ~ χ2(k – 1)2σES =2112)(σ∑∑==-Ki mj i ij X X ~ χ2(N –k )且S A , S E 相互独立(证明从略)。
由抽样分布一章知,若x ~ χ2(n 1),y ~ χ2(n 2), 且x 与y 相互独立,则F =21//n y n x ~),(21n n F 当已知S A ,S E 相互独立且分别服从(k – 1)和(N – k )个自由度的χ2分布时,则有F =)()1(22k N S k S EA--σσ=)/()1/(k N S k S E A --~ F [(k –1) , ( N – k )]有了统计量F 就可以做假设检验。
怎样制定判别规则?分析如下:在H 0成立条件下,有E(1-k S A ) = E(1)(2--∑∑k X X i ) = E(1)(12--∑=k X X m ki i )= m E(1)(12--∑=k X X ki i ) = m Var )(i X = mm2σ= σ 2E(k N S E -) = E(k km S E -) = E[]1)(12--∑∑m X X k i j i =∑∑==--ki mj i ij m X X E k 1121)([1]= ∑=k i k 121σ= σ 2可见1-k S A 和kN S E -都是σ2的无偏估计量。
所以在H 0成立条件下,F =)/()1/(k N S k S E A --应接近1。
当F 值很大时,说明组间均方误差,大于组内均方误差,则不能认为k 个总体服从同一个正态分布,即拒绝H 0,否则接受H 0。
这是一个单端检验问题。
临界值由检验水平α 确定。
P{F > F α,(k – 1)(N - k )} = α 检验步骤是:(1)建立假设H :μ1 = μ2 = … = μk = μ(2)选统计量F ,H 0成立条件下F ~ F (k – 1),(N – k ) (3)由α 计算临界值F α(k – 1,N- k )(4)判别规则:若F *≤ F α(k – 1,N – k )接受H 0 若F * > F α(k – 1,N – k )拒绝H 0(5)由样本计算F *值,按判别规则给出检验结果。
通常使用方差分析表来完成F 检验。
用Eviews进行方差分析案例1 国家统计局城市社会经济调查总队1996年在辽宁、河北、山西3省的城市中分别调查了5个样本地区,得城镇居民人均年消费额(人民币元)数据如下表。