当前位置：文档之家 › 第八章 单因素方差分析(1)

第八章 单因素方差分析(1)

  • 格式：ppt
  • 大小：625.50 KB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

One-Way_ANOVA单因素方差分析_图文

One-Way_ANOVA单因素方差分析_图文

固定效应模型
xij i ij i 1, 2, , a j 1, 2, , n
其中αi是处理平均数与总平均数的离差，因这些离 差的正负值相抵，因此

i 1
n
i
0
如果不存在处理效应，各αi都应当等于0，否则至 少有一个αi≠0。因此，零假设为： H 0 ： α1＝ α2＝ … ＝ αa＝ 0 备择假设为： HA：αi ≠ 0（至少有一个i）
65.8
326.5 65.3
63.9
322.0 64.4
68.5
336.5 67.3
71.0
354.0 70.8
67.5
343.0 68.6
•因变量(响应变量):连续型的数值变量株高 •因素(Factor)：影响因变量变化的客观条件 •一个因素：“品系” 单因素方差分析 •水平(Level)：因素的不同等级 不同“处理” •五个水平：品系I-V •重复(Repeat)：在特定因素水平下的独立试验 •五次重复
第八章 单因素方差分析
Chapter 8: One-factor Analysis of Variance
方差分析：从总体上判断多组数据平均数 （K≥3） 之间的差异是否显著
方差分析将全部数据看成是一个整体，分析构成 变量的变异原因，进而计算不同变异来源的总体 方差的估值。然后进行F测验，判断各样本的总 体平均数是否有显著差异。若差异显著，再对平 均数进行两两之间的比较。
i 1 j 1 i 1 j 1
a
n
2
x
i 1 j 1
a
n
ij
xi xi x xi x xij xi 0

生物统计-8第八章单因素方差分析

生物统计-8第八章单因素方差分析

01
确定因子和水平
确定要分析的因子（独立变量） 和因子水平（因子的不同类别或 条件）。
建立模型
02
03
模型假设
根据因子和水平，建立方差分析 模型。模型通常包括组间差异和 组内误差两部分。
确保满足方差分析的假设条件， 包括独立性、正态性和同方差性。
方差分析的统计检验
01
F检验
进行F检验，以评估组间差异是否 显著。F检验的结果将决定是否拒
生物统计-8第八章单因素方差分析
目录
• 引言 • 方差分析的原理 • 单因素方差分析的步骤 • 单因素方差分析的应用 • 单因素方差分析的局限性 • 单因素方差分析的软件实现
01
引言
目的和背景
目的
单因素方差分析是用来比较一个分类变量与一个连续变量的关系的统计分析方法。通过此分析，我们可以确定分 类变量对连续变量的影响是否显著。
VS
多元性
单因素方差分析适用于单一因素引起的变 异，如果存在多个因素引起的变异，单因 素方差分析可能无法准确反映实际情况。 此时需要考虑使用其他统计方法，如多元 方差分析或协方差分析等。
06
单因素方差分析的软件 实现
使用Excel进行单因素方差分析
打开Excel，输入数据。
点击“确定”，即可得到单因素方差分析 的结果。
输出结果，并进行解释和 解读。
谢谢观看
背景
在生物学、医学、农业等领域，经常需要研究一个分类变量对一个或多个连续变量的影响。例如，研究不同品种 的玉米对产量的影响，或者不同治疗方式对疾病治愈率的影响。
方差分析的定义
定义
方差分析（ANOVA）是一种统计技术，用于比较两个或更多组数据的平均值 是否存在显著差异。在单因素方差分析中，我们只有一个分类变量。

数理统计14(方差分析)

数理统计14(方差分析)
组间变异 组内变异
总变异
统计量
其中
称为组间均方 (mean square between groups) 或因素均方 (mean square factor),
MSE

SSE nk
称为组内均方 (mean square within groups)
或误差均方 (mean square error),
第一节 单因素方差分析
一、方差分析的原理和方法
效应 (effect): 在试验中的试验结果。 因素 (factor): 影响试验结果的条件。 水平 (lever): 因素所处的不同状态或内部分类。 方差分析的目的：是探讨不同因素、不同水平
之间效应的差异，从而考察各因素对试 验结果是否有显著影响。
试验中只有一个因素取不同的水平进行试 验，而其他因素保持不变，这样的试验称为 单因素试验 (one factor trial), 相应的方差分 析就是单因素方差分析。
表8-5 例8-1的方差分析表
方差 离差
来源 平方和
Source 组间
(因素)
组内 (误差)
总和 (总变差)
SS 442.7
160.5 603.2
自由 度 df 4
15
19
均方
MS 110.68
10.7
F值 MSA MSE
10.34
P值 P<0.05
临界值 F
F0.05(4,15) =3.06
第二节 多重比较
温度(℃) 60 65 70 75 80 合计 86 80 83 76 96
xi j
89 83 90 81 93
91 88 94 84 95
90 84 85 82 94

第八章 单因素方差分析

第八章 单因素方差分析

V 4.2 3.2 4.8
4
5
1.0
0.8 1.5
-1.3
-1.1 -0.3
1.8
3.5 11.5
4.1
6.0 29.0
3.3
2.5 18.0 总和 57.0
xi
n
xi2
j 1 2 ij
2.25
1.93
9.00
3.4
132.25
29.43
841.00 324.00
174.46 68.06
1308.50
sx MS e n
品系号
Ⅳ
Ⅴ
Ⅲ
Ⅱ
Ⅰ
平均数
70.8
68.6
67.3
65.3
64.4
顺序号
1
2
3
4
5
df
k
R0.05
Rk
R0.01
Rk
2
2.95
1.165
4.02
1.588
3 20 4
3.10
1.225
4.22
1.667
3.18
1.256
4.33
1.710
5
3.25
1.284
4.40
1.738
5
单因素固定效应模型方差分析表
变异来源
处理间
平方和
自由度
均方
F
F MS A MS e
SSA
a-1
MSA
误差或处理内
总和
SSe
SST
na-a
na-1
MSe
4、平方和的简易计算方法
株号 1 2 3 I -0.4 0.3 -0.2
品 II

单因素方差分析步骤（1）

单因素方差分析步骤（1）

单因素方差分析步骤：对于只有一种因素影响的资料，例如本例只检测血型这一种变量是否影响肺活量。

我们先确立假设和确立检验标准H0：假设不同血型的人的肺活量是有差异的H1：假设不同血型的人的肺活量是没有差异的。

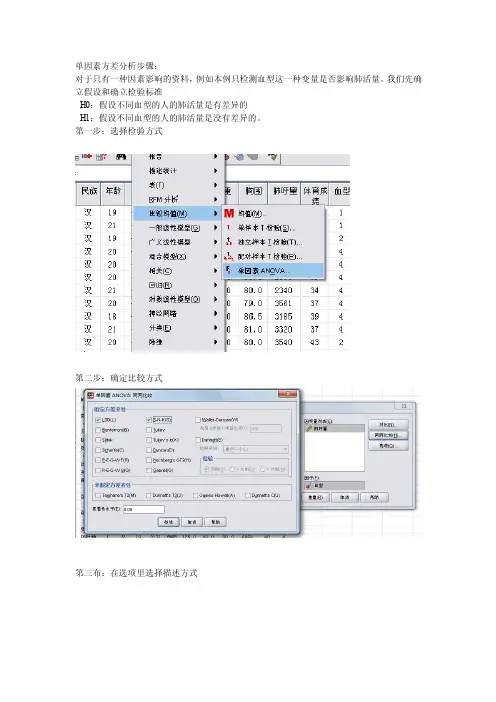
第一步：选择检验方式第二步：确定比较方式第三布：在选项里选择描述方式第四步：得出结果：由本图可知，p》0.05，可知肺活量的总体方差无差异，方差齐则可做方差分析再有下图可知：p= 0.789是大与0.05的，所以不是小概率事件，不拒绝H0，所以认为不同血型的人的肺活量是没有差异的。

随机区组设计资料的方差分析2.如果对四种饲料对猪体重增加量有无差异进行分析，则可将猪随机分组，本例中以a代表分组，b代表饲料，x代表体重增加量如图：对于这种资料分析，应选用单变量方差分析，主要是影响因素是多样的，主要描述的是体重增加量。

那么我们首先应1、确定假设：对于处理组：H0，假设三种处理方式体重增加量是相等的H1，假设三种处理方式体重增加量是不等的。

对于区组：H0，假设三组之间体重增加量是相等的H1，假设三组之间体重增加量是不等的。

2、确立检验标准a=0.053、计算统计量F F1=MS处理/MS误差F2=MS区组/MS误差4、确定p值，做出推断结论。

第一步：选择分析方式第二步：选择确立因变量，本题描述的是体重增加量，故选用x，确立区间，处理措施。

如图：第三步：确定模型，本题为确定区组a与处理措施b的交互作用，因此选用a，b交互模式。

如图：如需作图比较分组a 与处理措施b 的交互作用对体重影响有无差异可添加对比组，如图：确定观察均值的两两比较，主要针对与各分组的均值比较，及各处理方式的均值比较：在选项里设定输出，描述统计及方差齐性检验，显示分组及处理方式的均值。

最后得出结果：有本图可知F＜3，p＞0.05，可知各组间方差齐，可做方差检验。

如下图所示，可知p≥0.05，统计无差异，所以可知，三种处理方式对体重增加是无差异的。

单因素方差分析（one-wayANOVA）

单因素方差分析（one-wayANOVA）

单因素⽅差分析（one-wayANOVA）单因素⽅差分析（⼀）单因素⽅差分析概念是⽤来研究⼀个控制变量的不同⽔平是否对观测变量产⽣了显著影响。

这⾥，由于仅研究单个因素对观测变量的影响，因此称为单因素⽅差分析。

例如，分析不同施肥量是否给农作物产量带来显著影响，考察地区差异是否影响妇⼥的⽣育率，研究学历对⼯资收⼊的影响等。

这些问题都可以通过单因素⽅差分析得到答案。

（⼆）单因素⽅差分析步骤第⼀步是明确观测变量和控制变量。

例如，上述问题中的观测变量分别是农作物产量、妇⼥⽣育率、⼯资收⼊；控制变量分别为施肥量、地区、学历。

第⼆步是剖析观测变量的⽅差。

⽅差分析认为：观测变量值的变动会受控制变量和随机变量两⽅⾯的影响。

据此，单因素⽅差分析将观测变量总的离差平⽅和分解为组间离差平⽅和和组内离差平⽅和两部分，⽤数学形式表述为：SST=SSA+SSE。

第三步是通过⽐较观测变量总离差平⽅和各部分所占的⽐例，推断控制变量是否给观测变量带来了显著影响。

（三）单因素⽅差分析原理总结在观测变量总离差平⽅和中，如果组间离差平⽅和所占⽐例较⼤，则说明观测变量的变动主要是由控制变量引起的，可以主要由控制变量来解释，控制变量给观测变量带来了显著影响；反之，如果组间离差平⽅和所占⽐例⼩，则说明观测变量的变动不是主要由控制变量引起的，不可以主要由控制变量来解释，控制变量的不同⽔平没有给观测变量带来显著影响，观测变量值的变动是由随机变量因素引起的。

（四）单因素⽅差分析基本步骤1、提出原假设：H0——⽆差异；H1——有显著差异2、选择检验统计量：⽅差分析采⽤的检验统计量是F统计量，即F值检验。

3、计算检验统计量的观测值和概率P值：该步骤的⽬的就是计算检验统计量的观测值和相应的概率P值。

4、给定显著性⽔平，并作出决策（五）单因素⽅差分析的进⼀步分析在完成上述单因素⽅差分析的基本分析后，可得到关于控制变量是否对观测变量造成显著影响的结论，接下来还应做其他⼏个重要分析，主要包括⽅差齐性检验、多重⽐较检验。

应用统计学8-方差分析(1)

应用统计学8-方差分析(1)

Yi = µi + ε i
（ 8-1）
其中， μi 纯属Ai作用的结果,称为在Ai条件下Yi的真值(也称为在 Ai条件下Yi的理论平均). εi 是试验误差(也称为随机误差)。
2 ε ~ N ( 0 , σ ) 且相互独立，则 Yi ~ N ( µ i , σ 2 ) 假定 i
且也是相互独立的
第八章
第八章
方差分析
8. 2 单因素试验的方差分析
数学模型和数据结构 参数点估计 分解定理 自由度 显著性检验 多重分布与区间估计
第八章
方差分析
8. 2. 1 数学模型和数据结构
在单因素试验中,为了考察因素A的k个水平A1， A2， …， Ak对Y的影响(如k 种型号对维修时间的影响)，设想在固定的 条件Ai下作试验。所有可能的试验结果组成一个总体Yi (i=1， 2， …， k)，它是一个随机变量，可以把它分解为两部分
第八章
方差分析
8. 2. 2 参数点估计
2 , , , , µ α α α σ 估计参数 1 2 k 和
估计方法：最小二乘法
最小偏差平方和原则：使观测值与真值的偏差平方和 达到最小
第八章
偏差平方和
方差分析
8. 2. 2 参数点估计
2 S ε = ∑∑ ε ij = ∑∑ (Yij − µ i ) 2 = ∑∑ (Yij − µ − α i ) 2 i =1 j =1 k m
eij = Yij − Y i
第八章
最小二乘估计量
方差分析
8. 2. 2 参数点估计
ˆ =Y µ ˆ i = Yi − Y α µ ˆ i = Yi
可以证明，这三个估计量均为参数μ、 αi和μi的无偏估计量

第08章 单因素方差分析

第08章 单因素方差分析
=用用用i=总1SSSi=a变SSS1j=TAe表1异表a表jn=(1示平示x示(nix误j方总处i(j差和平x理xi.平x=方.平.i)误.方和)2方x2差= .和.:和)变2iS：2= ：1异iST=aS1S j平==1SjnA=[方eS1i=a=(= 1(x和xijS nin=j+j1i处(=aT Sx1xxi理i (ji..)x)变Si .(xxiij=异.a=ai=(1.S .A )11x2x平(jn=i.x.1.x)i 方(..2x.)ixx和j...(…xx.)=i.x.=.]，.)i21.i=)=a=,1a=2a)01j,n=n013xx,.i.j i=1 j=1 “.”表示对一个下标的 和
第八章 单因素方差分析
第八章 单因素方差分析
引言、单因素方差分析的概念
前面我们学习了单样本和双样本的显著性检验方法。在 科例现的假v分差检这显a8研比如验析有异ri些.然1a那活较我，为其显Rn假那检，.c么动试们我一他著某设么e验犯A，中验用们类4，性学.1每Ⅰ都个0如一称，，特A检F者对一型是品iN何对有结作s定验培接对O错独h种解一很果单情的e育V受检误立的rA决的多见因况（一了的验的的）株这情表素下1种一t概接概，，高9检类况方8的2个延率受-率也之验81问是差统小伸），（零明就间，题要分计麦。创问0假显是是.的检析共假9新造5对设增前否5个检验(需设)品出O于的加1面有小0验的检n检=种方一概。我显e0麦呢不验验，-.差个率6w们著品？止0，为分a因C都，所差种y最两5它2了析素是学正是异Aα间=好个是掌’方N1不1的确差=，是-的0样O两1握α法对同F的异做-否=V方本0样检该（0A处.检显了6有.法，。9)本新验0a。理验著55=差n就比，个平品。0a间结。异.是如l4而品均种方y0的果？s：，且与种数差iFs 今方天差所分讲析的与方t检差验分的析区。别：

最新11-第8章 单因素方差分析汇总

最新11-第8章 单因素方差分析汇总

11-第8章单因素方差分析仅供学习与交流，如有侵权请联系网站删除 谢谢140+第八章 单因素方差分析第一节 方差分析的基本问题一、方差分析要解决的问题t 检验法适用于样本平均数与总体平均数及两样本平均数间的差异显著性检验；而多个平均数间的差异显著性检验，必须用方差分析法。

1、检验过程繁琐一试验包含5个处理，采用t 检验法要进行25C 10＝次两两平均数的差异显著性检验；若有k 个处理，则要作k (k-1)/2次类似的检验。

2、无统一的试验误差，误差估计的精确性和检验的灵敏性低 12X -X s如表8-1，试验有5个处理，每个处理重复6次，共有30个观测值。

进行t 检验时，每次只能利用两个处理共12个观测值估计试验误差，误差自由度为2(6-1)=10；若利用整个试验的30个观测值估计试验误差，显然估计的精确性高，且误差自由度为5(6-1)=25。

可见在用t检法进行检验时，由于估计误差的精确性低，误差自由度小，使检验的灵敏性降低，容易掩盖差异的显著性。

3、推断的可靠性低，检验的I型错误率大用t检验法进行多个处理平均数间的差异显著性检验，由于没有考虑相互比较的两个平均数的秩次问题，因而会增大犯I型错误的概率，降低推断的可靠性。

假设每一对检验接受零假设的概率都是1-α＝0.95，而且这些检验都是相互独立的，那么10对检验都接受概率是(0.95)10＝0.60，犯错误的概率α׳=1-0.60=0.40犯I型错误的概率明显增加。

由于上述原因，多个平均数的差异显著性检验不宜用t检验，须采用方差分析法。

二、方差分析的几个概念方差分析(analysis of variance)是由英国统计学家R.A.Fisher于1923年提出的。

这种方法是将a个处理的观测值作为一个整体看待，把观测值总变异的平方和及自由度分解为相应于不同变异来源的平方和及自由度，进而获得不同变异来源总体方差估计值；通过计算这些总体方差的估计值的适当比值，就能检验各样本所属总体平均数是否相等。

最新11-第8章 单因素方差分析

最新11-第8章 单因素方差分析

11-第8章单因素方差分析仅供学习与交流，如有侵权请联系网站删除 谢谢174+第八章 单因素方差分析第一节 方差分析的基本问题一、方差分析要解决的问题t 检验法适用于样本平均数与总体平均数及两样本平均数间的差异显著性检验；而多个平均数间的差异显著性检验，必须用方差分析法。

1、检验过程繁琐一试验包含5个处理，采用t 检验法要进行25C 10＝次两两平均数的差异显著性检验；若有k 个处理，则要作k (k-1)/2次类似的检验。

2、无统一的试验误差，误差估计的精确性和检验的灵敏性低 12X -X s如表8-1，试验有5个处理，每个处理重复6次，共有30个观测值。

进行t 检验时，每次只能利用两个处理共12个观测值估计试验误差，误差自由度为2(6-1)=10；若利用整个试验的30个观测值估计试验误差，显然估计的精确性高，且误差自由度为5(6-1)=25。

可见在用t检法进行检验时，由于估计误差的精确性低，误差自由度小，使检验的灵敏性降低，容易掩盖差异的显著性。

3、推断的可靠性低，检验的I型错误率大用t检验法进行多个处理平均数间的差异显著性检验，由于没有考虑相互比较的两个平均数的秩次问题，因而会增大犯I型错误的概率，降低推断的可靠性。

假设每一对检验接受零假设的概率都是1-α＝0.95，而且这些检验都是相互独立的，那么10对检验都接受概率是(0.95)10＝0.60，犯错误的概率α׳=1-0.60=0.40犯I型错误的概率明显增加。

由于上述原因，多个平均数的差异显著性检验不宜用t检验，须采用方差分析法。

二、方差分析的几个概念方差分析(analysis of variance)是由英国统计学家R.A.Fisher于1923年提出的。

这种方法是将a个处理的观测值作为一个整体看待，把观测值总变异的平方和及自由度分解为相应于不同变异来源的平方和及自由度，进而获得不同变异来源总体方差估计值；通过计算这些总体方差的估计值的适当比值，就能检验各样本所属总体平均数是否相等。

第八讲-1 单因素方差分析

第八讲-1 单因素方差分析

1~30 甲 31~60 乙 61~90 丙 91~120 丁
4个处理组低密度脂蛋白测量值
分 组 低密度脂蛋白测量值(mmol/L) n Xi X X2
安慰剂组 3.53 4.59 4.34 2.66 … 2.59 30 3.43 102.91 367.85
降血脂新 药2.4g组 2.42 3.36 4.32 2.34 … 2.31 30 2.72 81.46 233.00
≥１
组间变异=组内变异，F=１，就没有理由拒绝H0；
组间变异＞组内变异，F＞1，F值越大，拒绝H0的理由越充分

。H0成立时，F统计量服从F分布。
F值具有组间的自由度ν1和组内的自由度 ν2。如果在给定的ν1和ν2下从正态总体中进行 一系列抽样，就可得到一系列的F值，这一
系列的F值呈F分布。
F分布曲线特征：
图 F分布曲线 （随v1和v2的不同而不同）
v1 v2
有的，将组间自由度v1称为分子的自由度 将组内自由度v2称为分母的自由度
方差分析是单侧F检验，查F临界值表，给出结论
1 组间 2 组内 F F ，P 0.05,1 , 2 0.05。
P≤0.05,拒绝H0,接受H1，样本均数不全相等; P≥0.05,不拒绝H0,不能下各样本的总体均数不全相等的结论。
3）因素的单独效应
单独效应：其他因素固定在某一水平时，因变 量在同一因素不同水平间的差别。
如性别因素固定为男，10、11岁两个年龄的差 异就是年龄因素的单独效应，得到年龄的单独 效应。
主效应：因变量在一个因素各水平间的平 均差异。
上面性别分别固定为男或女时的年龄单独效应的算 术平均值为年龄因素的主效应。
• 附表5系各种v1和v2下右尾概率α=0.05和α=0.01时的 临界F值。如查附表5，v1=3，v2=12时，F0.05 =3.49， F0.01=5.95，即表示如以v1=3（n1 =4）、v2=12（n2 =13）在一正态总体中进行连续抽样，则所得F值大 于3.49的仅有5%，而大于5.95的仅有1%。

第八章_单因素方差分析(1)

第八章_单因素方差分析(1)

a
如果我们只研究这 a个不同处理，则有
i 0,
且每个
是常数。
i
i 1
i i为第i个处理的平均数。
ij
是y
的试验的随机误差（也
ij
称为噪声）。固定效应模型
我们假定ij相互独立且服从正态分布N(0, 2)。
因此，方差分析假定yij～N( i , 2 ),这是方差分析的条件。
❖ （三）因素处理效应和实验模型的分类
因此，两两 t检验的精确性有待提高 。
正确答案：
进行关于 a(a 3)个样本平均数差异的假 设检验， 应使用一种更为合理的 统计分析方法－方差分 析。
❖ 二、方差分析的几个概念
1、方差分析（analysis of variance）：将试验数据的总变异分 解成不同来源的变异，从而评定不同来源的变异相对重要性 的一种统计方法。
2、试验指标（experiment index）：为衡量试验结果的好坏或 处理效应的高低，在试验中具体测定的性状或观测的项目。
3、试验因素（experiment factor）：试验中所研究的影响试验 指标的因素：单因素、双因素或多因素试验。
4、因素水平（level of factor）：因素的具体表现或数量等级。
答：常采用第五章里讲的t检验法。
现在，如何进行a 个样本的平均数差异的假设检验（a 3）？
某人答：两两进行t检验。
评论：这种方法是不行的。
主要原因有三：
原因（1）：检验的工作量大
当有a个样本平均数，两两组合，就有a(a 1) 个平均数的差。 2
例如，a 10时，就有109＝45个平均数的差。 2
yi•
1 n
yi•表示第i个处理所有数据的平均值

i第八章单因素方差分析

i第八章单因素方差分析

幻灯片1【例】调查了5个不同小麦品系的株高，结果如下。

试判定这5个品系的株高是不是存在显著性不同。

5个小麦品系株高(cm)调查结果幻灯片2第八章单因素方差分析One-factor analysis of variance幻灯片3本章内容第一节方差分析简述第二节固定效应模型第三节随机效应模型第四节多重比较第五节方差分析应具有的条件幻灯片4第一节方差分析简述一、方差分析的一样概念一、概念方差分析（ analysis of variance，ANOVA）：是同时判定多组数据平均数之间不同显著性的统计假设查验，是两组数据平均数不同显著性t 查验的延伸。

ANOV A 由英国统计学家R.A.Fisher首创，用于推断多个总体均数有无差异。

幻灯片5单因素方差分析（一种方式分组的方差分析）：研究对象只包括一个因素(factor)的方差分析。

单因素实验：实验只涉及一个因素，该因素有a个水平(处置)，每一个水平有n次实验重复，如此的实验称为单因素实验。

水平(level)：每一个因素不同的处置(treatment)。

幻灯片6方差分析Analysis of Variance （ANOVA )幻灯片7【例】随机选取4窝动物，每窝中均有4只幼仔，称量每只幼仔的诞生重，结果如下。

判定不同窝的动物诞生重是不是存在显著性不同。

4窝动物的诞生重 单位：g幻灯片8二、单因素方差分析的数据格式：32.9 31.4 25.7 28.0 118.0 29.50027.1 23.3 27.8 26.7 104.9 26.22533.2 26.0 28.6 32.3 120.1 30.02534.7 33.3 26.2 31.6 125.8 31.4501 2 3 4 和 平均数Ⅳ Ⅲ Ⅱ Ⅰ窝 别 动物号因素也称为处理因素（factor ）（名义分类变量），每一处理因素至少有两个水平(level)（也称“处理组”）。

一个因素（水平间独立） ——单向方差分析（第八章）两个因素（水平间独立或相关）——双向方差分析（第九章）一个个体多个测量值——重复测量资料的方差分析 ANOV A 与回归分析相结合——协方差分析目的：用这类资料的样本信息来推断各处理组间多个总体均数的差别有无统计学意义。

单因素方差分析

单因素方差分析
3.如果系统误差明显地不同于随机误差，则均值就是 不相等的；反之，均值就是相等的
4.误差是由各部分的误差占总误差的比例来测度的。 当这个比值大到某种程度时，就可以说因素的不 同水平之间存在着显著差异，也就是自变量对因 变量有影响。
• 如本例，如果不同行业对被投诉次数没 有影响，那么在组间误差中只包含随机 误差，而没有系统误差。这时，组间误 差与组内误差经过平均后的数量就应该 很接近，它们的比值就会接近1。反之， 如果不同行业对被投诉次数有影响，在 组间误差中除了包含随机误差外，还会 包含系统误差。这时，组间误差平均后 的数值就会大于组内误差平均后的数值， 它们的比值就会大于1。
• 由于这里只涉及“行业”一个总体，因此称为单 因素四水平检验。
• 因素的每一个水平可以看做是一个总体，如零售 业、旅游业、航空公司、家电制造业可看作是四 个总体。上表中的数据可以看做是从这四个总体
• 在单因素方差分析中，涉及两个变量：一个 分类型自变量，一个数值型的因变量。如判 断“行业”对“被投诉次数”是否有显著影 响，这里“行业”就是自变量，是一个分类 型自变量，零售业、旅游业、航空公司、家 电制造业是“行业”这一变量的具体取值， 是“行业”这一因素的水平或处理 。
• “被投诉次数” 是一个数值型的因变量，不 同的被投诉次数就是因变量的取值。
• 方差分析就是判断分类型自变量对数值型因 变量的影响。在本例中就是研究“行业”对 “被投诉次数”的影响
方差分析的基本思想和原理
方差分析的图形分析
要判断“行业”对“被投诉次数”是否有显著影响，可通 过散点图来观察。下图中的折线是由被投诉次数的均值连 接而成的。
“行业”对“被投诉次数” 有显著影响
• 如果原假设成立，即H0 ： 1 = 2 = 3 = 4

生物统计学课件单因素方差分析

生物统计学课件单因素方差分析

(i
)]2
n a 1
E[
a i 1
( i.
..)2
2
a i1
( i.
..) (i
)
a i 1
(i
)2
]
处理均方的数学期望
n [E a 1
a i1
(i. )2
a
E
(
2 ..
)]
n a 1
a
2 i
i1
n (a 2
]
i 1
( E(ij ) 0,
E
(
2 ij
)
2
)
1 (an 2 na 2 )
an a
n
2
处理均方的数学期望
E ( MS A
)
a
1 1
E(SSA
)
1
a
E[
a 1 i1
n
( xi.
j1
x..)2 ]
1 a 1
E[n
a i 1
(
i
i.
..)2
]
n a 1
E
a i 1
[( i
..)
均方
称为处理间均方
MS A
SSA a 1
称为误差均方
MSe
SSe a(n 1)
为了估计σ2，除以相应的自由度而得到的
误差均方数学期望
E(MSe )
1 na
a
E(SSe )
1
a
E[
an a i1
n
( xi j xi. )2 ]
j1
1 an a
a
E[
i1
n i1
(
i
ij
i
i. )2 ]

第八章 方差分析(1)

第八章 方差分析(1)
2.处理内误差(sum of squares for error)，记为SSE § 因素的同一水平下数据误差的平方和 比如，施用A种氮肥下水稻产量的误差平方和
§ 只包含随机误差
3.处理间误差(sum of squares for category)，记为SSC § 因素的不同水平之间数据误差的平方和 比如，不同氮肥下水稻产量之间的误差平方和
2.由误差平方和除以相应的自由度求得 3.三个平方和对应的自由度分别是
▪ SST 的自由度为nk-1，其中nk为全部观察值的个数 ▪ SSt的自由度为k-1，其中k为因素水平的个数 ▪ SSe 的自由度为k（n-1）
8 - 21
第四章 概率论与抽样分布
8.1 方差分析概述
计算均方 MS
1.处理间均方：SSt的均方，记为MSt，计算公式为
▪SST=(242+302+…+212）-13833.8= 402.2
8 - 15
第四章 概率论与抽样分布
8.1 方差分析概述
处理间误差SSt
2、各组平均值 与x总i 平(i均值1,2的,离差, k平) 方和
x
反映各总体的样本均值之间的差异程度
该平方和既包括随机误差，也包括系统误差
计算公式为
ni
k
k
xij x 2 ni xi x 2
ni
xij xi 2
i1 j1
i1
i1 j1
SST = SSC + SSE
▪ 前例的计算结果
402.2=301.2+101.0
8 - 20
第四章 概率论与抽样分布
8.1 方差分析概述
均方(Mean square)
1.各误差平方和的大小与观察值的多少有关，为消除观察值 多少对误差平方和大小的影响，需要将其平均，这就是均 方，记为MS

单因素试验的方差分析

单因素试验的方差分析
2
j
μ 各个随机误差 ε ij 相互独立， 1 , μ 2 , , μ s 和 σ
未知.
单因素试验表 部分总体 样 本 A1 A2 … As
X11
X21
· · ·
X12 …
X22 … Xn22 … T.2 …
X 2
· · ·
X1s
X2s
· · ·
…
Xn11 样本和T.j 样本均值 X j T.1
是 σ 的无偏估计
.
结合定理(1)(2)(3)，有
F S A /( s 1 ) S E /( n s ) ~ F ( s 1, n s )
ST ，SA ，SE 的计算方法
n
j
记 T j 化简得

i1
X
ij
， T

j1 i1
s
2
s
n
j
X
ij

T
j1
s
j
j1 i1
s
n
j
(X
ij
X
j )
2
说明：
SE 表示在每个水平下的样本值与该水平下的样本 均值的差异，它是由随机误差引起的，所以，称SE是 误差（组内）平方和.
平方和分解公式：
ST S A S E
证明：S
i1
s
n
j
(X
ij
X)
2

( X
j1 i1
2
都是未知参数。
在水平Aj下进行nj次独立试验，得样本
X 1 j， X
2 j
， ，X
nj j
，
则
记
X
ij
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二节 固定效应模型
一、固定模型的方差分析程序
（一）假设
H 0 : 1 = 2 = L = a H A : 不是所有的 i都相等
即，
H 0 : α1 = α 2 = L = α a = 0 H A : 不是所有的 α i都等于 0
（二）确定显著性水平α
（三）计算统计量
S2 =
∑ (y
i =1
（四）方差分析的原理 （1）将数据的总变异分解为不同处理引起的变异（系统误差 或处理效应）和随机误差（试验误差）引起的变异 （2）通过F检验，比较不同处理引起的变异和随机误差引起 的变异的相对大小： 如果不同处理引起的变异明显比随机误差引起的变异 大，则说明不同处理确实有显著差异 如果不同处理引起的变异明显不比随机误差引起的变异 大，则说明不同处理没有显著差异
yaj
┇
n 组总和 组平均数
y1n y1.
y1
y2n y2.
y2
… … …
yin yi.
yi
… … …
yan ya.
ya
y ij 表示第 i个处理的第 j次观测值
y i =
∑y
j =1
n
ij
表示第 i 个处理所有数据的和
1 y i = y i 表示第i个处理所有数据的平均值 n
y = ∑∑ y ij 表示所有处理中全部数据的总和
2 i =1 i =1 j =1 i =1 j =1
a
a

a
n
j =1
∑ ( y ij y i ) = 0
n
=
n∑ ( y i y ) 2 + ∑∑ ( y ij y i ) 2
i =1 i =1 j =1
a
a
n
平方和的简易求法
SS T = ∑∑ y ij C
2 i =1 j =1 a n
n
i
y)
2
n 1 和处理内变异
，方差分析就是要把一个试验的总变异依据变异来源分解为处理间变异
y ij = α
总变异
i
+ ε
ij
不同处理引 起的变异
误差引起 的变异
方差分析的目的是分析不同处理引起的变异是否显著， 从而得出不同处理是否有显著差异。
1、平方和的计算和分解
y ij = α i + ε ij
（二）两类方差 1、处理内方差：在因素的同一水平（同一个总体）下，样本 数据的方差 2、处理间方差：因素的不同水平（不同总体）下，各样本之 间的方差。 （三）方差的比较 如果不同盐浓度对植株鲜重没有影响，则处理间方差就只包含 随机误差，处理内方差与处理间方差的比值接近1，反之， 则大于1，当大到某个程度时，就可以说不同水平之间存在 着显著差异。
4、显著性检验——F检验（上尾检验）
F( df A , df e ) = MS A MS e
（四）拒绝域的建立 （五）作出结论并给予相关知识领域的解释
例1，有一水稻施肥的盆栽 试验，设置了5个处理：A1和A2 分别施用 两种不同工艺流程的氨 水，A3 施碳酸氢氨， A4 施尿素，A5不施氮肥。 每个处理各 4盆，共有5 × 4＝20盆，随机置于同一盆栽 场，其稻谷产量 如下表。试求各平方和 ，自由度和均方。
∑α
i =1
a
i
= 0, 且每个α i是常数。
固定效应模型
i = + α i为第i个处理的平均数。
ε ij 是y ij的试验的随机误差（也称为噪声）。
我们假定ε ij 相互独立且服从正态分布N (0, σ 2 )。
因此，方差分析假定 y ij ～N ( + α i , σ 2 ), 这是方差分析的条件。
5、试验处理（treatment）：在试验对象上实施的事先设计好 的具体项目，简称处理。在进行单因素试验时，试验因素的一个
水平就是一个处理；对于双因素试验，处理的个数等于两个因素水平 个数的乘积。每个处理可以看做是一个总体，每个处理得到的一组数 据可以看做是从这个处理总体中抽取的一个样本的数据。
6、试验单位（experiment unit）：在试验中能接受不同试验 处理的独立的试验载体，是获得观测数据的单位。 7、重复（repetition）：在试验中，将一个处理实施在两个或 两个以上的试验单位上称为处理有重复，处理实施的试验 单位数目称为处理的重复数。观测数≠重复
第八章 单因素方差分析 （One－factor ANOVA)
ANOVA: Analysis of Variance
目的要求
掌握：方差分析的意义、功用与应用范围；多 重比较法及多重比较结果的表示法。 熟悉：不同类型单因素资料的方差分析方法。 了解：方差分析的线性模型和期望均方。统计 软件Excel、SPSS应用。
i =1 j =1 a n
1 y = y 全部数据的总平均值 an
注意：“”表示对一个下标的求和
（二）单因素试验的数据描述
yij 可表示成
yij = + α i + ε ij
其中，为全体试验值的总体平均数，
α i为第i个处理的效应，表示处理i对试验结果产生的影响。
如果我们只研究这a个不同处理，则有
i =1 j =1
a
n
ij
y ) = ∑∑ [( y i y ) + ( y ij y i )] 2
i =1 j =1
2
a
n
= ∑∑ [( y i y ) 2 + 2( y i y )( y ij y i ) + ( y ij y i ) 2 ]
i =1 j =1
a
n
= n∑ ( y i y ) + 2∑ [( y i y )∑ ( y ij y i )] + ∑∑ ( y ij y i )
答：常采用第五章里讲的t检验法。
现在，如何进行 a 个样本的平均数差异的假设检验（a ≥ 3）？
某人答：两两进行 t检验。
评论：这种方法是不行的。
主要原因有三：
原因（1）：检验的工作量大
当有a个样本平均数，两两组合，就有 a(a 1) 个平均数的差。 2
10 × 9 例如，a = 10时，就有 ＝45个平均数的差。 2
总变异
不同处理引 起的变异
随机误差引 起的变异
如何定量地衡 量这些变异？ 量这些变异？
2 ij
∑∑ ( y
i =1 j =1
a
n
2 ij
y )
n ∑ ( y i y )
i =1
a
2
∑∑ ( y
i =1 j =1
a
n
y i )
称为误差平方 误差平方 和，记为 SSe
称为总平方和 总平方和， 总平方和 记为 SST
2、随机效应模型 如果处理效应是由随机因素所引起的效应，就称为随机效 应。 固定因素是指因素的水平可以严格地人为控制，水平固定 后它的效应值也是固定的，实验重复时可以得到相同的结 果。 处理固定因素所用的模型称为固定效应模型，简称为固定 模型。 固定模型的方差分析所得到的结论只适合于选定的那几个 水平，并不能将其结论推广到其他未考虑的水平上。
2、混合模型 在多因素试验中，若即包括固定因素，有包括随机因素， 那么该实验应该用混合实验模型进行统计分析。
四、方差分析的原理：
（一）两类误差 1、随机误差：在因素的同一水平（同一个总体）下，各样 本的各观察值之间的差异。如同一盐浓度下的不同碱蓬植 株鲜重的差异 2、系统误差：在因素的不同水平（不同总体）下，各观察 值之间存在的差异。如不同盐浓度处理的碱蓬植株鲜重的 不同。
a = 2时只作一次假设检验， H 0 被接受的概率为 1 α＝0.95
I 型错误( H 0为真时，但却被我们否定)＝1－0.95 = 0.05
3 a = 3时作3次检验，H 0 被接受的概率为（ α） 0.953＝0.8574 1 ＝
I 型错误＝1－0.8574 = 0.1426
10 a = 5时作10次检验，H 0 被接受的概率为（1 α） ＝0.9510＝0.5987
换句话说，采用两两t检验法，要进行45次t检验，程序太繁琐。
原因（2）：检验的I 型错误增大，从而检验的 可靠性低
a = 2 时， H 0 只有一个，即
1＝ 2
a = 3 时， H 0 有 3 个，即 1＝ 2， 2＝ 3， 1＝ 3
a = 5时，H 0 有10个，即1＝ 2， 2＝3， , 4＝5 L
j =1 n
所以，自由度df e = an a = dfT df A
3、方差（均方）的计算
各平方和除以相应的自由度便得到总均方，处理均方，和误差均方，
分别记为 MST , MS A , MSe , 即
MS T SS T = df T
MS
A
SS A = df A
SS e MS e = df e
* 注意：MST ≠ MS A + MSe
三、方差分析的数学模型
（一）单因素试验的数据描述
重复数（j) 1 1 2 3
┇ j ┇
处理（组别） （i=1,2,...,a） 2 y21 y22 y23
┇
… … … …
┇
i yi1 yi2 yi3
┇
… … … …
┇
a ya1 ya2 ya3
┇
y11 y12 y13
┇
y1j
┇
y2j
┇
…
┇
yij
…
┇
（三）因素处理效应和实验模型的分类
1、固定效应模型 如果处理效应是由固定因素所引起的效应，就称为固定效 应。 随机因素是指因素的水平可以严格地人为控制，水平固定 后它的效应值也是固定的，实验重复时可以得到相同的结 果。 处理固定因素所用的模型称为固定效应模型，简称为固定 模型。随机效应模型的方差分析所得到的结论可以推广到 总体水平上