【全国百强校】内蒙古包头市第九中学2018届高三10月月考数学(文)试题(答案图片版)

2018年普通高等学校招生全国统一考试（包头市第一次模拟考试）文科数学一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设集合，，则（）A. B. C. D.【答案】A【解析】由题意，集合，则，故选A．2. 设复数满足，则（）A. B. C. D.【答案】B【解析】由题意复数满足，则，所以，故选B．3. 函数图象的一条对称轴是（）A. B. C. D.【答案】C【解析】由函数，令，解得，即函数图象的一条对称轴是，故选C．4. 已知向量，.若与平行，则（）A. B. C. D.【答案】D【解析】由向量，，则，因为向量与平行，则，解得，故选D．5. 在平面直角坐标系中，直线为双曲线的一条渐近线，则该双曲线的离心率为（）A. B. C. D.【答案】C【解析】由题意，双曲线的渐近线方程为，又直线是双曲线的一条渐近线，所以，所以，故选C．6. 若，且，则的最小值为（）A. B. C. D.【答案】D【解析】由题意，作出约束条件所表示的平面区域，如图所示，目标函数，可化为，由图可知，当直线过点时，得到目标函数的最小值，由，解得，则目标函数的最小值为，故选D．7. 某多面体的三视图如图所示，则该多面体的体积为（）A. B. C. D.【答案】C【解析】由题意知，根据给定的三视图可知，该几何体的左侧是一个底面为等腰直角三角形，且腰长为，侧棱长为的直三棱柱，右侧为一个底面为等腰直角三角形，且腰长为，高为的三棱锥，所以该几何体的体积为，故选C．8. 已知函数，则错误．．的是（）A. 在单调递增B. 在单调递减C. 的图象关于直线对称D. 的图象关于点对称【答案】D【解析】由函数，可得函数满足，解得，又函数，设，其开口向下，且对称轴为，所以函数在上单调递增，在上单调递减，根据复合函数的单调性可得在上单调递增，在上单调递减，且函数的图象关于直线对称，故选D．9. 某学生食堂规定，每份午餐可以在三种热菜中任选两种，则甲、乙两同学各自所选的两种热菜相同的概率为（）A. B. C. D.【答案】B【解析】由题意，甲同学选的两种热菜有种，两同学选的两种热菜有种，所以甲、乙两同学各自所选的两种热菜共有种，其中甲、乙两同学各自所选的两种热菜相同共有种情况，甲、乙两同学各自所选的两种热菜相同的概率为，故选B．10. 执行如图所示的程序框图，如果输入的，则输出的（）A. B. C. D.【答案】B【解析】模拟执行程序，可得，执行循环体，；满足条件，执行循环体，；满足条件，执行循环体，；满足条件，执行循环体，；满足条件，执行循环体，；满足条件，执行循环体，；此时不满足条件，退出循环，输出的值，故选B．点睛：算法时新课程的新增加的内容，也必然是新高考的一个热点，应高度重视，程序填空与选择是重要的考查和命题方式，这种试题考查的重点有：①条件分支结构；②循环结构的添加循环条件；③变量的赋值；④变量的输出等，其中前两点是考试的重点，此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．11. 现有张牌（1）、（2）、（3）、（4），每张牌的一面都写上一个数字，另一面都写上一个英文字母。

内蒙古包头市2018届高三第二次模拟数学文试题一、单项选择题（共12小题，每小题5分，满分60分）1．已经集合M={﹣1，0，1，2，3，4，5}，N={x|x≤1或x≥4}，则M∩N=（） A． {﹣1，0，1，4，5} B． {1，2，3，4}C． {﹣1，0，5} D．{﹣1，0，1，5}2．已知a∈R，i是虚数单位，若（a+i）（1+i）=2i，则a=（） A．﹣1 B． 1 C． 2 D．﹣23．已知等比数{an }满足a1a7=3a4a3，则数列{an}的公比q=（）A． 2 B．C． 3 D．4．已知两个平面α，β，直线l⊥α，直线m⊂β，有下面四个命题：①α∥β⇒l⊥m；②α⊥β⇒l∥m；③l⊥m⇒α∥β；④l∥m⇒α⊥β，其中正确命题有（）A．①②B．①④C．②③D．①③5．已知sin2α=，则sin2（α+）=（）A．B．C．D．6．如果执行如图所示的框图，输入N=5，则输出的数等于（）A．B．C． D．7．一个棱锥的三视图如图所示，则该棱锥的体积为（）A． 28 B．24 C．72 D．368．曲线y=e﹣2x+2在点（0，3）处的切线与直线y=0和y=x围成的三角形的面积为（）A．B．C．D．9．设x ，y 满足，则z=x+y 的最小值为（ ） A ．﹣8B ． ﹣7C ． ﹣6D ． ﹣5 10．设函数f （x ）=，则满足f （x ）≤3的x 的取值范围是（ ） A ． [0，+∞） B ． [﹣1，3]C ． [0，3]D ． [1，+∞） 11．设F 1，F 2分别是椭圆E ：+=1的左，右焦点，过F 1的直线l 与E 相交于A ，B 两点，且|AF 2|，|AB|，|BF 2|成等差数列，则|AB|=（ ）A ．B ． 3C ．D ． 212．已知函数y=的图象与函数y=kx ﹣2的图象恰有两个交点，则实数k 的取值范围是（ ） A ．（﹣2，﹣1）∪（0，4）B ． （0，）∪（，4）C ．（，1）∪（1，4）D ．（0，1）∪（1，4）二、填空题（共4小题，每小题5分，满分20分）13．设不等式组表示的平面区域为D ，在区域D 内随机取一个点，则此点到坐标原点的距离大于2的概率是 _________ ．14．在长方形ABCD 中，AD=1，E 为CD 的中点，若=﹣1，则AB 的长为 _________ ．15．已知sin （α+）=，α∈（，），则cos α= _________ ． 16．设等差数列{a n }满足a 3=5，a 10=﹣9，S n 是数列{a n }的前n 项和，则S n 的最大值为 _________ ．三、解答题（共5小题，共70分。

包头市一中2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题1． 线段AB 在平面α内，则直线AB 与平面α的位置关系是（ ）A ．AB ⊂αB ．AB ⊄αC ．由线段AB 的长短而定D ．以上都不对2． 2016年3月“两会”期间，有代表提出适当下调“五险一金”的缴存比例，现拟从某工厂职工中抽取20名代表调查对这一提案的态度，已知该厂青年，中年，老年职工人数分别为350，500，150，按分层抽样的方法，应从青年职工中抽取的人数为（ ） A. 5 B.6 C.7D.10【命题意图】本题主要考查分层抽样的方法的运用，属容易题. 3． 已知函数f(x)是定义在R 上的奇函数，当x ≥0时，.若,f(x-1)≤f(x),则实数a 的取值范围为A[] B[] C[]D[]4． 设等差数列{a n }的前n 项和为S n ，已知S 4=﹣2，S 5=0，则S 6=（ ）A ．0B ．1C ．2D ．35． 如图，1111D C B A ABCD -为正方体，下面结论：① //BD 平面11D CB ；② BD AC ⊥1；③ ⊥1AC 平面11D CB .其中正确结论的个数是（ ）A ．B ．C ．D ．6． 已知函数211,[0,)22()13,[,1]2x x f x x x ⎧+∈⎪⎪=⎨⎪∈⎪⎩，若存在常数使得方程()f x t =有两个不等的实根12,x x（12x x <），那么12()x f x ∙的取值范围为（ ）A ．3[,1)4B．1[8 C ．31[,)162 D ．3[,3)87． 已知抛物线C ：24y x =的焦点为F ，定点(0,2)A ，若射线FA 与抛物线C 交于点M ，与抛 物线C 的准线交于点N ，则||:||MN FN 的值是（ ）A． B． C．1: D(1 8．不等式≤0的解集是（ ）A ．（﹣∞，﹣1）∪（﹣1，2）B ．[﹣1，2]C ．（﹣∞，﹣1）∪[2，+∞）D ．（﹣1，2]9． 在△ABC 中，AB 边上的中线CO=2，若动点P满足=（sin 2θ）+（cos 2θ）（θ∈R），则（+）•的最小值是（ ）A ．1B ．﹣1C ．﹣2D ．010．若直线:1l y kx =-与曲线C ：1()1e xf x x =-+没有公共点，则实数k 的最大值为（ ） A ．－1 B ．12C ．1 D【命题意图】考查直线与函数图象的位置关系、函数存在定理，意在考查逻辑思维能力、等价转化能力、运算求解能力．11．已知实数y x ,满足不等式组⎪⎩⎪⎨⎧≤-≥+≤-5342y x y x x y ，若目标函数mx y z -=取得最大值时有唯一的最优解)3,1(，则实数m 的取值范围是（ ）A ．1-<mB ．10<<mC ．1>mD ．1≥m【命题意图】本题考查了线性规划知识，突出了对线性目标函数在给定可行域上最值的探讨，该题属于逆向问题，重点把握好作图的准确性及几何意义的转化，难度中等. 12．垂直于同一条直线的两条直线一定（ ）A ．平行B ．相交C ．异面D ．以上都有可能二、填空题13．在（1+2x ）10的展开式中，x 2项的系数为 （结果用数值表示）．14．设等差数列{a n }的前n 项和为S n ，若﹣1＜a 3＜1，0＜a 6＜3，则S 9的取值范围是 ．15．若点p （1，1）为圆（x ﹣3）2+y 2=9的弦MN 的中点，则弦MN 所在直线方程为 16．已知△ABC 的面积为S ，三内角A ，B ，C 的对边分别为，，．若2224S a b c +=+， 则sin cos()4C B π-+取最大值时C = ．三、解答题17．如图，已知椭圆C ：+y 2=1，点B 坐标为（0，﹣1），过点B 的直线与椭圆C 另外一个交点为A ，且线段AB 的中点E 在直线y=x 上 （Ⅰ）求直线AB 的方程（Ⅱ）若点P 为椭圆C 上异于A ，B 的任意一点，直线AP ，BP 分别交直线y=x 于点M ，N ，证明：OM •ON 为定值．18．已知函数()2ln f x x bx a x =+-.（1）当函数()f x 在点()()1,1f 处的切线方程为550y x +-=，求函数()f x 的解析式； （2）在（1）的条件下，若0x 是函数()f x 的零点，且()*0,1,x n n n N ∈+∈，求的值；（3）当1a =时，函数()f x 有两个零点()1212,x x x x <，且1202x x x +=，求证：()00f x '>．19．（本小题满分12分）已知平面向量(1,)a x =，(23,)b x x =+-，()x R ∈. （1）若//a b ，求||a b -；（2）若与夹角为锐角，求的取值范围.20．△ABC 中，角A ，B ，C 所对的边之长依次为a ，b ，c ，且cosA=，5（a 2+b 2﹣c 2）=3ab ．（Ⅰ）求cos2C 和角B 的值； （Ⅱ）若a ﹣c=﹣1，求△ABC 的面积．21．已知△ABC 的三边是连续的三个正整数，且最大角是最小角的2倍，求△ABC 的面积．22．已知函数f （x ）=．（1）求函数f （x ）的最小正周期及单调递减区间； （2）当时，求f （x ）的最大值，并求此时对应的x 的值．23．（本小题满分10分）选修4-4：坐标系与参数方程已知曲线C 的极坐标方程是2cos ρθ=，以极点为平面直角坐标系的原点，极轴为轴的正半轴，建立 平面直角坐标系，直线的参数方程是243x ty t=-+⎧⎨=⎩（为参数）.（1）写出曲线C 的参数方程，直线的普通方程； （2）求曲线C 上任意一点到直线的距离的最大值.包头市一中2018-2019学年上学期高三数学10月月考试题（参考答案）一、选择题1．【答案】A【解析】解：∵线段AB在平面α内，∴直线AB上所有的点都在平面α内，∴直线AB与平面α的位置关系：直线在平面α内，用符号表示为：AB⊂α故选A．【点评】本题考查了空间中直线与直线的位置关系及公理一，主要根据定义进行判断，考查了空间想象能力．公理一：如果一条线上的两个点在平面上则该线在平面上．2．【答案】C3．【答案】B【解析】当x≥0时，f（x）=，由f（x）=x﹣3a2，x＞2a2，得f（x）＞﹣a2；当a2＜x＜2a2时，f（x）=﹣a2；由f（x）=﹣x，0≤x≤a2，得f（x）≥﹣a2。

内蒙古包头市第九中学2018届高三10月月考文科综合历史试卷24．周初分封都有隆重的仪式，然后被分封的诸侯率领族人到达封地，建立军事据点，由点到面进行武装拓展，完成对封地的控制，据点叫“国”，国以外的土地叫“野”，“国”中之居民叫“国人”，“野”中之居民叫“野人”下列推断最正确的是（）A．“国”在西周发展为封建城市B．“野”的范围大小决定着诸侯国的地位C．“国人”多数是贵族的同族人D．“野人”的主要职责是拱卫京师25．宋太祖任命京官周渭到地方任知县，周渭到任时，大将符彦卿亲往城外迎接，但周渭仅在马上作揖，符彦卿极为不满又无可来何。

造成这一现象的主要原因是（）A．京官周渭对符彦關轻视B．周渭是来自京城的皇帝亲信C．中央集权制度的日益完善D．宋朝重文轻武的制度设计26．观察图，分析表中数据能得到的合理结论是（）A．经济发展水平与水旱灾害次数成正比B．隋唐政治制度完善导致水旱灾害较少C．农耕经济发展致使生态环境遭到破坏D．两宋时期水旱灾害较多导致经济倒退27．早在公元1000年左右，北欧诺曼人就曾远达冰岛、格陵兰和北美洲东岸。

但是诺曼人的发现并没有引起全球地理大发现，这是因为（）A．当时的欧洲商品经济不发达B．诺曼人到达的地方比较偏远C．诺曼人没有开辟通往中国与印度的新航线D．诺曼人没有带回资产阶级所需要的黄金与原料28．古希腊一些学者认为，城邦起源于人的“自保的要求”，正义、美德应该属于所有的人，法律和道德只有对人有好处时才能存在，才是真理。

他们还认为，法律不是自然存在的，是人为产生的，是由僭主制定的，法律的强制性违背了人的自然天性。

这些学者（）A．肯定了人的重要性B．重在论述法律制定应符合人的天性C．阐述了社会契约论D．正确分析了城邦制起源的历史原因29．一位在狱中受过军事队列训练的德国老鞋匠，在1906年刑满释放后的某日，打扮成一名少尉，带领在街头偶然遇到的一小队士兵，来到某镇财务所，说：“我是皇帝派来的，赶快把钱给我。

2018年内蒙古省包头市初中毕业、升学考试数 学（满分150分，考试时间120分钟）一、选择题：本大题共12小题，每小题3分，共36分．不需写出解答过程，请把最后结果填在题后括号内．1．（2018内蒙古包头，1，3分）计算34---的结果是( ) A.－1 B.－5 C.1 D.5 【答案】B【解析】原式＝－2－3＝－5，故选择B. 【知识点】实数的运算2．（2018内蒙古包头，2，3分）如图1，是由几个大小相同的小立方块所搭几何体的俯视图，其中小正方形中的数字表示在该位置的小立方块的个数，则这个几何体的主视图是( )【答案】C【解析】主视图是指从正面看到的图形，由已知条件可知，主视图有两列，每列小正方形数目分别是2、2，故选择C. 【知识点】几何体的三视图3.（2018内蒙古包头，3，3分） 函数11-=x y 中，自变量x 的取值范围是( )A.x ≠1B.x >0C.x ≥1D.x >1【答案】D【解析】根据函数有意义，则分母不能为0，根号下的数必须非负得:x －1>0，所以x >1，故选择D.【知识点】函数自变量的取值范围4．（2018内蒙古包头，4，3分） 下列事件中，属于不可能事件的是( ) A.某个数的绝对值大于0 B.某个数的相反数等于它本身 C.任意一个五边形的外角和等于540°D.长分别为3，4，6的三条线段能围成一个三角形 【答案】C【解析】根据定义可知：A 、B 都属于随机事件；C 属于不可能事件；D 属于确定必然事件.故选择C.【知识点】事件的分类及概念5．（2018内蒙古包头，5，3分）如果y a x 12+与12-b y x 是同类项，那么b a的值是( )A.21 B.23C.1D.3【答案】A【解析】根据同类项的特征可得⎩⎨⎧=-=+1121b a ，解得⎩⎨⎧==21b a ，∴21=b a .故选择A.【知识点】同类项的概念6．（2018内蒙古包头，6，3分）一组数据1，3，4，4，4，5，5，6的众数和方差分别是( ) A.4，1 B.4，2 C.5，1 D.5，2 【答案】B【解析】因为4出现了3次，次数最多，故众数是4； 又∵4865544431=+++++++=x ，∴282)46(2)45(2)45(2)44(2)44(2)44(2)43(2)41(2=-+-+-+-+-+-+-+-=S .故选择B.【知识点】众数、方差7．（2018内蒙古包头，7，3分）如图2，在△ABC 中，AB =2，BC =4，∠ABC =30°，以点B 为圆心，AB 长为半径画弧，交BC 于点D ，则图中阴影部分的面积是 ( )A.32π-B.62π-C.34π-D.64π-【答案】A【解析】作AM ⊥BC 于点M ， ∵∠ABC ＝30° ∴AM ＝21AB ＝1 3236022301421ππ-=⨯-⨯⨯=-∆=ABD SABC S S 扇形阴影面积故选择A.【知识点】扇形面积的计算；三角形面积的计算；含有30°角的直角三角形的性质8．（2018内蒙古包头，8，3分）如图3，在△ABC 中，AB ＝AC ， △ADE 的顶点D 、E 分别在BC 、AC 上，且∠DAE ＝90°，AD ＝AE .若∠C +∠BAC ＝145°，则∠EDC 的度数为( ) A.17.5° B.12.5° C.12° D.10°【答案】D【思路分析】由∠C +∠BAC ＝145°得知∠B ＝35°；由AB ＝AC 得知∠B ＝∠C ＝35°；由等腰直角三角形的性质可得∠AED ＝45°，又∵∠AED ＝∠EDC +∠C ，∴∠EDC ＝45°－35°＝10°.【知识点】等腰三角形的性质；等腰直角三角形的性质；三角形内角和；三角形外角的性质9．（2018内蒙古包头，9，3分）已知关于x 的一元二次方程0222=-++m x x 有两个实数根，m 为正整数，且该方程的根都是整数，则符合条件的所有正整数m 的和为 ( ) A.6 B.5 C.4 D.3 【答案】B【思路分析】根据方程有两个实数根，得出根的判别式的值大于或等于0列出关于m 的不等式，求出不等式的解集得到m 的取值范围；找出m 范围中的正整数解确定出m 的值，经检验即可得到满足题意的m 的值.【解题过程】根据题意得：△＝4－4（m －2）≥0，解得m ≤3； 由m 为正整数，得m ＝1或2或3， 利用求根公式表示出方程的解为m m x -±-=-±-=312)3(42，∵方程的解为整数。

包九中2017-2018学年度第一学期期中考试高三数学（理）一、选择题(本题共12小题，每小题5分，共60分) 1．设集合{}1,2,4A =，{}240B xx x m =-+=．若{}1AB =，则B =( )A ．{1，﹣3}B ．{1，0}C ．{1，3}D ．{1，5} 2．下列各式的运算结果为纯虚数的是( )A ．i （1+i ）2B ．i 2（1﹣i ）C ．（1+i ）2D ．i （1+i ） 3．下列说法不正确的是( )A ．若“p 且q”为假，则p ，q 至少有一个是假命题B ．命题“∃x ∈R ，x 2﹣x ﹣1＜0”的否定是““∀x ∈R ，x 2﹣x ﹣1≥0”C ．当a ＜0时，幂函数y=x a 在（0，+∞）上单调递减D ．“φ=”是“y=sin（2x+φ）为偶函数”的充要条件4．已知O 为坐标原点，点M 坐标为（﹣2，1），在平面区域上取一点N ，则使|MN|为最小值时点N 的坐标是( )A ．（0，0）B ．（0，1）C ．（0，2）D ．（2，0） 5．记等比数列{a n }的前n 项积为T n (n ∈N *)，已知1120m m m aa a -+⋅-=，且21128m T -=，则m 的值为( )A ．4B ．7C ．10D ．12 6．矩形A B C D 中，2A B =，1A D =，E 为线段B C 上的点，则A E D E ⋅的最小值为( )A ．2B ．154C ．174D ．47．函数()131lo g 1xx f x x x ⎧≤⎪=⎨>⎪⎩，则()4y f x x =+-零点个数为( )A.1B.2C.3D.4 8．已知△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，若cos 1cos b A cC=+，则s in 26A π⎛⎫+⎪⎝⎭的取值范围是( )A ．11,22⎛⎫-⎪⎝⎭B ．1,12⎛⎤-⎥⎝⎦C ．1,12⎛⎤⎥⎝⎦D ．11,2⎡⎫-⎪⎢⎣⎭9．()f x 是定义在R 上的奇函数，满足()()2f x f x +=，当()0,1x ∈时，()21xfx =-，则()12lo g6f的值等于( )A ．12- B ．6- C ．56- D ．4- 10．用数学归纳法证明不等式“()()()112221223n n n n n -⋅+-=⋅⋅-”()2n n N *≥∈且，从“n k =”到“1n k =+”时，左侧应添加的式子为( ) A ．21k - B ．23k - C ．()223k - D ．()221k - 11．平面内凸四边形有2条对角线，凸五边形有5条对角线，以此类推，凸13边形的对角线条数为( )A ．42B ．65C ．143D ．169 12．函数f （x ）=sin ωx+cos ωx+1的最小正周期为π，当x ∈[m ，n]时，f （x ）至少有12个零点，则n ﹣m 的最小值为( ) A ．12π B ．73π C ．6π D ．163π二、填空题(本题共4小题，每小题5分，共20分)13．函数y=log a （x+2）﹣1（a ＞0，a ≠1）的图象恒过定点A ，若点A 在直线mx+ny+1=0上，其中m ＞0，n ＞0，则+的最小值为 . 14．)10x d x⎰= .15．等差数列{a n }、{b n }的前n 项和分别为S n 与T n ，若5623a b =，则911=S T ．16．设函数()y f x =在区间(),a b 上的导函数为()'f x ，()'f x 在区间(),a b 上的导函数为()''f x ，若在区间(),a b 上()''0f x <恒成立，则称函数()f x 在区间(),a b 上为“凸函数”．已知()4321131262f x x m x x=--，若对任意的实数m 满足2m ≤时，函数()f x 在区间(),a b 上为“凸函数”，则b a -的最大值为 .三、解答题(共70分，第17—21为必考题，每题12分，22、23为选考题，每题10分)17．在△ABC 中，内角A ，B ，C 所对的边长分别是a ，b ，c ． （Ⅰ）若2c =，3Cπ=，且△ABC 的面积，求a ，b 的值；（Ⅱ）若()sin sin sin 2C B A A +-=，试判断△ABC 的形状． 18．已知函数()221c o ssin2f x x x =-+，()0,x π∈．（1）求()f x 的单调递增区间； （2）设△ABC 为锐角三角形，角A 所对边a=，角B 所对边b=5，若()0f A =，求△ABC 的面积．19．已知数列{}na 满足：16a=，()11036n n aa n N*+=+∈，数列{}nb 满足()4n n b a n N*=+∈.(1)求证：数列{}nb 是等比数列. (2)若11lg lg nn n cb b +=⋅()n N *∈，求证：数列{}n c 的前n 项和1nT<.20．数列{}na 为公差不等于零的等差数列，其前n 项和nS 满足530S=，且1a 、3a 、9a 成等比数列．（Ⅰ）求数列{a n }的通项公式； （Ⅱ）数列{b n }满足，求{b n }通项公式；（Ⅲ）令（n ∈N *），求数列{c n }的前n 项和T n ．21．设函数f （x ）=ax 2﹣a ﹣lnx ，g （x ）=﹣，其中a ∈R ，e=2.718…为自然对数的底数．（Ⅰ）讨论f （x ）的单调性； （Ⅱ）证明：当x ＞1时，g （x ）＞0；（Ⅲ）若f （x ）＞g （x ）在（1，+∞）内恒成立，求a 取值范围． 22、23为选考题，考生任选一题作答。

包头市第九中学2015-2016学年第一学期十月月考高一数学试卷试卷说明:本卷满分150分，考试时间120分钟. 一、选择题.（共12小题，每题5分）1、若{}1,2,3,4,5U =，{}1,2M =，{}2,3N =，则()N M C U Y 非空真子集个数为 A 、1 B 、2C 、3D 、42、下列七个说法①任何集合至少有两个子集；②{}{},,a b b a ⊆；③{}0=∅；④{}0∅⊆；⑤{}∅⊆∅；⑥{}∅∈∅；⑦0∅=∅I ， 其中正确的有 A 、2个B 、3个C 、4个D 、5个3、设{}2P x y x==，(){}2,Q x y y x ==，则P 、Q 之间关系为A 、P Q =∅IB 、P Q ⊇C 、P Q ⊆D 、P Q =4、设集合{}|22M x x =-≤≤，{}|02N y y =≤≤，给出下列四个图形，其中能表示以集合M 为定义域，N 为值域的函数关系的是5、函数1()2x f x x -=-的定义域为A 、()()1,22,+∞UB 、[)()1,22,+∞UC 、[)1,2D 、[)1,+∞ 6、下列四组函数，表示同一函数的一组是 A 、2y x y x ==与B 、11111x x y x y x x +≥-⎧=+=⎨--<-⎩与C 、2y x y x =与D 、2422y x y x x =-=+-与7、23y ax bx =++在(],1-∞-上单调递增，在[)1,-+∞上单调递减，则 A 、b>0且a<0 B 、b=2a>0 C 、b=2a<0D 、a 、b 符号不确定MNI8、已知非空集合{}2135A x a x a =+<≤-，{}322B x x =<≤，若A B ⊆成立，则实数a 的取值为 A 、()6,9B 、(],9-∞C 、(),9-∞D 、(]6,99、如果奇函数f(x)在区间[3，7]上是增函数且最小值为5，那么f(x)在区间[－7，－3]上是A 、增函数且最大值为－5B 、增函数且最小值为－5C 、减函数且最小值为－5D 、减函数且最大值为－510、()y f x =为R 上偶函数，且在[)0,+∞上单调递减，若()()2f a f ≥-，则a 的取值范围是A 、2≤aB 、2≥aC 、22≥-≤a a 或D 、22≤≤-a 11、已知()y f x =为偶函数，()y g x =为奇函数，它们定义域()()0f x g x ≤都是[]3,3-，且它们在[]0,3上的图像如图所示，则的解集是A 、[)[)[)2,10,12,3--U UB 、[)()[)2,10,12,3--U UC 、(]()()[)3,21,00,12,3---U U UD 、[][][]2,10,12,3--U U12、()201110211x x f x x x x xx x +≤<⎧⎪⎪=-<<⎨⎪≥≤-⎪⎩或，若方程()f x m =有两个不同实根，则实数m 取值范围为A 、()[),22,3-∞-UB 、(][],22,3-∞-UC 、(][],21,3-∞-UD 、(][),22,3-∞-U二、填空题（共8题，每题5分） 13、()f x 的图像如右图，则()f x 的值域为 .14、全集I 是R ，(]()1,02,M =-+∞U 与()2,2-=N 都是I 的子集，则下图阴影部分所表示的集合为 .15、集合{}22530M x x x =--=，{}1N x mx ==，若N M ⊆，则实数m 的取值集合xy321O()y f x =()y g x =为 .16、已知)(x f 为偶函数。

内蒙古包头市数学高三上学期理数 10 月月考试卷姓名:________班级:________成绩:________一、 单选题 (共 12 题；共 24 分)1. （2 分） 设全集 U={1,2,3,4,5}，集合 A={1,3},B={3,5}，则（）A . {1,4}B . {1,5}C . {2,4}D . {2,5}2. （2 分） 计算 的结果是（ ） A.i B . -i C.2 D . -23. （2 分） 已知△ABC， A.1 B.2 C.3 D.4则△ABC 的面积为（ ）4. （2 分） (2017 高二下·沈阳期末) “ A . 充分不必要条件 B . 必要不充分条件”是“”的（ ）第 1 页 共 12 页C . 充分必要条件 D . 既不充分也不必要条件 5. （2 分） 一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个 圈依此规律继续下去,得到一系列的圈,那么在前 120 个圈中的●的个数是（ ） A . 12 B . 13 C . 14 D . 156. （2 分） (2019 高一上·榆林期中) 已知函数 A . 有最大值 ，但无最小值 B . 有最小值 ，有最大值 1，的最值情况为（ ）C . 有最小值 1，有最大值 D . 无最大值，也无最小值7. （2 分） 定义在 R 上的奇函数 f（x）满足 f（x+1）=f（﹣x），当 x∈（0，1）时，f（x）=，则 f（x）在区间（1， ）内是（ ）A . 增函数且 f（x）＞0B . 增函数且 f（x）＜0C . 减函数且 f（x）＞0D . 减函数且 f（x）＜08. （2 分） (2019 高三上·鹤岗月考) 如图，在△中，点是线段 上两个动点，且第 2 页 共 12 页，则的最小值为（ ）A. B.C. D.9. （2 分） (2016 高二下·芒市期中) 已知等比数列{an}满足 A.2 B.1，a3a5=4（a4﹣1），则 a2=（ ）C.D. 10. （2 分） (2016 高一下·东莞期中) 若某程序框图如图所示，则输出的 p 的值是（ ）第 3 页 共 12 页A . 21 B . 26 C . 30 D . 5511. （2 分） (2016 高一下·朝阳期中) 已知 α，β 都是锐角，cosα= 值为（ ），cos（α+β）=﹣，则 oosβA.-B.-C.D. 12. （2 分） 下列推理是归纳推理的是（ ） A . A，B 为定点，动点 P 满足|PA|＋|PB|＝2a>|AB|，则 P 点的轨迹为椭圆 B . 由 a1＝1，an＝3n－1，求出 S1 ， S2 ， S3 ， 猜想出数列的前 n 项和 Sn 的表达式C . 由圆 x2＋y2＝r2 的面积 πr2 ， 猜想出椭圆的面积 S＝πab第 4 页 共 12 页D . 利用等差数列的性质推理得到等比数列的相关性质二、 填空题 (共 4 题；共 4 分)13. （1 分） (2019·呼伦贝尔模拟) 若满足，则目标函数的最大值为________.14. （1 分） (2016 高二下·宝坻期末) 已知 tanα=2，tan（α+β）=﹣1，则 tanβ=________．15. （1 分） 已知 x＜ ，则函数 y=2x+的最大值是________．16. （1 分） (2020 高一下·宣城期末) 函数三、 解答题 (共 7 题；共 70 分)17. （10 分） (2019 高一下·大庆期中) 在 .（1） 求角 ;的零点个数为________. 中,角 , , 的对边分别为 , , ,且（2） 若,且的面积为,求 的值.18. （10 分） (2019 高一上·绍兴期末) 已知函数Ⅰ求的最小正周期和单调递增区间；Ⅱ 把函数图象上的所有点向右平移 个单位长度得到函数的图象，求的解析式．19. （10 分） (2019 高一下·江东月考) 已知等差数列 满足：，前 n 项和为 ．（1） 求 及 ；（2） 设是首项为 1，公比为 3 的等比数列，求数列 的前 项和 .20. （10 分） (2020·龙岩模拟) 已知.，数列 的（1） 证明在处的切线恒过定点；第 5 页 共 12 页（2） 若有两个极值点，求实数 a 的取值范围.21. （10 分） (2018 高三上·重庆期末) 已知函数 （I）求 的取值范围；存在唯一极值点。

包九中高三语文月考试题本试卷分第Ⅰ卷(阅读题）和第Ⅱ卷（表达题)两部分地.满分150分，考试时间150分钟。

第Ⅰ卷阅读题（70分）一、现代文阅读（35分）（一）论述类文本阅读（9分，每小题3分)阅读下面的文字，完成1~3题。

儒家生态伦理思想的现实意义蔡方鹿当前，建设生态文明已成为全社会的共识。

解决环境污染和生态破坏带来的突出问题,全面提高我国生态文明建设水平,是实现中华民族可持续发展的治本之策。

对此,儒家生态伦理思想可提供有益借鉴。

在儒家博大精深的思想体系里，蕴含着丰富的生态伦理思想.在自然观上，儒家重视人与自然和谐统一，认为人是自然界的一部分，天人是相通的，提倡“天人合一”“仁者以天地万物为一体”,注意保护人类赖以生存的自然环境。

这些思想与西方文化强调征服自然、人与自然对立二分的观念形成鲜明对照.儒家历来反对滥用资源。

孔子明确提出“节用而爱人，使民以时”的思想.荀子把对山林川泽的管理、对自然资源的合理开发与保护作为“圣王之制”的内容，要求砍伐和渔猎必须遵守一定的时节，并规定相应的“时禁"期,以保护生物和资源。

儒家认为,对待天地万物，应采取友善、爱护的态度;自然资源是人类赖以生存的物质基础，如果随意破坏、浪费资源，就会损害人类自身。

孔子说：“伐一木,杀一善，不以其时，非孝也。

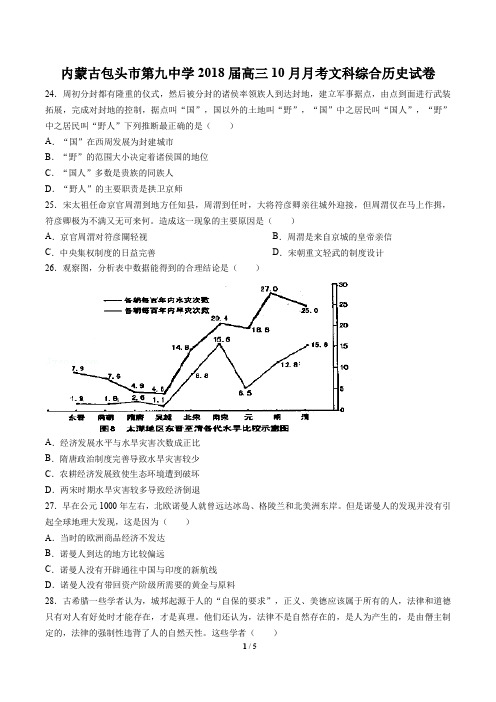
"孟子主张把人类之爱施与万物。

他说：“亲亲而仁民，仁民而爱物."朱熹进一步阐发了爱物的思想,他说：“此心爱物,是我之仁;此心要爱物，是我之义。

”儒家的生态伦理思想给今天的人们带来有益启示，那就是在发展经济、开发自然、利用资源的同时，必须注意人与自然关系的协调，把发展经济、发展科技与生产力同保护生态环境有机统一起来，把人类生活需要与生态环境运行规律有机结合起来，提高开发自然、利用资源的科学性与合理性。

当前,我们解决资源短缺问题，合理利用和有效保护资源，可以借鉴儒家所倡导的取用有节、物尽其用的思想。

高三10月份月考试卷(文）（时间120分，总分150分）一．选择题(每小题5分,共60分）1．在右边图中，设全集集合分别用椭圆内图形表示，若集合，则阴影部分图形表示的集合为（）A。

B.C. D。

2．设，为复数,则=（）A. B. C。

D。

3．中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难，次日脚痛减一半，六朝才得其关，要见次日行里数,请公仔细算相还。

”其意思是“有一个人走378里，第一天健步行走，从第二天起脚痛每天走的路程是前一天的一半，走了6天后到达目的地."请问第三天走了（）A. 60里B. 48里C. 36里D. 24里4．设，已知向量，,，且和，则（）A. B.C。

D.5．若变量满足约束条件，且的最小值为，则( ）A. 9 B 。

3 C.D 。

6。

若等比数列的各项都是正数，且成等差数列,则（ ）A. B 。

C. D 。

7． 函数的部分图象如图所示， 将的图象向左平移个单位后的解析式为（ )A. B 。

C 。

D.8。

已知，，,则=( ）A ．B ．C ．D ．—9．已知函数()2f x xax =-的图像在点()()1,1A f 处的切线与直线320x y ++=垂直,执行如图所示的程序框图，输出的k 值是( ）A 。

5B 。

6C 。

7D 。

810.在正项等比数列{a n }中，a 2017=a 2016+2a 2015．若a m a n =16a 12，则4m+1n 的最小值等于( )A 。

1 B. 35 C 。

32 D. 13611. 如图，在正方形ABCD 中，M 、N 分别是BC 、CD 的中点，若 =λ+μ，则λ+μ=（ ）A ．2B ．C ．D ．12. 已知()f x 是定义在R 上周期为2的偶函数,当[]0,1x ∈时，有()21x f x =-,则函数()()5log g x f x x=-的零点个数是（ )KS5UKS5U][KS5UKS5UKS5U]A 。