下载文档原格式
刚体的定轴转动定律1. 介绍刚体是物理学中的一个重要概念，它指的是在运动过程中形状和大小保持不变的物体。
刚体的定轴转动定律是描述刚体绕固定轴线转动的规律和性质，对于我们理解刚体的运动和应用相关物理问题具有重要意义。
2. 刚体的转动惯量2.1 定义刚体绕轴线转动时，其转动惯量是衡量刚体抵抗转动运动的特性。
转动惯量的大小取决于刚体的质量分布以及轴线的位置和方向。
2.2 转动惯量的计算方法转动惯量可以通过积分计算得到，对于一个质量为m的刚体，其转动惯量可以用以下公式表示： [ I = r^2 dm ] 其中，r是质量元dm到转轴的距离。
对于一些常见的简单形状的刚体，转动惯量可以通过一些公式直接计算得到，例如：- 细杆绕直线轴线转动：[ I = mL^2 ] - 球体绕直径轴线转动：[ I = MR^2 ] - 圆环绕直径轴线转动：[ I = MR^2 ]3. 定轴转动的角动量3.1 定义角动量是描述物体转动的物理量，刚体的角动量可以通过转动惯量和角速度的乘积得到。
3.2 角动量的守恒对于一个孤立系统，如果没有外力矩作用，刚体的角动量将保持不变，这就是角动量守恒定律的内容。
3.3 角动量定理角动量定理描述了外力矩对刚体角动量的影响，它可以表示为以下公式： [ = ] 其中，()是作用在刚体上的外力矩，(L)是刚体的角动量。
4. 牛顿第二定律与角加速度4.1 牛顿第二定律牛顿第二定律描述了刚体转动的加速度与作用力的关系，其公式为： [ = I] 其中，()是作用在刚体上的合外力矩，(I)是刚体的转动惯量，()是刚体的角加速度。
4.2 角加速度的计算对于旋转轴与力矩不垂直的情况，我们可以通过以下公式计算刚体的角加速度：[ = ] 其中，()是力矩与旋转轴之间的夹角。
5. 定轴转动的动能5.1 定义刚体的转动动能是由于其转动而具有的能量，它可以通过转动惯量和角速度的平方的乘积得到。
5.2 动能定理动能定理描述了外力对刚体转动动能的影响，它可以表示为以下公式： [ W = K ] 其中，(W)是作用在刚体上的合外力所做的功，(K)是刚体的转动动能。
刚体定轴转动概述刚体定轴转动是力学中的重要概念之一，用于描述刚体绕固定轴线旋转的运动形式。
本文将对刚体定轴转动进行概述，介绍其基本概念、定律和运动方程。
一、刚体定义与特点在力学中，我们将形状和大小不变的物体称为刚体。
与之相对的是流体，流体具有流动性质。
刚体的定义特点是：既能保持形状，又能在空间内绕固定轴线旋转。
二、刚体定轴转动的基本概念1. 轴线：刚体绕其旋转的直线称为轴线，轴线可以是直线也可以是曲线。
2. 物体上的任意一点：在刚体定轴转动中，我们可以选择物体上的任意一点作为参考点，称为转轴或转动中心，用O表示。
3. 角位移：刚体定轴转动时，转动中心O和物体上的任意一点P之间的角位移用Δθ表示。
4. 刚体转动惯量：刚体定轴转动惯量是描述刚体惯性特性的物理量，用I表示。
三、刚体定轴转动的定律1. 转动惯量定律：转动惯量I定义为刚体对绕轴线转动的惯性特性的度量。
根据转动惯量定律，转动惯量I与刚体的质量分布以及轴线相对于质心的位置有关。
2. 角动量守恒定律：刚体定轴转动时，其角动量L守恒。
角动量L的大小等于刚体转动惯量I乘以角速度ω，即L=Iω。
四、刚体定轴转动的运动方程在刚体定轴转动中，我们可以利用牛顿第二定律推导出运动方程。
根据牛顿第二定律，物体所受合外力的矩等于转动惯量I乘以角加速度α，即Στ=Iα。
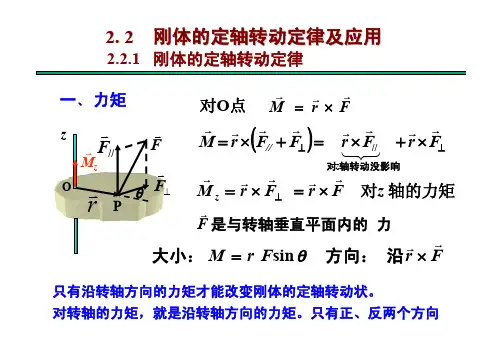
其中，Στ表示合外力对转动中心O产生的合力矩，相当于力对于轴线的力矩。
五、刚体定轴转动的应用刚体定轴转动在物理学中有着广泛的应用。
例如，在机械工程中，我们可以利用刚体定轴转动理论研究机械零件的稳定性和运动方式；在体育运动中，刚体定轴转动理论也被用来解释各种运动技巧和动作。
结语刚体定轴转动是力学中的重要概念，通过本文的概述，我们对刚体定轴转动的基本概念、定律和运动方程有了更深入的了解。
刚体定轴转动的研究对于解释和预测物体的旋转运动具有重要意义，也为相关学科的发展提供了理论基础。
刚体的定轴转动定律1. 引言刚体是物理学中的重要概念，它是由无穷多个质点组成的一个物体，质点间的距离在运动过程中保持不变。
刚体的运动可以分为平动（刚体作为一个整体的直线运动）和转动两种。
本文将着重讨论刚体的转动运动，特别是定轴转动定律。
2. 定轴转动定轴转动是指刚体绕固定轴线进行转动的现象。
例如，摆锤在一根细线上摆动、地球自转等都是定轴转动的例子。
在定轴转动中，我们需要了解刚体受力及其运动规律。
3. 转动定律的基本概念在讨论转动定律之前，我们先来了解一些基本概念：•角度：表示物体转动的程度，常用弧度制表示，符号为θ。
•角速度：表示物体单位时间内转过的角度，常用弧度/秒表示，符号为ω。
•角加速度：表示物体单位时间内角速度的变化率，常用弧度/秒^2表示，符号为α。
•转动惯量：表示刚体对转动的惯性大小，常用字母I表示。
4. 转动定律的表述转动定律是描述刚体转动运动情况的基本定律，其中最著名的有三个定律，即牛顿定律。
它们分别是：第一定律：角动量守恒定律“在没有外力作用下，刚体的角动量保持不变。
”所谓角动量守恒，就是指一个刚体在没有外力作用下的转动过程中，其角动量保持不变。
即刚体绕某一轴线转动时，如果没有外力矩作用，那么刚体的角动量始终保持恒定。
第二定律：动能定理“刚体的角动能变化等于外力矩做功的大小。
”对于旋转的刚体来说，其具有转动惯量以及角速度，因此可以存在角动能。
根据动能定理，一个刚体的角动能的变化等于作用在刚体上的外力矩所做的功。
第三定律：力矩定律（欧拉定律）“刚体转动的加速度与合外力矩成正比，与刚体转动惯量成反比。
”欧拉定律指出了刚体转动的加速度与作用力矩的关系，其数学表达式为：τ = I * α其中，τ表示作用在刚体上的合力矩，I表示刚体的转动惯量，α表示刚体的角加速度。
5. 转动定律的应用转动定律在物理学中有广泛的应用，以下是几个常见的应用场景：•摆锤运动：根据转动定律，可以推导出摆锤的周期与摆长、重力加速度的关系。
