当前位置：文档之家 › 4-2 刚体定轴转动的描述

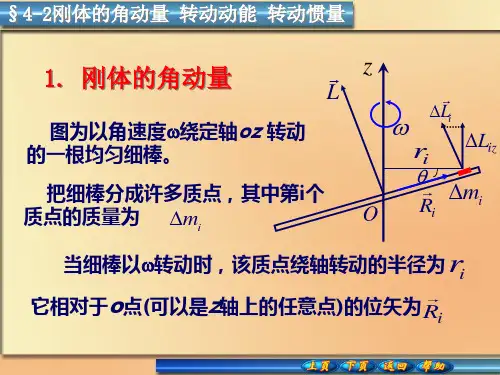
4-2 刚体定轴转动的描述

  • 格式：ppt
  • 大小：342.50 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

4第四章定轴转动

4第四章定轴转动

(4) 转动中M = Jα与平动中F = ma
地位相同．
（5） M = Jα = J dω
dt
30
三 转动惯量 ¾ 刚体的转动惯量等于刚体上各质点的质量与各质 点到转轴距离平方的乘积之和。
∑ ∫ J = Δm jrj2 J = r2dm j
¾ 转动惯量的单位：kg·m2 ¾ J 的意义：转动惯性的量度 .
2π 2π
19
（2）t = 6 s时，飞轮的角速度
ω
=
ω0
+
αt
=
(5π
−
π 6
×
6)
=
4π
rad⋅
s−1
（3）t = 6 s时，飞轮边缘上一点的线速度大小
v = rω = 0.2× 4π = 2.5 m ⋅s−2
该点的切向加速度和法向加速度
at
=
rα
=
0.2× (−
π) 6
=
−0.105
m ⋅s−2
轮与轴承间的摩擦力可略去不计．
A
(1)两物体的线加速度为
mA
C
mC
多少？ 水平和竖直两段绳索 的张力各为多少？(2) 物体 B
从静止落下距离 y 时，其速
mB B 率是多少？
40
解 (1) 用隔离法分
别对各物体作受力分析，
取如图所示坐标系．
A
mA v FN v
mA FT1
vO x
PA
C
mC
mB B
18
解（1）ω0 = 5π rad ⋅ s−1, t = 30 s 时，ω = 0
设 t = 0 s 时，θ0 = 0 ，飞轮作匀减速运动
α = ω − ω0 = − π rad ⋅s−2
刚体的转动

刚体的转动

2） 任一质点运动 ,, 均相同，但 v, a 不同；
32019/12/23
§4- 1 刚体的平动、转动和定轴转动 普通物理
二 匀变速转动公式 当刚体绕定轴转动的角加速度为恒量时，刚体做
匀变速转动 .
刚体匀变速转动与质点匀变速直线运动公式对比
地减速，经t=50 s后静止。
（1）求角加速度a 和飞轮从制动开始到静止所转过
的转数N；
（2）求制动开始后t=25s 时飞
0
轮的角速度 ；
（3）设飞轮的半径r=1m，求在 t=25s 时边缘上一点的速
度和加速度。
Oa an r
v
at
解 （1）设初角度为0方向如图所示，
广东技术师范学院
2019/12/23
25rad / s 78.5rad / s
广东技术师范学院
2019/12/23
§4- 1 刚体的平动、转动和定轴转动 普通物理
的方向与0相同 ；
（3）t=25s 时飞轮边缘上一点P 的速度。
由 v r v v r sin r sin 900
r 78.5m / s v 的方向垂直于 和 r 构成的平面，如
§4- 1 刚体的平动、转动和定轴转动 普通物理
量值为0=21500/60=50 rad/s，对于匀
变速转动，可以应用以角量表示的运动方程，在
t=50S 时刻 =0 ，代入方程=0+at 得
a 0 50 rad / s2
t
50
3.14 rad / s2
从开始制动到静止，飞轮的角位移 及转 数N 分别为
子的角加速度与时间成正比 . 问在这段时间内，转子转
过多少转？
刚体的定轴转动

刚体的定轴转动


J
1 2 m( R12 R2 ) 2
1 mR 2 2 若R1 R2 R, J mR 2
16
例：求长度为L，质量为m的均匀细棒AB的转动惯量。 （1）对于通过棒的一端与棒垂直的轴。 （2）对于通过棒的中心与棒垂直的轴。 m 解（1）细杆为线质量分布，单位长度的质量为： l L 1 3 2 2 dm A B J A x dm x dx L o 0 3 x
2 0
2

0
dm MR
2
绕圆环质心轴的转动惯量为
M
o
R
பைடு நூலகம்dm
J MR
2
讨论：若圆环绕其直径轴转动，再求此圆环的转动 惯量。
14
例: 一质量为m，半径为R的均匀圆盘，求对通过盘 中心并与盘面垂直的轴的转动惯量。
m 解： σ πR 2
dm σ 2π rdr
dJ r dm 2πσ r dr
5
匀变速圆周运动的基本公式
p
1 2 0 0t t 2
0 t
s
R
o

p
x
2 2 0 2 ( 0 )
定轴转动刚体上任一点的速度和加速度 s R 路程与角位移之间的关系：
v R 线速度与角速度的关系：
加速度与角量的关系： 2 dv d v at R R , an 2 R, dt dt R
1
柱壳形状的质元 ,其长为l半径为r厚度为dr, 则该质元的质量为 dm dV ( 2 rdr )l
R2
R2
l
J r dm 2lr dr
2 3 m R1
l
2
刚体定轴转动概述

刚体定轴转动概述


m
已知： m , m1 , m2 , r , 0 0
r
求： t ?
m2
m1
思路：质点平动与刚体定轴转 动关联问题，隔离法，分别列 方程，先求角加速度, 再
23
N
β
r
解：在地面参考系中，分别以 m1 , m2 , m 为研究对象，用隔离法，分别以牛顿第 二定律和转动定律建立方程。 对于 m 1
3 、物理意义：转动惯性的量度 .
I 大 转动惯性大
4、转动惯量的计算
若质量离散分布 若质量连续分布
I＝ mi ri
i
2
I r dm
2
O m2
例：如图m1 ，m2绕OO′转动，
它们距轴的距离分别为
2 1 l l 3 、 3
m1
2 l 3 1 l 3
则，系统的转动惯量为
2 1 I = m1 l m2 l 3 3
dm 2rdr l
l
3
R
O
r
dr
dI r dm 2lr dr
2
I
dI


R
0
m 1 2 I mR R 2l 2
1 4 2lr dr R l 2
3
可见，转动惯量与l无关。所以，实心圆柱对其轴的转动惯量 也是mR2/2。
m1 g T1 m1a1 (1)
T2 m2 g m2 a2 (2)
2
T2 mg
T1
对于 m 2
对于滑轮 m T r T r I 1 mr 2 (3) 1 2
T2
a2
T1
m2 g
思考：
大学物理—刚体的动轴转动

大学物理—刚体的动轴转动


F
（3） F1 对转轴的力矩为零，
在定轴转动中不予考虑。
转动 平面
r
F2
（4）在转轴方向确定后，力对 转轴的力矩方向可用+、-号表示。
2. 刚体定轴转动定律 对刚体中任一质量元mi
O’
f i -内力
-外力
ω
Fi
ri
mi
fi
i i
Fi
应用牛顿第二定律，可得： O
v v r sin r sin 900
和 构成的平面，如 图所示相应的切向加速度和向心加速度分别为
v 的方向垂直于
2
r 78.5m / s
r
at ar 3.14m / s
3
2
2
an r 6.16 10 m / s 边缘上该点的加速度 a an al 其中 a l 的方向 与 v 的方向相反，a n 的方向指向轴心，a 的大小
1 m1 2m 2 m g M / r 2 T1 m1 g a 1 m 2 m1 m 2
22
1 m2 2m1 m g＋M / r 2 T2 m1 g－a 1 m 2 m1 m 2
§4- 1 刚体的平动、转动和定轴转动
1. 刚体 刚体是一种特殊的质点系，无论它在多大外力 作用下，系统内任意两质点间的距离恒保持不变。 2.平动和转动 刚体最简单的运动形式是平动和转动。 当刚体运动时，如果刚体内任何一条给定的直 线，在运动中始终保持平行，这种运动叫平动。 刚体平动时，在任意一段时间内，刚体中各质 点的位移相同。且在任何时刻，各质点的速度和加 速度都相同。
大学物理—刚体的动轴转动

大学物理—刚体的动轴转动


25
麦克斯韦分布
2 1 2 d mgR J mR 3 2 dt
设圆盘经过时间t停止转动，则有
t 0 2 1 g dt R d 0 0 3 2
F1
转动 平面
F
F2
r F1 只能引起轴的
变形, 对转动无贡献。 注 （1）在定轴动问题 中，如不加说明，所指的 力矩是指力在转动平面内 的分力对转轴的力矩。
r
（2） M Z rF2 sin F2d
d r sin 是转轴到力作
用线的距离，称为力臂。
F123麦克来自韦分布例 2: 一半径为 R ，质量为 m 匀质圆盘，平放 在粗糙的水平桌面上。设盘与桌面间摩擦系数为 ，令圆盘最初以角速度 0 绕通过中心且垂直盘 面的轴旋转，问它经过多少时间才停止转动？

d r dr
R
e
解 : 因摩擦力不是集中作用于一点，而是分布 在整个圆盘与桌子的接触面上，力矩的计算要用积 分法。在图中，把圆盘分成许多环形质元，每个质 元的质量dm=rddre，所受到的阻力矩是rdmg 。
a m2 G2
a
21
式中是滑轮的角加速度，a是物体的加速度。滑轮 边缘上的切向加速度和物体的加速度相等，即
麦克斯韦分布
a r
从以上各式即可解得
m 2 m1 g M r / r m 2 m1 g M / r a
J m 2 m1 2 r 1 m 2 m1 m 2
1. 刚体的角动量
图为以角速度绕定轴oz 转动的一根均匀细棒。
L
z

ri
O
Li
把细棒分成许多质点，其中第 i 个质点的质量为 mi 当细棒以转动时，该 质点绕轴的半径为 ri
刚体定轴转动

刚体定轴转动

刚体定轴转动
1.刚体的转动 刚体的转动 在圆盘上任意取一个质元 切向速度： 切向速度：
ω
c
vi = ωri = θri
mi , ri
r i
mi
r ai = ωri = θi = αri 切向加速度： 切向加速度：
角加速度rad
s2
由于质元是任取的，所以刚体上各质元的v 由于质元是任取的，所以刚体上各质元的v、a一般 角加速度α 不同，但角量（角位移θ、角速度ω 、角加速度α）都 不同， 角位移θ 角速度ω 相同，所以描述刚体定轴转动用角量最方便 用角量最方便。 相同，所以描述刚体定轴转动用角量最方便。
刚体定轴 转动定律 对 比 牛顿第二定律
dLc = d (I cω ) = I dω = I α Mc = c c dt dt dt
dp d(mv) dv F= = =m =ma dt dt dt
刚体定轴转动定律在转动问题中的地位相当于质 刚体定轴转动定律在转动问题中的地位相当于质 点运动中牛顿第二定律 牛顿第二定律的 点运动中牛顿第二定律的，各物理量间存在明显的 对应关系。 对应关系。
刚体定轴转动
1
安徽工业大学 数理学院 刘畅
2. 刚体的转动动能和转动惯量 刚体的转动动能 转动动能和 1 2 1 2 2 质元 mi的动能 Eki = mivi = miω ri m i 2 2 r c i 总动能 Ek = ∑Eki 2 1 ω 2 2 2 = ∑ miω ri = ∑miri 2 2 1 I—转动惯量 = Ic ω2 2 单个质点绕定轴转动的转动惯量 单个质点绕定轴转动的转动惯量 I = mr 2 质量连续分布的刚体的转动惯量 I = r dm
dt 若 M =0LΒιβλιοθήκη M =dL∫
2-4 刚体定轴转动的角动量和角动量守恒定律

2-4 刚体定轴转动的角动量和角动量守恒定律

第四章 刚体的定轴转动
9

物理学
第五版
2-4 刚体定轴转动的角动量和角动量守恒定律
例1 一个物体正在绕固定光滑轴自由转动， (A)它受热膨胀或遇冷收缩时，角速度不变 (B)它受热膨胀时角速度变大，遇冷收缩时 角速度变小 (C)它受热膨胀或遇冷收缩时，角速度均变大 (D)它受热膨胀时角速度变小，遇冷收缩时
in
M L 常量
ex
角动量守恒定律是自然界的一个基本定律.
第四章 刚体的定轴转动
7
物理学
第五版
2-4 刚体定轴转动的角动量和角动量守恒定律
许多现象都可 以用角动量守恒来 说明.
花样滑冰 茹可夫斯基凳
m
m
ω
第四章 刚体的定轴转动
r2
r1
8
物理学
第五版

2-4 刚体定轴转动的角动量和角动量守恒定律 直升机螺旋桨的设置
第五版
2-4 刚体定轴转动的角动量和角动量守恒定律
3

刚体定轴转动的角动量定理
质点mi受合力矩Mi(包括Miex、 Miin )
in 合外力矩 M 对定轴转的刚体 i 0 ，
dLi d( J ) d 2 Mi (mi ri ) dt dt dt
ex d d ( J ) 2 M M i ( mi ri ) dt d t d( J ) dL 刚体定轴转动 M dt dt 的角动量定理
第四章 刚体的定轴转动
5

物理学
第五版
2-4 刚体定轴转动的角动量和角动量守恒定律
对定轴转的刚体，受合外力矩M，从 t1到 t 2内，角速度从 ω1变为 ω2，积分可得：
大学物理刚体的定轴转动

大学物理刚体的定轴转动


2l
l
17
例 一匀质细杆，长为 l 质量为 m ，在摩擦系数为
的水平桌面上转动，求摩擦力的力矩 M阻。 解： 建立如图坐标，取质元
dm dx
质元受阻力矩：
dM 阻 dmgx
o
xl dm m dx
x
细杆受的阻力矩
M阻
dM
阻
0l
gxdx
1 mgl
2
18
例 一半径为R，质量为m的均匀圆盘平放在粗糙的
令 J miri2
刚体绕Z轴转动的转动惯量
即
M z J ----刚体的定轴转动定律
说明
1. 上式是矢量式（力矩只有两个方向）。
2. M、J、是对同一轴而言的。
3. 具有瞬时性，是力矩的瞬时效应。
4. 转动惯量J是刚体转动惯性大小的量度。
8 8
3、转动惯量的计算
转动惯量： J miri2
l
r
dr
d
dm g
M
dM
l
0
mg l
r
cosdr
mg
l 2
cos
16
M J 1 ml2
3
3g cos
2l
(2) d d d d 3g cos dt d dt d 2l
分离变量积分 g cos d l d
02
03
(3g sin ) l
300 , 3g 900 , 3g
i
质量连续分布的刚体： J r2dm
质量为线分布： dm dl
面分布： dm ds
体分布： dm dV
1）总质量
转动惯量与下列因素有关： 2）质量分布 3）转轴位置
9
✓ J与质量分布有关：
大学物理4-2刚体的角动量 转动动能 转动惯量

大学物理4-2刚体的角动量 转动动能 转动惯量

J ri2mi r2dm
刚体绕定轴的角动量表达式：
Lz J
刚体的转动动能
2. 刚体的转动动能
刚体的转动动能应该是组成刚体的各个质点
的动能之设和刚。体中第i个质点的质量为 ， mi
速度为 v,i 则该质点的动能为：
1 2
mivi2
刚体做定轴转动时，各质点的角速度相同。
设质点
mi
离轴的垂直距离为
vi ri
ri ，则它的线速度
因此整个刚体的动能
EK
12mivi2
1 2
ri2mi 2
刚体的转动动能
式中 式写为
是m刚iri体2 对转轴的转动惯量
EK
1 2
J 2
，所J以上
上式中的动能是刚体因转动而具有的动能，因 此叫刚体的转动动能。
转动惯量的计算
3. 转动惯量的计算
按转动惯量的定义： J ri2mi
刚体的质量可认为是连续分布的，所以上式可 写成积分形式
J r2dm 要求: 细棒、薄圆盘、圆环
dl 其中质元dm可表示为 dm ds
dv
r —为质元到转轴的距离
转动惯量的计算
刚体运动：
平动： 平动动能 1 mv2 线动量 mv
2
定轴转动：转动动能 1 J 2 角动量 J
2
质量是刚体平动时惯性大小的量度。 转动惯量是刚体转动时惯性大小的量度。 补：平行轴定理、垂直轴定理（适用于薄平面刚体）。
Li Ri pi Ri mivi
因 vi Ri ，所以 L的i 大小为
Li mi Rivi
方向如图所示。
z
L
Li Liz
ri
O Ri mi
刚体的角动量
[分享]第四章刚体的转动问题与习题解答

[分享]第四章刚体的转动问题与习题解答

第四章 刚体的转动 问题与习题解答问题：4-2、4-5、4-94-2如果一个刚体所受合外力为零，其合力矩是否也一定为零？如果刚体所受合外力矩为零，其合外力是否也一定为零？答：一个刚体所受合外力为零，其合力矩不一定为零，如图a 所示。

刚体所受合外力矩为零，其合外力不一定为零，例如图b 所示情形。

4-5为什么质点系动能的改变不仅与外力有关，而且也与内力有关，而刚体绕定轴转动动能的改变只与外力矩有关，而与内力矩无关？答：因为合外力对质点所作的功，等于质点动能的增量；而质点系中内力一般也做功，故内力对质点系的动能的增量有贡献。

而在刚体作定轴转动时，任何一对内力对转轴的力矩皆为一对大小相等、方向相反的力矩，且因定轴转动时刚体转过的角度d θ都一样，故其一对内力矩所作的功()0inij ij ji ij ji W M d M d M M d θθθ=+=+=，其内力功总和也为零，因而根据刚体定轴转动的动能定理可知：内力矩对其转动动能的增量无贡献。

4-9一人坐在角速度为0ω的转台上，手持一个旋转的飞轮，其转轴垂直地面，角速度为ω'。

如果突然使飞轮的转轴倒转，将会发生什么情况？设转台和人的转动惯量为J ，飞轮的转动惯量为J '。

答：（假设人坐在转台中央，且飞轮的转轴与转台的转轴重合）视转台、人和飞轮为同一系统。

（1）如开始时飞轮的转向与转台相同，则系统相对于中心轴的角动量为：10L J J ωω''=+飞轮转轴快速倒转后，飞轮的角速度大小还是ω'，但方向与原来相反；如设转台此时的角速度为1ω，则系统的角动量为：21L J J ωω''=-在以上过程中，外力矩为零，系统的角动量守恒，所以有：10J J J J ωωωω''''-=+即 102J Jωωω''=+，转台的转速变大了。

（2）如开始时飞轮的转向与转台相反，则系统相对于中心轴的角动量为：10L J J ωω''=-飞轮转轴快速倒转后，飞轮的角速度大小还是ω'，但方向与原来相反；如设转台此时的角速度为1ω，则系统的F 1F 3ab角动量为：21L J J ωω''=+在以上过程中，外力矩为零，系统的角动量守恒，所以有：10J J J J ωωωω''''+=-即 102J Jωωω''=-，转台的转速变慢了。

刚体的定轴转动

半径为R、质量为 m3的均质圆盘，忽略轴 的摩擦。求：(1) m1 、m2的加速度；(2)滑 轮的角加速度 及绳中的张力。（绳轻且
不可伸长）
R m3
m1
m2
24
R
m1
m2
解 对m1 、m2，滑轮作受力分析， m1 、 m2作平动，滑轮作转动，
(T1 T1，T2 T2)
m1g T1 m1a
T2 m2 g m2a
其一 此处滑轮质量不可忽略，大小不可忽略，所以要用到转动定律；
其二 绳与滑轮间无相对滑动，所以
；因a R
故滑轮两边绳之张力不相等。
26
例2－33 质量m=1.0kg、半径 r=0.6m 的匀质圆盘，可以绕通过其中心且垂直盘面的水
平光滑固定轴转动，对轴的转动惯量 I=mr2/2。圆盘边缘绕有绳子，绳子下端挂一质量
质量分布均匀而有一定几何形 状的刚体，质心的位置为它的 几何中心。
X
32
五、机械能守恒定律 若 A外 0 A内非 ＝０ (或只有保守力作功)
系统机械能守恒，即
1 2
mv2
1 2
I2
mghc
1 2
k x2
恒量
33
例2－35 一均匀细杆长为l，质量为m，垂直放置，o点着地。杆绕过o的光滑水平轴
m=1.0kg 的物体，如图所示。起初在圆盘上加一恒力矩使物体以速率 v0=0.6m/s 匀速上 升，如撤去所加力矩，问经历多少时间圆盘开始作反方向运动？
r
T
m、r
T
a
v0
mg
解；受力分析如图所示
mg T ma
Tr I
a r
v0 at 0
I 1 mr2 2
解得 a mgr mr I r 2g 3

4-2力矩转动定律转动惯量


J r2dm
图1
图2
J1 J2
➢ 常用的转动惯量 （P110 表）
21
四 平行轴定理
质量为m 的刚体，
如果对其质心轴的转动 惯量为 JC ，则对任一与
该轴平行，相距为 d 的
转轴的转动惯量
JO JC md 2
d
C mO
J Jc
22
J Jc md2
圆盘对P 轴的转动惯量 P R O m
Fit Fit miait miri
11
➢ 质元绕Z轴转动的力矩
M i ri Fit ri Fit miri2
➢ 刚体绕Z轴转动的力矩
z
Fi内
Fi外
r O i m i 质量元
Mi riFit riFit
mi ri 2
M

r
F
M Frsin Fd
5
4、一对力偶的力矩
M Fd

F
F
o
l


F 0 M 0
M F l F l Fl
22
ro
F'
F

F 0

M 0
M Fr Fr 0
6
讨论
（1）若力 F不在转动平面内，把力分
解为平行和垂直于转轴方向的两个分量
41
➢ 常用的转动惯量公式
m质点：J r2m 圆盘(圆柱): J 1 mR2
2
杆：
Jc

1 12
mL2
J
端

1 3
mL2
R Om
O1
O1’
d=L/2

刚体定轴转动定律

于 180°的夹角 θ 转向 F 时，拇指所指的方向就是力矩的方向。
可见，力矩的方向与转轴的方向平行，只有两个可能的方向，因此，可用 M 的正负表示力矩的方向。 一般可按力矩的作用来判断其正负：由转轴 Oz 正向俯视，若力矩的作用使刚体逆时针转动，则力矩为 正，否则为负。
刚体定轴转动定律 1.1 力矩
可加性
• 对同一转轴而言，刚体各部分转动惯量之 和等于整个刚体的转动惯量。
平行轴定理
• 设有两个彼此平行的转轴，一个通过刚体 的质心，另一个不通过质心。两平行轴之 间的距离为d，刚体的质量为m。
如果此刚体对通过质心转轴的转动惯量为 Jc ，则对另一 转轴的转动惯量 J 为 J Jc md 2
刚体定轴转动定律
刚体定轴转动定律Βιβλιοθήκη ， ，，，
例题讲解 2
如图所示，一轻绳跨过一轴承光滑的定滑轮。绳两边分别悬有质量为 m1 和 m2 的两个物体 A，B。已知 m1
小于 m2 ，滑轮可看作质量均匀分布的等厚圆盘，其质量为 m，半径为 r，设绳与滑轮间无相对滑动。求：① 物
体的加速度；② 滑轮的角加速度；③ 绳的张力。
i 1
n
用 M 表示，即 M (Δmiri2 ) β
i 1
n
n
式中的 (Δmiri2 ) 称为转动惯量，用 J 表示，即 J (Δmiri2 )
i 1
i 1
于是，式可写为 M Jβ
刚体定轴转动定律 1.2 转动定律
转动定律：刚体定轴转动时，刚体的角加速度与刚体所受的合外力矩成正比，与刚体的转动惯量 成反比。
r 2 dm
Ω
式中 r ——质元 dm 到转轴的距离（m）。 在国际单位制中，转动惯量的单位为 kg m2 。

转动定律

T
N r
(1) (2) (3) (4) (5)
m1 g
m2g
T'
由(2)、（5）式:
T T J / r
(4)
代入(1)式:
m1 g J / r m1a m1r
2013-3-7
m1 gr m1 gr 2m1 g 2 m1r J m r 2 1 m r 2 (2m1 m2 )r 1 2 2
例3 如图：一定滑轮两端分别悬挂质量都是 m的物块A和B，图中R和r，已知滑轮的转动 惯量为J，求A、B两物体的加速度及滑轮的 角加速度。
解：建立转动轴的正方 向—垂直于纸面向内为正。 隔离物体分析力：

T1
r
R
T2
a1 T1
A
T2
B
mg
2013-3-7
a2 mg
15
由
mg T2 ma2 T mg ma 1 1 T2 R T1r J a r 1 a2 R
m


2013-3-7
3
解 ：设圆盘面密度为 ，在盘 上取半径为 r ，宽为 dr 的圆 环。
例 2 一质量为 m 、半径为 R的均匀圆盘，求通过盘 中心 O 并与盘面垂直的轴的转动惯量 。
圆环质量： dm 2 rdr
圆环对轴的转动惯量：
2 3
RR
O
r dr
m dJ r dm 2 r dr 而 2 πR R 1 3 4 2 J 2 π r dr π R mR 0 2 2
2013-3-7 18
解：细杆受重力和 铰链对细杆的约束力 FN 作用，由转动定律得
m,l F N θ

(完整版)转动定律讲解

d力臂:转轴到力作用线的垂直距离
方向: r F 的方向 单位: N m
对于定轴转动；
z
M
r
Od
F
P*
规定转动正方向,力矩使刚体绕
正方向转动, M 取正,反之取负。
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
讨论 1）与转轴平行的力对转轴不产生力矩;
2）与转 轴垂直但通过转轴的力对转轴不产生力矩； 3）若力 F 不在转动平面内，把力分解为平行和垂
直于转轴方 向的两个分 量 F Fz F
其中 Fz 对转轴的力
矩为零，故 F 对转轴的
力矩
M r F
M z rF sin
4）合 力矩 等于各分力矩的矢量和
M M1 M2 M3
第四章 刚体的定轴转动
z
k
Fz
F
O r
F
定轴转动：（规定转动 正方向）
M Mi
i
4 – 2 力矩 转动定律 转动惯量
力矩可以反映力的作用点的位置对物体运动的影响.
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
一 力矩
刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P ,
r 且在转动平面内, 为由点O 到力的作用点 P 的径
矢 .
F 对转轴 Z 的力矩 M rF
M
力矩是矢量
大小: M Frsin Fd
M i Fitri (mi )atri
at ri
Mi (mi )ri2
z
Fit
O
ri
mi
M Mi (mi )ri2 (mi )ri2
➢ 转动惯量

大学物理 第四章 刚体的转动 4-2 力矩 转动定律 转动惯量


} ⇒ω
} ⇒θ
2、 M = Jα
F = ma
}⇒
17
m反映质点的平动惯性，J 反映刚体的转动惯性。 反映质点的平动惯性， 反映刚体的转动惯性。 反映质点的平动惯性
三 转动惯量
J 的计算方法 质量离散分布
J = ∑ ∆m r
j
2 j j
J = ∑ ∆m r = (∆m )r + (∆m2 )r + L+ (∆mN )r
质量为m，长为L的细棒绕其一端的 的细棒绕其一端的J 质量为 ，长为 的细棒绕其一端的
1 2 J c = mL 12
O1
O1’
L2 1 2 J = J c + m( ) = mL 2 3
d=L/2
O2 O2’
20
竿 子 长 些 还 是 短 些 较 安 全 ？
飞轮的质量为什么 大都分布于外轮缘？ 大都分布于外轮缘？
（3） ）
1 2 对M： T2 r − T1r = J α = M r α ： 2
4、运动学： 运动学：
rα = a
（4） ）
26
解以上四个联立方程式, 解以上四个联立方程式 可得
1 T2 ' ≠ T 、
原因： 原因：
' 1
' (1)若：T2 ' = T T2 ' r −T ' r = Jα v 1 1 FN v 1 T 1 ⇒ J = mr2 = 0 ⇒m = 0 2 m
21
例1（补充例题）：一个转动惯量为2.5 kg⋅m2 、 （补充例题） 一个转动惯量为 ⋅ 例题 直径为60cm 的飞轮，正以 的飞轮，正以130 rad⋅s−1 的角速度旋转。 直径为 ⋅ 的角速度旋转。 现用闸瓦将其制动, 现用闸瓦将其制动 如果闸瓦对飞轮的正压力为 500 N, 闸瓦与飞轮之间的摩擦系数为0.50。求： 闸瓦与飞轮之间的摩擦系数为 。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章 刚体的转动
2
大学 物理学
4-1 刚体定轴转动的描述 （1）角速度是矢量 角速度矢量的方向 沿转轴方向
3. 角速度和角加速度的矢量性

转动 方向
在刚体绕固定轴转动的情况下， 角速度的方向只有两种可能的 取向，这时就可把角速度看成 右手螺旋定则确 代数量，正负号就可表示其两 定角速度的方向 种取向。
(3) 电动机转动的角加速度为
d m t / e 540 πe t / 2 rad s 2 dt
第四章 刚体的转动
10
大学 物理学
4-1 刚体定轴转动的描述
例2 在高速旋转圆柱形转子可绕垂直 其横截面通过中心的轴转动．开始时，它的 角速度 ω0 0 ，经300 s 后，其转速达到 18 000 r· min-1 ．转子的角加速度与时间成正 比．问在这段时间内，转子转过多少转？ 解
d d 2 dt dt
2
9
第四章 刚体的转动
大学 物理学
4-1 刚体定轴转动的描述
解 (1) 将 t=6 s 代入 ω m (1 e
t /
)
ω 0.95ωm 513r s
1
(2) 电动机在6 s内转过的圈数为
1 6 1 6 t / N ωdt ωm (1 e )dt 2π 0 2π 0 3 2.2110 r
4-1 刚体定轴转动的描述 2. 描述刚体定轴转动的物理学量:
由于刚体中任意质点的位置
一定,则刚体中所有质点的位
z
ω。
O
r P’(.t+dt)
.
x
由于刚体中所有质点的Δθ、ω和相同，所以可
以用任意一质点的Δθ、ω和来描述刚体的转动
角度、转动快慢和转动变化的快慢。 所以，把任意一个质点的Δθ、ω和叫做刚体的 Δθ、ω和 ；Δθ、ω和属于刚体
在 300 s 内转子转过的转数
π 3 4 N (300 ) 3 10 2π 2π 450
第四章 刚体的转动
13

d 令 ct，即 ct ，积分 dt 1 2 t 得 ct d c t d t 0 0 2
第四章 刚体的转动
11
d d 2 2 dt dt
大学 物理学
4-1 刚体定轴转动的描述
1 2 ct 2
当 t =300 s 时
18 000 r min 600π rad s
第四章 刚体的转动
8
大学 物理学
4-1 刚体定轴转动的描述
模型：刚体定轴转动 已知： 当t 0时， 0 启动后：
m (1 e
1
t /
)
m 540 r s ， 2.0 s
求： (1)当t 6s时，6 ?
(2)从t 0到t 6s，转动圈数 N（ ？） (3) t
1
1
2 2 600 π π 3 c 2 rad s 2 t 300 75 1 2 π 2 ct t 2 150
第四章 刚体的转动
12
大学 物理学
4-1 刚体定轴转动的描述
d π 2 t 由 dt 150 π t 2 t dt 得 d 0 150 0 π 3 t rad 450
a


加速
减速
大学 物理学
4-1 刚体定轴转动的描述
二 匀变速转动公式
当刚体绕定轴转动的 =常量时，刚体 做匀变速转动．
dv d x 2 dt dt
质点匀变速直线运动
2
d d 2 dt dt
2
刚体绕定轴作匀变速转动
x x0 v0t at 0 0t t 2 2 2 2 v v0 2a( x x0 ) 0 2 ( 0 )
第四章 刚体的转动
3
大学 物理学
4-1 刚体定轴转动的描述 线速度与角速度之间的关系 因v = r ，同时，由式中三 者方向之间的关系，可得
v r

dt
（2）角加速度矢量 矢量式 d
d dt
因角速度矢量的方向沿转轴方向，所以角加速 度的方向亦沿转轴方向
第四章 刚体的转动
2
2 a ret rω en
7
第四章 刚体的转动
大学 物理学
4-1 刚体定轴转动的描述
例1 在高速旋转的微型电动机里，有一 圆柱形转子可绕垂直其横截面并通过中心的 转轴旋转．开始起动时，角速度为零．起动 t / 后其转速随时间变化关系为： m (1 e ) 式中 m 540 r s1， 2.0 s ．求： (1)t=6 s时电动机的转速．(2)起动后，电动 机在 t=6 s时间内转过的圈数．(3)角加速度 随时间变化的规律．
4
大学 物理学
4-1 刚体定轴转动的描述 和匀变速直线运动比较，得：
、 同向，刚体做加速转动；反之，做减速转动
刚体做定轴转动时， 在实际运用中一般按 如下规定： 角速度矢量都为正 当角加速度矢量为正时， 表示刚体做加速转动； 当角加速度矢量为负时， 表示刚体做减速转动。
第四章 刚体的转动
5
a
1 2 2
1 2 2
第四章 刚体的转动
6
v v0 at
0 t
大学 物理学
4-1 刚体定轴转动的描述
三 角量与线量的关系 d ω dt 2 dω d 2 dt dt v rωet

an

a r
et v a
t
at r an rω
大学 物理学
一
刚体转动的角速度和角加速度
1. 描述刚体转动的物理学量:
4-1 刚体定轴转动的描述
怎样描述？ 运动学
质元运动: 圆周运动 描述质元运动的物理学量:
角坐标 (t ) 角位移
y
d 角速度 dt d 角加速度 dt
第四章 刚体的转动
B
r
o

A

x
1
参考方向
大学 物理学