1描写刚体定轴转动的物理量(大学物理 - 刚体部分)

T2
( 2 m1 m / 2 ) m 2 g m 2 M f / R m1 m 2 m / 2
例4.如图所示长度不等的A ,B两个匀质细棒(材料粗细均相 同), 从竖直位置由静止开始自由倒向地面,问:A B棒哪根先倒地?
M rF
M mg l 2 sin( )
三. 转动惯量
I
m
i 1
n
r i i
2
是刚体转动惯性大小的量度 (质量是物体惯性大小的量度) 1. 刚体的质量 由三个因素决定: 2. 质量的分布 3. 转轴的位置
物理意义:
M I
2 如果刚体是连续分布的质点系 I r d m 单位：kg m2
质量为体分布: d m d V 质量为面分布: d m d s
dm m l d x
1 2
1
l
I I
r

2
dm
O
dm
x
l
2
x dm
I
1 l
2

2 1 l 2
m l

l
m l
x dx
2
0

1 3
ml
2
x d x
l 2
2
z l
ml
2

3 mx l 3

l 2
1 12
o
dx
x
例2: 计算质量为m, 半径为R的均匀细圆环的转动惯量. 轴与圆环平面垂直并通过圆心。 解: 如图各质元到轴的垂直距离相等 m
质点角动量 L r p r m v
刚体的角动量(定轴转动)
L I

⑶ t =6 ·0 s 时转过的角度为
6s
0
6s
d t 0
0(1et)dt
0 [te t]6 0 s 9 [6 ( 2 0 0) 5 (0 2 )]369rad
则 t =6 ·0 s
时电动机转过的圈数
N 587圈 2
5.2 5.4 刚体的转动定律及应用
5.2.1力对转轴的力矩
转轴
§5.1 刚体的运动的描述 §5.2 刚体定轴转动 §5.3 转动惯量的计算 §5.4 转动定律应用 §5.5 角动量守恒 §5.6 定轴转动中的功和能
5.1 刚体的运动的描述
•刚体（rigid body）
任何情况下形状和体积都不改变的物体(理想化模型)。 刚体是特殊的质点系。 刚体可以看作是由许多质点组成,每一个质点叫做 刚体的一个质元,刚体这个质点系的特点是,在外 力作用下各质元之间的相对位置保持不变。
2、刚体定轴转动的转动定律
M d(J )dL J
dt dt
刚体绕定轴转动时，它的角加速度与作用于刚体上的 合外力矩成正比，与刚体对转轴的转动惯量成反比。
刚体定轴转动的转动定律
M＝J 与 F ma地位相当 m反映质点的平动惯性，J 反映刚体的转动惯性
力矩是使刚体转动状态发生改变而产生角加速度的原因。力
ri
即 F itfitΔ m iri
则刚体转动定律为
变形有 F ir tifir tiΔm iri2
M J
对所有质元求和:
F ir ti fir ti (m ir i2 ) 上式表明:
这里 FitriM i M外
刚体绕定轴转动时,刚
fitri 0 定义 JΔmiri2 叫转动惯量
体的角加速度与它所 受的合外力矩成正比.

第二节 转动惯量
1
一、转动惯量 刚体的动能等于各 质点动能之和。
2
刚体的动能 与平动动能比较
相当于描写转动惯性的物理量 转动惯量的定义： 单位： 千克 ·米2
3
§4.刚体的转动惯量/ 一、转动惯量
转动惯量
4
§4.刚体的转动惯量/ 二、转动惯量的计算
刚体的转动惯量与哪些物理量有关？ ①.与刚体质量有关。 ②.与质量对轴的分布有关。 ③.与轴的位置有关。
细棒转轴通过中 心与棒垂直
l
细棒转轴通过端 点与棒垂直
14
§4.刚体的转动惯量\ 三、典型刚体的转动惯量
2r
2r
球体转轴沿直径
球壳转轴沿直径
15
§4.刚体的转动惯量/ 三、典型刚体的转动惯量
四、平行轴定理 定理表述： 刚体绕平行于质心轴的转动惯 量 J，等于绕质心轴的转动惯量 JC 加上刚 体质量与两轴间的距离平方的乘积。
二.质量连续分布刚体的转动惯量计算
1.计算公式
5
§轻杆的 b 处 3b 处各系质量 为 2m和 m 的质点，可绕 o 轴转动，求： 质点系的转动惯量J。 解： 由转动惯量的定义
6
§4.刚体的转动惯量\ 二、转动惯量的计算
例2：长为 l、质量为 m 的匀质细杆，绕与 杆垂直的质心轴转动，求转动惯量 J。
建立坐标系，坐标原点选在边缘处。分 割质量元 dm ,长度为 dx ,
9
§4.刚体的转动惯量/ 二、转动惯量的计算
10
§4.刚体的转动惯量/ 二、转动惯量的计算
例4：半径为 R 质量为 M 的圆环，绕垂直 于圆环平面的质心轴转动，求转动惯量J。 解： 分割质量元 dm 圆环上各质量元到 轴的距离相等，

13
【例5】长为 l、质量为 m 的匀质细杆，绕与杆垂直的 质心轴转动，求转动惯量 J。
【解】建立坐标系，分割质量元
J x2dm

l2 l 2
x2Байду номын сангаас
ml dx
1 ml 2 12
x o x dx
【例6】长为 l、质量为 m 的匀质细杆，绕细杆一端轴 转动，求转动惯量 J。
【解】J x2dm
L
L
11
【例2】半径为 R 质量为 M 的圆环，绕垂直于圆环平 面的质心轴转动，求转动惯量J。
【解】分割质量元，环上各质元到轴的距离相等。
M
J
R2dm R2
M
dm
MR2
0
0
【例3】在无质轻杆的 b 处 3b 处各系质量为 2m 和 m 的质点，可绕 O轴转动，求质点系的转动惯量J。
刚体作定轴转动时, 刚体上各质点都作圆周运动。 各质点运动的线量一般不同，但角量完全相同。
1.角坐标
OP与极轴之间的夹角称 为角坐标（或角位置）
角坐标为标量，但可有正负。
o
P

x
在定轴转动过程中，角坐标是时间的函数： =(t)，称为转动方程。
3
2.角位移
角坐标的增量 称为刚体的角位移
i
i
i
得 LJ

v i m i ri
29
由刚体定轴转动定律
得到
MJ J
d dt
d( J ) dt

dL dt
M dL 定轴转动刚体角动量定理微分形式 dt
t
L
Mdt d
t0
L0
LLL0

dm ds dm dV
面密度和体密度。
线分布
面分布
体分布
注 意
只有对于几何形状规则、质量连续且均匀分布
的刚体，才能用积分计算出刚体的转动惯量。
[例3.1]: 求长为L、质量为m的均匀细棒对图中不同 轴的转动惯量。 [分析]：取如图坐标，dm=dx
A B
L
X
J A r dm
2
x dx mL / 3
T1 mg sin ma 1 2 T2 R T1 R J mR 2 mg T2 ma
a R
mg
[例3.4]: 转动着的飞轮的转动惯量为J，在t=0时角速度 为ω0。此后飞轮经历制动过程，阻力矩M的大小与角速度 ω的平方成正比，比例系数为k（k>0）,当ω= ω0/3时，飞 轮的角速度及从开始制动到现在的时间分别是多少？ [分析]: (1)已知 M k 2
练习：右图所示，刚体对经过
棒端且与棒垂直的轴的转动惯
mL
量如何计算？(棒长为L、球
半径为R）
mO
J L1
1 2 mL L 3
2 2 J o mo R 5
2 2
J L 2 J 0 m0 d J 0 m0 ( L R)
1 2 2 2 2 J mL L mo R mo ( L R) 3 5
dL d ( mv ) dr d (mv ) dr r mv F , v dt dt dt dt dt dL v mv 0, r F M r F v mv dt dL 角动量定理的微分形式 M dt
平均角速度
角速度
t

mg FT2 ma2

FT1 FT2
R
mg FT1 r
m
a1
J
a1 r
a2 R
FT1 r R
FT1'
A
mg
β
FT2
FT2'
B
mg
mg(R r)
J mR2 mr2
a1

r

J
mgr(R r) mR2 mr2
40 半径减小角速度增加。
（2）拉力作功。请考虑合外力矩为0， 为什么拉力还作功呢？
W


0
Md
在定义力矩作功 时，我们认为只 有切向力作功， 而法向力与位移 垂直不作功。
但在例题中，小 球受的拉力与位 移并不垂直，小 球的运动轨迹为 螺旋线，法向力 要作功。
o
F
r d Fn F
解得
a2

R

mgR(R r) J mR2 mr2
FT1 mg ma1
FT2 mg ma2
例2：光滑斜面倾角为 ，顶端固定一半 径为 R ，质量为 M 的定滑轮，质量为 m 的物体用一轻绳缠在定滑轮上沿斜面 下滑，求:下滑的加速度 a 。
解：物体系中先以
物体 m 研究对象，
A
分别根据牛二定律和转动定律列方程：
角量、线量关系式
解得：
a
mB g
mA mB mC 2
T1

mAmB g
mA mB mC
2
T2

(mA mC 2)mBg mA mB mC 2
如令 mC 0，可得：

第五章 刚体的定轴转动
5.1刚体运动的描述
一.刚体
刚体：在外力作用下，形状和大小都不发生变 化的物体 . （任意两质点间距离保持不变的特殊质点 组）
（1）刚体的运动
刚体的运动形式：平动、转动 .
平动：若刚体中所有点 的运动轨迹都保持完全相同， 或者说刚体内任意两点间的 连线总是平行于它们的初始 位置间的连线 .
F F11 F
其中F11对转轴的力 矩为零，故 F 对转轴的力矩
M zk r F
z
k F11
F
O r
F
M z rF sin
2）合力矩等于各分 力矩的 矢量和 M M1 M2 M3
第五章 刚体的定轴转动
3） 刚体内作用力和反作用力的力矩互相抵消
M ij
O
rj
d ri
i
j
Fji Fij
M
rdf
l
grdr
0
1 gl 2
2
1 mgl
2
dm dl
dm ds
dm dV
其中、、分别
为质量的线密度、 面密度和体密度。
线分布
面分布
体分布
第五章 刚体的定轴转动
m 例1 一质量为 、长为 l 的均匀细长棒，求通过棒中
心并与棒垂直的轴的转动惯量 .
O
Or
l 2 O´ dr l 2
O´ dr l
r 解 设棒的线密度为 ，取一距离转轴 OO´ 为 处的质
fi
第五章 刚体的定轴转动
M i外 M i内 miri2
i
i
i
Mi内 0
i
M i外 ( miri2 )
i
i
z
O rj

2l
l
17
例 一匀质细杆，长为 l 质量为 m ，在摩擦系数为
的水平桌面上转动，求摩擦力的力矩 M阻。 解： 建立如图坐标，取质元
dm dx
质元受阻力矩：
dM 阻 dmgx
o
xl dm m dx
x
细杆受的阻力矩
M阻
dM
阻
0l
gxdx
1 mgl
2
18
例 一半径为R，质量为m的均匀圆盘平放在粗糙的
令 J miri2
刚体绕Z轴转动的转动惯量
即
M z J ----刚体的定轴转动定律
说明
1. 上式是矢量式（力矩只有两个方向）。
2. M、J、是对同一轴而言的。
3. 具有瞬时性，是力矩的瞬时效应。
4. 转动惯量J是刚体转动惯性大小的量度。
8 8
3、转动惯量的计算
转动惯量： J miri2
l
r
dr
d
dm g
M
dM
l
0
mg l
r
cosdr
mg
l 2
cos
16
M J 1 ml2
3
3g cos
2l
(2) d d d d 3g cos dt d dt d 2l
分离变量积分 g cos d l d
02
03
(3g sin ) l
300 , 3g 900 , 3g
i
质量连续分布的刚体： J r2dm
质量为线分布： dm dl
面分布： dm ds
体分布： dm dV
1）总质量
转动惯量与下列因素有关： 2）质量分布 3）转轴位置
9
✓ J与质量分布有关：

M J
p mivi
角动量
L J
角动量定理 M d(J)
dt
质点的运动规律与刚体的定轴转动规律的比较（续）
质点的运动
动量守恒 力的功 动能
Fi 0时
mivi 恒量
Aab
b
F
dr
a
Ek
1 2
mv
2
动能定理
A
1 2
mv
2 2
1 2
mv12
重力势能
Ep mgh
机械能守恒
A外 A非保内 0时
进动特性的技术应用
翻转
外力
C
外力
进动
C
炮弹飞行姿态的控制：炮弹在飞行时，空气阻力对炮弹质心 的力矩会使炮弹在空中翻转；若在炮筒内壁上刻出了螺旋线 （称之为来复线），当炮弹由于发射药的爆炸所产生的强大 推力推出炮筒时，炮弹还同时绕自己的对称轴高速旋转。由 于这种自转作用，它在飞行过程中受到的空气阻力将不能使 它翻转，而只能使它绕着质心前进的方向进动。
pA pB
pA A
Bp B
s
s
O
x
结论：静止流体中任意两等高点的压强相等，即压强差为零。 若整个流体沿水平方向加速运动？ 加速运动为a，压强差为？
2. 高度相差为 h 的两点的压强差（不可压缩的流体）
选取研究对象，受力分析：（侧面？）
沿 y 方向：
p C
Y C s
pB s pC s mg may
已知：p0=1.013×105 Pa ， 0 1.29kg / m3
解 由等温气压公式
p
p e(0g / p0 ) y 0
0g 1.25104 m1
p0
p1 1.0 105 e1.251043.6103 0.64 105 Pa

M f k 2
(1)
由刚体定轴转动定律得：
k2 J J d
(2)
dt
对上式分离变量并积分得：
0
k
J
t
dt
0
2 0
d 2
(3)
得到所需时间为： t J
(4)
k0
（2）由刚体定轴转动定律得：
k2 J J d d J d
(5)
dt d d
0
对上式分离变量并积分得： k
d
2
设 为两飞轮啮合后共同角速度：
J AA 33.3rad s1
JA JB
例题4.3.2 质量 M 、半径 R 的圆盘，绕过圆心 O
且垂直于盘面的水平光滑固定轴转动，已知其角速
惯量，故该量有关于刚体，还有关于转轴！ 2.由上述结果看出：
JO
1 3
ml 2
1 12
ml2 +m（ l ）2 2
JO
+m（ l ）2 2
4.2.3 平行轴定理
平行轴定理：质量为 m的刚体，如果
对其质心轴的转动惯量为 JC ，则对任
一与该轴平行，相距为 d 的转轴的转
动惯量为：
J O J C md 2
2.合力矩等于各分力矩的矢量和 ：
M M1 M2 M3
(2)
3.刚体内力矩互相抵消：
M ij M ji
注意：内力矩对刚体 动力学效应无贡献；
M ij
o
rj
d ri
i
j
Fji Fij
M ji
例题4.2.1 研磨专用动力卡盘是专门为精密研磨 机所设计，如图所示用于固定被加工工件，卡盘在 绕垂直通过盘心的轴转动时会与接触工件产生滑动 摩擦。试求卡盘转动时受到的摩擦力矩。设其质

M

r
F
I z dmiri2
当刚体质量连续分布 I r2dm
组合体的转动惯量 I I1 I2 I3 ... Ii
3 .刚体的定轴转动定律
4. 力矩的功 转动动能
d
M I I
dt
A
2 1
M
Z
d
EK


i
(
1 2
mi
vi2
)

1 I2 2
刚体定轴转动动能定理
A

2
1
M
Z
d

1 2
I22

1 2
I12

EK
机械能守恒定律:只有重力做功时
1 2
I2
m ghC
常量
5. 角动量和冲量矩
刚体的角动量 LZ I
恒力矩的冲量 MZ t
变力矩的冲量
t2 t1
M
Z
dt
6. 角动量定理和角动量守恒定律
A Fdx
EK

1 mv2 2
mv
角位移

角速度 d
角加速度

dt
d
dt
d 2
dt 2
转动惯量J miri2
功
A
2 1
M
Z
d
转动动能
EK

1 J 2
2
角动量
J
功率
P Fv
角功率 P M
课堂讨论题
1.当两个力作用在一个有固定转轴的刚体上下列说法正确吗?
(1)这两个力都平行于轴作用时它们对轴的合力矩一定为零;

刚体如果研究物体的转动就必定涉及物体的空间方位，此时，质点模型已不适用，因为一个点是无方位可言的。

若在所研究的问题中，物体的微小形变可以忽略不计时，则可以引入刚体模型。

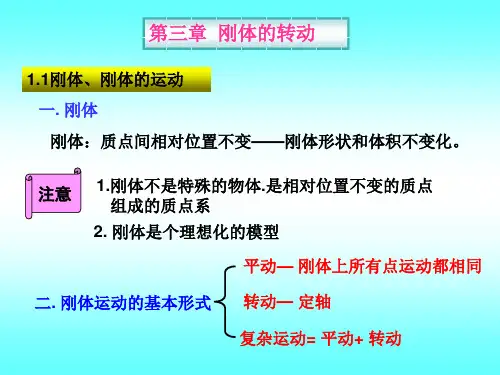
刚体，是指在任何情况下，都没有形变的物体。

也可以把刚体看作一个各质元之间无相对位置变化且质量连续分布的特殊质点系。

（附图）刚体定轴转动的描述在物体运动过程中，如果物体上的所有质元都绕某同一直线作圆周运动，这种运动就称之为转动，这条直线称为转轴 (这根轴可以在物体之内，也可以在物体之外的某固定处)。

若转轴的方向或位置在物体运动过程中变化，这个轴在某个时刻的位置便称为该时刻的转动瞬轴。

若转动轴固定不动，即既不改变方向又不平移，则这个转轴称为固定轴，这种转动称为定轴转动。

（附图）平动和转动是刚体运动中两种基本形式．无论刚体作多么复杂的运动，总可以把它看成是平动和转动的合成运动。

例如一个车轮的滚动可以分解为车轮随着车轴的平动和整个车轮绕着车轴的转动。

定轴转动是刚体运动中最简单的运动形式之一。

为了研究刚体的定轴转动，定义：垂直于固定轴的平面为转动平面。

研究刚体的定轴转动时，可以任取一个转动平面来讨论。

以转轴与转动平面的交点为原点，则该转动平面上的所有质元都绕着这个原点作圆周运动。

在转动平面内过原点作一射线作为参考方向(或称极轴)，转动平面上任一质元P 对O 点的位矢r 与极轴的夹角θ称为角位置。

引入角速度、角加速度，由于刚体是个特殊质点组，即各质元之间没有相对移动，因此，在同一转动平面上，它们的角量(即角位移、角速度、角加速度)都相同，但由于各质元到轴的距离不同，因此各质元的线量(即线位移、线速度、线加速度)不同。

dt d θω= 22dt d dt d θωβ==ωR v = βτR a = 22ωR R v a n == 刚体作定轴转动时，每个质元的转动方向只有两种可能，如果以转轴为z 轴，则质元的角速度方向要么与所选z 轴正向相同，要么与所选z 轴正向相反．因此，刚体定轴转动时所有角量的方向，都可用标量前的正负号表示。

1、转动惯量

刚体转动时，刚 体内的各质点作圆周 运动，刚体的动能等 于各质点动能之和。
mn
m1
rn
r1
r2 m2
1 1 1 2 2 2 Ek m1v1 m2v2 mnvn 2 2 2 n n 1 1 2 2 mivi mi (ri ) i 1 2 i 1 2 1 n 2 2 ( miri ) 2 i 1
1 l 1 2 2 J ml m ml 结果与前相同。 3 12 2
t
0
1 2 0 0 t t 2
v v 2a( x x0 )
2 2 0
2 ( )
2 2 0 0
匀变速转动
六 角量与线量之间的关系
1、位移与角位移之间的关系 刚体转过 刚体上的一点 位移 s
o
r
s
x
s r
第六章 刚体力学
本章主要内容：
6－1 刚体的运动 6－2 刚体的角动量、转动动能、转动惯量
6－3 力矩
刚体定轴转动定律
6－4 定轴转动的动能定理 6－5 刚体对定轴的角动量守恒定律
6－6 进动*
本章学习要求
2.理解转动惯量、力矩的概念，掌握转动定律。 3.掌握刚体转动的动能定理、角动量定理。
1.掌握刚体定轴转动的特点，理解角坐标、角位移 角速度、角加速度的概念。
1 n 刚体的转动动能 Ek ( miri2 ) 2 2 i 1 1 2 与平动动能比较 Ek mv 2 n 2 miri ：相对于转轴的特征的物理量
i 1
转动惯量的定义：
单位：kg ·m2
J m r
i 1

vi θ
P
Δmi
o
转动平面
x
op r
2.定轴转动的角量描述 1.角位置θ
2.角位移
Ｐ 方向与转动方向成右手螺旋法则。 o θ X 转动平面 op r P点线速度 v r d ( rad / s 2 ) 4. 角加速度矢量 dt 由于在定轴转动中轴的 当加速转动时, 与 方向相同； 方位不变，故 , 只 有沿轴的正负两个方向， 当减速转动时, 与 方向相反;
Δmｊ
质元
Δmi
ｒ iｊ
2. 刚体的运动形式: ⑴平动： 在描述刚体的平动时,可以用一点的运 动来代表，通常就用刚体的质心的运动来 代表整个刚体的平动。
⑵转动: 转动是刚体的基本运动形式之一。 刚体转动时各质元均做圆周运动,而且 各圆的圆心都在一条固定不动的直线上, 这条直线叫转轴。如果转轴方向不随时间 变化, 则称定轴转动。
d 3.角速度: 单位：rad/s dt 角速度是矢量 。
Z
ω 转动方向 v
可以用标量代替。
５.当角加速度是常量时： 0 t
( 0 ) t 1 t 2 2
2 2 0 2 ( 0 )
P点线加速度 a r
an r
转轴
⑶ 刚体的一般运动都可以认为是平动和绕某一转轴转动 的结合。如图,车轮的转动。
二、刚体定轴转动的描述 1.特点: 其上各质元都在垂直于转轴的平面内作圆周运动, 且所有质元的矢径在相同的时间内转过的角度相同. 一般用角量描述。 转动平面: 取垂直于转轴 的平面为参考系, 称转动平面。,
转轴 Z
转动方向
刚体的角动量
L J

62钟摆绕o轴转动惯量jo等于杆绕o的转动惯量加上盘绕o的转动惯量63圆环转轴通过中心与盘面垂直常见刚体转动惯量64薄圆盘转轴通过中心与盘面垂直圆柱体转轴通过中心与几何轴垂直12mlmr细棒转轴通过中心与棒垂直12细棒转轴通过端点与棒垂直672r球体转轴沿直径2r球壳转轴沿直径68质点系的角动量定理
可能出现的情况是
（请点击你要选择的项目）
（4）以上结果都不对。
小议分析
质点系 若 T1 T2
系统的末 态角动量 忽略轮、绳质量及轴摩擦 系统受合外力矩为零，角动量守恒。 系统的初 态角动量 不论体力强弱，两人等速上升。
得
若 同高从静态开始 往上爬
系统受合外力矩不为零，角动量不守恒。 可应用质点系角动量定理进行具体分析讨论。
某过程角动量守恒要求整个过程的每个瞬间的系统角动量 保持不变。 角动量守恒条件是合外力矩始终为零，而非冲量矩为零
（只要初末状态角动量相等）
O

m
t2
b
O
t1
M dt L2 L1
以O’为参考点，球运动一周，始末状态角动量 相等，但是这个过程角动量不守恒。
L mvb
π （b与v夹角为 ） 2
( e)
( e)
外力矩：系统所受外力对质点i 的
力矩
量定理
对其中的一个质点i而言：
Li ri Fi ri (Fi (i ) Fi (e) ) Mi (i ) Mi (e)
对整个质点系而言：
(i ) (e) dLi dL (i ) (e) ri ( Fi Fi ) M i M i dt dt i i i i
质点所受合外力的冲量矩等于质点角动量的增量. 这是质点角动量定理的积分形式

3. 同一方程式中所有量都必须相对同一转轴。
(12)
例1、如图所示，A、B为两个相同的绕着轻绳的定滑
轮．A滑轮挂一质量为M的物体，B滑轮受拉力F，而且
F＝Mg．设A、B两滑轮的角加速度分别为βA和β B，
不计滑轮轴的摩擦，则有
(A) β A＝ β B． (B) β A＞ β B． (C) β A＜ β B． (D) 开始时β A＝ β B，以后β A＜ β B.
转动惯量的计算
1)定义 J miri2
J r 2dm
i
m
2) 对称的 简单的 查表
3) 平行轴定理
典型的几种刚体的转动惯量
m
m
l
细棒转轴通过中 心与棒垂直
J ml 2 12
l
细棒转轴通过端 点与棒垂直
J ml 2 3
M，R
M，R
o
圆环转轴通过环心与环面垂直
J MR2
薄圆盘转轴通过 中心与盘面垂直
以 m1 为研究对象 m1g T1 m1a 以 m 2 为研究对象 T2 m2a 以 M 为研究对象
(T1 T2 )R J J 1 MR 2 2
m 2 T2 M , R
（1） T1
T1
（2）
m1
m1
M ,R
m1g （3）
T2
m2
T2
T1
补充方程：
a R
（4）
联立方程（1）---（4）求解得
J 1 MR 2 2
m 2r
r l
球体转轴沿直径
J 2mr 2 5
圆柱体转轴沿几何轴
J 1 mr 2 2
转动定律应用举例 解题步骤: 1. 认刚体;
3. 分析力和力矩;

偏转角为30°。问子弹的初速度为多少。
o
解： 角动量守恒：
30°
mva 1 Ml 2 ma 2
la
3
v
机械能守恒：
1 1 Ml 2 ma 2 2 mga1 cos 30 Mg l 1 cos 30
23
2
v 1 g 2 3 Ml 2ma Ml 2 3ma 2 ma 6
刚体可以看成是很多质元组成的质点系，且在外力 作用下，各个质元的相对位置保持不变。 因此，刚体的运动规律，可通过把牛顿运动定律应 用到这种特殊的质点系上得到。
3
2.刚体的运动
平动：刚体在运动过程中，其上任意两点的连线 始终保持平行。
刚体的平动可看做刚体质心 的运动。
转动：刚体中所有的点都绕同一直线做圆周运动. 转动又分定轴转动和非定轴转动 .
r2dm
L
r2 dl
L
（线质量分布）
12
3 平行轴定理
如果刚体的一个轴与过质 心轴平行并相距d，则质量 为 m 的刚体绕该轴的转动 惯量，等于刚体绕过质心 轴的转动惯量与 md2 之和：
J z Jc md 2
请同学们自己证明平行轴定理的。
提示：利用余弦定理 ri2 ri '2 d 2 2dxi 13
hc hi
若A外+ A内非=0
Ep=0
则Ek +Ep =常量。
例13 一均质细杆可绕一水平轴旋转，开始时处于 水平位置，然后让它自由下落。求： ( )
解 方法一 动能定理
M mg L cos
2
W
Md
mg
L cosd
0
0
2
mg L sin
2
θ