11.3.1多边形导学案

八年级数学上册《11.3.1 多边形》导学案（新版）新人教版11、3、1 多边形学习目标１、能正确1、理解多边形、凸边形、正多边形、多边形的内角、外角、对角线的定义。

２、能正确2、推导多边形内角和公式和多边形外角和定理。

３、初步能3、运用多边形内角和和外角和解决实际生活中的问题。

重难点重点：推导多边形内角和公式和多边形外角和定理难点：运用多边形内角和和外角和解决实际生活中的问题前置学习（课前独学20分或30分钟）1、自主学习1、什么样的图形叫多边形？2、指出下面图1的内角和图2的外角。

3、画出下面多边形的所有对角线。

思考：从多边形的一个顶点处能引几条对角线。

多边形共有条对角线？二、跟踪练习：1、过m边形的一个顶点有7条对角线，n边形没有对角线，k 边形对角线条数等于边数，则m= ，n= ，k= 。

2、四边形的一条对角线将四边形分成几个三角形？从五边形的一个顶点出发，可以画出几条对角线？它们将五边形分成几个三角形？课堂学习流程总结反思一、前置学习展示交流5-10分钟：（对学群学）（一）学生提出的问题：（二）注意事项：（师生总结，学生整理）二、分层训练（20分钟）（一）双基过关（二）能力提升从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n 的值是（）A、6B、7C、8D、9三、课堂小结（5分钟）◆ 总结所学，建构知识：四、达标反馈（10-15分钟）必做题：1、从n边形的一个顶点出发可以画条对角线，这些对角线把这个n边形分成了个三角形。

2、把一张形状是多边形的纸片剪去其中某一个角，剩下的部分是一个四边形，则这张纸片原来的形状不可能是（）A、六边形B、五边形C、四边形D、三角形3、画出下列多边形的全部对角线：选做题：凸n边形的对角线的条数记作an（n≥4），例如：a4=2，那么：①a5= ；②a6-a5= ；③an+1-an= 、（n≥4，用n含的代数式表示）时间______________评价_____________。

一、新课导入1.导入课题：请同学们仔细观察下面的三个图形，它们给我们以由一些线段围成的图形的形象，这些图形叫做什么形呢？这节课我们就来学习多边形.2.学习目标：（1）能叙述多边形、多边形的内角、外角和对角线的意义.（2）知道什么是凸多边形和正多边形.3.学习重、难点：重点：多边形及其有关的概念.难点：多边形的边的特征.二、分层学习1.自学指导：（1）自学内容：教材第19页的内容.（2）自学时间：5分钟.（3）自学方法：认真阅读课文，可以结合下面的自学参考提纲学习，通过观察、比较，初步建立边的概念，初步认识四边形、五边形、六边形等平面图形，理解多边形、多边形的内角及其外角的定义.（4）自学参考提纲：①认识多边形a.回忆三角形的概念，说说多边形的概念.在平面内，由一些线段首尾顺次相接组成的封闭图形叫做多边形.b.下面这些图形分别是几边形？五边形六边形八边形如果一个多边形由n条线段组成，那么这个多边形就叫做n边形.②认识多边形的内角、外角多边形的内角是多边形相邻两边组成的角，多边形的外角是多边形的边与它的邻边的延长线组成的角，指出图2中多边形ABCDEF的外角∠1,∠2,∠3,∠4,∠5,∠6.③列举出我们生活中见到的多边形.2.自学：同学们可参照自学参考提纲进行自学.3.助学：(1)师助生：①明了学情：在日常生活中，学生接触的多边形比较多，本层次的内容学生能够很快掌握.②差异指导：引导学生列举出生活中的多边形.(2)生助生：学生之间相互交流学习的成果和困惑.4.强化：(1)多边形及其有关的角的概念.(2)练习：下列图形包含了哪些多边形？六边形四边形五边形和六边形1.自学指导：（1）自学内容：教材第20页内容.（2）自学时间：5分钟.（3）自学方法：认真阅读课本，抓住各个概念中的关键词.（4）自学参考提纲：①什么叫多边形的对角线？连接多边形不相邻的两个顶点的线段，叫做多边形的对角线.②什么叫凸多边形？指出下列多边形哪些是凸多边形.画出多边形任何一条边所在直线，整个多边形都在这条直线的同一侧，这样的多边形叫做凸多边形.a,c,e是凸多边形.③什么叫正多边形？正多边形有什么特征？各个角都相等，各条边都相等的多边形叫做正多边形.正多边形各个角相等，各条边相等.④试从四边形、五边形、六边形中探究n边形的对角线条数m与边数n之间的关系.m=n(3)2n(n≥4)2.自学：同学们可参照自学指导进行自学.3.助学：（1）师助生：①明了学情：多边形的对角线比较多，一般学生会有疏漏，应注意了解.②差异指导：引导学生领会对角线的重要应用是它可以把多边形分为几个三角形，从而把多边形的问题转化为三角形的问题来解决.（2）生助生：学生之间相互交流帮助.4.强化：（1）多边形的对角线的定义，正多边形的定义.（2）练习：画出右图多边形的全部对角线.（3）完成教材第21页练习第2题.答：四边形的一条对角线将四边形分成2个三角形，从五边形的一个顶点出发，可以画出2条对角线，它们将五边形分成了三个三角形.三、评价1.学生自我评价（围绕三维目标）：学生当众交谈自己的学习收获和困惑.2.教师对学生的评价：(1)表现性评价：对学生的学习态度、方法、成效和存在的不足进行点评.(2)纸笔评价：课堂评价检测3.教师自我评价（教学反思）:学习本课时，可让学生先自主探索再合作交流，小组内、小组之间充分交流后概括所得结论，既巩固了三角形的知识，又用类比的方法引出多边形的有关概念，加深对本课时的学习.一、基础巩固（每小题10分，共50分）1.六边形的对角线共有（D）2.下列属于正多边形的是（B）3.从一个顶点出发的对角线，可以把十边形分成互不重叠的三角形的个数（B）4.四边形有2条对角线，五边形有5条对角线，十边形有35条对角线.5.十二边形共有54条对角线，过一个顶点可作9条对角线，可把十二边形分成10个三角形.二、综合应用（20分）6.某学校七年级六个班举行篮球比赛，比赛采用单循环积分制（即每个班都进行一次比赛）.一共需要多少场比赛？解：一共需要15场比赛.如图：三、拓展延伸（30分）7.四边形中，过一个顶点可画一条对角线，共可画两条对角线；五边形中，过一个顶点可画两条对角线，共可画五条对角线；六边形中，过一个顶点可画三条对角线，共可画九条对角线，请从以上三种情况寻找一下规律，看一看多边形的边数和对角线之间有关系吗？如果有，请找出来.如果是n边形，可画多少条对角线呢？解：有关系，多边形对角线的条数等于边数与（边数-3）的乘积的12即n边形对角线的条数=n(3)2n.。

11.3.1 多边形导学案一、学习目标1.了解多边形的定义及分类；2.掌握多边形内角和、外角和的计算公式；3.能够运用多边形的性质解决实际问题。

二、思考问题1.什么是多边形？多边形的常见分类有哪些？2.如何求多边形的内角和、外角和？它们又有何特点？3.在日常生活中，你能想到与多边形相关的例子吗？三、学习内容1. 多边形的定义和分类多边形是由多条线段所组成的封闭图形。

其中，相邻两条线段所形成的角称作内角，而多边形中的所有内角和称为多边形的内角和。

多边形的常见分类有以下几种：•三角形：由三条线段所组成的多边形；•四边形：由四条线段所组成的多边形；•五边形：由五条线段所组成的多边形；•六边形：由六条线段所组成的多边形；•…2. 多边形的内角和和外角和根据多边形的定义以及角的性质，可以得到以下结论：•三角形的内角和为180度；•四边形的内角和为360度；•n边形的内角和为(n-2)×180度。

在多边形中，每个内角都与它的对角线之间存在对应关系，即它们的和为180度。

因此，多边形中的外角和等于360度。

3. 运用多边形的性质解决问题多边形的性质经常被应用于日常生活和各种工作中，例如：•工程设计：如房屋的建造、道路的铺设等；•艺术设计：如绘画、雕塑等；•游戏娱乐：如拼图、棋类游戏等；•…四、思考题解答1.多边形是由多条线段所组成的封闭图形。

常见的多边形分类有三角形、四边形、五边形、六边形等。

在学习多边形时，需要掌握各种多边形的定义及性质。

2.求多边形的内角和，可以根据内角定义的几何关系，得到其公式为(n-2)×180度。

求多边形的外角和，可以根据外角的定义和几何关系，得到其公式为360度。

需要注意的是，多边形内角和公式只适用于凸多边形。

3.多边形的性质在日常生活中有着广泛的应用，例如建筑设计中的房屋、道路的建造、艺术设计中的绘画、雕塑等等。

此外，多边形还有被广泛应用在游戏娱乐领域，比如拼图、棋类游戏等等。

新人教版八年级数学上册11.3.1多边形导学案【教学目标】1．知道多边形及有关概念；2．能区别凸多边形与凹多边形．【教学重点】多边形及有关概念【教学难点】多边形及有关概念【教学过程】活动一认识多边形1．阅读课本,从书上找出几个由一些线段围成的图形，并试着说出它们的名称.2．⑴仿照三角形的定义给多边形定义:_____________________________ _____叫做多边形．说说下图是几边形? 如何表示?⑵指出下图多边形的边、顶点、内角和外角．边角顶点外角⑶画出下图多边形的对角线．思考：n边形的共有几条对角线呢?(组内交流)活动二识别凸多边形与凹多边形及正多边形．(先独立完成后小组交流)1.阅读课本说说哪个是凸多边形? 哪个是凹多边形?如何识别?个案（师）或纠错（生）1 / 32 / 32．察下列正多边形，你能说出它们各自的特征吗【检测反馈】1．连接多边形 ___ __ 的线段，叫做多边形的对角线．过n边形的一个顶点能引条对角线，过n边形的n个顶点能引条对角线，过n边形的一个顶点所引的对角线把n边形分成个三角形。

2．多边形的任何 ____ 所在的直线，整个多边形都在这条直线的 ___，这样的多边形叫凸多边形．3．各个角，各条边的多边形，叫正多边形．4．画出下图中的六边形ABCDEF的所有对角线．5．如图（2），O为四边形ABCD内一点，连接OA、OB、OC、OD可以得几个三角形？它与边数有何关系？如图（3），O在五边形ABCDE的AB上，连接OC、OD、OE，可以得到几个三角形？它与边数有何关系？个案（师）或纠错（生）3 / 3。

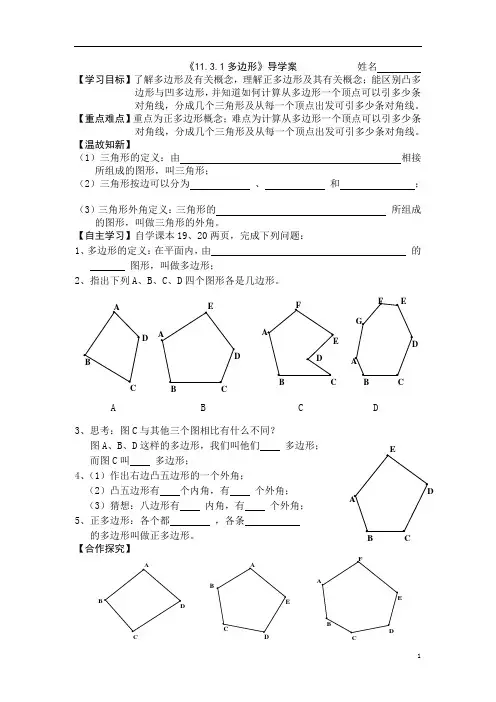
《11.3.1多边形》导学案 姓名【学习目标】了解多边形及有关概念，理解正多边形及其有关概念；能区别凸多边形与凹多边形，并知道如何计算从多边形一个顶点可以引多少条对角线，分成几个三角形及从每一个顶点出发可引多少条对角线。

【重点难点】重点为正多边形概念；难点为计算从多边形一个顶点可以引多少条对角线，分成几个三角形及从每一个顶点出发可引多少条对角线。

【温故知新】（1）三角形的定义：由 相接所组成的图形，叫三角形；（2）三角形按边可以分为 、 和 ；（3）三角形外角定义：三角形的 所组成的图形，叫做三角形的外角。

【自主学习】自学课本19、20两页，完成下列问题： 1、多边形的定义：在平面内，由 的 图形，叫做多边形；2、指出下列A 、B 、C 、D 四个图形各是几边形。

3、思考：图C 与其他三个图相比有什么不同？图A 、B 、D 这样的多边形，我们叫他们 多边形； 而图C 叫 多边形； 4、（1）作出右边凸五边形的一个外角；（2）凸五边形有 个内角，有 个外角； （3）猜想：八边形有 内角，有 个外角； 5、正多边形：各个都 ，各条 的多边形叫做正多边形。

【合作探究】A B CDA B CDEFABCDEC DB CBC B CA B DCBC1、从四边形的一个顶点可以引多少条对角线？n边形呢？2、从四边形的一个顶点引对角线可以把四边形分成几个三角形？n边形呢？3、从四边形的每个顶点引对角线可以引多少条？n边形呢？【达标检测】1、选择题（）（1）在同一平面内，四条线段首尾顺次连接组成的图形叫四边形。

（2）由四条线段首尾顺次相接组成的图形是四边形。

（3）各边都相等的多边形是正多边形。

（4）各角都相等的多边形不一定是正多边形。

（5）正多边形的各个外角都相等。

A、1个B、2个C、3个D、4个2、六边形的对角线的条数为（）A、15B、9C、8 D 、63、填空题：（1）从九边形的一个顶点出发，能引出条对角线，它们将九边形分成个三角形，九边形一共有条对角线。

11.3.1 多边形一、 自主探究1. 多边形相关概念(1)定义：平面内， 由 些线段首尾 所组成的 图形叫多边形，多边形有几条边就叫几边形.(2)多边形的内角：在多边形中， 所组成的角叫多边形的内角(3)外角：多边形的边与 所组成的角叫多边形的外角(4)对角线：连接多边形 的线段叫多边形的对角线画出右图多边形的全部对角线：(5) 个n边形，从 介顶点出发可引 条对角线，把n边形分成 个三角形，(6) n边形一共有 条对角线.(7)正多边形： 、 的多边形叫正多边形2 多边形的分类: 和3.凸多边形定义：画出多边形的任何一边所在直线，如果整个多边形都在这条直线 ，那么这个多边形就是凸多边形.二、典例分析例1、判断下列说法是否正确，若不正确，举出反例.(1) 所有的角都相等的多边形是正多边形 ( )(2) 所有边都相等的多边形是正多边形 ( )(3) 所有的多边形都有对角线( )(4) 正多边形的各条对角线都相等( )例2、(1) 从多边形一个顶点可引出．6条对角线，求边数；(2) 如果一个多边形共有 14条对角线，求边数；(3) 一个多边形的边数等于对角线的条数，求边数.例3、过n边形一个顶点有 2m条对角线，m边形没有对角线，k边形共有k条对角线，求((n−k) m的值.例4、有两个多边形，边数之比为2：3，对角线条数比为1：3，求这两个多边形的边数.三、拓展提高如图，在四边形 ABCD的纸片中，只剪一刀，剪去∠D，剩余部分是几边形? 请画出图形.四、限时作业1. 下列多边形中，不是凸多边形的是( )2. 下列说法正确的是 ( )A. 各边相等的多边形叫正多边形B. 各角相等的多边形叫正多边形C. 各边或各角相等的多边形叫正多边形D. 各边相等、各角相等的多边形叫正多边形3. 十六边形的对角线有 条.4. 若经过多边形的一个顶点有 27 条对角线，则这个多边形有 条边.5 若 个多边形共有 14条对角线，则它是 边形6.过m边形的一个顶点有7条对角线，n边形没有对角线，k边形共有k条对角线，则(m −k,ⁿ=7. 如果从一个多边形的一个顶点出发作它的对角线，最多能将多边形分成6个三角形，那么这个多边形有 条对角线8.若一个多边形截去1一个角后，变成十四边形，则原来的多边形的边数可能为( )A. 14 或 15B. 13 或14C. 13 或14 或15D. 14 或15 或16。

11.3.1 多边形导学案-2022-2023学年人教版八年级上册数学一、导学目标1.理解多边形的定义；2.掌握常见多边形的名称和性质；3.能够计算多边形的内角和外角。

二、导学内容2.1 多边形的定义多边形是由三条或三条以上的线段相连所形成的封闭图形。

多边形的每条边都是两个相邻的顶点间的线段，每个顶点都是两条相邻边的交点。

2.2 常见多边形的名称和性质1.三边形：有三条边和三个顶点，三个内角的和为180度；2.四边形：有四条边和四个顶点，四个内角的和为360度；3.五边形：有五条边和五个顶点，五个内角的和为540度；4.六边形：有六条边和六个顶点，六个内角的和为720度；5.八边形：有八条边和八个顶点，八个内角的和为1080度。

2.3 多边形的内角和外角的计算公式1.多边形的内角和公式：对于一个n边形，其内角和可以通过公式计算：内角和 = (n - 2) × 180度；2.多边形的平均内角公式：对于一个n边形，其平均内角可以通过公式计算：平均内角 = 内角和 / n；3.多边形的外角和公式：对于一个n边形，其外角和总是等于360度；4.多边形的平均外角公式：对于一个n边形，其平均外角总是等于360度 / n。

三、导学要点总结•多边形是由三条或三条以上的线段相连所形成的封闭图形；•常见多边形包括三边形、四边形、五边形、六边形和八边形；•多边形的内角和公式为 (n - 2) × 180度，平均内角为内角和 / n；•多边形的外角和总是等于360度，平均外角总是等于360度 / n。

四、练习题1.一个五边形的内角和是多少度？2.一个六边形的平均内角是多少度？3.一个八边形的外角和是多少度？4.一个四边形的平均外角是多少度？五、解答1.五边形的内角和 = (5 - 2) × 180度= 3 × 180度 = 540度。

2.六边形的平均内角 = 内角和 / 6 = 720度 / 6 = 120度。

名师讲坛例题1：已知过m 边形的一个顶点有7条对角线，n 边形没有对角线，k 边形共有k 条对角线，求n k m )(-的值 分析：n 边形一个顶点的对角线条数为)3(-n ,n 边形共有对角线的条数为2)3(-n n由此可推出k n m ,,的值。

解答：由题意：73=-m 02)3(=-n n ，k k k =-2)3(得：5,3,10===k n m 所以：153)510()(=⨯-=-n k m注意：理解多边形对角线的条数与边数的关系是解决本题的关键。

例题2：一个多边形截去一个角后，变成十六边形，则原来的多边形的边数是_________容易错解：15错因分析：一个多边形截去一个 预习导学 知识梳理1.多边形的概念：（1）定义：在平面内，由一些线段________________的封闭图形叫做多边形。

（2）如果多边形的各边都在___________________，这样的多边形叫做凸多边形。

（3）_______________________的多边形叫做正多边形。

2.多边形的对角线 （1）连接多边形________________________的线段叫做多边形的对角线 （2）从n 边形一个顶点可以引_____________条对角线，它们将多边形分成_________个三角形。

合作探究： 3.一个八边形有_________条边，有______个内角，有_______个外角（每个顶点处只计一个），从一个顶点出发可以引_______对角线，一共可以画__________条对角线。

随堂检测 知识点1. 认识多边形 1.从一个n 边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n 的值是（ ） A ．6 B. 7 C. 8 D. 9 11.3.1 多边形。

少林学校八年级数学导学案_____班_____组姓名：_________集体研备：初二数学组复备：房素云备课时间：2016/9/3 授课时间：11.3.1多边形学法指导学习目标： 1、掌握多边形、正多边形、多边形的内角、外角及多边形的对角线等数学概念。

2、掌握多边形的对角线条数与多边形边之间的关系，并运用其进行简单的计算。

学习重点：对上述概念的理解及对凸、凹多边形的理解学习难点：1、探究多边形的对角线的条数与多边形的边数之间的关系。

2、对正多边形的正确理解。

导学过程一．知识回顾：三角形的内角和等于------，外角和等于-----。

二、自主学习：认识多边形1、类比三角形得出多边形定义：在平面内，由一些线段-----------组成的图形。

注意：（1）是最简单的多边形（2）一个多边形由几条线段组成，就叫几边形。

如由四条边组成就叫四边形，由五条边组成就叫五边形。

如果一个多边形由n条线段组成，那么这个多边形就叫做，2，多边形-------两边组成的角叫做多边形的内角。

多边形的边与它的----------------组成的角叫做多边形的外角。

连接多边形----------------------的线段叫做多边形的对角线。

3，画出多边形的任何一条边所在的直线，整个多边形在这条直线的------------的多边形叫做凸多边形。

不都在同一侧的叫做凹多边形。

4,正多边形定义：各个角--------，各条边-------的多边形。

举例：-------------------------等。

针对练： E D 1）、如图，是边形， F记作：； A有条边，------个角，-------顶点。

CB2）、n边形有条边，个顶点，个内角。

3）、多边形有和之分。

4）：下列图形中是凸多边形的有①②③④三．展示评价：总结多边形的有关概念。

四、合作探究：多边形对角线的条数画一画，数一数，填写下表。

从四边形的一个顶点出发，可画条对角线，将四边形分成个三角形，共有条对角线；从五边形的一个顶点出发，可画条对角线，将五边形分成个三角形，共有条对角线；……n边形呢？填写下表：多边形的边数(n) 4 5 6 7 8 9 10 … n从一个顶点出发引的对角线条数上述对角线所分三角形个数多边形对角线总条数结论：1、从n边形的一个顶点可以引条对角线，将多边形分成个三角形。

八年级数学第十一章《11.3.1多边形》导学案（7）备课人：余国霞审核人：陈军营备课时间：8.31 上课时间：学习目标：1、理解正多边形及其有关概念．2、区别凸多边形与凹多边形．学习重点、难点：重点：理解正多边形及其有关概念．难点：准确理解多边形定义．学习过程：一、自主学习1、仔细观察课本19页的图，你能找出几个由一些线段围成的图形吗？这些线段围成的图形有何特点？答：（1）它们在同一内．（2）它们是由不在同一条直线上的几条线段组成的．2、你能仿照三角形的定义给多边形定义吗？（1）多边形的定义：在平面内，由一些线段____________________组成的图形叫做多边形．如果一个多边形由n条线段组成，那么这个多边形叫做__________边形．（一个多边形由几条线段组成，就叫做几边形．）（2）多边形的边、顶点、内角和外角．多边形组成的角叫做多边形的__ _，多边形的边与组成的角叫做多边形的_________．（3）多边形的对角线连接多边形的_______________的两个顶点的线段，叫做多边形的对角线．（4）凸多边形与凹多边形在图（1）中，画出四边形ABCD的任何一条边所在的直线，整个图形都在这条直线的同一侧，这样的四边形叫做_____四边形，这样的多边形称为_____多边形；而图（2）就不满足上述凸多边形的特征，因为我们画BD所在直线，整个多边形不都在这条直线的同一侧，我们称它为_________多边形。

注意：今后我们在习题、练习中提到的多边形都是凸多边形．（6）．正多边形：____________________的多边形叫做正多边形．二、学以致用（一）、判断题．1．由四条线段首尾顺次相接组成的图形叫四边形．（）2．由不在一直线上四条线段首尾次顺次相接组成的图形叫四边形．（）3．由不在一直线上四条线段首尾顺次接组成的图形，且其中任何一条线段所在的直线、使整个图形都在这直线的同一侧，叫做四边形．（）4．在同一平面内，四条线段首尾顺次连接组成的图形叫四边形．（）（二）、解答题．画出图中的六边形ABCDEF的所有对角线．三、当堂检测1、从四边形的一个顶点出发，可以画出条对角线，将四边形分成个三角形；从五边形的一个顶点出发，可以画出条对角线，将五边形分成个三角形；从六边形的一个顶点出发，可以画出条对角线，将六边形分成个三角形；从七边形的一个顶点出发，可以画出条对角线，将七边形分成个三角形；从n边形的一个顶点出发，可以画出条对角线，将n边形分成个三角形；n边形共有条对角线。

11.3.1 多边形导学案 2022—2023学年人教版数学八年级上册一、学习目标•理解多边形的定义和性质；•掌握计算多边形的边数、角数和对角线数的方法；•能够在平面坐标系中绘制多边形。

二、学习重点•多边形的定义和特点；•多边形边数、角数和对角线数的计算方法；•平面坐标系下多边形的绘制。

三、学习工具•教材；•笔记本电脑或电子设备；•白板或黑板；•笔和尺子。

四、学习内容1. 多边形的定义和特点多边形是由若干条线段首尾相接而构成的封闭图形。

多边形的特点包括以下几点：•多边形是平面图形；•多边形中的线段称为边；•多边形中的顶点是边的端点；•多边形的边和顶点数是相等的；•多边形的相邻两个边之间通过一个顶点构成一个角。

2. 多边形边数、角数和对角线数的计算方法多边形的边数要计算一个多边形的边数，只需要数一下多边形中的边的个数即可。

多边形的角数计算一个多边形的角数，需要使用以下公式：角数 = 边数 - 2多边形的对角线数计算一个多边形的对角线数，可以使用以下公式：对角线数 = 边数 * (边数 - 3) / 23. 平面坐标系下多边形的绘制要在平面坐标系下绘制一个多边形，可以按照以下步骤进行：1.在平面坐标系中选择一个起点，将其标记为多边形的一个顶点；2.从起点开始，根据给定的边长和角度，使用尺子和直尺绘制出多边形的其他边和顶点；3.最后一条边与起点连接，形成一个封闭图形，即多边形。

五、学习步骤1.学生阅读教材第11章第3节的相关内容，对多边形的定义和特点有基本了解。

2.学生通过计算实例，掌握计算多边形边数、角数和对角线数的方法。

3.学生进行练习，独立计算给定的多边形的边数、角数和对角线数。

4.教师示范在平面坐标系中绘制多边形的方法，让学生亲自练习。

5.学生和教师共同总结学习内容，回答相关问题。

六、学习小结通过本节课的学习，我们了解了多边形的定义和特点，掌握了计算多边形边数、角数和对角线数的方法，还学会了在平面坐标系中绘制多边形的技巧。

11.3.1多边形学习目标：1、了解多边形及有关概念，理解正多边形的概念．2、区别凸多边形与凹多边形．学习重点：多边形及有关概念、正多边形的概念学习难点：区别凸多边形与凹多边形：学习过程：自主学习1.复习回顾，如图，填空：（1）∠1＋∠2＋∠3＝；（2）∠4＋∠5＋∠6＝；（3）∠4＝∠＋∠；∠5＝＋；（4）∠6 > ∠；∠6 > ∠二、合作交流探究与展示：问题：学习多边形的有关概念,阅读课本第19至20页，回答：1、由一些线段首尾顺次相接组成的图形叫做。

多边形按组成它的线段的条数分成三角形、四边形、五边形……、n边形。

这就是说，一个多边形由几条线段组成，就叫做几边形，三角形是最简单的多边形。

2、如果一个多边形由n条线段组成，你们这个多边形就叫做n边形，填空：边形边形边形与三角形类似地，多边形相邻两边组成的角叫做多边形的内角，如图中的∠A、∠B、∠C、∠D、∠E。

多边形的边与它的邻边的延长线组成的角叫做多边形的外角．如图中的∠1是五边形ABCDE的一个外角。

3、连接多边形不相邻的两个顶点的线段，叫做多边形的。

4、(1)如图，请画出下列多边形中的A点与其他顶点的对角线，并回答问题：四边形被对角线分成个三角形五边形被对角线分成个三角形四边形有几条对角线？五边形有几条对角线？你能猜想n边形有多少条对角线吗？说说你的想法。

n边形有条对角线。

因为从n边形的一个顶点可以引条对角线，n个顶点共引条对角线，又由于连接任意两个顶点的两条对角线是相同的，所以，n边形有条对角线（2）如图，下面的两个多边形有什么不同？在图（1）中，画出四边形ABCD的任何一条边所在的直线，整个图形都在这条直线的同一侧，这样的四边形叫做凸四边形，这样的多边形称为凸多边形；而图（2）就不满足上述凸多边形的特征，因为我们画BD 所在直线，整个多边形不都在这条直线的同一侧，我们称它为凹多边形。

注意：今后我们讨论的多边形指的都是凸多边形．判断下列图形是凸多边形有；5.正多边形:我们知道，等边三角形、正方形的各个角都相等，各条边都相等，像这样各个角都相等，各条边都相等的多边形叫做正多边形。

第十一章 三角形
多边形及其内角和
11.3.1 多边形
.
.
. . .
?
二、新知预习 自主归纳：
_______相接组成的如果一个多边形由n 条线段组成，那么这个多边形就A,∠B,∠C,∠D,∠E 是五边形_______________组成的角叫做多边形的的两个顶点的线段，叫做多边形的对角线,线段_________
是五边形ABCDE 的对角线.画出多边形的任意一条边所在的直线，如果整个多边形都在这条直线的
___________的多边形叫做正多边形
方法总结:多边形可分为凸多边形和凹多边形，辨别凸多边形可有两种方法：
形任何一边所在的直线，整个多边形都在此直线的同一侧；
180°.通常所说的多边形指凸多边形．
例1 凸六边形纸片剪去一个角后，得到的多边形的边数可能是多少？画出图形说明．
画一画：画出下列多边形的全部对角线.
2.把一张形状是多边形的纸片剪去其中一个角，剩下的部分是一个四边形，则这张纸片原来的形状不可能是（ ）
A. 六边形 B . 五边形 C.四边形 D.三角形 3.九边形的对角线有（ ） A.25条
B.31条
C.27条
D.30条
4.若从一个多边形的一个顶点出发，最多可以引10条对角线，则这是 _______边形.
5.过八边形的一个顶点画对角线，把这个八边形分割成_______个三角形.。