19哈密顿正则方程

理论力学题库——第五章一、填空题1. 限制力学体系中各质点自由运动的条件称为 。

质点始终不能脱离的约束称为 约束，若质点被约束在某一曲面上，但在某一方向上可以脱离，这种约束称为 约束。

2. 受有理想约束的力学体系平衡的充要条件是 ，此即 原理。

3. 基本形式的拉格朗日方程为 ，保守力系的拉格朗日方程为 。

4. 若作用在力学体系上的所有约束力在任意虚位移中所作的虚功之和为零，则这种约束称为 约束。

5. 哈密顿正则方程的具体形式是 和 。

5-1. n 个质点组成的系统如有k 个约束，则只有 3n - k 个坐标是独立的. 5-2.可积分的运动约束与几何约束在物理实质上没有区别，合称为 完整约束 .5-3自由度可定义为：系统广义坐标的独立 变分数目 ，即可以独立变化的 坐标变更数 . 5-4.广义坐标就是确定力学体系空间位置的一组 独立坐标 。

5-5.虚位移就是 假想的 、符合约束条件的、无限小的、 即时的 位置变更。

5-6.稳定约束情况下某点的虚位移必在该点曲面的 切平面上 。

5-7.理想、完整、稳定约束体系平衡的充要条件是 主动力虚功之和为零 . 5-8.有效力（主动力 + 惯性力）的总虚功等于 零 。

5-9.广义动量的时间变化率等于 广义力 （或：主动力+拉氏力）。

5-10.简正坐标能够使系统的动能和势能分别用 广义速度 和 广义坐标 的平方项表示。

5-11.勒让德变换就是将一组 独立 变数变为另一组 独立 变数的变换。

5-12.勒让德变换可表述为：新函数等于 不要的变量 乘以原函数对该变量的偏微商的 和 ，再减去原函数。

5-13.广义能量积分就是 t 为循环坐标时的循环积分。

5-14. 泊松定理可表述为：若21),,(,),,(c t p q c t p q ==ψϕ是正则方程的初积分，则 []3c ,=ψϕ 也是正则方程的初积分.5-15.哈密顿正则方程的泊松括号表示为： ],[H p pαα= ； ],[H q q αα= 。

1
哈密顿正则方程
例1-13 半径为a 的光滑圆形金属圈，以匀角速ω绕铅直方向的轴z
转动，圈上套有一质量为m 的小环。

初始时，小环自圆圈的最高点无初
速地沿圆环下滑，试求当与圆圈中心的联线和铅直向上的z 轴成θ角时，
小环的运动方程。

解：这是一个非定常的完整系统，主动力有势。

应用哈密顿正则方程
求解，取广义坐标为θ。

系统的功能T 为
)sin (2
122222θωθa a m T += 系统的势能为
θcos mga V =
拉格朗日函数L 为 θθωθcos )sin (2122222mga a a m L -+= 为求哈密顿函数H ，先求广义动量p θ
θθ
θ 2ma L p =∂∂= 哈密顿函数H 为 θθωθθθθθcos sin 2122242222mga a a m p a m ma p p L p H +⎪⎪⎭⎫ ⎝⎛--=-=
正则方程为
θθθθp H p H -=∂∂=∂∂, 得到
θθ =p ma 21 (1) θθθθωp
mga ma -=--sin cos sin 22
(2)
2 由式（1）（2）得到
θ
θθθω 222sin cos sin a ga a -=-- 或者写成
θθθωθsin cos sin 2g a a += 哈密顿函数H 中不显含时间t ，有广义能量积分，即
h g a a '=+-θθωθcos sin 2
121222。

哈密顿力学哈密尔顿力学是哈密尔顿于1833年建立的经典力学的重新表述。

它由拉格朗日力学演变而来，那是经典力学的另一表述，由拉格朗日于1788年建立。

但它可以使用辛空间不依赖于拉格朗日力学表述。

关于这点请参看其数学表述。

哈密顿力学-简介哈密顿力学是标准的“伽利略加速点运动几何学”的一种力学。

不幸的是，后人将其称作是“新几何力学”，这多多少少显示了后人的数学知识和物理学思想的一种令人遗憾的欠缺。

哈密顿系统可以理解为时间R上的一个纤维丛E,其纤维Et,t∈R是位置空间。

拉格朗日量则是E上的jet丛(射流丛)J上的函数；取拉格朗日量的纤维内的勒让德变换就产生了一个时间上的对偶丛的函数，其在t 的纤维是余切空间T*Et，它有一个自然的辛形式，而这个函数就是哈密顿量。

任何辛流形上的光滑实值函数H可以用来定义一个哈密顿系统。

函数H称为哈密顿量或者能量函数。

该辛流形则称为相空间。

哈密顿量在辛流形上导出一个特殊的向量场，称为辛向量场。

该辛向量场，称为哈密顿向量场，导出一个流形上的哈密顿流。

该向量场的一个积分曲线是一个流形的变换的单参数族；该曲线的参数通常称为时间。

该时间的演变由辛同胚给出。

根据刘维尔定理每个辛同胚保持相空间的体积形式不变。

由哈密顿流到处的辛同胚的族通常称为哈密顿系统的哈密顿力学。

哈密顿向量场也导出一个特殊的操作，泊松括号。

泊松括号作用于辛流形上的函数，给了流形上的函数空间一个李代数的结构。

当余度量是退化的时，它不是可逆的。

在这个情况下，这不是一个黎曼流形，因为它没有一个度量。

但是，哈密顿量依然存在。

这个情况下，在流形Q的每一点q余度量是退化的，因此余度量的阶小于流行Q的维度，因而是一个亚黎曼流形。

这种情况下的哈密顿量称为亚黎曼哈密顿量。

每个这样的哈密顿量唯一的决定余度量，反过来也是一样。

这意味着每个亚黎曼流形由其亚黎曼哈密顿量唯一的决定，而其逆命题也为真：每个亚黎曼流形有唯一的亚黎曼哈密顿量。

亚黎曼测地线的存在性由Chow-Rashevskii定理给出。

§1.3哈密顿正则方程上一节，我们给出了拉格朗日函数的定义式 L T U =-，并且发现拉格朗日函数L 是广义坐标和广义速度的函数。

给出拉格朗日方程的表达式。

但拉格朗日方程是二阶常微分方程组。

为了使方程降阶，即由二阶变为一阶，我们引入了一个新的量，称为广义动量。

一、广义动量设体系的广义坐标为11,,,s q q q ，对于每一个广义坐标k q ，可以定义一个广义动量： k kLp q ∂=∂ （1） 式中L 为拉格朗日函数，k q 为广义速度。

大家注意，这里我们定义的广义动量和我们一般所说的动量的含义不一定相同。

例如，对于做平面圆周运动的质点，质点的自由度为1，为了研究方便，选方向角θ为广义坐标。

则质点的速度为：v r θ=，2221122T mv mr θ==， 2212L T mr θ==，广义动量2Lp mr θθθ∂==∂相当于通常意义上的动量矩。

二、哈密顿正则方程拉格朗日函数是广义坐标和广义速度的函数，即(,)L L q q =，它的全微分11ssk k k k k kL L dL dq dq q q ==∂∂=+∂∂∑∑ （2） 由拉格朗日方程()0k k d L L dt q q ∂∂-=∂∂和广义动量的定义式k kLp q ∂=∂得 k kLp q ∂=∂ （3） 将(1)(3)代入(2)中，dL 可写为11ssk k k k k k dL p dq p dq ===+∑∑ （4）而上式的第二项可写为111()ss skkk k k k k k k p dqd p q q d p ====-∑∑∑ （5）把（5）式代入（4）式得111()sssk k k k k k k k k dL p dq d p q q d p ====+-∑∑∑即111()sssk k k k k k k k k d p q L p dq q d p ===-=-+∑∑∑ （6）定义： 1sk k k H p q L ==-∑ 称作哈密顿函数所以（6）式可写为11ssk k k k k k dH p dq q d p ===-+∑∑ （7）由上式可以看出H 只是各个k q 和k p 的函数。

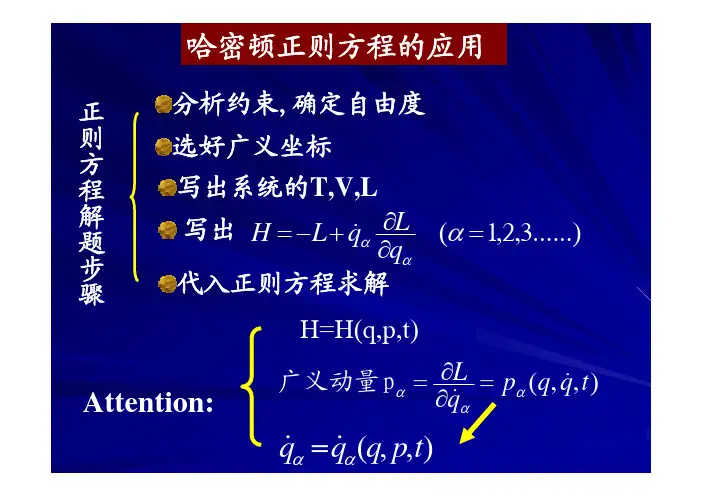
§6.哈密顿正则方程引言：哈密顿正则方程是与拉氏方程：0=∂∂-∂∂a a q L qL dt d 等价的动力学方程。

s q L q L dt d a a ,....2,10==∂∂-∂α ，这组拉氏方程是s 个关于广义坐标a q 的二阶常微分方程。

在这组拉氏方程中的拉氏函数L 它是广义坐标q ，广义速度q以及时间t 的函数：),,(t qq L L =。

如果我们把拉氏函数中的广义速度a q 变换成→广义动量αp ，即),,(t p q L L =那么就可以将上面的s 个拉氏方程①化成2s 个一阶常微分方程，而且这2s 个一阶常微分方程还具有一定的很漂亮的对称性②具有一定的对称性。

要想把拉氏函数：),,(t qq L L =变成是广义坐标、广义动量P 及时间t 的函数→),,(t p g L L =，以及将s 个拉氏方程化成2s 个一阶常微分方程。

将会用到勒襄特变换这一数学工具。

∴得先介绍一下：一．勒襄特变换（只作了解，不作要求，大纲不要求讲这部分内容）现在先讨论两个变量的勒襄德变换，假设所给的函数是两个变量x 1 和x 2的函数，即：),(21x x f f =。

则由高等数学的知识可得此函数的全微分：2211dx x f dx x f df ∂∂+∂∂=在此我们令11x f u ∂∂=,22x f u ∂∂=,[ii x f u ∂∂=(i=1,2)]……①并以1u 和2u 为新的变量定义一个新函数g: ∑=-+=-≡212211i i if u x u x f u xg ……②如果我们从变换方程①解出i x ，使i x 是i u 的函数，即)(i i i u x x =，再代入上式②中去，那么，g 就是只含新变量i u 的函数了，即：),(21u u g g =。

我们先对②式两边进行微分，则得：∑∑∑∑=====⎥⎦⎤⎢⎣⎡⋅∂∂-+=∂∂-+=21212121)()(i i i i i i i i i i i i i i i i i du x dx x f u du x dx x f dx u du x dg 又∵将旧变量i x 换成新变量i u 之后，新函数g 就是新变量i u 的函数：),(21u u g g =那么对它微分就有：2211du u g du u g dg ∂∂+∂∂=……*′，将这个等式与上一等式进行比较就可得到变换关系：11u g x ∂∂=，222du u g x ∂∂=……③前面我们利用变换方程①把旧的变量x 1,x 2及旧的函数),(21x x f 变为新的变量21,u u 及新的函数),(21u u g g =的方法，就称为勒让德变换。

正则变换的研究学生xx红河学院理学院物理学，云南省，中国，661100摘 要：正则变换是由一组正则变量到另一组能保持正则形式不变的变量的变换。

是解决正则方程的 解而引入的一种重要的变换方法。

关键词：正则变换；母函数；广义坐标。

1788年，拉格朗日写了一本大型著作《分析力学》。

在这一本著作中，完全用数学分析的方法来解决所有的力学问题。

而无需借助以往常用的几何方法，全书一张图都没有。

在基础上，逐步发展为一系列处理力学问题的新方法，称之为分析力学。

拉格朗日是用s 个独立变量来描写力学体系的运动，所以和牛顿运动方程一样，是二阶常微分方程组，我们通常把这组方程叫做拉格朗日方程。

后来，哈密顿在1834年又提出：如果用坐标和动量作为独立变量，则虽方程式的数目增加了一倍，由s 个变为2s 个，但微分方程式却都由二阶将为一阶。

这组方程叫哈密顿正则方程。

他在1843年又运用变分法提出了另一个和牛顿定律等价的哈密顿原理，用来描述力学体系的运动。

哈密顿正则变换将是求解哈密顿正则方程必不可少的一种计算方法。

本节将给出正则变换的目的、条件和变换形式。

（一）正则变换的目的和条件哈密顿函数是),...,2,1(,p s q =ααα及t 的函数，而哈密顿正则方程则是2s 个一阶微分方程。

如果H 中不出现某个q ，例如q i，则这个不出现q i就是循环坐标，而我们也将由正则方程式),...,2,1(q s H H q p p =⎪⎪⎭⎪⎪⎬⎫∂∂-=∂∂=ααααα ……（1） 力学体系的哈密顿函数H 中，有没有循环坐标，与我们所选的坐标系有关，在某种坐标系中没有循环坐标，在另一种坐标系中却可以有一个或几个循环坐标，有心力就是一个最明显的例子，在极坐标中，如质点的质量是m ，则动能)(m 21222θ r r T +=。

对平方反比引力问题来讲，势能rmV k2-=，故H=T+V.很显然，这里极角θ是一个循环坐标，故对应的广义动量的微分0p =∂∂=θθ L,即常数===∂∂=θθθ r m L2p即对应的广义动量是守恒的，在这里我们将介绍坐标和动量的变换，是新的哈密顿函数中出现一些循环坐标，如果通过某种变数的交换，能够找到新的函数，设为H*，使正则方程的形式不变，这种变换就叫正则变换。