哈密顿正则方程例题
- 格式:ppt
- 大小:1.46 MB
- 文档页数:13


1哈哈密密顿顿正正则则方方程程作作业业1.如果哈密顿函数L qp H s1-=∑=ααα 能表示成坐标αq 和动量αp 的函数,则无论H 是(a)明显不包含时间变量t,还是(b)明显包含时间变量t,哈密顿正则方程均为: αα∂∂=p H q ;αα∂∂-=q H p )s 2,1( =α 1.证明: (a)H 明显不包含时间变量t 时:对L qp H s1-=∑=ααα 微分,得: ∑∑∑∑=ααα=ααα=ααα=ααα∂∂-∂∂-+=s 1s1s 1s 1q d q L dq q L dp q q d p dH 而αα=∂∂p q L ; ααα=⎪⎪⎭⎫ ⎝⎛∂∂=∂∂p qL dt d q L (利用拉氏方程) 于是:∑∑=ααα=ααα-=s 1s 1dq p dp qdH 又哈密顿函数L qp H s1-=∑=ααα 能表示成广义坐标αq 和广义动量αp 的函数,即:∑∑=ααα=ααα∂∂+∂∂=s 1s1dp p H dq q H dH 比较上面两式可得:αα∂∂=p H q ;αα∂∂-=q H p )s 2,1( =α (b)H 明显包含时间变量t 时:对L qp H s1-=∑=ααα 微分,得: dt t L q d q L dq q L dp q q d p dH s 1s1s 1s 1∂∂-∂∂-∂∂-+=∑∑∑∑=ααα=ααα=ααα=ααα2 而αα=∂∂p q L ; ααα=⎪⎪⎭⎫ ⎝⎛∂∂=∂∂p qL dt d q L (利用拉氏方程) 于是:dt t L dq p dp qdH s 1s 1∂∂--=∑∑=ααα=ααα 又哈密顿函数L q p H s1-=∑=ααα 能表示成广义坐标αq 、广义动量αp 和时间t 的函数,即:dt t H dp p H dq q H dH s 1s1∂∂+∂∂+∂∂=∑∑=ααα=ααα 比较上面两式可得:αα∂∂=p H q ;αα∂∂-=q H p )s 2,1( =α,且t L t H ∂∂-=∂∂。

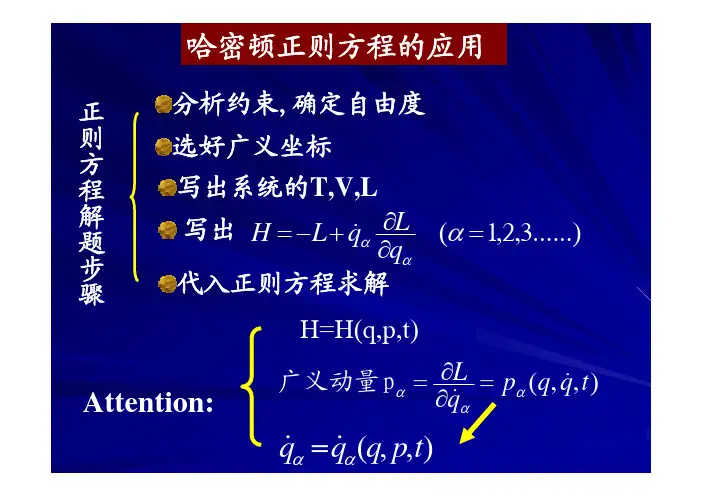

哈密顿正则方程
哈密顿正则方程为(1)式中H称为哈密顿函数,是广义动量pi和广义坐标qi及时间t的函数。
H由式(2)确定。
括号外边的角标表示式中的妜i应该用N个方程pi= 解出N 个妜i为(E1,E2,…,EN;q1,q2,…,qN;t)的N 个函数,然后代入式(2)就得到哈密顿函数H。
对于直角坐标变换到广义坐标的变换式虽然显含时间t,但是动能的表示式不明显地包含t,此时H=T2-T0+V,
式中T2和T0可说明如下:用(E1,E2,…,EN;q1,q2,…,qN;t)表示的动能式T=T2+T1+T0,式中T2、T1和T0分别表示广义动量的二次齐次式、一次齐次式和不含广义动量的项。
如果直角坐标变换到广义坐标的变换式不显含t,势函数V也不显含t,则T=T2,H=T+V。
即对于保守系统,哈密顿函数是系统总机械能用广义动量表示的公式。
正则方程式(1)是2N个一阶微分方程组,而拉格朗日方程是N个二阶微分方程组,都只适用于完整系统(见约束)的动力学方程组。
由于式(1)的左边不再有变数q和p的导数,所以方程(1)成为如下形式的方程组保守系统的正则方程在天体力学和经典统计力学中有重要的应用。
在天体力学中从可解的二体问题出发,逐渐添加其他星球的引力,可以把所用的哈密顿函数H,从简单改变成较复杂的H┡。
这是天体力学中的摄动法,用来解决考虑太阳和各种行星、卫星的引力作用下的行星运动,由此可制定行星和月球的星历表,在统计力学中的刘维定理
就是应用正则方程推导出来的。




1
哈密顿正则方程
例1-13 半径为a 的光滑圆形金属圈,以匀角速ω绕铅直方向的轴z
转动,圈上套有一质量为m 的小环。
初始时,小环自圆圈的最高点无初
速地沿圆环下滑,试求当与圆圈中心的联线和铅直向上的z 轴成θ角时,
小环的运动方程。
解:这是一个非定常的完整系统,主动力有势。
应用哈密顿正则方程
求解,取广义坐标为θ。
系统的功能T 为
)sin (2
122222θωθa a m T += 系统的势能为
θcos mga V =
拉格朗日函数L 为 θθωθcos )sin (2122222mga a a m L -+= 为求哈密顿函数H ,先求广义动量p θ
θθ
θ 2ma L p =∂∂= 哈密顿函数H 为 θθωθθθθθcos sin 2122242222mga a a m p a m ma p p L p H +⎪⎪⎭⎫ ⎝⎛--=-=
正则方程为
θθθθp H p H -=∂∂=∂∂, 得到
θθ =p ma 21 (1) θθθθωp
mga ma -=--sin cos sin 22
(2)
2 由式(1)(2)得到
θ
θθθω 222sin cos sin a ga a -=-- 或者写成
θθθωθsin cos sin 2g a a += 哈密顿函数H 中不显含时间t ,有广义能量积分,即
h g a a '=+-θθωθcos sin 2
121222。


用球坐标写出球摆的哈密顿正则方程泊松括号哈密顿力学一般是指以哈密顿函数为主函数的力学体系。
哈密顿函数一个罗斯函数的一个显然的推广:将朗格朗日力学中的所有的qk,q˙k换成qk,pk即可,事实上,这也正是数学上定义的勒让德变换。
将L中显含的时间t视作参数不参与变换,我们有:dL(qk,q˙k)=∑k∂L∂qkdqk+∑k∂L∂q˙kdq˙k按照动量定义式pk=∂L∂q˙k和拉格朗日方程:p˙k=∂L∂qk带入上面的式子:dL(qk,q˙k)=∑kp˙kdqk+∑kpkdq˙k我们的目标是让上面的式子不含dq˙k,所以利用pkdq˙k=d(pkq˙k)−q˙kdpk带入上面的式子:dL(qk,q˙k)=∑kp˙kdqk+∑kd(pkq˙k)−∑kq˙kdpk简单的合并一下得到:d(∑kpkq˙k−L)=−∑kp˙kdqk+∑kq˙kdpk那么根据全微分的定义,被微分的函数是qk,pk的函数,那么定义H=∑kpkq˙k−L就是很自然的。
对于主函数为H(pk,qk,t),写出它的全微分,有:dH=−∑kp˙kdqk+∑kq˙kdpk所以:∂H∂qk=−p˙k,∂H∂pk=q˙k,左边的方程也称作哈密顿方程,他与前面的拉格朗日-欧拉方程的信息完全一样。
也就是,哈密顿力学给出了力学的另一个表述形式。
启动哈密顿力学有一些绝妙的好处,首先是其上可以定义一个代数(事实上,无歧义来说,代数是指的一个线性代数,而我们这里事实上是一个李代数,如果你没有学过高等代数,请忽略。
)考虑一个力学量,在(pk,qk)张成的空间中,哈密顿已知,为了探讨这个量,我们考虑做他的全微分:df(pk,qk,t)=∑k(∂f∂pkdpk+∂f∂qkdqk)+∂f∂tdt,由于系统的哈密顿已知,系统的全部信息都已经被获取,事实上任何力学量都只依赖于时间,带入哈密顿方程,消去dqk,dpk,得到:dfdt=∂f∂t+∑k(∂f∂qk∂H∂pk−∂f∂pk∂H∂qk),用一些带有启发性的标记标记括号中的内容:dfdt=∂f∂t+∑k∂(H,f)∂(pk,qk),引入泊松括号:{H,f}=∑k∂(H,f)∂(pk,qk)那么dfdt=∂f∂t+∑k∂(H,f)∂(p,q)=∂f∂t+∑k∂(H,f)∂(p,q)=∂f∂t+{H,f}p,q=[∂∂t+{H,⋅}]f那么抽调出“算符”的形式,有:ddt=∂∂t+{H,⋅}回想牛顿力学中,转动参照系的导数,即考虑一个矢量在原参考系的导数和转动参考系的导数,有:dG→dt|fixed=dG→dt|rot+ω→×G→;,抽调成算符:ddt|fixed=ddt|rot+ω→×我们自然的联想到,泊松括号这个二元算符(指有两个量参加运算,如:加法、减法、乘法等),和叉积的相似性。
§6.哈密顿正则方程引言:哈密顿正则方程是与拉氏方程:0=∂∂-∂∂a a q L qL dt d 等价的动力学方程。
s q L q L dt d a a ,....2,10==∂∂-∂α ,这组拉氏方程是s 个关于广义坐标a q 的二阶常微分方程。
在这组拉氏方程中的拉氏函数L 它是广义坐标q ,广义速度q以及时间t 的函数:),,(t qq L L =。
如果我们把拉氏函数中的广义速度a q 变换成→广义动量αp ,即),,(t p q L L =那么就可以将上面的s 个拉氏方程①化成2s 个一阶常微分方程,而且这2s 个一阶常微分方程还具有一定的很漂亮的对称性②具有一定的对称性。
要想把拉氏函数:),,(t qq L L =变成是广义坐标、广义动量P 及时间t 的函数→),,(t p g L L =,以及将s 个拉氏方程化成2s 个一阶常微分方程。
将会用到勒襄特变换这一数学工具。
∴得先介绍一下:一.勒襄特变换(只作了解,不作要求,大纲不要求讲这部分内容)现在先讨论两个变量的勒襄德变换,假设所给的函数是两个变量x 1 和x 2的函数,即:),(21x x f f =。
则由高等数学的知识可得此函数的全微分:2211dx x f dx x f df ∂∂+∂∂=在此我们令11x f u ∂∂=,22x f u ∂∂=,[ii x f u ∂∂=(i=1,2)]……①并以1u 和2u 为新的变量定义一个新函数g: ∑=-+=-≡212211i i if u x u x f u xg ……②如果我们从变换方程①解出i x ,使i x 是i u 的函数,即)(i i i u x x =,再代入上式②中去,那么,g 就是只含新变量i u 的函数了,即:),(21u u g g =。
我们先对②式两边进行微分,则得:∑∑∑∑=====⎥⎦⎤⎢⎣⎡⋅∂∂-+=∂∂-+=21212121)()(i i i i i i i i i i i i i i i i i du x dx x f u du x dx x f dx u du x dg 又∵将旧变量i x 换成新变量i u 之后,新函数g 就是新变量i u 的函数:),(21u u g g =那么对它微分就有:2211du u g du u g dg ∂∂+∂∂=……*′,将这个等式与上一等式进行比较就可得到变换关系:11u g x ∂∂=,222du u g x ∂∂=……③前面我们利用变换方程①把旧的变量x 1,x 2及旧的函数),(21x x f 变为新的变量21,u u 及新的函数),(21u u g g =的方法,就称为勒让德变换。