当前位置：文档之家 › 5.5 哈密顿正则方程

5.5 哈密顿正则方程

  • 格式：ppt
  • 大小：309.00 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

哈密顿正则化

哈密顿正则化

矢量力学：以牛顿运动定律为基础研究力学单个质点所受外力以及由此引起的变化分析力学：力→力的功，动量→动能，着眼于作为整体的力学系统分析力学的变分原理：是矢量力学无数分开的运动微分方程的基础，且与坐标系的选择无关。

约束：加在系统上、限制系统运动的条件；约束力：维持这些约束的力；（分析力学一般不需知道约束力的情况，而径直承认这些约束条件，由这些约束出发得到运动方程）约束可以分为：完整约束（/几何约束）（具有完整约束的力学系统称为完整系统）定常约束非定常约束微分约束将系统内的位置和速度联系在一起非完整约束（具有不可积微分约束的系统称为非完整系统）还可以分为：双面约束：系统可能发生的符合约束的所有位移都是可逆的；用等式表示；单面约束：微小的许可位移是不可逆的；用不等式表示。

实位移：在实际运动中系统各质点的位移；可能位移：符合所有完整约束方程和非完整约束方程的各质点的位移；虚位移：在约束许可的条件下，在某时刻t，想象系统中各质点的位置作任意的、无限小的变更，所形成的位移称为虚位移；虚位移仅仅是一种“探测”，没有时间的改变，故遵从同一时刻t的约束；不同于可能约束；虚位移其实就是约束许可下位置的变分；对单面约束，虚位移不全是可逆的；系统的自由度n=3N-(m+m’)：在约束许可下，各质点的坐标中有3N-(m+m’)个可以独立变化的量，表征系统能“自由”运动的程度。

广义坐标：用q1，q2，…qn表示的、决定系统位形的独立参数称为广义坐标；描述整个系统，一般来自由度为n的完整系统就需要n个独立坐标来描述系统的位形；广义速度：广义坐标对时间的微商。

位形点：将n个数q1，q2，…qn看做n维空间的一个点，这样的点称为位形点；动力学问题的解即表示为系统位形随时间的变化，对应着n维空间的位形点沿一定曲线运动，任意给定时刻都对应着一个位形点。

位形空间：整个力学系统的位形与多维空间中的一个位形点对应，该多维空间称为位形空间。

哈密顿正则方程

哈密顿正则方程

=
V
(r0
)+
∂V ∂r
r0 (r − r0 )
+ 1 ∂2V 2 ∂r 2
r0 (r − r0 )2 + ⋅⋅⋅⋅⋅⋅
r0
r
V
(r)
=
1 2
k
r2
r = r − r0
L
=T
−V
=
1 2
m ( x& 2
+
y& 2
+
z&
2
)
−
1 2
k
r
2
+
1 2
μ (r&2
+
r
2θ& 2
+
r
2ϕ&
2
sin
2
θ
)
L
=T
=
1 ml2θ&2 (1+ cos2 θ ) + mgl sinθ
4
= E0
= mgl
θ& θ = 0 =
2g l
y m1
m1x1 + m2x2 = 0
坐标数 约束数
3 x1 = −x2 2
m2 θ
自由度数 1
x
取如图所示 θ 为广义坐标
yc
=
l 2
sin θ
y
y& c
=
l 2
θ&
cos
θ
yc
根据柯尼西定理
T
=
1 2
2my&c2
+
1 2
I cθ& 2
T = 1 ml2θ&2 (1+ cos2 θ )

哈密顿正则方程课件

哈密顿正则方程课件

解析解的意义
解析解能够精确地描述系统的运 动状态，对于理解和分析物理现 象具有重要意义。
哈密顿正则方程的物理意义
系统能量守恒
哈密顿正则方程描述了系统的能量守恒关系，即系统的总能量保持 不变。
运动状态演化
哈密顿正则方程描述了系统运动状态的演化过程，即随着时间的推 移，系统的运动状态会发生怎样的变化。
广义哈密顿正则方程
广义哈密顿正则方程是经典哈密顿正则方程的扩展，它允许系统具有非保守力和非完整约束。
广义哈密顿正则方程的形式为：$frac{d}{dt}frac{partial L}{partial q'} - frac{partial L}{partial q} = Q$， 其中$L$是系统的拉格朗日函数，$q'$和$q$是系统的广义坐标，$Q$是非保守力。
在统计物理中的应用
描述系统微观状态
哈密顿正则方程在统计物理学中用于描述系统的微观 状态和能量。
分析系统宏观性质
通过哈密顿正则方程，可以分析系统的宏观性质，如 温度、压强和熵等。
研究相变和临界现象
哈密顿正则方程可以用来研究相变和临界现象，包括 对称性破缺和标度律等。
05
CATALOGUE
哈密顿正则方程的扩展与深化
广义哈密顿正则方程在分析力学、动力学和控制系统等领域有广泛应用。
非完整约束系统中的哈密顿正则方程
非完整约束系统是指具有非完整约束的力学系 统，这些约束不能由牛顿第三定律完全确定。
在非完整约束系统中，哈密顿正则方程需要考 虑约束对系统运动的影响，其形式与完整约束 系统中的哈密顿正则方程有所不同。
非完整约束系统中的哈密顿正则方程在机器人 学、航天器和车辆动力学等领域有重要应用。

分析力学第七章正则方程

分析力学第七章正则方程

知 必须满足条件：
由此得出重要推论：
当不显含t时， 为运动常数的充要条件是：
3. 泊松定理
如果函数
和函数
分，则函数[f , g]也是正则方程的初积分。
证：由于是f和g正则方程的初积分，得
是正则方程的两个初积
由雅克比恒等式： 得 于是有 即得到:
因此[f,g]=C也是正则方程的初积分.
泊松定理指出: 由正则方程的两个已知的初积分, 可不断地求出新的初 积分.
那么有
；于是得到：
(即在该四种正则变换中哈密顿量保
持不变).
此时正则变换条件变为下列形式：
。
例1.寻求常数 ,使变换
解：由于此变换不显t，有
是正则变换。
即
, 由于q的任意性，得
因此有变换：
该变换被彭家莱应用于天体力学中
例2. 证明变换 关的四类母函数。 解：
是正则的，并求出与该变换相
因此该变换是正则的。其母函数为：
，其中
是n+1个任意常数。
另外，如果我们已知
，其中
是n+1个任意常数。同样可以得到哈密顿—雅克比偏微
分方程：
——这是哈密顿在当时推证所用的方法。 利用哈密顿—雅克比方程求出
---这样就能得到正则方程的全部积分。
由
及哈密顿正则方程
若力学体系的哈密顿函数H中不显函时间t，即 (h是积分常数)。
；则
当约束又是稳定的，则动能可表示为
2n个代数方程是相互独立的，所以可以解出逆变换为：
若通过变量的变换，使得正则方程的形式保持不变，即：
我们把这种变换叫做正则变换。 当取第二类母函数 则正则变换的条件： 变为：
令
ቤተ መጻሕፍቲ ባይዱ

5.5 哈密顿正则方程ppt课件

5.5 哈密顿正则方程ppt课件

H
H ( p,q,t)
dH dt
s 1
H p
p
H q
q
H t
正则方程
s 1
H p
H q
H q
H p
H t
dH H dt t
H t
若H不显含t, 则H守恒。
8
5.5.3 能量积分与循环积分
循环积分
若H不显含某个广义坐标q ，则根据正则方程
可得：
p
H q
0
p
常数
即相应的广义动量守恒。
16
5.5 哈密顿正则方程
分析：四、最终的运动微分方程
例题 2
由(5')(8')可得
p mr2 h(常数)
(11)
即在垂直于运动平面方向上的动量矩守恒。
对(11)求导即得到横向运动微分方程。
由(4')(7')(11)可得
m(r
r2 )
r2
(12)
即径向运动微分方程
17
5.5 哈密顿正则方程
18
(1)(2)联立可得
x k x 0 m
即一维弹簧振子的 运动微分方程
11
5.5 哈密顿正则方程
例题 2
例 2 用哈密顿正则方程建立质点在有心力势场
V
(r)
r
中的运动微分方程.
解：采用球坐标 (r, ,) 描述 位矢 r rer
质点的速度
v
d dt
(rer
)
rer
re
r sine
拉氏函数 L T V 1 m(r2 r22 r2 sin2 2 )
注：这里的能量积分与循环积分，与从拉氏函数得到的 能量积分和循环积分，结果是一样的。

哈密顿力学

哈密顿力学

哈密顿力学哈密尔顿力学是哈密尔顿于1833年建立的经典力学的重新表述。

它由拉格朗日力学演变而来，那是经典力学的另一表述，由拉格朗日于1788年建立。

但它可以使用辛空间不依赖于拉格朗日力学表述。

关于这点请参看其数学表述。

哈密顿力学-简介哈密顿力学是标准的“伽利略加速点运动几何学”的一种力学。

不幸的是，后人将其称作是“新几何力学”，这多多少少显示了后人的数学知识和物理学思想的一种令人遗憾的欠缺。

哈密顿系统可以理解为时间R上的一个纤维丛E,其纤维Et,t∈R是位置空间。

拉格朗日量则是E上的jet丛(射流丛)J上的函数；取拉格朗日量的纤维内的勒让德变换就产生了一个时间上的对偶丛的函数，其在t 的纤维是余切空间T*Et，它有一个自然的辛形式，而这个函数就是哈密顿量。

任何辛流形上的光滑实值函数H可以用来定义一个哈密顿系统。

函数H称为哈密顿量或者能量函数。

该辛流形则称为相空间。

哈密顿量在辛流形上导出一个特殊的向量场，称为辛向量场。

该辛向量场，称为哈密顿向量场，导出一个流形上的哈密顿流。

该向量场的一个积分曲线是一个流形的变换的单参数族；该曲线的参数通常称为时间。

该时间的演变由辛同胚给出。

根据刘维尔定理每个辛同胚保持相空间的体积形式不变。

由哈密顿流到处的辛同胚的族通常称为哈密顿系统的哈密顿力学。

哈密顿向量场也导出一个特殊的操作，泊松括号。

泊松括号作用于辛流形上的函数，给了流形上的函数空间一个李代数的结构。

当余度量是退化的时，它不是可逆的。

在这个情况下，这不是一个黎曼流形，因为它没有一个度量。

但是，哈密顿量依然存在。

这个情况下，在流形Q的每一点q余度量是退化的，因此余度量的阶小于流行Q的维度，因而是一个亚黎曼流形。

这种情况下的哈密顿量称为亚黎曼哈密顿量。

每个这样的哈密顿量唯一的决定余度量，反过来也是一样。

这意味着每个亚黎曼流形由其亚黎曼哈密顿量唯一的决定，而其逆命题也为真：每个亚黎曼流形有唯一的亚黎曼哈密顿量。

亚黎曼测地线的存在性由Chow-Rashevskii定理给出。

哈密顿正则方程


/ 2m
m
x
2
由正则方程，得 x＝ H p p / m， p － H x m
2
x
由 上 两 式 削 去 p， 得 x 积分，得
2
x 0
x A c o s ( t ) p － m A s in ( t )
表明谐振子的相轨道为沿顺时针方向的 封闭椭圆。 物理与光电工程学院
第五章 分析力学
§5.5 哈密顿正则方程
知识回顾 • 基本形式的拉氏方程
d T d t q T q Q
• 保守系的拉氏方程
d L d t q L q 0
• 拉氏方程的应用
a. 确定自由度 b. 选取广义坐标 c. 写出体系的拉氏函数 d. 解拉氏方程并讨论
2 2
由 定 义 求 p ， 并 进 而 求 哈 密 顿 函 数 H : L ， p L m r 2 sin 2 pr m r， p m r r p 1 m ( r 2 r 2 2 r 2 sin 2 2 ) H L p r r p 2 r 1 2 m ( pr
g
二、正则方程
y
v,
g u

x
（正则形式）
前面提过，用 P代换L函数的 q有一定的优越性， q P 但只用 代换 而不改变函数的形式，则原函数 对新变量无正则形式，给计算带来麻烦.

下面把L函数: L ( q , q , t ) 和 f ( x , y ) 比较
a o
5 g sin ( R r ) 7
19
物理与光电工程学院

2023大学_理论力学教程第三版(周衍柏著)课后答案下载

2023理论力学教程第三版(周衍柏著)课后答案下载理论力学教程第三版内容简介绪论第一章质点力学1.1 运动的描述方法1.2 速度、加速度的分量表示式1.3 平动参考系1.4 质点运动定律1.5 质点运动微分方程1.6 非惯性系动力学(一)1.7 功与能1.8 质点动力学的基本定理与基本守恒定律1.9 有心力小结补充例题思考题习题第二章质点组力学2.1 质点组2.2 动量定理与动量守恒定律2.3 动量矩定理与动量矩守恒定律 2.4 动能定理与机械能守恒定律 2.5 两体问题2.6 质心坐标系与实验室坐标系 2.7 变质量物体的运动2.8 位力定理小结补充例题思考题习题第三章刚体力学3.1 刚体运动的分析3.2 角速度矢量3.3 欧拉角3.4 刚体运动方程与平衡方程3.5 转动惯量3.6 刚体的平动与绕固定轴的.转动 3.7 刚体的平面平行运动3.8 刚体绕固定点的转动__3.9 重刚体绕固定点转动的解__3.10 拉莫尔进动小结补充例题思考题习题第四章转动参考系4.1 平面转动参考系4.2 空间转动参考系4.3 非惯性系动力学(二)__4.5 傅科摆小结补充例题思考题习题第五章分析力学5.1 约束与广义坐标5.2 虚功原理5.3 拉格朗日方程5.4 小振动5.5 哈密顿正则方程5.6 泊松括号与泊松定理5.7 哈密顿原理5.8 正则变换__5.9 哈密顿-雅可比理论__5.10 相积分与角变数__5.11 刘维尔定理小结补充例题思考题习题附录主要参考书目理论力学教程第三版目录本书是在第二版的基础上修订而成的，适用于高等学校物理类专业的理论力学课程。

本书与第二版相比内容保持不变，仅将科学名词、物理量符号等按照国家标准和规范作了更新。

本书内容包括质点力学、质点组力学、刚体力学、转动参考系及分析力学等，每章附有小结、补充例题、思考题及习题。

分析力学基础(9)


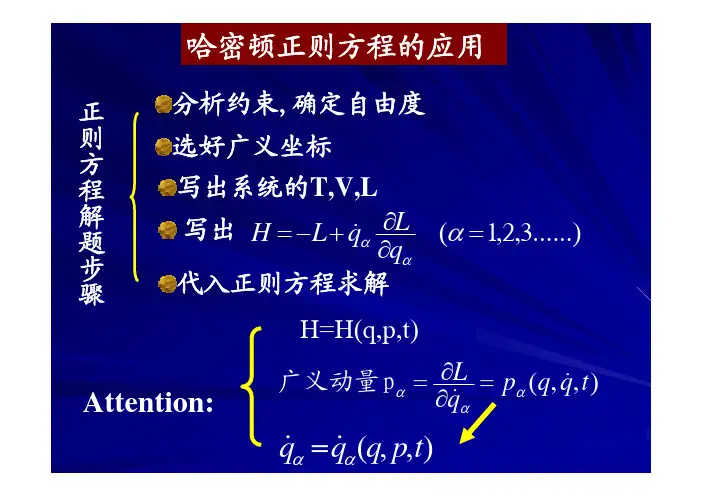
哈密顿正则方程——广义坐标和广义 哈密顿正则方程——广义坐标和广义 动量的一阶微分方程组
哈密顿正则方程
哈密顿函数
系统的拉格朗日函数和广义动量分别是
ɺ ɺ ɺ L = L(q1, q2 ,⋯qN ; q1, q2 ,⋯qN ;t)
∂L ɺ ɺ ɺ pi = = pi (q1, q2 ,⋯qN ; q1, q2 ,⋯qN ; t), (i =1 2,…, N) , ɺ ∂qi
拉格朗日方程可写成
d pi ∂L = dt ∂qi
(i =1 2,…, N) ,
从广义动量方程中解出广义速度， 从广义动量方程中解出广义速度，它是广义坐标和广 义动量的函数， 义动量的函数，即
哈密顿正则方程
ɺ ɺ qi = qi (q1, q2 ,⋯qN ; p1, p2 ,⋯pN ;t), (i =1 2,…, N) ,
不含时间 t，所以有广义能量积分
p2 k 2 + q = E(常数 ) 2m 2
哈密顿正则方程
例 题 3 y m
θ
半径为 a 的圆环以匀角速度 ω 绕 O 轴在水 平面内运动，环上有一质量为m的质点。 平面内运动，环上有一质量为m的质点。写出 质点的哈密顿正则方程及其首次积分 解：拉格朗日函数为
L =T = m 2 m ɺ ɺ ɺ ɺ (x + y2 ) = a2θ 2 + ma2ω(θ +ω)(1+ cosθ ) 2 2
~ q(t) = q(t) +δq(t) = q(t) +αη(t)
其中η(t)的定义域是[t0, t1]，且η(t0) = η(t1) = 0 的定义域是[ 这个集合称为函数 这个集合称为函数q(t)的“邻域” 函数q 邻域”

哈密顿力学


§5-3 正则方程
1.从拉格朗日方程到正则方程
统计物理、电动力学和量子力学等理论物理学科中对力学的 描述更多的是采用哈密顿正则方程的形式。
根据哈密顿函数的定义
d H d L s p q & s(q & a d p a p a d q & a ) d L
1
a 1
d dt q & L q L =0
d dx
f y
'
f y
0
欧勒方程
例：求最速落径方程
解：已知
f
1 y '2 ， 2gy
根据欧勒方程
d f
dx
y
-
f 0. y
f 1 1 y '2 y 3 / 2 ; f 1 (1 y '2 ) 1/ 2 y
y 2 2g
y 2gy
d
dx
1 2gy
(1
y
'2 ) 1/ 2
Q qt1 qt2 0
t1 t2s1qL d dtq & L qdt0
Qq 是 任 意 的
d dt q & L q L 0
(1,2...s)
三. 哈密顿原理的意义
➢哈密顿原理在理论上具有特别重要的意义, 它是建立在描述 体系运动总体效果----积分形式的基础之上，与采用什么样的 广义坐标（坐标系）无关，因此只要适当引进拉格朗日函数 （对相互作用需要建立模型得到势函数或力函数，进而得到拉 格朗日函数）,就容易推广应用拉格朗日方程和正则方程,并建 立整个分析力学的体系.
T [ y ( x ) ] x2 f ( y , y ', x ) d x 可 以 证 明 泛 函 T [ y ( x ) ] 取 极 值 的 条 件 是 其 x1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

正则方程
H H H H p q q p 1
s
H t
dH H dt t
H t
若H不显含t, 则H守恒。
8
5.5.3 能量积分与循环积分
循环积分 若H不显含某个广义坐标 q ，则根据正则方程 可得： H
H pr r pr m p H 2 p m r p H 2 2 p m r sin
(2) (3)
2 p H p2 r 3 3 2 2 p r m r m r sin r 2 p H cos p 2 3 m r sin H p 0
(4) (5)
(7) (8)
(6)
(9)
13
5.5 哈密顿正则方程
例题 2
分析：一、动量矩守恒
C(常数) 由(6)(9)可得 p mr2 sin2
(10)
另一方面计算可得 J z (r mv) e z mr2 sin 2
可见(10)代表沿z方向的动量矩守恒。 但是z轴的方向是任意选择的，故沿任何方向都 有动量矩守恒，从而系统动量矩守恒，即
O
这意味着质点将始终保持在z轴和初位 矢r0所确定的平面内运动。 z轴就是平面极坐标的极轴。
15
5.5 哈密顿正则方程
例题 2
H pr r pr m p H 2 p m r p H 2 2 p m r sin
1 2 动能 T mx 2
平衡位置
m
O
光滑水平面
x
弹簧劲度系数为k
1 2 势能 V kx 2
拉氏函数
1 2 1 2 kx L T V mx 2 2
L 广义动量 p x mx x
px x m
10
5.5 哈密顿正则方程
例题 1
哈密顿函数
Lx H px x p
5.5 哈密顿正则方程
5.5.1 勒让德变换
哈密顿函数的定义式
1, q 2 ,...,q s ; t ) 拉氏函数 L L(q1, q2 ,...,qs ; q
(1) (2) (3)
广义动量
L 1, q 2 ,...,q s ; t ) p p (q1, q2 ,...,qs ; q q
s
L H p q
1
规则：
)乘以原函数(L)对该变量的 把要消去的变量(q )后，再减去原函数。 偏导( p L q
4
5.5.2 正则方程
正则方程的推导
L dH ( p dq q dp ) dL H p q
2 m( r r ) 2 r
(12)
即径向运动微分方程
17
5.5 哈密顿正则方程
18
1 1
s s
(1)
L L L , t ) dL L L(q, q dq dt q dq q 1 t
s
L dq p dq ) ( p dt t 1
s
(2)
12
5.5 哈密顿正则方程
例题 2
哈密顿量
正则方程
1 2 2 2 2 2 2 ) r r sin H T V m( r 2 r 2 2 p 1 p 2 p (1)代入(2)可得 H r 2 2 r 2m r r sin
p q 0 p 常数
即相应的广义动量守恒。
注：这里的能量积分与循环积分，与从拉氏函数得到的 能量积分和循环积分，结果是一样的。
9
5.5 哈密顿正则方程
例题 1
例1 试用哈密顿正则方程建立图示一维弹簧振子的 运动微分方程。 解：以平衡位置(即 弹簧原长位置)为原 点，建立一维x轴。
q ( p1, p2 ,..., ps ; q1, q2 ,...,qs ; t ) 由(2)解得 q
定义另外一个函数，称为哈密顿函数
H H ( p1, p2 ,..., ps ; q1, q2 ,...,qs ; t )
L p q
1
s
要 其中的 q 用(3)代换。
(7) (8) (9)
p2 r 3 2 p mr r p 0
(4')
(7')
(8')
16
(5')
5.5 哈密顿正则方程
例题 2
分析：四、最终的运动微分方程 由(5')(8')可得
h(常数) p mr
2
(11)
即在垂直于运动平面方向上的动量矩守恒。 对(11)求导即得到横向运动微分方程。 由(4')(7')(11)可得
2
5.5.1 勒让德变换
哈密顿函数的物理含义
L 常数 若L不显含t, 则 H p q
1
s
对于稳定约束系统，H即系统总能量
H T V
对于不稳定约束系统，H是广义能量
H T2 T0 V
3
5.5.1 勒让德变换
勒让德变换的规则
, t ) 到变换。 以上从 L(q, q
(2)代入(1)可得
L dp p dq ) dt dH (q t 1
s
(3)
5
5.5.2 正则方程
s
正则方程的推导
L dp p dq ) dt dH (q t 1
(3)
另一方面
H H H H H ( p, q, t ) dH p dp q dq t dt 1
相空间的一点，代表系统可能存在的一个状态， 称为相点。 随时间变化，相点在相空间移动，划出一条曲 线，代表系统状态的演化路径。
7
5.5.3 能量积分与循环积分
能量积分
s H dH H H H H ( p, q, t ) p q dt 1 p q t
即一维弹簧振子的 运动微分方程
11
5.5 哈密顿正则方程
例题 2
例 2 用哈密顿正则方程建立质点在有心力势场 V ( r ) 中的运动微分方程. r 解：采用球坐标 (r, , ) 描述 位矢 r rer
d e r sin e er r 质点的速度 v (rer ) r dt 1 2 2 2 2 2 2 r r sin ) 拉氏函数 L T V m( r 2 r p L r r mr 广 pr r m 义 L p 2 p m r (1) 2 动 mr p 量 p L m r2 sin 2 m r2 sin 2
r pr m p m r2
分析：三、简化正则方程
2 p H p2 r 3 3 2 2 (4) p r m r m r sin r 2 p H cos p (5) 2 3 m r sin H (6) p 0 0, p 0
x
正则方程
m
2
px 1 px 1 2 px m kx m 2 m 2
p 1 2 kx 2m 2
2 x
H px x px m H p x kx x
(1) (2)
(1)(2)联立可得
k x 0 x m
s
(4)
(3)(4)比较可得哈密顿正则方程
H q p H p q
以及
,
H L t t
1, 2,...,s
若L不显含t, 则H也 不显含t.
6
5.5.2 正则方程
相空间 s个广义坐标，和s个广义动量，统称为正则变量， 它们作为相互独立的变量，张开一个2s维空间， 称为相空间。
J C (常矢量)
14
5.5 哈密顿正则方程
例题 2
分析：二、平面运动 现在选择一个特殊的z轴方向：使初速度v0躺在z 轴和初位矢r0所确定的平面内。
z
v0
r0
er
e
C(常数) p mr2 sin 2
(10)
则根据(10)式，可得初始时刻，以 及后面任意时刻，都有
0, C 0, p 0