下载文档原格式
哈密顿力学和正则方程的研究哈密顿力学是理论物理中的一个重要分支，主要用于描述和研究力学系统。
它是由物理学家威廉·哈密顿提出的，并以他的名字命名。
哈密顿力学的核心是哈密顿原理，它提供了确定力学系统演化的数学框架。
本文将探讨哈密顿力学以及与之相关的正则方程，以及它们在物理学中的应用。
1. 哈密顿力学的基本概念哈密顿力学是经典力学的一个重要分支，它在描述动力学系统时使用了一种不同的数学表述。
与拉格朗日力学相比，哈密顿力学更侧重于系统的相空间，并使用广义坐标和广义动量来描述系统状态。
在哈密顿力学中，系统的状态可以用哈密顿函数来描述，而力学系统的演化则由哈密顿方程来控制。
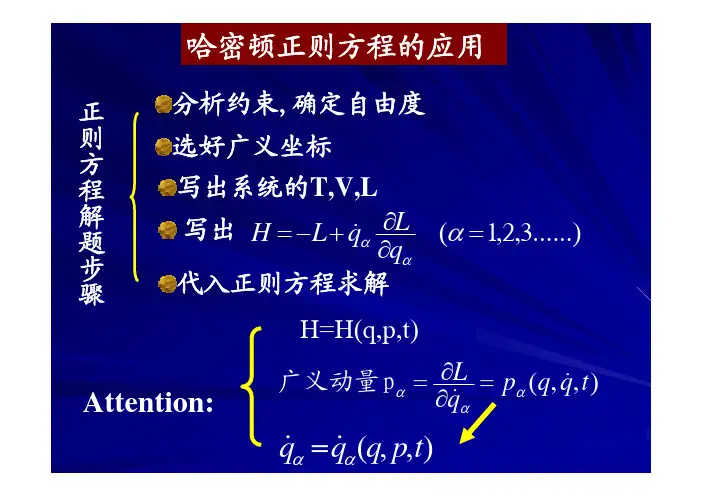
2. 正则方程的推导与应用正则方程是哈密顿力学中非常重要的一个概念，它描述了系统的演化方式。
正则方程可以通过应用哈密顿原理来推导得到，通过对哈密顿函数求极值，可以得到系统的正则方程。
这些方程描述了系统在相空间中的运动轨迹，从而提供了对系统演化的详细描述。
3. 哈密顿力学在量子力学中的应用除了在经典力学中的应用，哈密顿力学在量子力学的研究中也起到了重要的作用。
量子力学中的哈密顿力学描述了量子系统的演化，诸如自旋、波函数等可以用哈密顿算子来描述。
通过计算哈密顿算子的本征值和本征函数，可以得到量子系统的能量谱和态函数。
4. 哈密顿力学在天体力学中的应用哈密顿力学在天体力学中也有广泛的应用，尤其是在描述行星、卫星、恒星等天体的运动时。
通过建立天体系统的哈密顿函数，并求解对应的正则方程，可以得到天体的运动轨迹和动力学特性。
这对于理解宇宙中的天体运动以及探索行星航天等领域都具有重要意义。
5. 哈密顿力学与量子力学的统计解释此外，哈密顿力学还有与量子力学的统计解释相关的研究。
通过应用配分函数和统计力学的方法，可以从经典的哈密顿力学出发，推导出量子力学中的统计物理量。
这为理解量子系统的统计行为提供了一个重要的框架，并在凝聚态物理和粒子物理等领域发挥了重要作用。
哈密顿正则方程使用条件嘿，朋友们！今天咱们来唠唠哈密顿正则方程的使用条件，这就像是一场神秘的魔法，只有满足特定条件才能施展呢！首先呢，咱得在保守力系的魔法世界里。
保守力系就像那种特别靠谱、守规矩的老管家，不管怎么折腾，它总有个稳定的能量储存方式。
你看啊，就像重力，你把东西举高了，它就像攒着一股劲儿，随时准备把东西拉下来，能量可不会凭空消失或者冒出来。
这时候哈密顿正则方程就像个乖巧的小精灵，在这个稳定的保守力系环境里开始欢快地跳舞，方程$H =T+V$（这里$H$是哈密顿函数，$T$是动能，$V$是势能）就能大显身手啦。
然后呢，系统的自由度得是有限个。
这就好比一场聚会，人数要是多得没边儿了，那可就乱套了，根本没法好好管理。
如果自由度无限多，就像有无数个调皮捣蛋的小猴子在乱窜，哈密顿正则方程这个指挥家可就头疼得没法指挥了。
只有自由度有限，就像一个小乐队，每个乐器（自由度）都有数，那方程就能把每个乐器的节奏（运动状态）安排得明明白白。
再说说坐标的选取。
这坐标就像是探险的地图，得选得恰到好处。
要是选错了坐标，就像拿着一张错误的地图在迷宫里乱转。
你以为你在朝着宝藏（正确的解）前进，其实越走越偏。
只有选取合适的广义坐标，比如说在研究单摆的时候，选取摆角作为广义坐标，这样哈密顿正则方程这个指南针才能准确地指向正确的方向，带着我们找到物理问题的答案。
还有啊，系统得是完整约束系统。
完整约束就像是给系统穿上了合身的衣服，虽然有点约束，但还能活动自如。
如果是不完整约束，那就像是穿了一身到处是铁链子的奇怪衣服，行动都困难，哈密顿正则方程这个小机灵鬼在这种情况下就会被束缚住手脚，根本没法施展它的本事。
另外呢，相空间得是定义良好的。
相空间就像一个超级大舞台，每个粒子的位置和动量就是舞台上演员的坐标。
要是这个舞台乱七八糟，一会儿大一会儿小，那演员（粒子）可就没法好好表演了。
只有相空间稳定、明确，哈密顿正则方程这个导演才能有条不紊地指挥这场物理大戏。
