第7章 明渠非均匀流.
- 格式:doc
- 大小:4.54 MB
- 文档页数:17


第七章明渠流【教学基本要求】1、了解明槽水流的分类和特征,了解棱柱体渠道的概念,掌握明槽底坡的概念和梯形断面明渠的几何特征和水力要素。
2、了解明槽均匀流的特点和形成条件,熟练掌握明槽均匀流公式,并能应用它来进行明渠均匀流水力计算。
3、理解水力最佳断面和允许流速的概念,掌握水力最佳断面的条件和允许流速的确定方法,学会正确选择明渠的糙率n值。
4、掌握明槽均匀流水力设计的类型和计算方法,能进行过流能力和正常水深的计算,能设计渠道的断面尺寸。
5、掌握明渠水流三种流态(急流、缓流、临界流)的运动特征和判别明渠水流流态的方法,理解佛汝德数Fr的物理意义。
6、理解断面比能、临界水深、临界底坡的概念和特性,掌握矩形断面明渠临界水深h k 的计算公式和其它形状断面临界水深的计算方法。
7、了解水跃和水跌现象,掌握共轭水深的计算,特别是矩形断明渠面共轭水深计算。
8、能进行水跃能量损失和水跃长度的计算。
9、掌握棱柱体渠道水面曲线的分类、分区和变化规律,能正确进行水面线定性分析,了解水面线衔接的控制条件。
10、能进行水面线定量计算。
【学习重点】• 1. 明渠均匀流水力计算;• 2. 明渠水流三种流态的判别;• 3. 明渠恒定非均匀渐变流水面曲线分析和计算,这部分也是本章的难点;• 4. 水跃的特性。
【内容提要和学习指导】这一章是工程水力学部分内容最丰富也是实际应用最广泛的一章。
本章有4个重点:明渠均匀流水力计算;明渠水流三种流态的判别;明渠恒定非均匀渐变流水面曲线分析和计算,这部分也是本章的难点;水跃的特性和共轭水深计算。
学习中应围绕这4个重点,掌握相关的基本概念和计算公式。
§7-1 概 述人工渠道,天然河道及水流未充满全断面的管道等统称为明渠。
明渠水流是一种具有自由液面的水流,水流的表面压强为大气压强,即相对压强为零。
因此,明渠水流也称为无压流,而管流中的水流充满全断面,没有自由表面。
在研究明渠水流运动规律之前,必须对明渠的几何特性有所了解。


第七章明渠恒定非均匀流第一节概述第二节明渠水流的流态及其判别一、急流、缓流的运动学分析缓流:河流中有些水面宽阔的地方底坡平坦,水流缓慢当水流遇有障碍时(如大石头)急流:在河流有些水面狭窄的地方底坡陡峻,且水流湍急将一块石子投入静水中,四周扩散(v + v w),向上游传播的绝对速度为(v w-当水流的流速等于波速(v= v w)时,微波向下游传播的绝对速度是2 v w。
当水流流速大于波速(v > v w )时,微波只向投石点下游传播,对上游的流动没有影响。
明渠流态:缓 流 v < v w ; 临界流 v = v w ; 急 流 v > v w 式中,v 为水流速度,vw 为微波(扰动波)波速判断明渠水流流态必须已知水流速度、微波(扰动)波速;如何考虑微波(扰动)波速?(一) 明渠中微波传播的相对波速一平底矩形断面水渠,水体静止,水深为h ,水中有一个直立的平板。
用直立平板向左拨动一下,板左边水面激起一微小波动,波高∆h ,波以速度v w 从右向左传播。
观察微波传播: 波形所到之处将带动水流运动,流速随时间变化,是非恒定流,但可化为恒定流。
选动坐标随波峰运动,假想随波前进来观察渠中水流相对于动坐标系 波静止渠中原静止水体以波速v w 从左向右流动,整个水体 等速度向右运动,水流为恒定流,水深 沿程变化,是非均匀流。
断面2:波峰处断面1:未受波影响忽略能量损失,由连续方程和能量方程 得 能量方程:()gvh h gvh w2Δ222121αα++=+连续方程:()w Bhv v h h B =+2 Δ式中,B 为水面宽 由此得 ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=h h h h gh v w 2Δ1/Δ1对于波高 Δh << h 的波—小波 h g v w =v式中:B A h =,断面平均水深,A 为过水断面面积,B 为水面宽度 顺水波:h g v v v v w w +=+=' (微波传播方向和水流方向一致) 式中,'w v 顺水波传播波速。

《水力学》形考任务第7章明渠恒定非均匀流一、单选题(共6题,每题5分,共30分)1.判别明渠水流流态的依据是弗汝德数,当Fr>1则为()。
A. 急变流B. 缓流C. 急流D. 临界流正确答案是:急流2.弗汝德数Fr是判别下列哪种流态的重要的无量纲数()。
A. 层流和紊流B. 恒定流和非恒定流C. 均匀流和非均匀流D. 急流和缓流正确答案是:急流和缓流3.明渠非均匀流根据其流线不平行和弯曲的程度,又可以分为()。
A. 急流和缓流B. 恒定流和非恒定流C. 临界流和缓流D. 渐变流和急变流正确答案是:渐变流和急变流4.在缓坡明渠中不可以发生的流动是()。
A. 均匀急流B. 非均匀缓流C. 非均匀急流D. 均匀缓流正确答案是:均匀急流5.共轭水深是指()。
A. 水跃的跃前水深与跃后水深B. 临界水C. 均匀流水深D. 溢流坝下游水流收缩断面水深正确答案是:水跃的跃前水深与跃后水深6.在明渠渐变流中()。
A. 水面线与底坡线平行B. 总水头线与自由水面相重合C. 总水头线一定平行于底坡线D. 测压管水头线与自由水面一致正确答案是:测压管水头线与自由水面一致二、多选题(共2题,每题10分,共20分)7.明渠水流的三种流态有()。
A. 急流B. 缓流C. 均匀流D. 临界流正确答案是:缓流, 急流, 临界流8.明渠水流的判别方法及标准有()。
A. 临界水深:缓流,临界流,急流。
B. 弗汝德数:弗汝德数Fr=,Fr=1临界流,Fr<1 缓流,Fr>1 急流。
C. 临界底坡:缓流,临界流,急流。
D. 干扰波:波速C=,=C为临界流,<c为缓流,>c为急流。
正确答案是:干扰波:波速C=,=C为临界流,<c为缓流,>c为急流。
, 弗汝德数:弗汝德数Fr=,Fr=1临界流,Fr<1 缓流,Fr>1 急流。
, 临界水深:缓流,临界流,急流。
, 临界底坡:缓流,临界流,急流。
明渠恒定均匀流和非均匀流概述1.1 明渠的分类由于过水断面形状、尺寸与底坡的变化对明渠水流运动有重要影响,因此在水力学中把明渠分为以下类型。
(1) 棱柱形渠道和非棱柱形渠道凡是断面形状及尺寸沿程不变的长直渠道,称为棱柱形渠道,否则为非棱柱形渠道。
前者的过水断面面积A 仅随水深h 变化,即A =f (h );后者的过水断面面积不仅随水深变化,而且还随着各断面的沿程位置而变化。
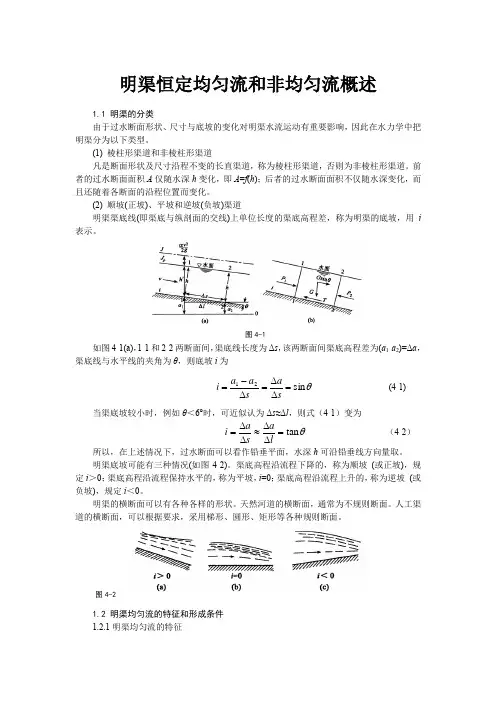
(2) 顺坡(正坡)、平坡和逆坡(负坡)渠道明渠渠底线(即渠底与纵剖面的交线)上单位长度的渠底高程差,称为明渠的底坡,用i 表示。
图4-1如图4-1(a),1-1和2-2两断面间,渠底线长度为Δs ,该两断面间渠底高程差为(a 1-a 2)=Δa ,渠底线与水平线的夹角为θ,则底坡i 为θsin 21=∆∆=∆-=sa s a a i (4-1) 当渠底坡较小时,例如θ<6°时,可近似认为Δs ≈Δl ,则式(4-1)变为 θtan =∆∆≈∆∆=la s a i (4-2) 所以,在上述情况下,过水断面可以看作铅垂平面,水深h 可沿铅垂线方向量取。
明渠底坡可能有三种情况(如图4-2)。
渠底高程沿流程下降的,称为顺坡 (或正坡),规定i >0;渠底高程沿流程保持水平的,称为平坡,i =0;渠底高程沿流程上升的,称为逆坡 (或负坡),规定i <0。
明渠的横断面可以有各种各样的形状。
天然河道的横断面,通常为不规则断面。
人工渠道的横断面,可以根据要求,采用梯形、圆形、矩形等各种规则断面。
图4-21.2 明渠均匀流的特征和形成条件1.2.1明渠均匀流的特征明渠均匀流有下列特性:(1) 过水断面的形状和尺寸、流速分布、水深,沿流程都不变;(2) 总水头线、测压管水头线(在明渠水流中,就是水面线)和渠底线三者为相互平行的直线(图4-1a),因而它们的坡度相等,即J=J p=i(4-3)1.2.2明渠均匀流的形成条件对明渠恒定均匀流,图4-1(b),取1-1、2-2断面之间的水体作为研究对象,分析这块水体上的受力,并沿流向写动力平衡方程为P1-P2+G sinθ-T=0式中P1和P2为1-1和2-2过水断面的动水压力,G为Δs流段水体重量,T为边壁(包括岸壁和渠底)阻力。

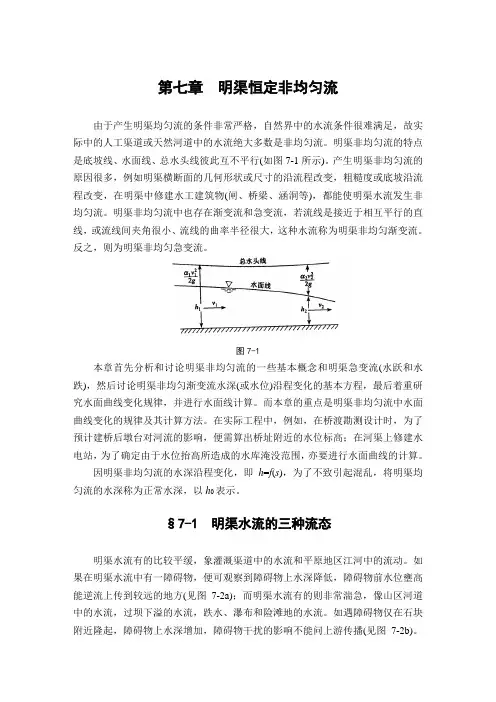
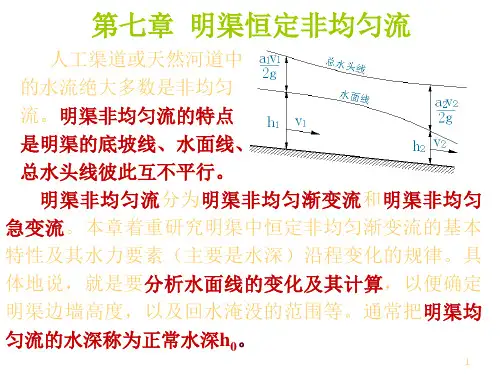
第七章明渠恒定非均匀流由于产生明渠均匀流的条件非常严格,自然界中的水流条件很难满足,故实际中的人工渠道或天然河道中的水流绝大多数是非均匀流。
明渠非均匀流的特点是底坡线、水面线、总水头线彼此互不平行(如图7-1所示)。
产生明渠非均匀流的原因很多,例如明渠横断面的几何形状或尺寸的沿流程改变,粗糙度或底坡沿流程改变,在明渠中修建水工建筑物(闸、桥梁、涵洞等),都能使明渠水流发生非均匀流。
明渠非均匀流中也存在渐变流和急变流,若流线是接近于相互平行的直线,或流线间夹角很小、流线的曲率半径很大,这种水流称为明渠非均匀渐变流。
反之,则为明渠非均匀急变流。
图7-1本章首先分析和讨论明渠非均匀流的一些基本概念和明渠急变流(水跃和水跌),然后讨论明渠非均匀渐变流水深(或水位)沿程变化的基本方程,最后着重研究水面曲线变化规律,并进行水面线计算。
而本章的重点是明渠非均匀流中水面曲线变化的规律及其计算方法。
在实际工程中,例如,在桥渡勘测设计时,为了预计建桥后墩台对河流的影响,便需算出桥址附近的水位标高;在河渠上修建水电站,为了确定由于水位抬高所造成的水库淹没范围,亦要进行水面曲线的计算。
因明渠非均匀流的水深沿程变化,即h=f(s),为了不致引起混乱,将明渠均匀流的水深称为正常水深,以h0表示。
§7-1 明渠水流的三种流态明渠水流有的比较平缓,象灌溉渠道中的水流和平原地区江河中的流动。
如果在明渠水流中有一障碍物,便可观察到障碍物上水深降低,障碍物前水位壅高能逆流上传到较远的地方(见图7-2a);而明渠水流有的则非常湍急,像山区河道中的水流,过坝下溢的水流,跌水、瀑布和险滩地的水流。
如遇障碍物仅在石块附近隆起,障碍物上水深增加,障碍物干扰的影响不能问上游传播(见图7-2b)。
上述两种情况表明,明渠水流存在两种不同的流态。
它们对于所产生的干扰波(Disturbance Wave)的传播,有着不同的影响。
障碍物的存在可视为对水流发生的干扰,下面分析干扰波在明渠中传播的特点。

明渠非均匀流计算公式
明渠非均匀流是指在明渠水流中,由于底坡、流量、水深等因素的变化,导致流速分布不均匀,水力要素(如水深、流速、压强等)沿程发生变化的流动。
这种流动状态在水力学中是很常见的,特别是在天然河流和人工渠道中。
明渠非均匀流的计算公式主要是用来描述这种流动的水力要素沿流程的变化规律。
这些公式通常基于水力学的基本原理,如伯努利方程、连续性方程等,并结合明渠的具体条件进行推导。
下面给出两个明渠非均匀流的计算公式示例:
1.水深沿程变化公式:
2.当明渠中的水流受到阻力作用时,水深会沿流程减小。
这个变化可以用以
下公式描述:
3.$\frac{dh}{dx} = -\frac{Q}{A}\left(\frac{1}{\sqrt{1+S^2}} +
\frac{f}{1+S}\right)$
4.其中,$h$ 是水深,$Q$ 是流量,$A$ 是过水面积,$S$ 是底坡,$f$ 是
阻力系数。
这个公式可以帮助我们了解水流的水深如何随着流程而变化。
5.断面平均流速公式:
6.在明渠非均匀流中,断面平均流速是重要的水力要素。
这个量可以用以下
公式计算:
7.$\bar{v} = \sqrt{\frac{Q}{\pi r^2 h}}$
8.其中,$\bar{v}$ 是断面平均流速,$r$ 是水力半径(即过水面积与湿周之
比),$h$ 是水深。
这个公式可以帮助我们了解水流的速度是如何分布的。
以上两个公式只是明渠非均匀流计算中的一部分,实际上还有许多其他的公式和模型可以用来描述这种流动。
这些公式和模型的选择取决于具体问题的条件和要求。
第七章明渠非均匀流目的要求:掌握非均匀流中比能、临界水深的基本概念;急流、缓流、临界流的判别;水跃的基本概念及共轭水深的计算;12种水面曲线的基本型式及水面曲线的联接;水面曲线的定量计算。
重点:三种流态的判别方法;正常水深、临界水深、共轭水深的计算方法及水跃的三种位置;各种情况下水面曲线的联接;分段求和法计算水面曲线。
难点:各种情况下水面曲线的联接。
§7-1概述一、明渠非均匀流的产生不满足明渠均匀流产生条件的水流为非均匀流。
例如:二、明渠非均匀流的特性用一句话概括:总水头线、测压管水头线、底坡线互不平行,水面线为曲线。
三、主要研究的问题上支0>dh de ,增函数,下支0<dhde ,减函数。
(2)k h h e e h he =→=min 21临界水深二、临界水深h k1、定义:当Q 、断面形状尺寸一定时,断面比能最小值对应的水深叫临界水深。
2、h k 的计算0112323222=-=-=+=ωαωωαωαg B Q dh d g Q dh de g Q h ekkB gQ 32ωα=——临界水深普遍公式(1)任意形状断面解一元高次方程的问题,采用试算图解法 设→→Bh 3ω曲线(2)矩形断面设底宽=b ,B k =b ,k k bh =ωb h b g Q k 332=α ,g q gb Q h k 2223αα==∴,q b Q =——单宽流量 s m 2 32gq h k α=三、临界坡度i k1、定义:在棱柱形渠道中,断面形状、尺寸和流量一定时,若水流的正常水深恰好等于临界水深k h 时,对应的底坡叫临界底坡。
2、k i 的计算由定义,k h 需满足k k k k k kkk k k B C g i B g Q i R C Q 232αχωαω=→⎪⎩⎪⎨⎧== 3、缓坡、陡坡由实际底坡i 和k i 的关系⎪⎪⎩⎪⎪⎨⎧==<>><临界坡陡坡缓坡)()()(000k k k kk kh h i i h h i i h h i i §7-3 缓流、急流、临界流及其判别准则(明渠水流的三种流态)明渠水流在临界水深时的流速为临界流速,以v k 表示,这样的水流状态称之为临界流。
当流速小于临界流速时,称之为缓流。
大于临界流速时,称之为急流。
急流、缓流的判别通常采用临界水深判别法和弗汝德数判别法。
一、临界流速(或临界水深)判别法k k v h →—临界流速 (1)缓流:v <v k ,h >h k ,0>dhde,e 为增函数,比能曲线上支。
(2)急流:v >v k ,h <h k ,0<dhde,e 为减函数,比能曲线下支。
(3)临界流:v =v k ,h =h k ,0=dhde,极值点。
二、弗汝德数判别法(1)定义:32ωαg BQ F r =-----无量纲数 r F B g Q dh de -=-=1132ωα (2)r F 的物理意义hg v h g v h g Q g B Q F r 221222232ααωαωα==== (其中B ω=) F r 表示过水断面单位重量液体的平均动能与平均势能比值的二倍。
(3)判别:101==-=r r F F dh de缓流临界流急流111<=>r r r F F F流态判别参考下表:思考题:一宽矩形渠道,底坡为i ,流量为Q ,作均匀流动,试问:(1)如原来为缓流,当流量增加或减小时,能否变为急流?(仍作均匀流) (2)如原来为急流,当流量增加或减小时,能否变为缓流?32gq h K α=)()(151032qf qf h K ==i h nq 3501=)()(159530q f q f h == 随q 增加,K h 比0h 增加快§7-4 水跃 一、水跃现象明渠水流从急流到缓流时水面骤然跃起的局部水力现象叫水跃。
在水跃发生的流段内,流速分布及其大小不断变化,水跃区域的上部为饱掺空气的表面漩滚似的水涡,称为旋滚区,下部为在铅直平面内急剧扩张前进的水流,称为主流区。
条件:从急流过渡到缓流 二、水跃的基本方程仅讨论平坡渠道中的完整水跃(发生在棱柱形渠道、其跃前水深'h 和跃后水深"h 相差显著的水跃,因水头损失未知,应用动量方程)。
假设:1 水跃段长度不大,渠床的摩擦阻力较小,可忽略。
即0≈f F 。
2 跃前、后断面的水流为渐变流、符合静压分布。
3 取121==ββ对1-1、2-2断面间的水体建立动量方程f F P P v v gQ--=-2112)(γ,11ωQv =,22ωQv =其中:222111ωωy P y P ==;1y 表示跃前断面形心点到液面的距离,2y 表示跃后断面形心点到液面的距离。
为共轭水深水跃函数令完整水跃的基本方程"'"'222221112)()()(h h h h y g Q h y g Q y g Q θθωωθωωωω=---+=---+=+∴三、水跃函数的图形水跃函数时水深的连续函数,可以用图形表示。
水跃函数的图形见右图。
∞→→→)(00h h θω时∞→∞→∞→)(h h θω时特性:1、)(h θ最小值对应的水深为临界水深K h 。
2、当K h h >时,)(h θ随h 的增加而增加,K h h <时,)(h θ随h 的增加而减小。
3、上支为缓流,下支为急流。
4、一个水跃函数值对应两个h ,二者为共轭水深。
5、跃前水深越大,对应的跃后水深越小,反之亦然。
四、共轭水深的计算1、一般方法:绘制水跃函数曲线的上支或下支2、矩形渠道0.1232======αβαωk h gq bQ q h y bh)2()2(2)(2322222h h h b h gh q b bh h gbh q b y g Q h k +=+=+=+=ωωθ因为 )()("'h h θθ=所以 )2()2(2""32''3h hh b h h h b K K +=+ 3"'"'2)(K h h h h h =+ 或 0232"'"2'=-+K h h h h h]1)(81[23""'-+=h h h h K ]1)(81[23''"-+=hh h h K2322"223"23")(r K F g bQ gh v gh q h h ====ω其中: 13'23')(r K F ghq h h == 所以 ]181[23"2"'-+=gh q h h ]181[22"-+=r F h]181[23'2'"-+=gh q h h ]181[21'-+=r F h五、水跃的能量损失与长度1、能量损失由水跃造成的绝大部分的能量损失 集中于水跃区域,极小部分能量损失发生于跃后流段,因此通常认为完全发生在水跃段。
对于平底情况"'222"211'2222221111)2()2()2()2(e e gv h gv h gv p z gv p z h -=+-+=++-++=∆αααγαγω将323"'"'2)(gq h h h h h h K Kα==+与代入上式h h h h h h h h h h h h h h h h h h h h h h h h h h h h h h h h k k k w '''''+''-''+''-'=''''-''''+''''+''-'=''''-''+''-'=''-'+''-'=∆4))(()()(4)()()(2)()22()(222222222232323 "'3"4)'(hh h h h w -=∆ 2、水跃长度 0l l l y +==水跃段+跃后段 §7-5 明渠恒定非均匀渐变流的基本微分方程以0-0为基准面建立1-1、2-2断面的能量方程wdh gdv v dh h dz z gv h z ++++++=++2)()()(220020αα)2(2])(2[22)(22222gv d gv dv vdv v ggdv v αααα+≈++=+因为f dh gv d gv dh h dz z gv h z ++++++=++∴)2(22220020ααα因为 ids dz -=0ds RC Q ds K Q dh dh gv d dh ids f f222222)2(ωα=≈++=所以所以ds dsKQ g v d dh ids 同除以222)2(++=∴αds d g Q ds dh g Q ds d ds dh g v ds d ds dh KQ i ωωαωαα3222222)2()2(-=+=+=- ),(s h f =ωs ds dh B s ds dh h ds d ∂∂+=∂∂+∂∂=ωωωω (对某一断面:B h=∂∂ω) 对于棱柱形渠道 0=∂∂sωdsdh g B Q K Q i )1(3222ωα-=- r F K Q i Bg Q K Q i ds dh --=--=11223222ωα §7-6 棱柱形渠道恒定非均匀渐变流水面曲线的分析 一、水面曲线的类型1、底坡的划分(1)明渠按底坡可分为三种情况:顺坡(i>0),平坡(i=0),逆坡(i<0)。
(2)对于正坡渠道,根据临界坡又分为三种情况:缓坡(i<i k ),陡坡(i>i k ),临界坡(i=i k )。
2、流区的划分(1)在正坡渠道中,存在均匀流水面线,称为正常水深线(N-N 线);存在临界水深线(K-K 线)。
(2)在平坡、逆坡渠道中,不存在N-N 线,只存在K-K 线。
(3)以N-N 、K-K 线为标志将水流分区。
在N-N 、K-K 线以上的区叫a 区,介于二者之间的区叫b 区,在两线之下的区叫c 区。