传动轴的强度及刚度计算
- 格式:ppt
- 大小:899.00 KB
- 文档页数:32




轴的强度校核方法摘要轴是机械中非常重要的零件,用来支承回转运动零件,如带轮、齿轮、蜗轮等,同时实现同一轴上不同零件间的回转运动和动力的传递。
轴的设计时应考虑多方面因素和要求,其中主要问题是轴的选材、结构、强度和刚度。
其中对于轴的强度校核尤为重要,通过校核来确定轴的设计是否能达到使用要求,最终实现产品的完整设计。
本文根据轴的受载及应力情况采取相应的计算方法,对于1、仅受扭矩的轴2、仅受弯矩的轴3、既承受弯矩又承受扭矩的轴三种受载情况的轴的强度校核进行了具体分析,并对如何精确计算轴的安全系数做了具体的简绍。
校核结果如不满足承载要求时,则必须修改原结构设计结果,再重新校核。
轴的强度校核方法可分为四种:1)按扭矩估算2)按弯矩估算3)按弯扭合成力矩近视计算4)精确计算(安全系数校核)关键词:安全系数;弯矩;扭矩目录第一章引言--------------------------------------- 11.1轴的特点---------------------------------------------1 1.2轴的种类---------------------------------------------1 1.3轴的设计重点-----------------------------------------1第二章轴的强度校核方法----------------------------42.1强度校核的定义-------------------------------------42.2轴的强度校核计算-----------------------------------42.3几种常用的计算方-----------------------------------52.3.1按扭转强度条件计算-------------------------------52.3.2按弯曲强度条件计算-------------------------------62.3.3按弯扭合成强度条件计算---------------------------72.3.4精确计算(安全系数校核计算)----------------------92.4 提高轴的疲劳强度和刚度的措施---------------------12 第三章总结------------------------------------------13参考文献--------------------------------------------14第一章引言1.1轴的特点:轴是组成机械的主要零件之一。


基础篇之四第4章 圆轴扭转时的强度与刚度计算杆的两端承受大小相等、方向相反、作用平面垂直于杆件轴线的两个力偶,杆的任意两横截面将绕轴线相对转动,这种受力与变形形式称为扭转(torsion )。
本章主要分析圆轴扭转时横截面上的剪应力以及两相邻横截面的相对扭转角,同时介绍圆轴扭转时的强度与刚度设计方法。
4-1 外加扭力矩、扭矩与扭矩图作用于构件的外扭矩与机器的转速、功率有关。
在传动轴计算中,通常给出传动功率P 和转递n ,则传动轴所受的外加扭力矩M e 可用下式计算:[][]e kw 9549[N m]r /min P M n =⋅其中P 为功率,单位为千瓦(kW );n 为轴的转速,单位为转/分(r/min )。
如功率P 单位用马力(1马力=735.5 N •m/s ),则e []7024[N m][r /min]P M n =⋅马力 外加扭力矩M e 确定后,应用截面法可以确定横截面上的内力—扭矩,圆轴两端受外加扭力矩M e 作用时,横截面上将产生分布剪应力,这些剪应力将组成对横截面中心的合力矩,称为扭矩(twist moment ),用M x 表示。
图4-1 受扭转的圆轴用假想截面m -m 将圆轴截成Ⅰ、Ⅱ两部分,考虑其中任意部分的平衡,有M x -M e = 0由此得到图4-3 剪应力互等M x = M e与轴力正负号约定相似,圆轴上同一处两侧横截面上的扭矩必须具有相同的正负号。
因此约定为:按右手定则确定扭矩矢量,如果横截面上的扭矩矢量方向与截面的外法线方向一致,则扭矩为正;相反为负。
据此,图4-1b 和c 中的同一横截面上的扭矩均为正。
当圆轴上作用有多个外加集中力矩或分布力矩时,进行强度计算时需要知道何处扭矩最大,因而有必要用图形描述横截面上扭矩沿轴线的变化,这种图形称为扭矩图。
绘制扭矩图的方法与过程与轴力图类似,故不赘述。
【例题4-1】 变截面传动轴承受外加扭力矩作用,如图4-2a 所示。
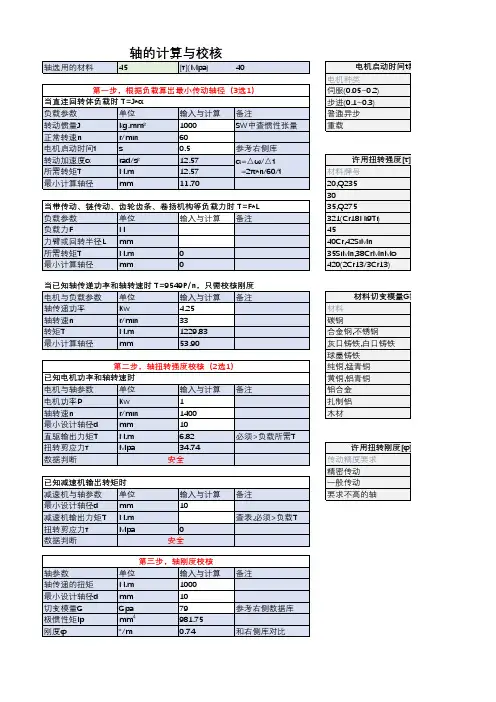



任务十三传动轴的扭转强度计算与变形验算传动轴是一种常见的机械传动元件,其主要功能是将发动机的功率传递给车轮,从而驱动汽车行驶。
在传动轴的工作过程中,由于扭矩的作用,会产生轴的扭转变形和扭转应力,因此需要对传动轴的扭转强度和变形进行计算和验算。
首先,我们需要计算传动轴的扭转强度。
传动轴的扭转强度是指传动轴能够承受的最大扭矩,并且不会发生破坏的能力。
其计算公式为:τ max = T_max / (π/16) * (d^3 / J)其中,τ max 为传动轴的最大扭矩应力,T_max 为传动轴所承受的最大扭矩,d为传动轴的直径,J为传动轴截面的极性矩。
接下来,我们需要计算传动轴的变形。
传动轴的变形通常是以弯曲变形为主,而对于小直径的传动轴来说,扭转变形可以忽略不计。
传动轴的弯曲变形可以通过弹性力学理论来计算,其计算公式为:δ=(M*L)/(E*I)其中,δ为传动轴的弯曲变形,M为传动轴上的弯矩,L为传动轴的长度,E为传动轴的杨氏模量,I为传动轴的截面惯性矩。
在进行传动轴的变形验算时,需要将传动轴的实际变形与允许变形进行比较。
一般来说,传动轴的允许变形不能超过其长度的百分之一,即δ≤L/100。
如果计算得到的传动轴的实际变形小于或等于允许变形,则传动轴符合扭转强度和变形的要求,可以继续使用;如果计算得到的传动轴的实际变形大于允许变形,则需要对传动轴进行改进或重新设计。
在进行传动轴的扭转强度计算和变形验算时,还需考虑材料的强度。
传动轴通常采用高强度材料,如合金钢、不锈钢等。
根据材料的强度参数,可以计算得到传动轴的极限弯矩和极限扭矩。
在实际运行中,传动轴的工作状态应远远低于其极限弯矩和极限扭矩,以确保其可靠性和安全性。
综上所述,传动轴的扭转强度计算和变形验算是传动轴设计和制造中的重要环节。
通过合理计算和验算,可以确保传动轴具备足够的强度和刚度,从而达到良好的传动性能和工作可靠性。
在实际应用中,还需考虑传动轴的其他因素,如动平衡、润滑等,以进一步提高传动轴的工作效能。

轴的设计计算轴的计算通常都是在初步完成结构设计后进行校核计算,计算准则是满足轴的强度和刚度要求。
一、轴的强度计算进行轴的强度校核计算时,应根据轴的具体受载及应力情况,采取相应的计算方法,并恰当地选取其许用应力。
对于仅仅承受扭矩的轴(传动轴),应按扭转强度条件计算;对于只承受弯矩的轴(心轴),应按弯曲强度条件计算;对于既承受弯矩又承受扭矩的轴(转轴),应按弯扭合成强度条件进行计算,需要时还应按疲劳强度条件进行精确校核。
此外,对于瞬时过载很大或应力循环不对称性较为严重的轴,还应按峰尖载荷校核其静强度,以免产生过量的塑性变形。
下面介绍几种常用的计算方法:按扭转强度条件计算。
1、按扭转强度估算轴的直径对只受转矩或以承受转矩为主的传动轴,应按扭转强度条件计算轴的直径。
若有弯矩作用,可用降低许用应力的方法来考虑其影响。
扭转强度约束条件为:[]式中:为轴危险截面的最大扭剪应力(MPa);为轴所传递的转矩(N.mm);为轴危险截面的抗扭截面模量();P为轴所传递的功率(kW);n为轴的转速(r/min);[]为轴的许用扭剪应力(MPa);对实心圆轴,,以此代入上式,可得扭转强度条件的设计式:式中:C为由轴的材料和受载情况决定的系数。
当弯矩相对转矩很小时,C值取较小值,[]取较大值;反之,C取较大值,[]取较小值。
应用上式求出的值,一般作为轴受转矩作用段最细处的直径,一般是轴端直径。
若计算的轴段有键槽,则会削弱轴的强度,作为补偿,此时应将计算所得的直径适当增大,若该轴段同一剖面上有一个键槽,则将d增大5%,若有两个键槽,则增大10%。
此外,也可采用经验公式来估算轴的直径。
如在一般减速器中,高速输入轴的直径可按与之相联的电机轴的直径估算:;各级低速轴的轴径可按同级齿轮中心距估算,。
几种轴的材料的[]和C值[]2、按弯扭合成强度条件校核计算对于同时承受弯矩和转矩的轴,可根据转矩和弯矩的合成强度进行计算。
计算时,先根据结构设计所确定的轴的几何结构和轴上零件的位置,画出轴的受力简图,然后,绘制弯矩图、转矩图,按第三强度理论条件建立轴的弯扭合成强度约束条件:考虑到弯矩所产生的弯曲应力和转矩所产生的扭剪应力的性质不同,对上式中的转矩乘以折合系数,则强度约束条件一般公式为:式中:称为当量弯矩;为根据转矩性质而定的折合系数。