控制系统设计的根轨迹法
- 格式:ppt
- 大小:215.50 KB
- 文档页数:17




第4章 根 轨 迹 法根轨迹法是分析和设计线性控制系统的图解方法,使用简便,在控制工程上得到了广泛应用。
本章首先介绍根轨迹的基本概念,然后重点介绍根轨迹绘制的基本法则,在此基础上,进一步讨论广义根轨迹的问题,最后介绍控制系统的根轨迹分析方法。
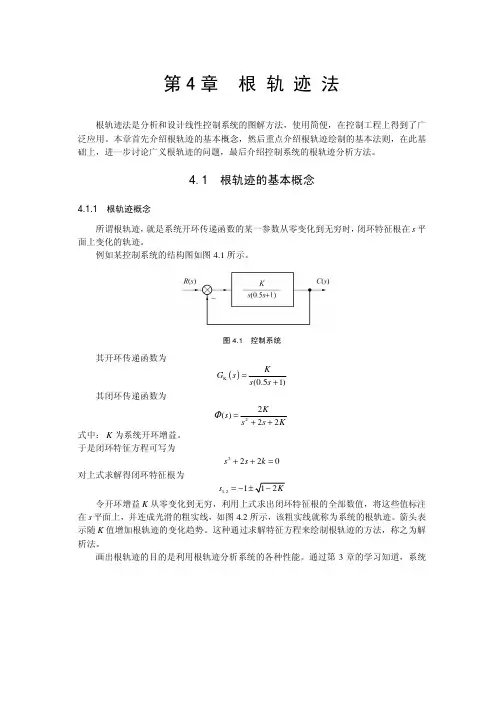
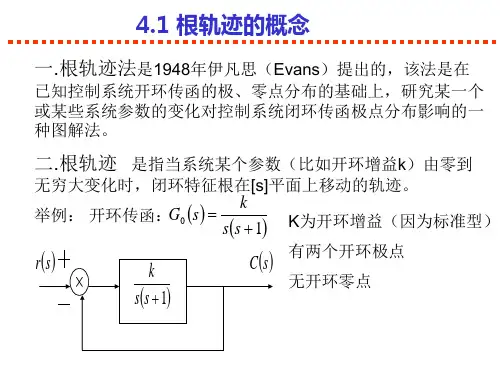
4.1 根轨迹的基本概念4.1.1 根轨迹概念所谓根轨迹,就是系统开环传递函数的某一参数从零变化到无穷时,闭环特征根在s 平面上变化的轨迹。
例如某控制系统的结构图如图4.1所示。
图4.1 控制系统其开环传递函数为()K (0.51)KG s s s =+其闭环传递函数为22()22Ks s s KΦ=++式中:K 为系统开环增益。
于是闭环特征方程可写为2220s s k ++=对上式求解得闭环特征根为1,21s =−令开环增益K 从零变化到无穷,利用上式求出闭环特征根的全部数值,将这些值标注在s 平面上,并连成光滑的粗实线,如图4.2所示,该粗实线就称为系统的根轨迹。
箭头表示随K 值增加根轨迹的变化趋势。
这种通过求解特征方程来绘制根轨迹的方法,称之为解析法。
画出根轨迹的目的是利用根轨迹分析系统的各种性能。
通过第3章的学习知道,系统第4章 根轨迹法·101··101·特征根的分布与系统的稳定性、暂态性能密切相关,而根轨迹正是直观反应了特征根在复平面的位置以及变化情况,所以利用根轨迹很容易了解系统的稳定性和暂态性能。
又因为根轨迹上的任何一点都有与之对应的开环增益值,而开环增益与稳态误差成反比,因而通过根轨迹也可以确定出系统的稳态精度。
可以看出,根轨迹与系统性能之间有着比较密切的联系。
图4.2 控制系统根轨迹4.1.2 根轨迹方程对于高阶系统,求解特征方程是很困难的,因此采用解析法绘制根轨迹只适用于较简单的低阶系统。
而高阶系统根轨迹的绘制是根据已知的开环零、极点位置,采用图解的方法来实现的。
下面给出图解法绘制根轨迹的根轨迹方程。



控制系统根轨迹法控制系统的设计和分析是现代工程领域中的重要任务。
为了实现系统的稳定性和性能要求,控制系统工程师采用了多种方法和技术。
其中,根轨迹法是一种常用且有效的方法,用于评估和改进系统的动态响应。
1. 系统根轨迹方法概述控制系统根轨迹方法是基于系统的传递函数,通过分析系统在复平面上的极点和零点位置来评估系统的稳定性和动态性能。
在根轨迹图中,系统的极点和零点以及传递函数的增益可以直观地展示出来,从而帮助工程师定量地了解系统的响应特性。
2. 根轨迹图的构造根轨迹图通常由两个主要的部分组成:实部为-1的轴线和虚部为0的轴线。
系统的传递函数通常表示为连续时间的形式,并且可以表示为一个或多个一阶和二阶传递函数的乘积。
根轨迹图的构造基于这些传递函数的极点和零点。
极点和零点对应于根轨迹图上的曲线,其中极点表示系统的稳定性,而零点则表示系统的过渡性能。
3. 根轨迹与稳定性根轨迹图提供了系统稳定性的重要信息。
通过观察根轨迹图,可以确定系统的稳定性。
如果根轨迹图上的所有的极点都位于左半平面,那么系统是稳定的。
相反,如果存在极点位于右半平面,系统是不稳定的。
通过调整参数或者设计控制器,可以将系统的极点移动到左半平面,从而提高系统的稳定性。
4. 根轨迹与动态响应除了稳定性,根轨迹图还提供了关于系统动态响应的信息。
通过观察根轨迹图上的曲线形状,可以了解系统的过渡特性。
例如,当根轨迹密集且靠近虚部为0的轴线时,说明系统的过渡响应非常快。
相反,当根轨迹离散且远离虚部为0的轴线时,说明系统的过渡响应比较慢。
通过分析根轨迹图,工程师可以调整系统参数来改善系统的动态响应性能。
5. 根轨迹的应用根轨迹方法是控制系统分析和设计中常用的工具之一。
它可以用于多个方面,包括控制器的设计、系统的稳定性分析和性能优化。
使用根轨迹方法,工程师可以确定合适的控制器增益、相位补偿器和频率补偿器来满足系统的设计要求。
6. 根轨迹法的局限性尽管根轨迹法在控制系统领域中被广泛应用,但它也有一些局限性。