当前位置：文档之家 › 自动控制原理 题库 第四章 线性系统根轨迹 习题

自动控制原理 题库 第四章 线性系统根轨迹 习题

  • 格式：doc
  • 大小：1.16 MB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

夏德钤《自动控制原理》（第4版）章节题库-第4章线性系统的根轨迹分析【圣才出品】

夏德钤《自动控制原理》（第4版）章节题库-第4章线性系统的根轨迹分析【圣才出品】

夏德钤《⾃动控制原理》（第4版）章节题库-第4章线性系统的根轨迹分析【圣才出品】第4章　线性系统的根轨迹分析1．系统的开环传递函数试证明：点在根轨迹上，并求出相应的和系统开环增益K。

证明：根据系统的开环传递函数可知，系统的开环极点为由闭环根轨迹的相⾓条件可得：当时，故点在根轨迹上。

由闭环根轨迹的幅值条件可知，此时即相应的根轨迹增益和系统开环增益仿真曲线如图4-1所⽰。

MATLAB程序：exe402.m２．设单位反馈控制系统的开环传递函数为试⽤解析法绘出K*从零变到⽆穷时的闭环根轨迹图，并判断下列点是否在根轨迹上：（﹣2＋j0），（0＋j1），（﹣3＋j2）解：闭环传递函数为则闭环特征⽅程为闭环特征根为当。

可逐个描点得闭环根轨迹如图4-2所⽰，从图4-2中明显可见，只有（－2，j0）在根轨迹上。

图4-2３．设单位反馈控制系统的开环传递函数如下，试概略绘制闭环根轨迹图。

解：（1）系统的开环传递函数令为根轨迹增益。

①实轴上的根轨迹：[0，－2]，[－5，－∞）。

②根轨迹的渐近线：③根轨迹的分离点：根轨迹的分离点坐标满⾜解得④根轨迹与虚轴的交点：由系统的开环传递函数可知系统的闭环特征⽅程令s＝jω，将其代⼊上式可得即由于ω≠0，故可解得则根轨迹与虚轴的交点为±j3.16。

根据以上⼏点，可以画出概略根轨迹如图4-3所⽰。

图4-3 系统（1）概略根轨迹图（2）系统的开环传递函数①实轴上的根轨迹[0，－2]，[－3，－5]。

③根轨迹的分离点：根轨迹的分离点坐标满⾜通过试凑可得d＝－0.89。

根据以上⼏点，可以画出概略根轨迹如图4-4所⽰。

图4-4 系统（2）概略根轨迹图（3）系统的开环传递函数①实轴上的根轨迹：[－1，－3]，[－10，－5]。

②根轨迹的渐近线：③根轨迹的分离点：根轨迹的分离点坐标满⾜通过试凑可得d＝－7.27。

根据以上⼏点，可以画出概略根轨迹如图4-5所⽰。

图4-5 系统（3）概略根轨迹图（4）系统的开环传递函数实轴上的根轨迹为[－2，－1]，系统概略根轨迹如图4-6所⽰。

自动控制原理第第四章 线性系统的根轨迹法

自动控制原理第第四章 线性系统的根轨迹法

2
自动控制原理
§4.1 根轨迹的基本概念
例：开环传递函数
Gs
k1
ss
a
开环系统两个极点为：P1 0, P2 a R(s)
闭环传递函数为:
GB s
s2
k1 as
k1
-
k1
C(s)
ss a
闭环特征方程： s2 as k1 0
闭环特征根：s1,2
a 2
a 2
2
k1
（闭环极点）
3
自动控制原理
在p5附近取一实验点sd， 则∠sd-p5可以认为是p5点的出射角 Sd Z Sd P1 Sd P2 Sd P3 Sd P4 Sd P5 1800
近似为 P5 Z P5 P1 P5 P2 P5 P3 P5 P4 p 1800
p Sd P5 1800
法则4 实轴上存在根轨迹的条件——
这些段右边开环零极点个数之和为奇
数。
m
n
证明：根据相角条件 S Z j S Pi 18002q 1
j 1
i 1
p4
j s平面
例：sd为实验点
p3
z2 sd
p2 z1 p1
p5
① 实验点sd右侧实 轴上零极点提供 1800相角
③ 共轭复零点，复极点提供的相角和为 3600。
2
s1=-1.172，s2＝-6.828
33
自动控制原理
法则6 开环复数极点处根轨迹出射角为
p 1800
开环复数零点处根轨迹入射角为：
Z 1800
其中 z p（不包括本点）
34
自动控制原理
j p5
p5
p3 p3
p2

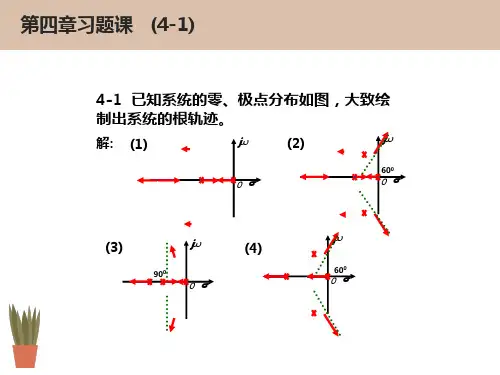
自动控制原理课后习题第四章答案

自动控制原理课后习题第四章答案

G(s)H(s)=
Kr s(s+1)(s+3)
σ根 s=3-K+ω轨r4-3-迹+p4s132ω1-3的+~3ω32分p===s2-离+001K点.p-3r=3：KK~0θrr===012+ωω6021,o=3,=0+±1810.7o
8
jω
1.7
s1
A(s)B'系(s)统=根A'轨(s迹)B(s)
s3 p3
s=sK2±r没=j24有.8.6位×于2K.r根6=×4轨80.迹6=上7，. 舍去。
2
第四章习题课 (4-9)
4-9 已知系统的开环传递函数，(1) 试绘制出
根轨迹图。
G(s)H与(s虚)=轴s交(0点.01s+1K)(系0.统02根s+轨1迹)
jω
70.7
解: GKK(rr=s=)10H5(0s)=ωω2s1,(3=s=0+±17000K.7)r(s+50)
s1
A(s)B'(系s)统=A根'(轨s)迹B(s)
s3 p3
p2
p1
-4
-2
0
((24))ζ阻=尼03.振5s2荡+1响2应s+s的81==K-r0值0.7范+围j1.2
s=s-s10=3=.-80-56.8+50K.7r×=20=s.82-=54×-.631..1155×3.15=3.1
-2.8
450
1080
360
0σ
0σ
第四章习题课 (4-2)
4-2 已知开环传递函数，试用解析法绘制出系
统的根轨迹，并判断点(-2+j0),(0+j1),

自动控制原理 第四章习题集配套答案

自动控制原理 第四章习题集配套答案

第四章 根轨迹分析法习题4-2 单位回馈控制系统的开环传递函数1)(+=s K s G r，试用解析法绘出r K 从零变化到无穷时的死循环根轨迹图，并判断-2, j1, (-3+j2)是否在根轨迹上。

解：1-s 01s 0r=⇒=+=时，K2-s 02s 1r=⇒=+=时，K3-s 03s 2r=⇒=+=时，K……-2 在根轨迹上，（-3+j2），j1不在根轨迹上。

4-3 回馈控制系统的开环传递函数如下，0≥r K ，试画出各系统的根轨迹图。

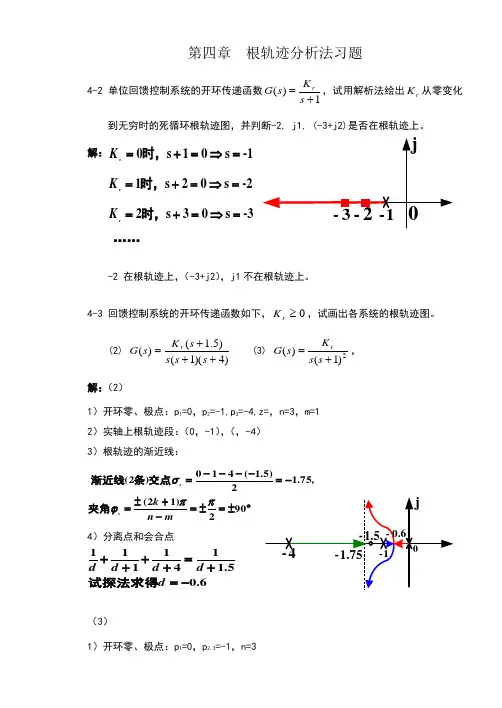
(2) )4)(1()5.1()(+++=s s s s K s G r (3) 2)1()(+=s s K s G r ， 解：（2）1）开环零、极点：p 1=0，p 2=-1,p 3=-4,z=，n=3，m=1 2）实轴上根轨迹段：（0，-1），（，-4） 3）根轨迹的渐近线：︒±=±=-+±=-=----=902)12(,75.12)5.1(410)2( ππϕσm n k aa夹角交点条渐近线4）分离点和会合点6.05.1141111-=+=++++d d d d d 试探法求得（3）2）实轴上根轨迹段：（0，-1），（-1，-∞） 3）根轨迹的渐近线：±=-+±=-=--=3)12(,323110)3( ππϕσm n k aa夹角交点条渐近线4）分离点和会合点310121-=⇒=++d d d 5）与虚轴交点：223++s s4-5 系统的开环传递函数为)1()2()(++=s s s K s G r ，(1) 画出系统的根轨迹，标出分离点和会合点；(2) 当增益r K 为何值时，复数特征根的实部为-2求出此根。

解： （1）1）开环零、极点：p 1=0，p 22）实轴上根轨迹段：（0，-13）分离点和会合点.3,586.02111121-=-=⇒+=++d d d d d123ss s s r2K-r211K rKj,202rr±==⇒=-s K K（2）系统特征方程为02)1(rr2=+++K s K s2j 2322122,1rr±-==-=+-=-s K Ka b ，，得：由4-6 单位回馈系统的前向信道函数为)3)(1()(++=s s s K s G r，为使死循环主导极点具有阻尼比5.0=ξ，试确定r K 的值。

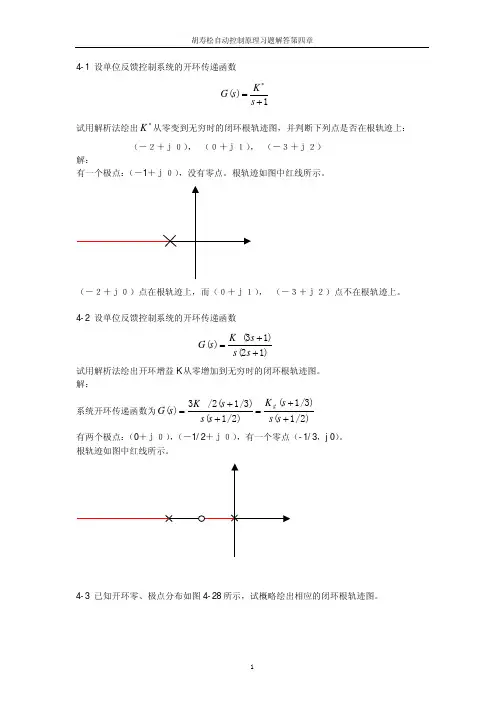
自动控制原理第四章习题解答

自动控制原理第四章习题解答
根轨迹如图中红线所示。
4
胡寿松自动控制原理习题解答第四章
（２） G(s) =
K ∗ (s + 20)
。
s(s + 10 + j10)(s + 10 − j10)
解：
系统开环传递函数为 G(s) =
K ∗ (s + 20)
s(s + 10 + j10)(s + 10 − j10)
有三个极点：p1 =（0，j0），p2 =（-10＋ｊ10），p3 =（－10-ｊ10），有一个零点 z1 =（－
(2) 确定 G(s) = K ∗ (s + z)
产生纯虚根为±ｊ1 的ｚ值和 K ∗ 值。
s 2 (s + 10)(s + 20)
解：系统特征方程为 s4 + 30s3 + 200s2 + K *s + K *z = 0 令 s = j1代入特征方程中得：
20，ｊ０）。 起始角：
∑ ∑ θ pi
= (2k
+ 1)π
+
m
ϕ z j pi
j =1
n
−
θ pi pi
j =1
( j≠i)
k = 0,±1,±2,L
θ p1 = 1800
θ p2 = 1800 ϕ + z1p2 θ − p1p2 θ − p3p2 = 1800 + 450 − 1350 − 900 = 00
有两个极点：（0＋ｊ０），（－0.5＋ｊ０），有一个零点（－1＋ｊ０）。
分离点坐标计算如下：
1+ 1 = 1 d d + 0.5 d + 1
d 2 + 2d + 0.5 = 0 解方程的 d1 = −1.7 ， d2 = −0.29

自动控制原理-第四章 线性系统的根轨迹法(4)

自动控制原理-第四章 线性系统的根轨迹法(4)

暂态响应呈振荡性质，其超调量主要取决于主导极点的衰
减率
1 n

d n 1 2
1 2
并与其它极点接近原点的程度有关，调整时间主要取决于主
导极点的实部
1


。
n
（4）调节时间。调节时间主要取决于最靠近虚轴的闭环复数
极点的实部绝对值 1 n 。
（5）实数零、极点影响。闭环极点的存在会增大系统的阻尼比， 使响应速度减慢，超调量减少。闭环零点的存在减小系统阻尼， 使响应速度加快，超调量增加。
4-4 系统性能的分析
系统闭环零、极点位置与暂态响应的关系：
（1）稳定性。系统的稳定性只取决于闭环极点的位置。
（2）运行形式。如果闭环系统无零点，闭环极点均为实数 极点，则系统的暂态响应为单调的；如果闭环极点均为复 数极点，则系统的暂态响应为振荡的。
（3）超调量。如果系统具有一对闭环主导极点，则系统的
4-7 线性系统根轨迹分析的MATLAB方法
1、绘制零极点分布图 ：[ p,z]=pzmap(sys);
2、绘制根轨迹图 绘制根轨迹一般步骤为： (1)先将特征方程写成 1 A P(s) 0 形式，得到等效的开 环传递函数 G A P(s) ； Q(s)
Q(s)
(2)调用rlocus命令绘制根轨迹。
Hale Waihona Puke （6）偶极子及其影响。如果系统中存在非常接近的零点和极 点，其相互距离比其本身的模值小一个数量级以上，则把这对 闭环零、极点称为偶极子。偶极子的位置距离原点非常近时， 其对暂态响应的影响一般需要考虑，但不会影响闭环主导极点 的主导作用。偶极子的位置距离原点较远时，其对暂态响应的 影响可以忽略。 （7）主导极点及高阶系统化简。在s平面上，离虚轴靠 近而附近又没有其它闭环零点的一些闭环极点 ，对系统 影响最大，称为主导极点。凡比主导极点的实部大3～6 倍以上的其他闭环零、极点，其影响均可忽略不计。对 于高阶系统，略去不十分靠近原点的偶极子，保留一个 或几个最靠近虚轴又不十分靠近闭环零点的主导极点， 将高阶系统简化为只有一、两个闭环零点和两、三个闭 环极点的二阶或三阶系统。

自动控制原理第4章习题解——邵世凡

自动控制原理第4章习题解——邵世凡

第四章 习题4-1 绘制具有下列开环传递函数的负反馈系统的根轨迹1、()()()()54*++=s s s K s H s G解：首先确定开环传递函数中的零极点的个数各是多少。

由开环传递函数可知 m=0，n=3，n -m=3。

即，有限零点为0个，开环极点为3个。

其中，3个开环极点的坐标分别为：p 1=0，p 2=-4，p 3=-5。

然后，在[s]平面上画出开环极点的分布情况，根据根轨迹方程的幅角条件：首先确定实轴上的闭环系统的根轨迹。

如图所示。

接着再通过所需参数的计算画出比较精确的根轨迹通过画实轴上的根轨迹图可知，有3条闭环根轨迹，分别从p 1=0，p 2=-4，p 3=-5出发奔向无穷远处的零点。

在这一过程中，从p 1=0，p 2=-4两个极点出发的根轨迹在实轴上相遇后进入复平面，因此，有必要进行分离点的坐标计算，渐进线在实轴上的坐标点和渐进线的角度计算，以及与虚轴交点的计算。

根据公式有：渐进线303054011-=----=--=∑∑==mn zp n i mj jiσ()() ,,331212ππππϕ±±=+=-+=k mn k a从p 1=0，p 2=-4两个极点出发的根轨迹在实轴上相遇后将沿着±60º进入复平面，分离点：设：()1=s N ；()()()s s s s s s s D 2095423++=++=；()0'=s N ；()201832'++=s s s D则有：()()()()()0201832''=++-=⋅-⋅s s s D s N s D s N[s ]0201832=++s s解得方程的根为s 1= -4.5275（不合题意舍去）；s 2= -1.4725 得分离点坐标：d = -1.4725。

与虚轴的交点：在交点处，s=j ω，同时也是闭环系统的特征根，必然符合闭环特征方程，于是有：()020********=++--=+++*=*K j j K s s sj s ωωωω整理得： 0203=-ωω；092=-*ωK 解得01=ω；203,2±=ω；18092==*ωK 最后，根据以上数据精确地画出根轨迹。

自动控制原理简明教程 第四章 根轨迹法 习题答案

自动控制原理简明教程 第四章 根轨迹法 习题答案

方程求得。
k* 2 3 3
2
1
2 3 2 2 3 1
解得： k* 3(3 3)
1 3
特征根s=0处对应的 k * 值也利用模值方程求得：
k* 3 2 2 1
1
k*
4 3
满足稳定性时，k* 4 要使系统的三个根均为负
实根，则：
3
k* 4 3
0 k* 3(3 3) 1 3
0 k*
另一个闭环极点为 S3 ，则
(S S3 )(S 1)2 S (S 3)2 4
则解得：
(S S3 )(S 1)2 S (S 1)2 4(S 1)2 (S 4)(S 1)2
则 (S S3) S 4 S3 4 （另外一个闭环极点） 临界阻尼时的闭环传递函数为
(S)
(S
4(S 1) 4)(S 1)2
(2
j) (2 3
j)
4 3
渐近线与实轴正方向夹角
a
(2k 1)
nm
,
3
分离点： 1 1 1 0
d d 2 j d 2 j
整理得：3d 2 8d 5 0
解得：d1,2
8 6
2
d1 1 d2 1.67
分离角
l
180 l
180 2
900
把 S j 代入特征方程：
1
k*
n
m
a
i 1
Pi Zi
i 1
nm
(3) (3) 3
2
渐近线与实轴正方向夹角：
a
(2k 1)
nm
, ,
33
分离点： 1 1 1 0
d d 3 d 3
解得：d 1, a S (S 3)2 (1) 4 4

第四章线性系统的根轨迹法

第四章线性系统的根轨迹法
2. 零度根轨迹： 1 实轴上根轨迹区间右侧开环零极点数目之和为偶数 2 实轴与渐近线正方向夹角2kπ/n-m 3 求出射角和入射角时2kπ
4 分离角不变
1-G(S)H(S)=0 G(K)=1 例题：开环传递函数：
绘制系统的根轨迹。
解：①n=3.所以根轨迹有三条。 ②极点： ③渐近线： 5 分离点：
令 1． 闭环零极点由前向通道的零点和反馈通道的极点构成，对于单 位负反馈系统的闭环零点就是开环零点。 2． 闭环极点与开环极点，开环零极点及根轨迹都有关系。
4）.根轨迹方程：
幅值条件： 相角条件： ①满足相角条件的点肯定是根轨迹上的点，相角条件是确定根轨迹 的充要条件。 ②幅值条件是用来确定根轨迹上的点所对应的根轨迹增益。 5）.绘制更轨迹的法则： ①根轨迹的连续性：根轨迹是连续变化的直线或曲线。 ②根轨迹的对称性：根轨迹位于幅平面的实轴上或对称的实轴上。 ③根轨迹的条数;等于系统的阶次。即：闭环特征根最高次幂。 ④根轨迹的起点和终点：起源于n个开环极点，终止于m个开环零点。 以及n-m个无穷远零点。
闭环极点。
解 （1）系统的开环极点为，，是根轨迹各分支的起点。由于 系统没有有限开环零点，三条根轨迹分支均趋向于无穷远处。 （2）系统的根轨迹有条渐进线
渐进线的倾斜角为 取式中的K=0，1，2，得=π/3，π，5π/3。
渐进线与实轴的交点为
三条渐近线如图的虚线所示。 （3）实轴上的根轨迹位于原点与－1点之间以及－2点的左边，如图中 的粗实线所示。 （4）确定分离点：系统的特征方程式为 即
所以 即： ②分离点： 证明：
②除以①式
无零点 分离点重根 ③分离角：指根轨迹进入分离点的切线方向与离开分离点的切线方向之 间的夹角。当l条根轨迹进入并立即离开分离点时 8）根轨迹的出射角和入射角： 出射角：起始于开环极点的根轨迹在起点处，切线方向与正实轴的夹 角。 入射角：终止于开环零点的根轨迹在终点处切线方向与正实轴的夹角。

自动控制原理-胡寿松-第四章-线性系统的根轨迹法.详解

自动控制原理-胡寿松-第四章-线性系统的根轨迹法.详解

系统的信号流图见图4-28，从信号流图中看出，系统中含有一个积分环节， 因此为1型系统，因此系统对阶跃输入信号的稳态误差为0。
K m 变化时系统的根轨迹， 2）为了绘制电动机传递系数（含放大器附加增益） 可将有关参数代入传递函数中，并将系统的特征方程进行整理，等价根轨迹增 益方程为：
1 K* P( s ) ( s 6.93 j 6.93)( s 6.93 j 6.93) 1 K * Q( s ) s 2 ( s 13.86)
当所有根轨迹分支都在左半平面时，系统稳定。 2) 稳态性能：
回忆：稳态性能主要取决于系统的开环增益和积分环节个数。
由根轨迹图不仅可以方便的确定开环增益和积分环节个数，而且可以根据给定系统 的稳态误差要求, 确定闭环极点位置的容许范围。
3)动态性能： 回忆：动态性能形态主要取决于系统的——闭环极点。 从根轨迹图上，可以直观地看到特征根随着参数的变化情况，从而，可以方便地 确定动态性能随着参数的变化情况。
K * lim
s

j 1 i 1 m
n
s pi s zj
lim s
s
nm
, 0 ,
nm nm
（无穷零点）
（无穷极点）
(n m 1)
（续）
且均为实数开环零、极点。
（续）
（续）
小结论： 由两个极点（实数极点或者复数极点）和一个有限零点组成的开环系 统，只要有限零点没有位于两个实数极点之间，当 K * 从零变化到无穷时， 闭环根轨迹的复数部分，是以有限零点为圆心，以有限零点到重根点的距 离为半径的一个圆，或圆的一部分。这在数学上是可以严格证明的。
例如，在上列程序之后增加语句： [k,p]=rlocfind(num,den)

《自动控制原理》第4章_根轨迹分析法

《自动控制原理》第4章_根轨迹分析法
一般有两个解，从中
因此求分离点和会合点公式： 可以判断是分离点或
N(s)D '(s) N '(s)D(s) 0 会合点，只有满足条
Kg 0
件Kg≥0的是有用解。
例4-1.设系统结构如图， 试绘制其概略根轨迹。
R(s)
k(s 1) c(s)
s(s 2)(s 3)
解：画出 s 平面上的开环零点（-1），开环极点（0， -2，-3）。
逆时针为正。（- ， ）
m
n
pj (2k 1) ( z j pi ) pj pi
j 1
j 1
ji
m
n
zi (2k 1) ( z j zi ) p j zi
j 1
j 1
j i
k 0,1,
k 0, 1,
例3.设系统开环传递函数为： G(s) Kg(s 1.5)(s 2 j)(s 2 j) s(s 2.5)(s 0.5 j1.5)(s 0.5 j1.5)
K
s1
00
0.5 1
1 1 j1
s2
K
K 2.5
2
K 1
1 K 0
1 j1
2 1
2 1 j 3 1 j 3
1 j 1 j
j
2
1
0
K 0.5
1
2
一、根轨迹的一般概念
开环系统（传递函数）的某一个参数从零变化到 无穷大时，闭环系统特征方程根在 s 平面上的轨迹 称为根轨迹。
根轨迹法:图解法求根轨迹。 借助开环传递函数来求闭环系统根轨迹。
nm
独立的渐近线只有（n-m）条 u=0,1…,(n-m-1)
（2）渐近线与实轴的交点
分子除以分母

自动控制原理-题库-第四章-线性系统根轨迹-习题

自动控制原理-题库-第四章-线性系统根轨迹-习题

4-1将下述特征方程化为适合于用根轨迹法进行分析的形式，写出等价的系统开环传递函数。

（1）210s cs c +++=，以c 为可变参数。

（2）3(1)(1)0s A Ts +++=，分别以A 和T 为可变参数。

（3）1()01I D P k k s k G s ss τ⎡⎤+++=⎢⎥+⎣⎦，分别以P k 、I K 、T 和τ为可变参数。

4-2设单位反馈控制系统的开环传递函数为(31)()(21)K s G s s s +=+试用解析法绘出开环增益K 从0→+∞变化时的闭环根轨迹图。

4-2已知开环零极点分布如下图所示，试概略绘出相应的闭环根轨迹图。

4-3设单位反馈控制系统的开环传递函数如下，试概略绘出相应的闭环根轨迹图（要求确定分离点坐标）。

（1）()(0.21)(0.51)KG s s s s =++（2）(1)()(21)K s G s s s +=+（3）(5)()(2)(3)K s G s s s s +=++4-4已知单位反馈控制系统的开环传递函数如下，试概略绘出相应的闭环根轨迹图（要求算出起始角）。

（1）(2)()(12)(12)K s G s s s j s j +=+++-（2）(20)()(1010)(1010)K s G s s s j s j +=+++-4-5设单位反馈控制系统开环传递函数如为*2()()(10)(20)K s z G s s s s +=++试确定闭环产生纯虚根1j ±的z 值和*K 值。

4-6已知系统的开环传递函数为*22(2)()()(49)K s G s H s s s +=++试概略绘出闭环根轨迹图。

4-7设反馈控制系统中*2()(2)(5)KG s s s s =++（1）设()1H s =，概略绘出系统根轨迹图，判断闭环系统的稳定性（2）设()12H s s =+，试判断()H s 改变后的系统稳定性，研究由于()H s 改变所产生的影响。

王建辉《自动控制原理》(课后习题 根轨迹法)【圣才出品】

王建辉《自动控制原理》(课后习题 根轨迹法)【圣才出品】

第4章　根轨迹法4-1 根轨迹法适用于哪类系统的分析？答：根轨迹法适用于分析高阶系统。

4-2 为什么可以利用系统开环零点和开环极点绘制闭环系统的根轨迹？答：绘制根轨迹的依据是幅角条件，而系统的幅角关系为式中：；为开环有限零点－z i 到s 的矢量幅角；为开环极点－p j 到s 的矢量幅角。

由此可知，可以利用系统开环零点和开环极点来绘制闭环系统的根轨迹。

4-3 绘制根轨迹的依据是什么？答：绘制根轨迹的依据是幅角条件，即幅角的和总等于。

4-4 为什么说幅角条件是绘制根轨迹的充分必要条件？答：由根轨迹的定义可知，根轨迹由特征方程式的幅值条件和幅角条件决定，但因为K g 在0→∞范围内连续变化，总有一个K g 能满足幅值条件，所以，绘制根轨迹的依据是幅角条件。

4-5 系统开环零、极点对根轨迹形状有什么影响？答：（1）增加开环零点将使系统的根轨迹向左弯曲，并在趋向于附加零点的方向发生变形。

（2）增加开环极点将使系统的根轨迹向右弯曲，使对应同一个K g值的复数极点的实数部分和虚数部分数值减小，从而系统的调节时间加长，振荡频率减小。

4-6 求下列各开环传递函数所对应的负反馈系统的根轨迹。

解：（1）①起点：两个开环极点为－p1＝－1，－p2＝－2；终点：系统有一个开环有限零点为－z＝－3。

②实轴上的根轨迹区间为（－∞，－3]，[－2，－1]。

③根轨迹的分离点、会合点计算。

即因为根轨迹在（－∞，－3]和[－2，－1]上，所以，分离点为－1.58，会合点为－4.42。

根轨迹如图4-1所示。

图4-1 题4-6（1）根轨迹图（2）①起点：三个开环极点－p1＝0，－p2＝－3，－p3＝－2；终点：系统有一个开环有限零点－z＝－5。

②实轴上根轨迹区间为[－5，－3]，[－2，0]。

③渐近线倾角及交点计算。

由公式求得根轨迹的渐近线倾角和渐近线与实轴的交点为④求分离点N'（s）D（s）－D'（s）N（s）＝0。

自动控制原理-第四章-根轨迹

自动控制原理-第四章-根轨迹

snm 1 p1 1 pn

s
s
0
s z1 s zm
1 z1 1 zm
s
s
s pi i 1, 2, n
K*
s p1 s pn
snm 1 p1 1 pn

s
s

s z1 s zm
1 z1 1 zm

s(0.5s 1) s(s 2)
通过系统的根轨迹图，可以很方便地对系统的动态性能和稳态性能进行 分析。不足之处是用直接解闭环特征方程根的办法，来绘出系统的根轨 迹图，这对高阶系统将是很繁重的和不现实的。
为了解决这个问题，依据反馈系统中开环、闭环传递函数的确定关系，通过开环传递函 数直接寻找闭环根轨迹正是我们下面要研究的内容。
① (s1 p2 ) 、(s1 p3 ) 两向量对称于实轴，引起的相角大小 相等、方向相反； (s1 z2 ) 、(s1 z3 ) 两向量也对称于实轴，引起的相角大 小相等、方向相反;
∴ 判断 s1是否落在根轨迹上，共轭零、极点不考虑。
② 位于s1左边的实数零、极点：(s1 z1) 、(s1 p4) 向量引起的相
GK
(s)

kg s(s 1)
解：判断某点是否在根轨迹上，应使用相角条件。求某点对应的根轨迹增益值，应使用 幅值条件。
s1 ： m (s zi ) n (s p j ) 0 (s1 p1) (s1 p2 )
i 1
j 1
s1 (s1 1) 135 90 225
s2： 0 (s2 p1) (s2 p2) (116.6 ) (63.4 ) 180

自动控制原理 第四章 线性系统的根轨迹方法(2011-3) (2)

自动控制原理 第四章 线性系统的根轨迹方法(2011-3) (2)
要求等价为：
பைடு நூலகம்β = 45
−ξπ 1−ξ 2
β = 60
[ s]
j
⎧45° < β < 60° ⎨ ⎩ 2 < ωn < 5
−5
−2
0
13
ξ ξ ξ ξ ξ ξ ξ
= 0.0 σ % = 100% = 0.4 σ % = 25% = 0.5 σ % = 15% = 0.6 σ % = 10% = 0.7 σ % = 5% = 0.8 σ % = 2% = 1.0 σ % = 0%
A
ξ = 0.5
Im
λ3 = −2.34 X
−2
λ1 = −0.33 + j0.58
−1
X
−0.5
60
0
X
Re
λ2 = −0.33 − j0.58
21
三、高阶系统动态性能指标估算
1、高阶系统单位阶跃响应
(1) 高阶系统的单位阶跃响应包括常数项和响应模态。 (2) 除常数项以外，高阶系统的单位阶跃响应是系统模态的组 合，组合系数即部分分式系数。 (3) 模态由闭环极点确定，而部分分式系数与闭环零点、极点 分布有关，闭环零点、极点对系统动态性能均有影响。
ξ ≥ 1− r
( α)
2
ωd ≤ r
α − r ≤ ωn ≤ α + r
α − r ≤ ξωn ≤ α + r
如果设定区域
ξωn ≥ q
则选择 r ≤ min
(α − q , α
ξ ≥ ξ min
1− ξ
2 min
)
8
[例]：如图系统，求系统具有最小阻尼时K值及相应的 动态性能和稳态误差。

自动控制原理第四章习题课

自动控制原理第四章习题课

【练习】系统的闭环传递函数为)13()3(3)(23++++++=ΦK s K s s Ks s ，其中，K >0试绘制系统根轨迹，并求出s=-2时的闭环极点和零点。

解： ，得根轨迹方程：由0)13()3(323=+++++K s K s s0)1()3(13=+++s s K0)2)(2(2=+++s s s 2721,23,21js s ±-=-=⇒【练习1】一单位负反馈系统，其开环传递函数为：]4)1[()1(4)(++-=s K s s K s G(1) 试绘制K 从0→+∞时的系统根轨迹； (2) 求系统阶跃响应中含有分量)cos(βωα+-t et时的K 值范围，其中0,0>>ωα；(3) 求系统有一个闭环极点为-2时的闭环传递函数。

解：（1）根轨迹方程为：)4()2(12=+-+s s s K等效开环传递函数为：)4()2()(2+-=s s s K s G实轴上的根轨迹：[-4，0] 分离点：122411-=-=++d d d d，得：由与虚轴交点：劳斯表如下KsK s K K s 404441012-+显然，K=1时，系统处于临界稳定，由辅助方程可解出交点处21,±==ωK由模值条件得分离点处根轨迹增益：313*33*1==d K 系统根轨迹如下图所示：(２)求Ｋ值范围尼状态，分量时，系统处于欠阻当系统含有)cos(βωα+-t et系统有一对具有负实部的共轭极点，Ｋ值的范围为：131<<K(３)求闭环极点41442221=⨯⨯=-=K K s 值为：其对应的时，由模值条件，当系统具有闭环极点)445()1(]4)1[()1(4)(+-=++-=∴s s s s K s s K s G)2)(4.0()1(8.0)(1)()(++-=+=Φs s s s G s G s 闭环传递函数为：【练习2】负反馈系统的开环传递函数为22*)1)(1()2()(+-+=s s s K s G(1)绘制K 从0→+∞时的系统闭环根轨迹；(2)用根轨迹模值方程确定系统稳定 *K 的取值范围； (3)试证明复平面上的根轨迹不是圆。

自动控制原理-第四章-根轨迹法16

自动控制原理-第四章-根轨迹法16

§4.3
广义根轨迹
§4.3.1 参数根轨迹 — 除 K* 之外其他参数变化时系统的根轨迹
例2
系统开环传递函数
G(s)
(s a) 4，a=0→∞
s2 (s 1)
变化，绘制根轨迹；x1时，
F(s)?
解. (1) D(s) s3 s2 1 s 1 a 0
4
构造 “ 等效开环传递函数 ”
4 G*(s)
开环稳定 ≠ 闭环稳定
负反馈未必一定能改善系统性能
§4.4
绘制根轨迹的基本法则（20）
例3 单位反馈系统的开环传递函数为 G(s) K *(Ts 1) ，选定K*值，绘制
当T变化时的根轨迹。
s(s 1)( s 2)
D(s) s(s 1)( s 2) K *(Ts 1) 0
G*(s)
90
④ 与虚轴交点：7D(s) 4s3 s2 (14K 10)s 7(K 1) 0
ReD( j) 2 7(K 1) 0 ImD( j) 4 3 (14 10) 0
0
K 1
2
K9 7
§4.2
绘制根轨迹的基本法则（19）
例1 系统结构图如图所示
（1）绘制当K*= 0→∞ 时系统的根轨迹； （2）分析系统稳定性随K*变化的规律。 解. (2) 分析：
j)]
3
(2
20T
)
0
2.582
T 0.233
K * 20 K* 6 K* 3
自动控制原理
（第 16 讲）
§4 根轨迹法
§4.1 根轨迹法的基本概念 §4.2 绘制根轨迹的基本法则 §4.3 广义根轨迹 §4.4 利用根轨迹分析系统性能
自动控制原理
（第 16 讲）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4-1将下述特征方程化为适合于用根轨迹法进行分析的形式，写出等价的系统开环传递函数。

（1）210s cs c +++=，以c 为可变参数。

（2）3(1)(1)0s A Ts +++=，分别以A 和T 为可变参数。

（3）1()01I D P k k s k G s ss τ⎡⎤+++=⎢⎥+⎣⎦，分别以P k 、I K 、T 和τ为可变参数。

4-2设单位反馈控制系统的开环传递函数为(31)()(21)K s G s s s +=+试用解析法绘出开环增益K 从0→+∞变化时的闭环根轨迹图。

4-2已知开环零极点分布如下图所示，试概略绘出相应的闭环根轨迹图。

4-3设单位反馈控制系统的开环传递函数如下，试概略绘出相应的闭环根轨迹图（要求确定分离点坐标）。

（1）()(0.21)(0.51)KG s s s s =++（2）(1)()(21)K s G s s s +=+（3）(5)()(2)(3)K s G s s s s +=++4-4已知单位反馈控制系统的开环传递函数如下，试概略绘出相应的闭环根轨迹图（要求算出起始角）。

（1）(2)()(12)(12)K s G s s s j s j +=+++-（2）(20)()(1010)(1010)K s G s s s j s j +=+++-4-5设单位反馈控制系统开环传递函数如为*2()()(10)(20)K s z G s s s s +=++试确定闭环产生纯虚根1j ±的z 值和*K 值。

4-6已知系统的开环传递函数为*22(2)()()(49)K s G s H s s s +=++试概略绘出闭环根轨迹图。

4-7设反馈控制系统中*2()(2)(5)KG s s s s =++（1）设()1H s =，概略绘出系统根轨迹图，判断闭环系统的稳定性（2）设()12H s s =+，试判断()H s 改变后的系统稳定性，研究由于()H s 改变所产生的影响。

4-8试绘出下列多项式的根轨迹 （1）322320s s s Ks K ++++= （2）323(2)100s s K s K ++++= 4-9两控制系统如下图所示，试问：（1）两系统的根轨迹是否相同？如不同，指出不同之处。

（2）两系统的闭环传递函数是否相同？如不同，指出不同之处。

（3）两系统的阶跃响应是否相同？如不同，指出不同之处。

4-10设系统的开环传递函数为12(1)(1)()K s T s G s s++=（1）绘出10T =，K 从0→+∞变化时系统的根轨迹图。

（2）在（1）的根轨迹图上，求出满足闭环极点阻尼比0.707ξ=的K 的值。

（3）固定K 等于（2）中得到的数值，绘制1T 从0→+∞变化时的根轨迹图。

（4）从（3）的根轨迹中，求出临界阻尼的闭环极点及相应的1T 的值。

4-11系统如下图所示，试 （1）绘制0β=的根轨迹图。

（2）绘制15K =，22K =时，β从0→+∞变化时的根轨迹图。

（3）应用根轨迹的幅值条件，求（2）中闭环极点为临界阻尼时的β的值。

4-12单位正反馈系统如下图所示（1）绘制全根轨迹。

（2）求使闭环系统阻尼比0.707ξ=时的K 的取值。

4-13对于第二章例2.15的磁悬浮试验模型的例子，静态工作点附近被控对象的传递函数描述为244()1785G s s -=-（1）试确定反馈的极性和比例微分控制器(1)p k s τ+的参数，使闭环系统稳定，闭环极点的阻尼比0.707ξ=，无阻尼自然振荡频率10n ω=。

（2）试绘制0τ>、0P k >两参数变化时系统的根轨迹族。

4-12单位反馈系统如下图所示。

（1）设2a =，绘制K 从0→+∞变化时系统的根轨迹，确定系统无超调时的K 的取值，确定系统临界稳定时的K 的取值。

（2）设2K =，绘制a 从0→+∞变化时系统的根轨迹，确定系统闭环根的阻尼比0.707ξ=时的a 的取值。

4-13设单位反馈系统的开环传递函数是10(1)()(0.51)(1)s G s s Ts -=++（1）绘出T 从0→+∞变化时系统的根轨迹图。

（2）求出系统处于临界稳定和临界阻尼时的T 的值。

（3）求20T =时系统的单位阶跃响应。

4-14设系统开环传递函数如下，试画出b 从零变到无穷时的根轨迹图。

（1）20()(4)()G s s s b =++（2）30()()(10)s b G s s s +=+4-15设单位反馈控制系统的开环传递函数为*(1)()(2)K s G s s s -=+试绘出其根轨迹图，并求出使系统产生重实根和纯虚根的*K 值。

4-16设控制系统开环传递函数为*2(1)()(2)(4)K s G s s s s +=++试分别画出正反馈系统和负反馈系统的根轨迹图，并指出它们的稳定情况有何不同？ 4-17系统如下图所示（1）试绘制a T 从0→+∞变化时闭环系统的根轨迹。

（2）为使系统的阶跃响应无振荡，a T 应在什么范围内取值？ 4-18设单位反馈系统的开环传递函数为)2)(1()(++=s s s K s G（1）绘制K 从0→+∞变化时闭环系统的根轨迹。

（2）确定使闭环系统稳定的K 的取值范围。

（3）为使闭环系统的调节时间10s t =秒（按误差带5%∆=计算），求K 的取值。

解：（1）根轨迹方程为0)2)(1(1=+++s s s K ；1、 有三条分支，起始于开环极点01=p ，12-=p ，23-=p ，终止于无穷远处；2、 实轴上的根轨迹区段为：]2,(--∞，[0,1]-；3、 渐近线与实轴交点为103)2()1(0-=--+-+=aσ，夹角为(21)60,180,630a k πϕ+==--； 4、 由0)]()([=s H s G dsd 得分离点满足02632=++s s ，解为42.01-=s ，58.12-=s （舍去，因为它不在根轨迹上），1s 对应得*k 值为)2)(1(111++=*s s s k ＝0.385。

5、与虚轴的交点，将1()()0G j H j ωω+=实虚部分开有322030k ωωω⎧-+=⎪⎨-+=⎪⎩ 解出1230,01.41,61.41,6k k k ωωω***⎧==⎪==⎨⎪=-=⎩根轨迹图如下图所示。

（2）60<<K 时，闭环系统稳定。

（3）按 3.510s nt ζω==得主导极点的实部0.35n ζω-=-，系统的闭环特征方程为32123(1)(2)32()()()s s s K s s s K s s s s s s +++=+++=---式中1,2,3s 为系统的3个闭环特征根，设1,2n d s j ζωω=-±为闭环共轭主导极点，显然有123323n s s s s ζω---=-=这样得到3 2.3s =-。

根据模值条件，3 2.3s =-时的根轨迹增益33312 2.3 1.30.30.897k K s s s *==++=⨯⨯=4-19已知某单位负反馈系统的开环传递函数为2(5)()(2)K s G s s s +=+（1）绘制根轨迹简图；（2）求闭环系统出现重根时的K 值；（3）求使得闭环系统稳定且工作在欠阻尼状态的K 的取值范围。

解：（1）开环零点15z =-，开环极点10,p =232p p ==-，1m =，3n =。

系统有三条根轨迹分支，起始于极点1p 、2p 和3p ，一条终止于零点1z ，两条趋于无穷远零点。

实轴上根轨迹区域为(50-,）。

渐进线与实轴的交点为1231()0(2)(2)(5)0.531a p p p z n mσ++-+-+---===--夹角为(21)2,32a k n mπϕππ+==-在12p p 与间的实轴上存在一个分离点，分离点的坐标满足11231111d z d p d p d p =++----即2215100d d ++=得1,20.74, 6.76d =--（舍去）。

系统的特征方程为2(2)(5)0s s K s +++=，根轨迹与虚轴的交点满足2(2)(5)0j j K j ωωω+++=即2354(4)0K K j ωωωω-+-+=分别令实部和虚部等于零有2540K ω-=和340K ωωω-+=，解得16, =4.47K ω=。

根轨迹如下图。

（2）根轨迹的分离点处出现重根，根据模值条件有20.81500.81520.2740.8155K ---+==-+（3）当K 取值为(0.274, 16)时，闭环系统稳定且工作在欠阻尼状态。

4-20设单位反馈系统的开环传递函数为()(1)(1)KG s s s Ts τ=++式中2K =，1T =，0τ>为变化参数。

（1）试绘制参数τ变化时，闭环系统的根轨迹图，给出系统为稳定时τ的取值范围。

（2）求使3-成为一个闭环极点时τ的取值。

（3）τ取（2）中给出的值时，求系统其余的两个闭环极点，并据此计算系统的调节时间（按5%误差计算）和超调量。

解：（1）系统的特征方程为322(1)(1)(1)(1)220s s Ts K s s s s s s s ττττ+++=+++=++++=等效的开环传递函数为222(1)(1)()()2(0.5 1.32)(0.5 1.32)s s s s G s H s s s s j s j ττ++''==+++++-绘制根轨迹如下图。

图中根轨迹与虚轴的交点可从系统为临界稳定的条件12ττ+=得到1τ=。

1τ=时系统的特征方程为32222(2)(1)0s s s s s +++=++=得与虚轴交点的坐标为j j ω=±。

从根轨迹得到系统稳定的τ的取值范围为01τ<<。

（2）3-成为一个闭环极点时，从根轨迹的模值条件有223311(3)(3)2τ--+=-+-+得40.4449τ==。

（3）0.444τ=时，系统的另外两个闭环根从特征方程322322211299916(3)()044244s s s s s s s s s s s τττ++++=++++=+++=求出为0.125 1.218j -±，显然它是系统的主导极点。

系统的调节时间和超调量分别为 0.1251.2183.5280.125%100%100%100%100%72.5%nds t seeπξωπωσ--⨯===⨯=⨯=⨯=⨯=4-21系统如下图所示。

试绘制系统的根轨迹，并写求出当闭环共轭复数极点的阻尼比ξ=时，系统的单位阶跃响应的表达式。

0.707。